PID控制策略下主动悬架系统的动态仿真
杜常清,常晓瑞
(武汉理工大学 汽车工程学院,湖北 武汉 430070)
PID控制策略下主动悬架系统的动态仿真
杜常清,常晓瑞
(武汉理工大学 汽车工程学院,湖北 武汉 430070)
以白噪声和正弦信号作为路面激励信号,建立路面模型,再利用主动悬架的二自由度动力学模型,在Matlab/Simulink中搭建系统的仿真模型。分别在两种路面信号输入下,得到有无PID控制的主动悬架系统的仿真曲线。结合台架试验,对车身垂直加速度、悬架动挠度和轮胎动载荷进行了对比分析,证明基于PID控制器的主动悬架能够使汽车具有更好的行驶平顺性。
主动悬架;Matlab/Simulink;PID控制策略
在悬架不断改善的过程中,主动悬架的发展是大势所趋,而控制器的设计对其发展起着决定性的作用[1]。但是主动悬架系统控制复杂,在研发过程中需要基于实际工况,设计简便可行的控制策略。笔者分别在以白噪声、正弦信号为路面激励信号的基础上,搭建了有无PID控制器的主动悬架仿真模型。再结合仿真曲线和台架试验对比分析了车身垂直加速度、悬架动挠度和轮胎动载荷的变化,对改善汽车行驶平顺性具有一定的实用价值。
1 悬架系统
1.1 悬架系统概述
悬架系统包括弹簧、减震器及导向机构,其作用是传递车轮与车架之间的力及力矩,减小由于路面不平对车身的影响,从而降低振动程度[2]。主动悬架是在组成部分中增加一个可控执行器,从而主动调整车身的运行状态,其性能差别主要体现在行驶平顺性上。而行驶平顺性的改善与车身垂直加速度息息相关,对加速度的控制是使车身尽可能保持平稳的关键。
1.2 悬架系统的评价指标
1.2.1 车身垂直加速度
据资料显示,人体对4~8 Hz的振动最为敏锐,车身垂直加速度很大程度上决定了汽车的行驶平顺性[3]。
1.2.2 悬架动挠度
当运动空间一定的时候,过大的悬架动挠度会使车辆行进过程撞到限位块的概率提高,影响其平顺性[4]。
1.2.3 轮胎动载荷
轮胎的动载荷与轮胎变形量、弹性刚度系数正相关。
2 主动悬架系统模型
2.1 二自由度主动悬架的动力学模型
为方便研究,让过程简单明朗化,笔者将模型简化,得到二自由度的1/4主动悬架模型,如图1所示。假定轮胎不离开地面,xs、xt分别表示悬架和车轮偏离静平衡点的距离,参数定义见表1。
基于牛顿第二定律得到该模型的动力学方程为:

图1 二自由度的1/4主动悬架模型

表1 参数定义
kt(xt-xr)+u=0
(2)
利用式(1)和式(2)在Matlab/Simulink中搭建二自由度主动悬架系统的仿真模型,如图2所示。

图2 二自由度主动悬架仿真模型图
2.2 路面路谱模型建立
建立路面扰动激励模型是进行研究工作的基础。以GB7031-865《车辆振动输入-路面不平度》为依据,路面位移功率谱密度Gq(n)为[5]:
Gq(n)=G0(n0)(n/n0)-w
(3)
式中:n为空间频率;G0(n)为路面不平度系数;w为频率指数。
(4)
式中:xr(t)为路面垂直位移激励;w(t)为高斯分布白噪声。
根据统计,我国路面中B、C级路面所占比例较大,笔者以B级路面为例,设置车速为20 m/s,n0=0.1m-1,Gq(n0)=64×10-6m2/m-1。利用式(4)在Matlab/Simulink中搭建B级路面谱的仿真模型,分别如图3~图5所示。其中,图5是将白噪声改为正弦信号作为输入模型。

图3 路面谱的仿真模型

图4 积分白噪声路面输入模型
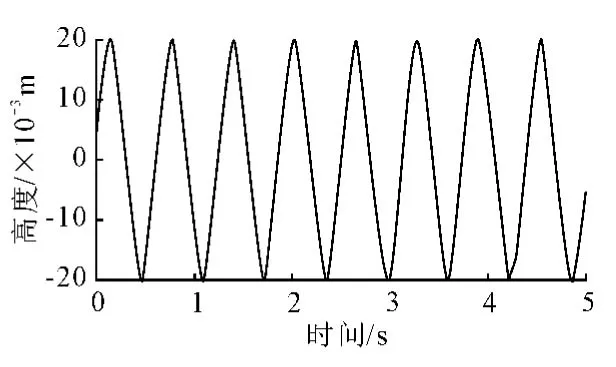
图5 正弦信号路面输入模型
3 基于1/4悬架系统模型的PID控制
3.1 PID控制
常见的PID控制系统主要包含PID控制器和所控对象,其原理框图如图6所示。在设定值r(t)与实际输出值y(t)之间存在控制偏差e(t),线性组合后得到控制量u(t)对目标进行控制。
(5)
式中:e(t)=r(t)-y(t);KP为比例系数;TI为积分时间常数;TD为微分时间常数。
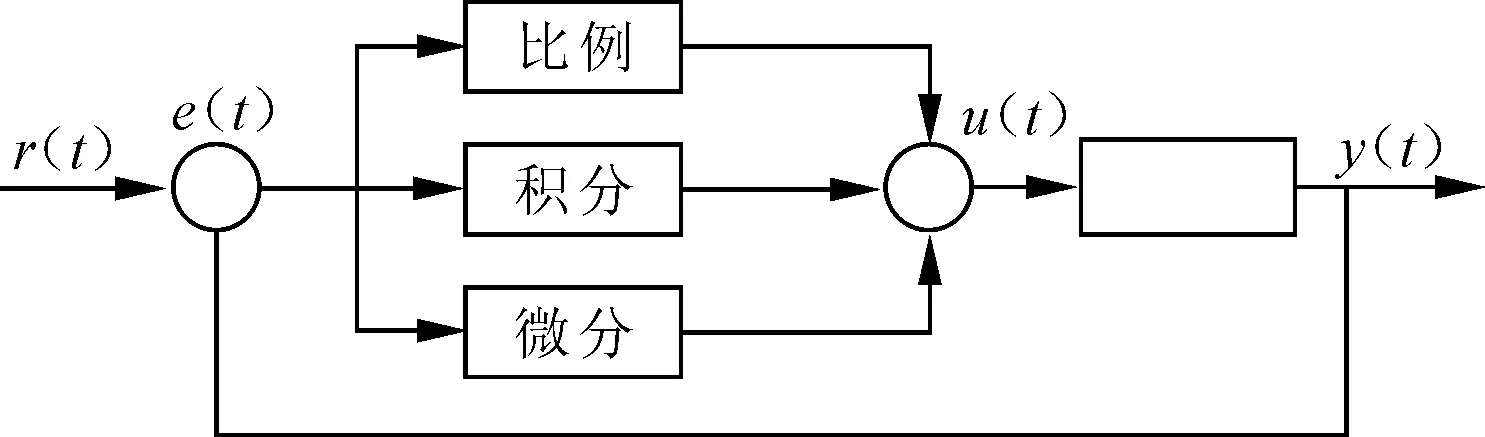
图6 PID控制系统原理

(6)
根据式(5)~式(6),在Matlab/Simulink中搭建PID控制器的仿真模型[8],如图7所示。
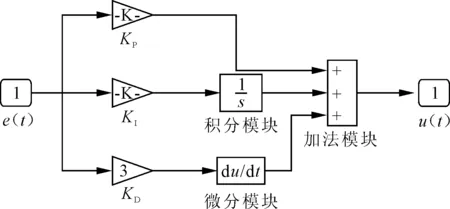
图7 PID控制模型
3.2 主动悬架系统的PID控制
在Matlab/Simulink中结合路面激励、二自由度主动悬架和PID控制器仿真模型搭建有无PID控制的主动悬架仿真模型,如图8所示。
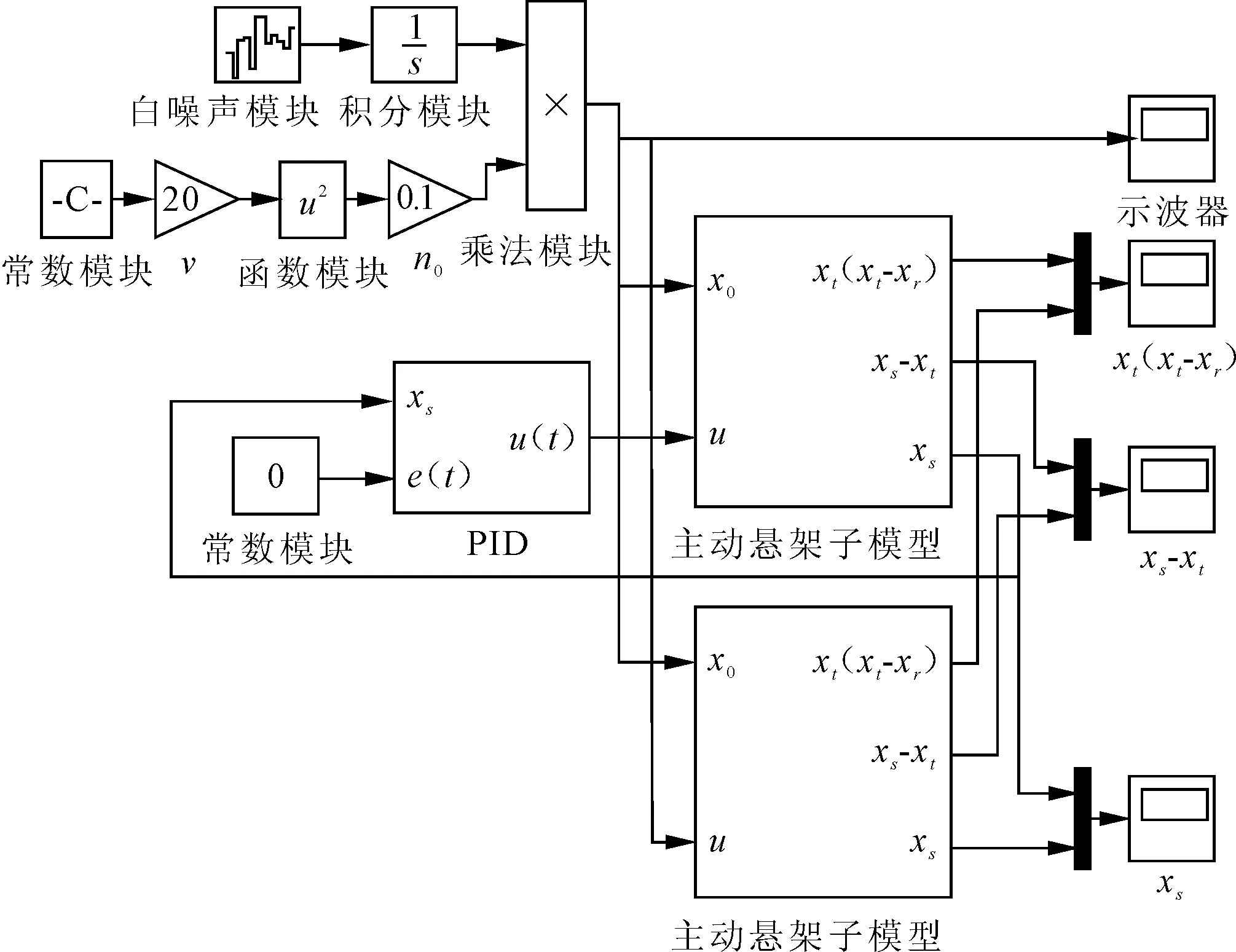
图8 主动悬架仿真模型
3.3 PID控制器的参数确定
调整PID控制模型中的KP、KI、KD这3个参数使其达到最佳值,即对其进行整定,使其控制达到预定要求。笔者运用试凑方法选定KP、KI、KD这3个参数的3处最佳值。整定步骤参照经验公式及主动悬架的特性按比例-积分-微分确定[9]。在多次运行仿真后得到最佳参数分别为:KP=120,KI=3 000,KD=3。
4 悬架系统仿真实验及结果分析
4.1 仿真参数
依据图8中的仿真模型,在白噪声、正弦信号两种不同路面激励信号下,在Matlab/Simulink中,分别对有无PID控制的主动悬架进行仿真,时间定为5s。仿真过程中所选取的模型参数如表2所示。

表2 模型参数
4.2 仿真结果对比分析
4.2.1 白噪声信号下的比较
白噪声信号下,对有无PID控制器的主动悬架进行仿真,得到车身垂直加速度、悬架动挠度和轮胎动载荷3个评价指标的仿真曲线,分别如图9~图11所示。

图9 白噪声信号下车身垂直加速度仿真曲线

图10 白噪声信号下悬架动挠度仿真曲线
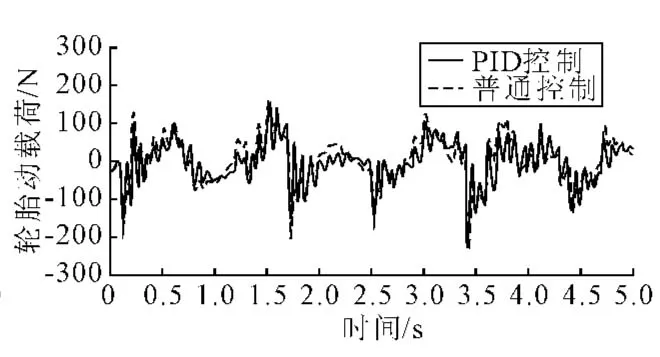
图11 白噪声信号下轮胎动载荷仿真曲线
由图9~图11的曲线对比可以看出,在白噪声信号下,PID控制主动悬架的车身垂直加速度约在-0.4~0.4 m/s2之间变化,明显优于无PID控制器主动悬架的-0.5~0.6 m/s2;PID控制主动悬架动挠度控制在-0.006~0.005 m,优于无PID控制器主动悬架的-0.006~0.007 m;两者轮胎动载荷峰值虽相差不大,但从整体曲线上来看,PID控制的主动悬架效果较优。
4.2.2 正弦信号下的比较
将路面激励由白噪声改为正弦信号输入,得到车身垂直加速度、悬架动挠度和轮胎动载荷这3项指标的仿真曲线,分别如图12~图14所示。
从图12~图14可以看出,在正弦信号下,有PID控制器的主动悬架系统相较无PID的系统而言,3项评价指标车身垂直加速度、悬架动挠度和轮胎动载荷都有所改善。车身垂直加速度从-2.5~2.5 m/s2降到了-1.8~1.8 m/s2;悬架动挠度从-0.035~0.035 m降到了-0.03~0.03 m;轮胎动载荷从-800~800 N降到了-450~450 N。
4.3 实验对比
通过悬架台架试验测得主动悬架在有无PID控制器时各个参数值,通过对车身垂直加速度各个测量值进行加权平方根的计算,得到的对比结果如表3所示。从表3可以看出,PID控制器对主动悬架起到优化作用,在车身垂直加速度加权平方根、悬架动挠度和轮胎动载荷系数均有所改善,达到了提高平顺性的效果。

图12 正弦信号下车身垂直加速度仿真曲线

图13 正弦信号下悬架动挠度仿真曲线

图14 正弦信号下轮胎动载荷仿真曲线

表3 有无PID控制的主动悬架性能对比
5 结论
分别以白噪声和正弦信号作为路面激励信号,使用PID控制的主动悬架系统,无论从仿真曲线还是从台架试验结果来看,悬架系统3项评价指标相对于无PID控制主动悬架来说,均得到了良好的改善。悬架动挠度的降低使得其利用工作空间得到了更为充分的应用。此外,在轮胎动载荷基本相同的情况下,PID控制的主动悬架显著降低了车身垂直加速度,对改善汽车行驶平顺性具有一定的参考价值。
[1] 马宝山.汽车悬架振动主动控制技术研究[D].哈尔滨:哈尔滨工程大学,2003.
[2] 夏爽.基于四分之一悬架模型与整车虚拟样机的主动悬架控制系统仿真研究[D].沈阳:东北大学,2008.
[3] 丁建超.提高工程车辆舒适性技术研究[D].北京:北京建筑工程学院,2008.
[4] 高益财.基于DSP的半主动悬架模糊控制器的研究与开发[D].成都:西华大学,2007.
[5] 鞠成超.重型商用车行驶平顺性分析与优化[D].长沙:湖南大学,2009.
[6] 江帅.煤矿井下无轨胶轮车油气悬架动态特性仿真与优化[D].太原:太原理工大学,2010.
[7] 孟祥光.基于虚拟样机主动悬架仿真控制研究[D].西安:长安大学,2011.
[8] HROVAT D. Optimal active suspension structures for quarter car vehicle models [J].Automatic,1990(26): 845-860.
[9] 李建新,李跃新.PID控制算法专家参数自整定的研究[J].新技术新工艺,2007(10):44-47
DU Changqing:Assoc. Prof. ; School of Automotive Engineering, WUT, Wuhan 430070, China.
[编辑:王志全]
Dynamic Simulation of Active Suspension System Based on PID Control Strategy
DUChangqing,CHANGXiaorui
The road model was established white noise and sine signal were taken as the road excitation signal. Two dynamic models of active suspension were utilized in creating the system simulation via Matlab/Simulink. Taking the two signals as input respectively, the simulation curves of active suspension system with and without PID controller were obtained. Then the curves were compared with each other. The body vertical acceleration, suspension dynamic deflection and tire dynamic load were compared and analyzed. It proves that the active suspension system based on PID controller increases the ride comfort of vehicles.
active suspension; Matlab/Simulink; PID control category
2015-06-22.
杜常清(1975-),男,四川南充人,武汉理工大学汽车工程学院副教授;博士.
中央高校基本科研业务费专项资金资助项目(2015Ⅲ002).
2095-3852(2015)06-0680-04
A
U391.9
10.3963/j.issn.2095-3852.2015.06.004

