一种基于有向图的多维多值属性关联规则挖掘算法

汪峰坤，张婷婷

安徽机电职业技术学院，安徽芜湖，241000



一种基于有向图的多维多值属性关联规则挖掘算法

汪峰坤，张婷婷

安徽机电职业技术学院，安徽芜湖，241000

针对多维多值数据特点，提出了基于FP-Growth的改进算法FP-G。FP-G算法存储结构使用有向图，增加了头结点，方便对图剪枝和遍历。针对图结构使用了新的剪枝策略，对于小于最小支持度的边直接删除，无须修改结点指针。关联规则生成时通过头结点进行深度遍历生成最大频繁模式集。实验结果表明，FP-G算法相比FP-Growth算法，在百万数量级的高维数据集上，执行时间平均节约30%左右。

数据挖掘；关联规则；频繁项集；多值属性

1 问题的提出

关联规则数据挖掘是从海量数据中发现数据集之间潜在联系的一项技术。根据数据集维数是否大于1，数据挖掘分为单维和多维两种；又根据数据集属性取值情况，分为布尔和多值两种情况。

Srikant R.和Agrawal R.于1996年提出了基于Apriori算法的多值属性关联规则[1]，即通过量化规则将数据集的属性转换为单维二元属性，然后使用经典的Apriori算法进行挖掘，但容易造成事务属性急剧增加，挖掘效率较低。后来，国内学者穆云婷等提出了基于FP-Growth的多维关联规则挖掘[2]即把树中每个节点作为一个属性值，树中每个分支作为数据集中的一条记录，在第一次扫描数据库时统计1阶频繁集，按个数的逆序生成头节点列表。第二次扫描数据库时生成频繁树，树中每个节点出现下一属性指针等，但当维数和属性值较多时生成的树的深度很大，生成关联规则较慢。

在多值属性挖掘应用中，在某些情况下一条记录中某属性的取值是唯一的。例如，某位教职工在某次常规体检中，他的空腹血糖只能是正常、受损、糖尿病三种情况中的任意一种，不可能同时是两种及两种以上的组合。针对这些情况的应用，本文提出了FP-G算法。FP-G算法是FP-Growth关联规则的一种改进算法，它通过修改FP-Tree为有向图、增加新的数据存储结构和优化的剪枝策略，提高了算法执行的效率，实验结果验证了它的有效性。

2 关联规则的基本概念和理论

关联规则挖掘中基本概念和相关定义[1-8]：

定义1 设I={I1，I2，…，Im}是文字属性，称为项(item)。给定一个事务数据库D，其中每个事务T是项的集合，满足T⊆I。每个事务都有一个标识符，称为TID。X是I的子集，如果X⊆I，则称T包含X；如果X的元素个数为k，则可以称X为k-项集(k-ItemSet)。

定义2 如果项集X⊆I，Y⊆I，并且X∩Y=∅，形如X⟹Y的蕴涵式称为关联规则，其中，X称为规则的前项集，Y是规则的后项集。

定义3 给定最小支持度阈值minSup，如果项集X的支持度大于等于minSup，则称X为频繁项集。频繁k项集的集合记为项集Lk。

对于数据挖掘中的关联规则主要有两个步骤：(1)给定事务数据库D和项目集I={I1，I2，…，Im}，发现D中所有大于指定minSup的频繁模式完全集P；(2)从频繁项集中的每个频繁模式中抽取关联规则I⟹l-s，其置信度大于等于minConf。其中，第(1)步是核心，决定挖掘关联规则的总体性能。

关联规则挖掘算法中的主要性质：

性质1 频繁项集的所有非空子集都是频繁的。

性质2 非频繁项集的所有超集都是非频繁项集。

在多维多值属性挖掘应用中，有些应用针对某个属性在一条记录中其取值是唯一的，有如下性质：

性质3 每条事务所包含的属性数目相同，即每个事务的长度相同。

性质4 某一属性的不同的属性值不会出现在同一个频繁属性集中。

3 改进算法

3.1 算法的基本数据结构

设事务数据有N维，每一维的属性都是多值属性，各维属性个数为：x1,x2,…，xn。设第m维的属性取值标记为Vm(1),Vm(2),…，Vm(xm)。

构建基于维的单链表，每个单链表对于某一维的所有属性取值。

单键表中每个节点包括3个数据域和2个指针域。

属性值：指此节点所在维属性取值的一个。

出现次数：指此节点在数据库中出现的次数。

next指针：指向下一维的某个节点，表示此节点值和下一节点值在某条事务中同时出现。

next指针个数：表示此节点值和下一节点值在事务数据库中一共出现了多少次。

right指针：指向同一维的下一个属性值节点。

3.2 FP-G算法流程

3.2.1 构建有向图G

(1)第一遍扫描事务数据库D，统计每一维的每个属性值出现的个数，生成一阶频繁子集。

(2)根据一阶频繁子集和频繁项所在的维，按顺序生成相应的单链表，每一维生成一条单链表。每条单链表中每个节点是此维的频繁属性值。

(3)生成G的Head节点，Head节点通过指针指向第一维的所有节点。

(4)第二遍扫描事务数据库D，对于每条记录按维加入到FP-G中。首先去除不在一阶频繁子集中的维，然后根据记录中各维值的顺序关系在FP-Tree中增加边。如果是第一次增加，将节点的next指针指向下一维值对应的节点。如果不是第一次增加，将next个数加1，并且将两个节点出现次数加1。

3.2.2 生成关联规则

(1)深度遍历有向图G，将边值小于minSup的边删除。如果剩余路径上的结点还有父指针指向，则不作处理；如果没有父指针指向，则挂在Head节点下。当遍历结束时，树中结点之间的边数目都是大于minSup的。

(2)再深度遍历有向图G，得到的每条路径就是满足minSup的最大频繁模式项。

(3)最后根据组合算法，可求出所有频繁项。

本算法类似于FP-Growth算法，都是在内存中生成事务数据库的结构。根据多维多属性数据特点，使用的是有向图作为内存数据存储结构。在根据有向图生成关联规则之前，对有向图G使用了新的剪枝策略。生成关联规则时，先生成最大频繁模式集，最后根据最大频繁模式集生成所有的频繁集。

4 FP-G算法实验与分析

4.1 算法流程实验

某事务数据库中有6个事务，D={T1,T2,T3，T4,T5,T6}，每条事务固定有4个属性，每个属性有若干取值。如表1所示。

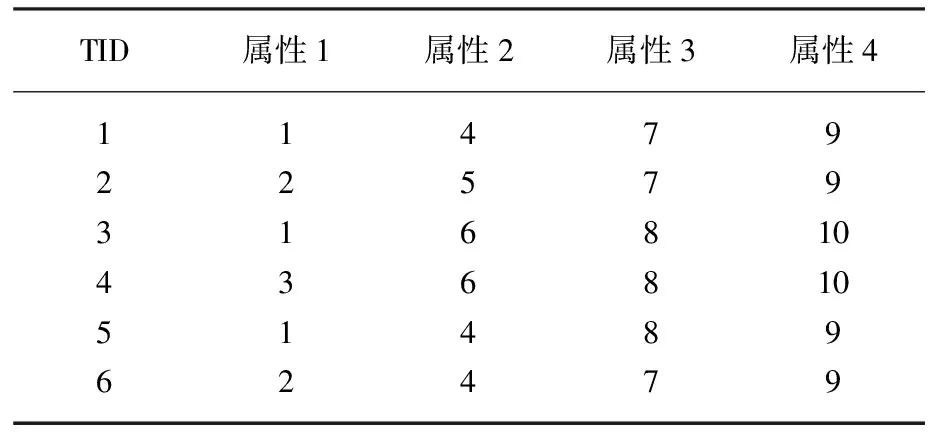
表1 多值属性数据示例

假设最小支持度30%，即最小支持计数为：minSup=30%×|D|=30%×6≈2。

图1 生成的FP-G图

(1)第一遍扫描事务数据库D，统计每一维的属性值出现的个数。统计结果：{{"1"∶3,"2"∶2,"3"∶1},{"4"∶3,"5"∶1,"6"∶2},{"7"∶3,"8"∶3},{"9"∶3,"10"∶2}}。根据minSupNum=2，则得到一阶频繁子集：{{"1"∶3,"2"∶2},{"4"∶3,"6"∶2},{"7"∶3,"8"∶3},{"9"∶4,"10"∶2}}，并同时生成一阶频繁子集相应维的单链表和Head节点。

(2)第二次扫描事务数据库，将记录按维加入到FP-G中。规则是，每条记录按维在图G上生成边。如果维值不在图中，则跳过此维。如果两维之间的边不存在，则增加边并计数为1。如果两维之间的边存在，则边上的计数加1。

本例中，生成的FP-G如图1。

(3)对FP-G进行遍历剪枝。深度遍历图G，去除边计数小于minSupNum的边(与Head相连的除外)。结果如图2所示。

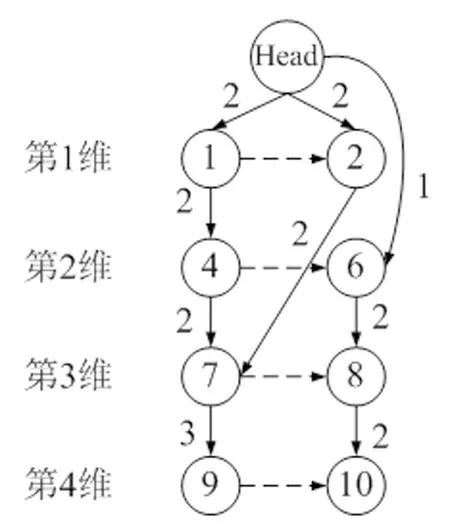
图2 剪枝后的FP-G图

(4)深度优先遍历FP-G，得到满足minSup的最大频繁模式集：{{"1"∶2,"4"∶2,"7"∶3，"9"∶null},{"2"∶2,"7"∶3,"9"∶null},{"6"∶2,"8"∶2,"10"∶null}}。数据含义：“1”等是指某维的属性值节点，属性值后面的数字指此节点与下一节点的连接边的个数。根据组合算法，可以得到所有的频繁项。

4.2 算法性能比较

关联规则挖掘中，核心内容是生成支持minSup的频繁模式完全集，决定了算法的总体性能。本文以生成频繁模式完全集的时间开销，来对FP-G算法和FP-Growth算法进行性能比较。

测试数据为某医院健康体检数据，共有9个属性，即9维，每个属性有3～5个属性值。取最小支持度为10%，数据量从16万条升到200万条。

图3 低维数据运行时间和数据量关系

由图3中可见，当数据量较少时，FP-G算法性能与FP-Growth算法性能相近。在数据量较大时，FP-G算法要优于基本的FP-Growth算法。

图4为数据集有16维，每维有3～5个属性值时的性能比较。

从图4中可见，FP-Growth对维数敏感，当数据集的维数较高时，算法开销比较大。FP-G算法在高维数据集上算法性能也较好。

图4 高维数据运行时间和数据量关系

图5表示FP-G算法在不同的最小支持度下的性能，测试数据集共16维，每维3～5个属性值，数据集有100万条记录。

图5 FP-G运行时间和最小支持度关系

从图5中可见，当最小支持度过小时，需要更长的运行时间，因为要判断和生成图中更多的边。当最小支持度较大时，运行时间较短，最后稳定在某个时间值，这个时间值应该是扫描两次数据集所用的时间。选择合适的最小支持度，FP-G算法在较大数据集上性能表示良好。

5 结束语

本文根据多维多值关联规则的特点，提出了基于有向图的关联规则挖掘算法。该算法总体思路类似于FP-Growth算法，通过第一遍扫描数据库计算一阶的频繁集，通过第二遍扫描数据库在内存中生成基于有向图的频繁数据结构。相对于FP-Growth算法，该算法无须对一阶频繁集排序，也无须生成每个叶子结点的指向下一个相同结点的指针。结合本文提出的剪枝策略，可以方便地生成最大关联规则模式集。通过仿真，本算法性能相对于经典的FP-Growth算法有了一定的提升。

[1]AgrawalR,ImielinskiT,SwamiA.MiningAssociationRulesBetweenSetsofItemsinLargeDatabases[J].ACMSIGMODRecord,1993,22(2):207-216

[2]穆云婷,谢文阁.基于FP-Growth算法的多维关联规则挖掘方法[J].辽宁工业大学学报：自然科学版,2010,4(2):81-83

[3]杨云,罗艳霞.FP-Growth算法的改进[J].计算机工程与设计,2010,31(7):1506-1510

[4]姜丽莉,孟凡荣,周勇,等.多值属性关联规则挖掘的Q-Apriori算法[J].计算机工程,2011,37(9):81-83

[5]郑亚军,胡学钢.基于PFP的关联规则增量更新算法[J].合肥工业大学学报,2015,38(4):500-505

[6]石杰.一种快速频繁模式挖掘算法[J].烟台大学学报：自然与工程版,2015,28(2):113-119

[7]Sathish K.Efficient tree based distributed data mining algorithms for mining frequent patterns[J].International Journal of Computer Application,2010,11(10):233-242

[8]Rahul M.Comparative analysis of apriori algorithm and frequent pattern algorithm for frequent pattern mining in web log data[J].International Journal of Computer Science and Information Technologies,2012,3(4):4662-4665

(责任编辑：汪材印)

2015-06-29

安徽省高校省级自然科学研究重点项目“基于移动客户端的教职工健康体检数据智能分析管理系统的研发”(KJ2014A038)。

汪峰坤(1978-)，安徽霍邱人，硕士，讲师，主要研究方向：数据挖掘、大数据处理。

TP301.6

：A

：1673-2006(2015)12-0099-04

10.3969/j.issn.1673-2006.2015.12.027