快速计算N2、空气和CO2在地面和储层条件下压缩因子
中原石油工程设计有限公司
快速计算N2、空气和CO2在地面和储层条件下压缩因子
何佳中原石油工程设计有限公司
气驱应用过程中,在注入气体积计算、泡沫驱中的泡沫密度计算及储层条件下气体PVT相态计算中,都需要对储层条件下气体的密度进行较为精确的计算。目前气体的热力学性质计算方法可分为图表法、状态方程法和拟合关联式法三类。由于采用拟合关联式法建立压缩因子的快速计算模型需要充足的压缩因子参考,而采用双自变量拟合方程,通过选取合适的n值,对N2、空气和CO2气体的压缩因子进行拟合计算,可取得较好的计算精度,该拟合方程可以直接应用于CO2溶解度模型中。
气驱;压缩因子;拟合方程;计算模型
气驱应用过程中,在注入气体积计算、泡沫驱中的泡沫密度计算及储层条件下气体PVT相态计算中,都需要对储层条件下气体的密度进行较为精确的计算。目前气体的热力学性质计算方法可分为图表法、状态方程法和拟合关联式法三类。前两类方法具有各自的优点,但一个显著的缺点是现场应用较为不便。而上述三种气体在地面和储层条件下压缩因子的快速计算方法(尤其是计算精度高、易于进行数学运算的快速计算方法,如微积分运算),目前国内报道较少。
采用盛景云等提出的双自变量化学化工实验数据的拟合方程,并根据不同气体特点选用合适的区间,针对实验数据进行拟合,得到N2、空气和CO2气压缩因子的快速计算方法。
1 拟合方程
1.1拟合方程的提出
假设y是以x和t为自变量的函数,y=f(x,t),对x(设其取值范围为x0~xn)进行归零归一和一般幂函数变换,即令

式中a为参数。在拟合数据时,可改变a值使评价相对误差(ARD)最小。
在第二自变量t和参数a固定的情况下,由实验数据组(xi,yi)可得变换后的数据组(ui,yi),此数据组组成一条曲线,将此曲线划分为n个区间。在实际应用中,一般取n为1或2即可满足要求。例如,当n=3时,u0=1,u3=1,即
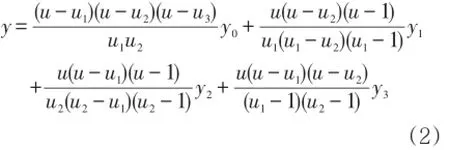
y1由已知实验数据点组成,所以拟合误差较小,yi可用式(2)或非整数次幂多项式表示
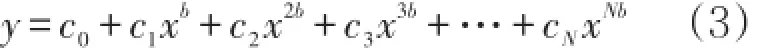
式中b、y0、y1、y2为新方程参数;ci为普遍多项式待定系数。
1.2各气体拟合方程中n的选取
由于n的选取其物理意义是将数据组(ui,yi)组成的曲线划分成n个区间。因此,n越大,对数据拟合的结果越精确,但是会增加需要拟合的参数。本文结合N2和空气更接近于理想气体,其拟合方程中的n选为2,而CO2由于在超临界区域压缩因子变化较大,因此选取n为3。
由于采用拟合关联式法建立压缩因子的快速计算模型,需要充足的压缩因子参考数据,而文献中报道的实验数据较少,用其进行拟合得到的参数,虽能在实验点处取得较好的计算精度,但内插计算往往会产生较大误差。N2和空气压缩因子采用REFPROP7中导出的数据作为快速计算模型的原始数据。REFPROP是参考流体物性的缩写,是由美国国家标准计量局开发的,用于为工业中重要的流体及混合物的热力性质和传输特性提供数据和图表。
2 计算结果
2.1N2压缩因子拟合
根据油田气驱现场和储层的条件,选取N2的温度范围为273.15~423.15K,压力范围为0.1~30MPa。采用遗传算法,拟合结果见表1。相关系数(R)为0.998,相对平均偏差为0.23%。N2压缩因子拟合实验值与计算值对比见图1。
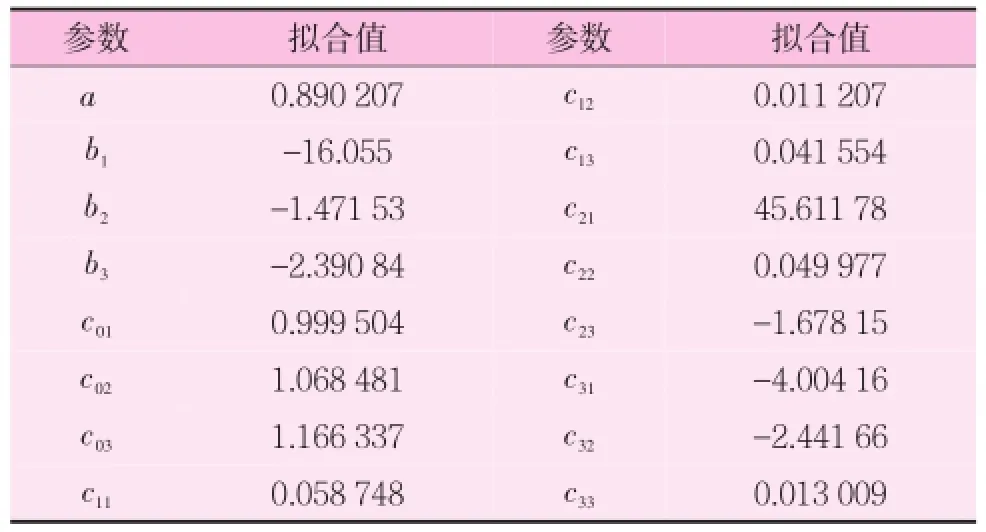
表1 N2压缩因子拟合参数
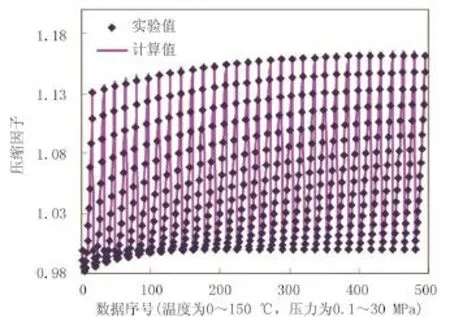
图1 N2压缩因子拟合实验值与计算值对比
2.2空气压缩因子拟合
根据油田气驱现场和储层的条件,选取空气的温度范围为273.15~423.15K,压力范围为0.1~30MPa。采用遗传算法,拟合结果见表2。相关系数(R)为0.998,相对平均偏差为0.13%。空气压缩因子拟合实验值与计算值对比见图2。
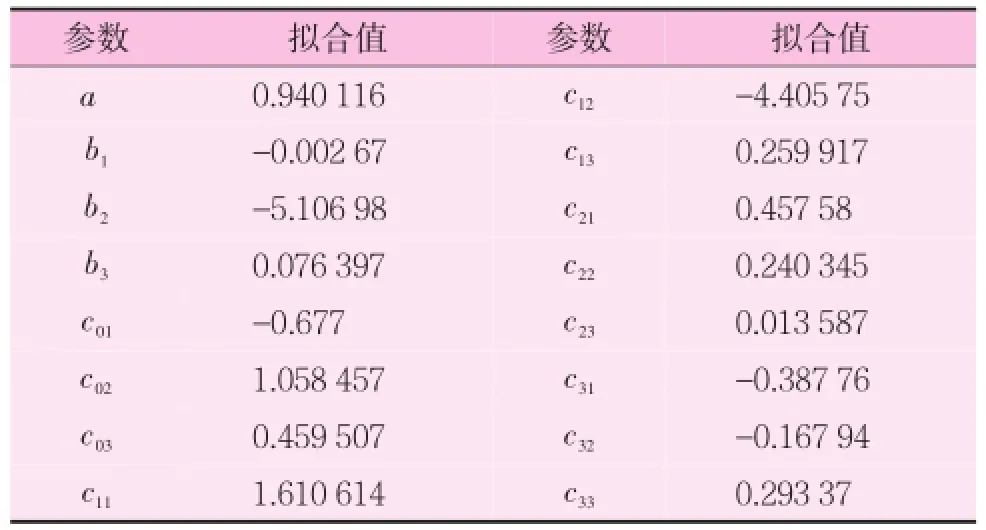
表2 空气压缩因子拟合参数
2.3CO2压缩因子拟合
根据油田气驱现场和储层的条件,CO2压缩因子在超临界区变化较大,难于计算精确。因此,部分选择对超临界CO2的压缩因子进行拟合。选取CO2的温度范围为310~550K,压力范围为7.5~60.5MPa。采用麦夸特法,拟合结果见表3。相关系数(R)为0.9958,相对平均偏差为1.53%。本文CO2压缩因子采用文献报道值,如表3所示。CO2压缩因子拟合实验值与计算值对比见图3。
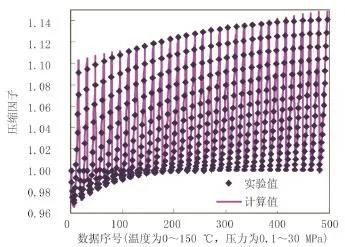
图2 空气压缩因子拟合实验值与计算值对比
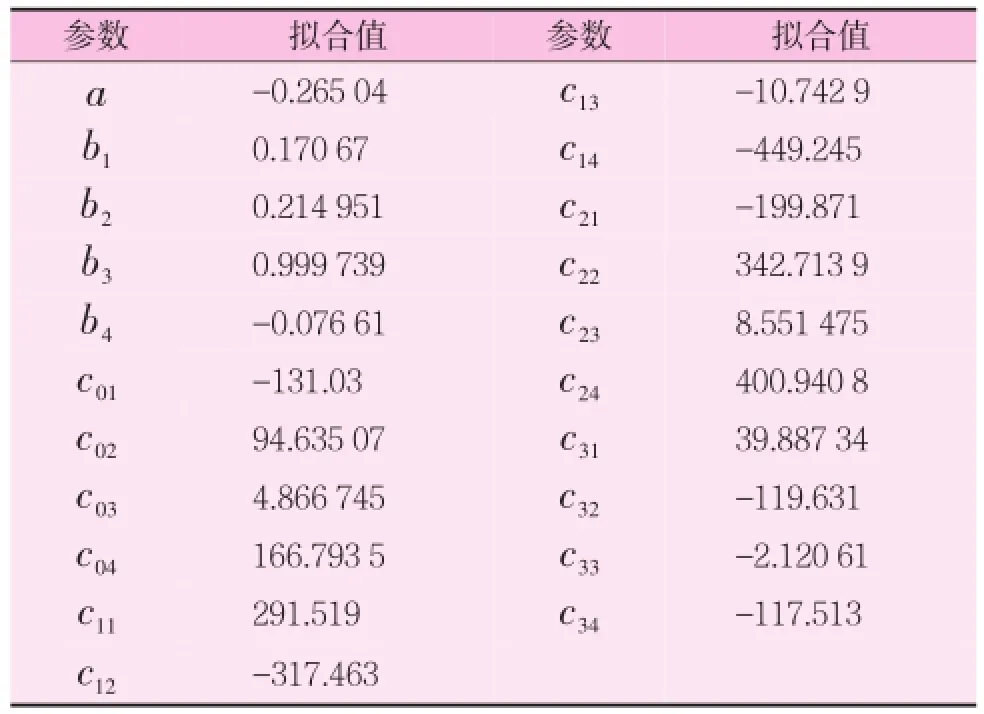
表3 CO2压缩因子拟合参数
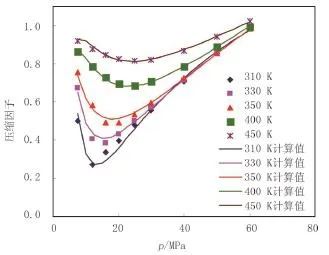
图3 CO2压缩因子拟合实验值与计算值对比
3 结语
采用双自变量拟合方程,通过选取合适的n值,对N2、空气和CO2气体的压缩因子进行拟合计算,拟合方程取得了较好的计算精度,该拟合方程可以直接应用于CO2溶解度模型中。
(栏目主持杨军)
10.3969/j.issn.1006-6896.2015.2.003
——北美又一种非常规储层类型

