为什么要引入溶剂的渗透因子*
刘国杰 黑恩成
(华东理工大学化学系 上海200237)
在溶剂A中加入溶质B而变成二元溶液时,由于组分间的相互作用,系统会偏离理想状态。然而,它们的化学势改变却严格地遵守Gibbs-Duhem方程:

式中μi=+RTlnγixi,dμi=RTdlnγi+RTdlnxi。式(1)也可表示为:

由于xAdlnxA+xBdlnxB=dxA+dxB=0,故式(2)可表示为:

或者为:

25℃时,在质量摩尔浓度b=2 mol/kg的KCl水溶液中,溶质KCl的物质的量分数xB=0.0672,溶剂水的物质的量分数xA=0.9328,实验测得KCl的平均离子活度因子γ±=0.614,水的活度因子γA=1.004 。可见,溶质的γ±变得明显小于1,而溶剂的活度因子几乎没有改变。
由热力学可知,活度因子γi是作为组分i偏离理想状态的程度而引入的。上述例子表明,对于电解质稀溶液中的溶剂,γA并不是一个表征其非理想性的满意指标。Bjerrum为此引入了一个溶剂的渗透因子,便是为了增加稀溶液中溶剂非理想性的灵敏度。
1 渗透压与渗透因子
何谓渗透因子?这个问题可从溶液的渗透压[2]谈起。
有一容器,如图1所示,其中虚线AB为半透膜,只允许溶剂分子通过,而不允许溶质分子通过。在开始时,若膜的两侧都是纯溶剂,温度为T,压力为p0,则平衡时α侧和β侧的液面高度相同。
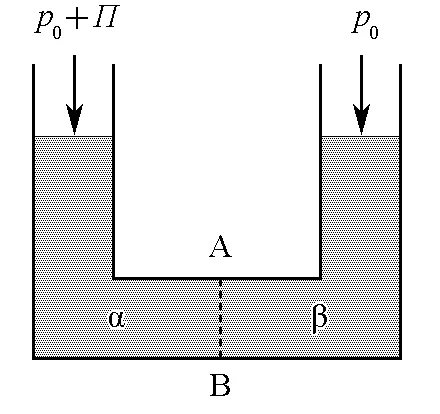
图1 渗透压示意图
若在α侧加入溶质,则因半透膜不允许溶质分子通过,β侧始终是纯溶剂,且温度和压力依然是T和p0,因此,β侧溶剂的化学势保持不变。但因α侧加入了溶质,溶剂的化学势就会降低,这便使溶剂从β侧通过半透膜渗入α侧。为了防止渗透,必须提高α侧的压力,以补偿因加入溶质所引起的溶剂化学势降低。增加的压力Π即为相应浓度下的渗透压,因此,α侧溶剂化学势的微变当为:

或者为:

将等式两边积分,则有:

因α侧为纯溶剂(xA=1)时,压力为p0,加入溶质变为浓度xA的溶液时,压力增至p0+Π,这便决定了式(7)的积分上下限。式中VA为指定温度、压力和浓度下溶剂的偏摩尔体积。
由于溶剂的化学势μA=μ*A+RTlnaA,式(7)等号左边积分为:

注意到当式(8)中xA=1时,aA=1,lnaA=0。且严格地说,式中的aA是指压力为p0时的值。
式(7)等号右边积分为:

这里,假定渗透压Π不大,以致溶剂在指定温度和浓度下的偏摩尔体积可视为常数。将式(8)和式(9)代入式(7),遂得:

式(10)就是渗透压与溶剂活度的关系式。
如果将式(10)中的lnaA表示成如下形式也未尝不可:

则式(10)变为:

此时g成了渗透压公式中的一个因子,故称为合理渗透因子。
2 合理渗透因子
在溶液很稀时,因

将式(13)代入式(12),可得:

式中nAVA≈V,cB=nB/V。由于理想稀溶液的渗透压Πid=cBRT,故合理渗透因子为:

即其值等于电解质溶液的实际渗透压与理想稀溶液的渗透压之比[3],这就是合理渗透因子的物理意义。
由式(11)可见,合理渗透因子是较为严格的,只要渗透压不是很大,它可适用于各种浓度的溶剂。若将式(11)与μA=+RTlnaA相结合,可得:

式(16)便是合理渗透因子的定义式。
由式(11)还能得到:

式(17)即是溶剂的合理渗透因子与活度因子的关系式。
按照式(17),可以算得上述KCl水溶液中水的合理渗透因子为:

其值显著地比1小。
不难证明,如果用g来取代γA,其灵敏度将显著地提高。因为由式(17)可得:

将式(19)代入Gibbs-Duhem方程(式(3)),则得:

对于稀溶液,由式(13)知lnxA≈-xB,故有:

式(22)也可表示为:

由于在稀溶液中,xAg的值小于1,故它的灵敏度dg/g不比γB的灵敏度小。
3 实用渗透因子
前面已述,Bjerrum引入渗透因子的目的是要在稀溶液时增加溶剂非理想性的灵敏度,故若从稀溶液的角度来定义渗透因子,可能会更加灵敏,这便出现了另一种渗透因子。
已知在电解质稀溶液中,xA与质量摩尔浓度b间有如下关系:

式中MA为溶剂的摩尔质量,ν=ν++ν-为一个电解质分子解离生成的正、负离子总数。故在稀溶液时,有:

由于稀溶液中溶剂的化学势为:

据此,可以定义一个新的渗透因子[4]:

这个渗透因子φ称为实用渗透因子。
将式(27)与μA=+RTlnaA相结合,可得:

式(28)则是实用渗透因子与活度因子的关系式。不难看出,仅当电解质溶液无限稀释时,式(28)才变成式(17),此时,两种渗透因子的数值相等。
按照式(28),可以算得上述KCl水溶液中水的实用渗透因子为:
可见,φ比g更小。
不难证明,若采用实用渗透因子,则由式(28)可得:

将式(30)代入式(3),得:
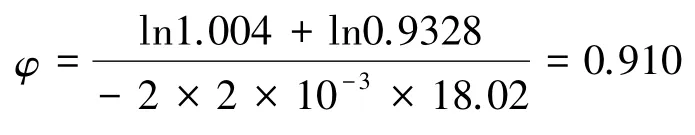
式中代入了式(24)。
当溶液较稀时,xB≪xA,式(32)也可表示为:

比较式(23)与式(33),可得:

由于φ<g,所以φ的灵敏度比g的灵敏度更高,这就是实用上更多采用φ的原因。
4 两种渗透因子的换算
两种渗透因子间的关系可由它们的定义式得到。由式(16)和式(27)可得:

由于按照式(24),-lnxA可级数展开成:

将它代入式(36),遂得:
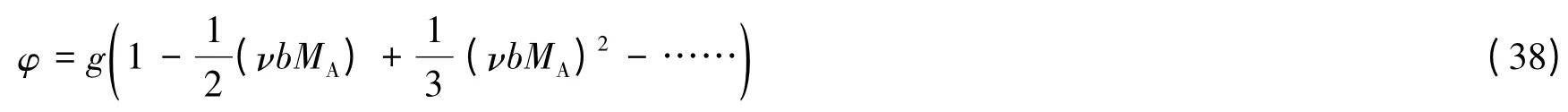
式(38)便是两种渗透因子间的换算式[4]。
[1]刘光,邱贞花.离子溶液物理化学.福州:福建科学技术出版社,1987
[2]刘国杰,黑恩成.物理化学导读.北京:科学出版社,2008
[3]傅鹰.化学热力学导论.北京:科学出版社,1963
[4]黄子卿.电解质溶液理论导论(修订版).北京:科学出版社,1983
——2017年渗透压相关高考真题赏析

