基于层次着色Petri网的创新能力演化模型及提升路径挖掘＊

王纯子，张 斌，李慧明

（1．西安工程大学 管理学院，西安710048；2．西安建筑科技大学 管理学院，西安710055）

在科技迅猛发展的今天，国与国之间的竞争已经演变为国家之间对创新人才的竞争．高等学校“十二五”科学和技术发展规划明确指出：“以创新能力提升为根本任务．……完善创新人才培养机制，努力促进高校高层次创新人才的聚集和培养能力……”．可见高校学生创新能力培养已成为我国高校首要的研究任务．如何对不同学生个体的创新能力水平进行合理、全面的评估，根据评估结果有的放矢地制定科学的创新能力培养策略，以及实施培养策略过程中的阶段性监测、控制和预测等一系列问题成为了高校创新型人才培养机制中应当给予重视的关键领域．

从19世纪60年代起至今，国内外很多学者已经开始对创新人才的能力结构、创新能力测试评价方法、培养模式和路径探索方面开展了诸多研究：在创新能力评价方面，较多采取定量评价法和定性、定量相结合的方法评价创新能力的大小．Russell F．Waugh［1］选取影响学生综合素质的要素和指标对高校学生运用Rasch模型进行综合评价．Vladan Papic［2］等人运用模糊评价方法，构建了网络专家系统．王家褀等［3］设计了高校学生创新能力综合评价指标体系，运用专家评分和精确计算互为补充的多级模糊综合评价方法和改进的AHP法，建立了高校学生创新能力多层次的分解评价模型．陆静丹［4］基于SEM 分析，在理论研究的前提下，提出了高校学生创新能力测量模型的理论构架，对假设的理论构架进行了操作化的定义并编制了问卷，最后通过对样本数据的分析，验证了高校学生创新能力测量模型的可靠性与稳定性．文献［5］构建了高等教育人才培养质量评价模型Q＝AKn＝（A0＋e1K）Kn，该模型为评价创新人才质量提供了一种新的研究思路．可以看出，现有的研究成果都是从共性的角度针对高校学生应当具备的创新能力结构而进行评价，但没有考虑高校学生个体的差异性及其就业目标需求在评价过程中起到的作用．邓岳敏博士［6］曾就中国高校人才培养与劳动力市场的对接问题进行了研究，分析了高校培养的人才在能力结构、规格等方面与劳动力市场之间的矛盾，因此高校学生创新能力培养应当跟就业问题紧密结合．

另外，国内外文献中对个体创新能力的演化趋势跟踪模拟和提升路径的研究还很少，大都集中在创新能力培养模式、培养机制、培养方法和培养内容方面的研究．各国，尤其是美国、英国、法国［7］、日本［8］等发达国家根据实际国情，一直把创新能力培养作为基本的教学传统，逐步形成了各具特色的创新人才培养模式．李嘉曾［9］提出了创新人才培养的评价机制、选拔机制和激励机制．朱宏［10］提出要积极探索研究型教学模式，将科研引入教学．目前在高校学生创新能力培养方面还没有形成一套系统化的提升方案，多数研究模式都是借鉴国外经验，分析自身不足，通过理论上的思辨来提出宏观对策，而具体到实际操作层面，产生可行性措施和具体化步骤的却不多．同时现有研究通常将高校学生创新能力的评价和培养途径割裂成两个部分，忽略了个体评价对创新能力提升的引导性作用．

文中针对现有研究中存在的不足，将目标需求引入到创新能力的评价和提升过程中，利用灰色综合评价方法建立个体创新能力和就业目标创新能力矩阵，根据矩阵中各级指标评估值分析二者的差距，以此作为制定提升策略的依据．通过构建培养行为措施集，分析个体创新能力在各个原子培养行为作用下的动态演变情况，建立基于层次着色Petri网的创新能力演化模型，该模型的层次化结构与着色技术的引入使得模型的状态空间与变迁空间得以大大降低，提升了模型的存储和运行性能．在创新能力演化模型的基础上，提出一种基于改进蚁群算法的最优提升路径搜索方法，为制定个性化的创新能力培养方案提供算法支持．

1 基于层次着色Petri网的能力演化模型设计

1．1 创新能力评价矩阵构建

某个体创新能力评估和提升问题都离不开目标需求的导向．文中为创新能力的各层指标因素评估值都创建一个与该层对应的能力矩阵，可根据实际情况在各层上选择性的制定能力需求标准．这里各层级评价指标可采用灰色综合评价法进行评估，根据实际需求对任意层级指标的灰色综合评估值设定达标阈值．为满足以上要求，做出如下定义．

定义1 个体创新能力评价矩阵集IdvMatrix．IdvMatrix＝＜fir，sec［］，thir［］［］＞为一个三元组，其中fir为对应1级评估指标的单元素矩阵，存储某个体创新能力的灰色综合评价值；sec［］＝｛sec［i］｜1≤i≤n｝为含有n个元素的行向量，存储个体创新能力的2级指标灰色评估值；thir［］［］＝｛thir［i］［j］｜1≤i≤n，1≤j≤m｝为n个行向量所组成的二维矩阵，其中thir［i］表示第i个二级指标下的三级指标向量，thir［i］［j］存储3级指标的灰色评估值，m＝thir［i］．length，对每一个thir［i］，θ取值不相同．

定义2 目标创新能力评价矩阵集TarMatrix．TarMatrix＝＜fir，sec［］，thir［］［］＞，与个体创新能力矩阵集IdvMatrix的各部分结构均相同，描述目标需求对个体创新能力的最低要求，该矩阵中各指标的达标值由实际具体需求来决定，sec［］与thir［］［］中允许部分元素值为0，即可以对某些指标无约束，但需满足下述条件：当i∈［1，5］且i∈Z，若 ∃thir［i］［j］＝＝0，则sec［i］≠0；若 ∃sec［i］＝＝0，fir≠0．

1．2 基于层次着色Petri网的创新能力演化模型定义

创新能力演化模型是用来描述在某个体的当前创新能力评价状态下，通过各种培养行为的组合性实施，一步步向目标创新能力评价矩阵逼近的状态演化模型．借助于面向对象技术对问题域的直接映射能力，将创新能力的评价、动态演变以及提升的问题转化为对对象着色Petri网模型的建立、求解的问题．不仅在问题的转化过程中不存在信息的缺失，同时能更好的利用复用和着色技术，大大降低模型中冗余库所和变迁的存储空间，提高模型的存储和运行效率，并使其可维护性增强．该模型既能保证完整描述创新能力评价信息的动态演变过程，又解决了减少大量重复变迁和相似库所数量的问题，统一了这一矛盾．

定义3 培养行为效能EFF．EFF由一个二元组＜C，P＞决定，eff＝P／C，其中C为培养行为复杂度，用于评估某项培养行为实施的难易和资源耗费程度．P为培养行为提升收益，P＝＜PC，MC＞为一个二元组，PC为主因素提升收益，衡量未达标指标的提升收益；MC为边际提升效益，衡量已达标指标的提升收益．

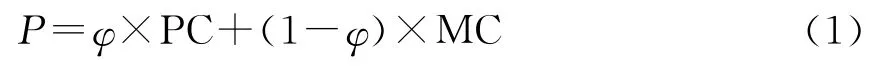
其中φ∈［0．5，1］为权重参数．

某个体的创新能力可表示为一个能力矩阵，该能力矩阵经过逐个培养行为的实施将一步步向就业目标创新能力矩阵逼近，每一种培养行为的选取都将改变当前创新能力矩阵的状态．基于以上考虑，创新能力提升演化模型需要描述创新能力系统状态、培养动作的实施、状态之间的迁移关系、以及动作与状态间的因果关系等方面的信息，因此Petri网建模方法是满足上述要求的最佳数学建模方法，具备描述创新能力状态动态演变情况的能力．

在Petri网模型中，以库所表示个体创新能力状态，以变迁表示培养行为的实施．为了反映个体在每一考察时刻的创新能力因素评估状况及能力结构的动态演变情况，可在每一时刻为所有三级指标设计一个库所，用这些库所记录该时刻下个体的指标评估值，但这样Petri网模型中的状态空间将呈36n的指数趋势急速膨胀，导致状态空间爆炸．

由于创新能力状态是由指标因素体系综合决定的，某一个体在某时刻的创新能力状态是该时刻下所有指标因素评估状态的集合，体现出一个状态包含了几种子状态的情况，因此为了解决上述问题，本文拟将对象Petri网与着色Petri网相结合进行建模，首先将创新能力综合评估状态视为一个对象，里面封装决定该综合状态的子状态，即创新能力因素库所，并给每一个库所赋予一个颜色集合．根据指标体系设计对应的对象Petri网层次化结构，顶层Petri网中的对象节点表示个体在某时刻创新能力的综合评估状态，反映了在不同时刻下其创新能力综合状态的演变情况；将顶层Petri网中的对象节点扩展，令每个对象包含n个接口库所，它反映了在不同时刻下各二级指标评估状态的演变情况．引入着色Petri网技术，给每个库所节点通过着色来表示其对应的三级指标评估状态，而非将二层Petri网继续向下扩展三层Petri网，以库所节点表示三级指标，这样可大大减少库所节点数量，降低节点空间的规模．相应的，库所间的变迁也可通过着色来表示不同三级指标状态的迁移情况，消除大量冗余变迁．

本文在对象着色Petri网的结构上进行扩展，给变迁、库所和托肯赋予相应的属性信息，来表示培养行为的实施成本和效能、各级指标评估值、因素评估值的提升力度以及路径序列等信息，从而加强模型对创新能力提升演变信息的描述能力，为最优创新能力提升路径搜索打下基础．模型示意图如图1所示．

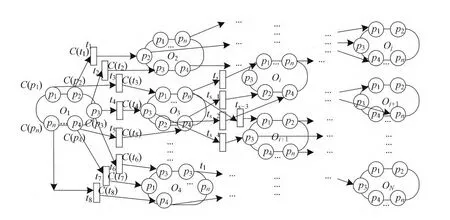
图1 层次着色Petri网模型示意图Fig．1 Hierarchical Colored Petri Net Model

由图1所示的模型可看出，以某个体的初始状态O1为起始，每当一个培养行为实施，其创新能力矩阵中所对应的一个或多个指标评价值将被提升，并生成新的个体创新能力评价矩阵（创新能力状态），若此时个体创新能力尚未达到目标创新能力评价矩阵TarMatrix中要求的各阈值，则继续实施其他培养行为并生成新的能力矩阵，直到其各项评价指标值大于等于目标合格阈值，此时模型停止搜索．不同的培养行为实施组合将生成不同提升路径，并最终形成多个达标终端对象（如图中Oj，Oj＋1，…ON）．

图1中每个库所和变迁上都对应一个颜色集合C．当两两对象节点之间有多个变迁时，这些变迁表示的培养行为意义相同，说明一种培养行为可以提升多个二级指标．当某个培养行为实施时，将相继引发相对应的一个或者几个三级指标和二级指标评估值发生改变，触发创新能力状态对象及其中的库所发生迁移，并产生新的创新能力状态对象．Petri网中的对象和库所均可以复用，在代码实现时将对象和库所设计为聚合关系，复用的对象和库所只需分配一块存储空间，并被多个引用它的对象指针指向即可．这样的对象Petri网结构不仅能够直接反映指标评估这一问题域，清晰表达不同指标层级下个体创新能力的动态演变情况．同时还能够减少每层Petri网上节点的相对数量，并依靠复用和着色技术减少存储空间的绝对数量，提高模型性能．

通过上述分析，采用层次着色Petri网来建立创新能力演化模型，定义为．

定义4 基于层次着色Petri网的创新能力演化模型 ACAEM＿EOCPN＝（O，PJ，T，TS，C，P-，P＋，IdvMatrix，λ，σ，μ，Tok，I（ti），O（ti），O（Oi））其中：

O＝｛O1，O2，…，ON｝是创新能力状态对象集，Oi＝（O，PJ，T，C，IdvMatrix，σ，Tok），0＜i≤N，对象节点不包含内部库所和变迁．

PJ＝｛O1．p1，O1．p2，…，O1．p5，…，Oi．p1，Oi．p2，…，Oi．p5，…，ON．p1，ON．p2，…，ON．p5｝，PJ为接口库所的有限集合，Oi．pj∈PJ，表示对象Oi中的库所pj．Petri网中每一个对象Oi包含5个子状态（库所），分别对应指标体系中的5个二级指标，记为｛Oi．pj｜1≤j≤5｝，且pj∈｛pcm，pkw，pth，pab，pinn｝．

T＝｛t1，t2，…，tm｝是培养行为变迁的有限集合，ti∈T，m表示顶层Petri网中变迁的个数，且m＞0；P∩T＝∅．

④ TS＝｛TSij｜0＜i≤N，0＜j≤N｝是对象间的变迁集集合，其中TSij表示从状态对象节点Oi到节点Oj的变迁集．

C（pj）＝｛pj1，pj2，…，pjn｝，其中n表示二级指标状态pj中所包含的三级指标状态个数．C（ti）＝｛ti1，ti2，…，tir｝，其中tir表示培养行为ti的发生而触发的输入库所中第r个三级指标状态发生的转移．

P-与P＋分别为变迁的输入弧和输出弧的迁移函数：P-，P＋：C（ti）→C（pj），表示变迁色为tix∈C（ti）的变迁ti的输入（输出）库所色为pjy∈C（pj）的库所pj．激发规则：∀ti∈T，若P-（tix）＝pjy，则P＋（tix）＝pjy．

IdvMatrix＝｛IdvMatri xi｜0＜i≤N｝，IdvMatrix的定义见定义1，IdvMatri xi与顶层Petri网中的对象 Oi一一对应，IdvMatri xi．fir记录个体创新能力灰色综合评估值，IdvMatri xi．sec［j］与对象Oi中的库所pj一一对应，IdvMatri xi．thir［j］［k］与对象Oi中的库所pj的颜色因素pjk一一对应．

λ＝｛λij｜0＜i≤N，0＜j≤N｝，λij与变迁集集合TS中的元素一一对应，表示各培养行为实施的复杂度；

σ＝｛σj｜σj＝｛σj1，σj2，…，σjn｝｝，其中σj与PJ中的元素一一对应，σjy与C（pj）中的元素一一对应，记录各三级指标的原始评价量化值．

μ＝｛μi｜μi＝｛μi1，μi2，…，μin｝｝，其中μi与T中的元素一一对应，μix与C（ti）中的元素一一对应，记录培养行为ti对各三级指标评估值的提升力度．

Tok＝TokO∪TokP，TokO为对象托肯集，用来记录路径信息；TokP为库所托肯集，用来激发变迁．TokO＝（rout＝O1TS12O2TS23，…，TSinOn；REFF）中每个托肯都存储一个数据结构，用来携带提升路径上的信息，其中rout记录路径序列；REFF为个体创新能力提升路径的效能函数，它表示了托肯从个体创新能力的初始状态对象到达终端对象所经过的提升路径的综合培养效能值，其计算公式见定义7．

I（ti）表示变迁ti的输入库所，I（ti）∈PJ；O（ti）表示变迁ti的输出库所，O （ti）∈PJ；

O（Oi）表示对象Oi的输出变迁集集合，O（Oi）＝｛TSij｜Oj为Oi的下一时刻的迁移对象｝．

定义5 设某个体在时刻t所处的创新能力状态为Oi，从状态对象节点Oi到节点Oj的变迁集为TSij，此刻未达标指标集合为Unq，达标指标集合为Qua，则TSij所表示的培养行为的主因素提升收益和边际提升收益为

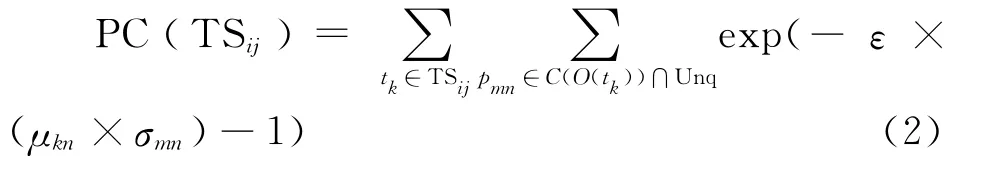
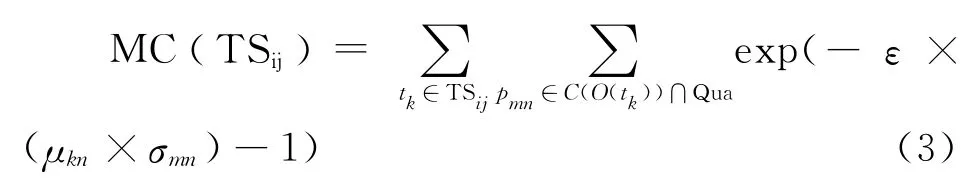
其中，ε∈（0，10］为调节参数．

定义6 提升路径培养效能REFF．REFF是衡量从某个体创新能力初始状态演变到当前状态所经历培养行为路径的综合提升效能的评价指标，其计算公式为

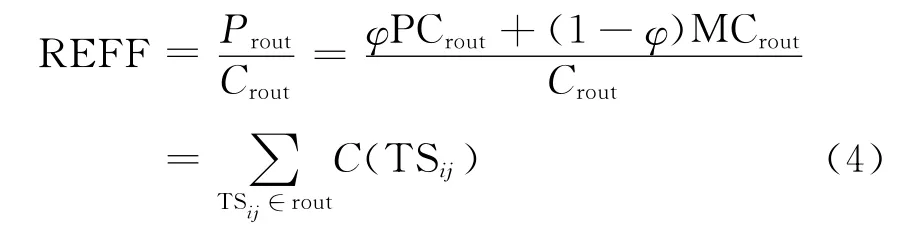
其中，pjy∈Unq＆＆Ox．py≠O1．py＆＆Ox∈rout表示路径rout能够提升的所有未达标三级指标pjy集合；pjy∈Qua＆＆Ox．py≠O1．py＆＆ Ox∈rout表示路径rout能够提升的所有已达标三级指标pjy集合；ti∈rout ＆＆ O（tiy）＝ pjy表示路径rout中对指标pjy有提升作用的变迁ti集合．

2 基于ACAEM＿EOCPN模型的创新能力提升路径生成方法研究

在基于层次着色Petri网的创新能力演化模型上，采用蚁群算法进行寻路，以初始对象节点为起始，该节点记录了某个体当前创新能力评价矩阵的初始状态值，通过培养行为变迁的一步步触发，该个体创新能力评价矩阵按照目标评价矩阵中要求的阈值向模型中的各个达标矩阵一步步逼近．

2．1 基于蚁群算法的提升路径搜索机制设计

以托肯模拟蚂蚁在ACAEM＿EOCPN模型的顶层Petri网上寻路，即对象托肯集TokO中的托肯在运行的每一步按照一定的概率选择要执行的培养行为，则该行为在当前阶段所对应的变迁集触发，使一个或多个库所状态发生迁移，并令当前对象节点跃迁到新的对象节点．

定义7 同种路径．设两条路径rout1＝O1TS12O2TS23，…，TSimOm，rout2＝O1TS14O4TS45，…，TSjnOn，定义培养措施集 TS（routx）＝｛TSij｜TSij∈routx｝，如果 TS（rout1）＝ TS（rout2），则rout1与rout2为同种路径，记为rout1∽rout2，∽关系具有自反性、对称性和传递性．

定义8 说明同种路径的培养措施集完全相同，只有培养行为执行先后顺序不同，因此创新能力提升路径的效能也相同．在托肯寻路过程中，一组同种路径中只需保存其中任意一条即可．

eff＝ ｛eff1［k］，eff2［k］，…，effn［k］｝，与ACAEM＿EOCPN中每一个终端对象Oi一一对应，effi［k］（i＝1，2，…，n）是一个数据结构数组，其中每一个元素与TokO中元素的数据结构相同，effi［k］存储着达到终端对象Oi（i＝1，2，…，n）的所有托肯中，提升路径的效能函数值最大的k个托肯元素；τ＝｛τ1，τ2，…，τm｝与 TS＝｛TSij｜1≤i，j≤n｝中的元素一一对应，存储对应变迁集上的信息素，是托肯选择培养行为的主要依据．

由于可能存在几条提升路径到达同一终端对象的情况，定义9令每个终端对象存储到达该对象的k条效能最优的提升路径．

定义9 变迁集信息素的局部更新规则．对于终端对象中的托肯，它所记录的路径效能REFF越大，路径上的变迁集信息素浓度也应该越大．对于该托肯所记录的路径序列中的变迁集TSij，信息素奖励规则为

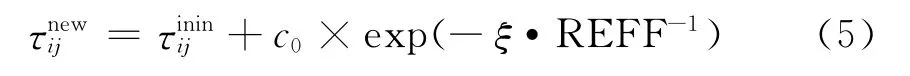
式中，c0是一个常数，表示路径效能对信息素的奖励基础值，ζ为调整参数．

由于同种路径的培养策略集相同，对个体创新能力的提升结果相同，提升效能也相同，因此只需保存一条路径即可，并对其它同种路径给予信息素惩罚．同种路径中各变迁集上信息素的惩罚力度不同，某变迁集信息素比重越高，说明通过该变迁集的非同种路径越多，且效能越高，则惩罚力度应当越小，反之，变迁集信息素比重越低，则通过该变迁集的路径越少，效能越低，则惩罚力度应当越大．对同种路径上的变迁集信息素按照其所占比重来决定惩罚力度，能够有效使得蚁群算法尽快收敛于一条最优路径上，同时也避免了搜索退化现象．基于以上考虑，提出以下信息素惩罚规则．

设某一终端对象为Oi，对于某一运行到Oi的托肯tokj，若 ∃effi［x］∈Oi，effi［x］．rout∽tokj．rout且effi［x］．rout≠tokj．rout，则对tokj．rout所记录的变迁集进行信息素惩罚，惩罚规则如下：∀TSij∈tokj．rout，

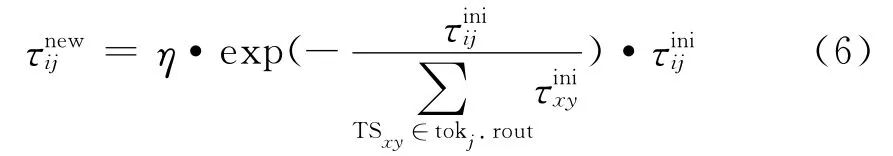
其中η∈（0，1）为调节参数．

定义10 变迁集信息素的全局更新规则．蚁路上信息素是时刻在挥发的，所以还需要对所有变迁的信息素进行全局更新．在Petri网系统中，每隔单位时间，用公式（11）（12）对所有变迁集TSij的信息素进行全局更新：

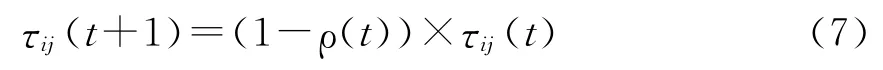
式中，τij（t）和τij（t＋1）分别是t时刻与下一时刻时TSij上信息素的浓度．其中ρ为一个自适应调整的可变量，每隔单位时间，ρ值逐渐减小，另一方面，信息素浓度越大，挥发的越快，具体取值为

其中，γ为挥发约束系数，0＜γ＜1．这种ρ值的设计能够保证算法既能广泛搜索又能快速收敛．

定义11 托肯的选路规则．当对象托肯有多个变迁集可选择时，根据可选变迁集的信息素浓度及其提升效能来概率性的选择路径．选路规则为

式中，α，β为控制信息素和效能值之间的相对重要性参数．

定义12 全局干扰托肯．为了解决搜索算法陷入局部极优的问题，在算法每轮迭代开始时，选择一部分对象托肯为全局干扰托肯．这类托肯将优先选择信息素少的变迁，其数量随着迭代次数的增加而减少．这样在迭代初期，使托肯集尽可能遍历到每一条路径，发现更多新解，从而避免可行解快速陷入局部最优；同时在迭代后期，算法搜索结果趋于稳定，减少干扰托肯以增强全局最优的收敛能力．随机托肯数量确定方法为

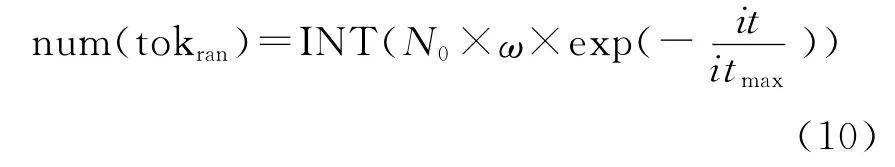
式中：N0为每轮迭代放置于初始对象中的托肯总数；it为算法当前迭代次数，itmax为算法最大迭代次数；ω∈（0，1）为调节参数．

干扰托肯的选路规则为

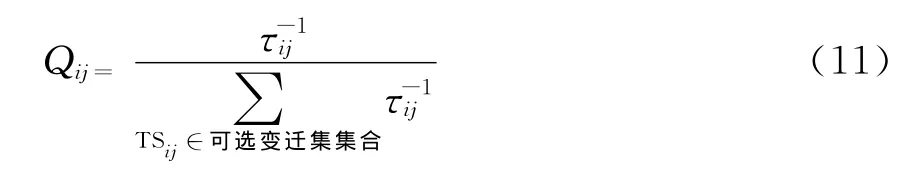
公式（14）说明干扰托肯的作用在于广泛遍历路径空间中未搜索或搜索次数少的路径，其选路规则与变迁集效能无关．

2．2 最优提升路径搜索算法设计

根据ACAEM＿EOCPN模型以及蚁群算法过程描述，设计算法步骤为

Algorithm：OptAdvRoutSearching（＊head）；

Input：某一个体创新能力演化模型ACAEM＿EOCPN；

Output：optRout［k］；

Description：

初始化各参数，输入基础数据 N0，φ，ω，τ0，k，c0，ζ，η，γ，ρmin，α，β；

在初始对象节点O1中放置N0个对象托肯，在ACAEM＿EOCPN模型上遍历最优提升路径；

根据公式（13）计算随机干扰托肯数量num（tokran），并创建随机托肯集 RTok；

for（r＝0；r＜N0；r＋＋）；

｛m＝0；n＝0；

for（i＝1；Oi∉finalObj［］；i＝j）／／finalObj［］为终端对象集；

｛Qmax＝0；

while（∀TSij∈O（Oi））；

｛if（tokr∉RTok）；

｛根据公式（4）（5）（6）计算 P（TSij）；EFF（TSij）＝P（TSij）／λij；

根据公式（13）计算 Qij；

if（Qij＞Qmax） ｛m＝i；n＝j；｝｝

if（tokr∈RTok）；

｛根据公式（14）计算Qij；

if（Qij＞Qmax） ｛m＝i；n＝j；｝｝；

while（∀tx∈TSmn）／／选择变迁集TSmn为待实施培养行为

｛while（∀py∈I（ti））；

生成库所托肯py．tokl∈TokP；｝／／库所托肯负责激发变迁；

生成新对象托肯On．tokr∈TokO；

On．tokr．rout＝Om．tokr．rout＋”TSmnOn”；

删除对象托肯Om．tokr；

｝；

for（i＝0；i＜On．effn［k］．length；i＋＋）；

if（On．tokr．rout∽On．effn［i］．rout）｛根据公式（9）对On．tokr．rout中记录的变迁集进行信息素惩罚更新；break；｝；

else｛根据公式（7）计算On．tokr．rout．REFF；

if（On．tokr．rout．REFF＞On．effn［i］．rout．REFF）将On．tokr插入到On．effn［i］位置处；根据公式（8）对On．tokr．rout中记录的变迁集进行信息素奖励更新；｝；

每隔单位时间，按照式（10）～（11）对变迁信息素进行全局更新；

判断蚁群算法是否已循环规定的次数，如果满足条件则算法终止，取所有终止托肯中所记录路径效能最大的k条路径存入optRout［k］，即optRout［k］＝max＿k｛Oi．effi［x］｜Oi∈finalObj［］｝，算法结束；否则，跳转至Step 2．

3 实例分析与验证

以高校学生为例，说明ACAEM＿EOCPN模型的建立和最优提升路径的搜索方法．通过对已有参考文献［3-5］进行总结和分析，将各指标要素划分知识、思维、能力、个性以及创新技能五个维度，建立如图2所示的高校学生创新能力的评价指标体系．

某陕西高校信息管理专业大三学生的择业目标为IT企业中的研发岗位．按照图2所示指标体系对其个体创新能力进行量化综合评估，得到初始个体创新能力矩阵集IdvMatrix1≤fir，sec［5］，thir［5］［］＞，通过对多家国内外独资、合资IT企业的研发部门和人事部门展开调研并进行综合评估，得到其TarMatrix矩阵．通过对比IdvMatrix1与TarMatrix，建立未达标指标集 Unq＝｛v13，v15，v24，v25，v310，v311，v46，v47，v48，v49，v51，v52｝．可选的创新能力培养行为有7种，见表1．

根据ACAEM＿EOCPNGenerate算法，可生成如图3～4所示的ACAEM＿EOCPN模型．每个对象包含5个接口库所，分别为：知识要素评估库所（kw）、思维要素评估库所（th）、个性动机评估库所（cm）、能力要素评估库所（ab）以及创新要素评估库所（inn），生成二层Petri网．

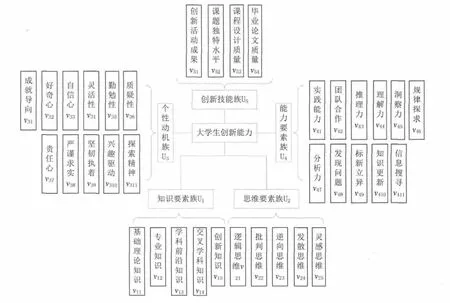
图2 创新能力评价指标体系Fig．2 Innovative capability evoluation index hierarchy system

表1 可选培养行为Table 1 Optional cultivation activities

图3所示的顶层Petri网描述了该生的创新能力状态对象从初始状态开始在各种培养行为作用下的演化状体全集，其中灰色表示终端对象，对象Oi与对象Oj之间通过变迁集TSij引发状态迁移，TSij上的数字表示该变迁集所对应的培养行为序号．顶层Petri网中的每一个变迁集和对象节点均可扩展下层网，例如将图中虚线方框内的Petri网扩展，可得如图4所示的二层Petri网．

调用最优提升路径搜索算法OptAdvRout-Searching（＊head）在ACAEM＿EOCPN模型上搜索效能最大的k条提升路径，算法中涉及的各参数取值如下：初始对象O1中放置托肯数为N0＝20，算法最大搜索次数为150，φ＝0．7，τ0＝10，ω＝0．4，k＝3，c0＝10，ζ＝0．8，η＝0．85，γ＝0．3，ρmin＝0．1，α＝0．6，β＝0．4，ε＝3．当算法迭代约100次时，在ACAEM＿EOCPN模型上最优路径已基本凸显，当完成150次迭代后，算法输出的3条最优路径为：optRout［0］＝（rout＝O1TS13O3TS3＿13O13TS13＿39O30；REFF＝3．698339），optRout［1］＝（rout＝O1TS13O3TS3＿11O11TS11＿28O28；REFF＝3．143988），optRout［2］＝（rout＝O1TS16O6TS6＿17O17TS17＿36O36TS36＿58O58；REFF＝2．982456）．由生成的创新能力演化模型以及算法的输出结果可以看出，一共有25条提升路径可供选择以达到该学生就业目标需求，其中最优的三条路径所对应的培养行为序列分别为：2→5→6，2→3→6，5→6→7→2．实验结果说明，假期参加社会实践活动虽然复杂度（实施成本）比增强课程设计环节要高，但其要求学生在实习企业的基层岗位投入工作并开展相关调研，撰写调研报告和论文，该培养行为对学生的各项综合能力指标有更大的提升，因此2→5→6为最优效能路径．5→6→7→2路径的总收益值虽然比前二者高出很多，但参于指导教师的科研项目需要相对严格的前提条件，该学生必须先通过 （3，5）或6号行为的实施提升部分不满足条件的指标，然后再接受7号培养行为，因此该路径的复杂相对也高出很多，从总体培养性价比的角度考虑，其效能要低于前两种．

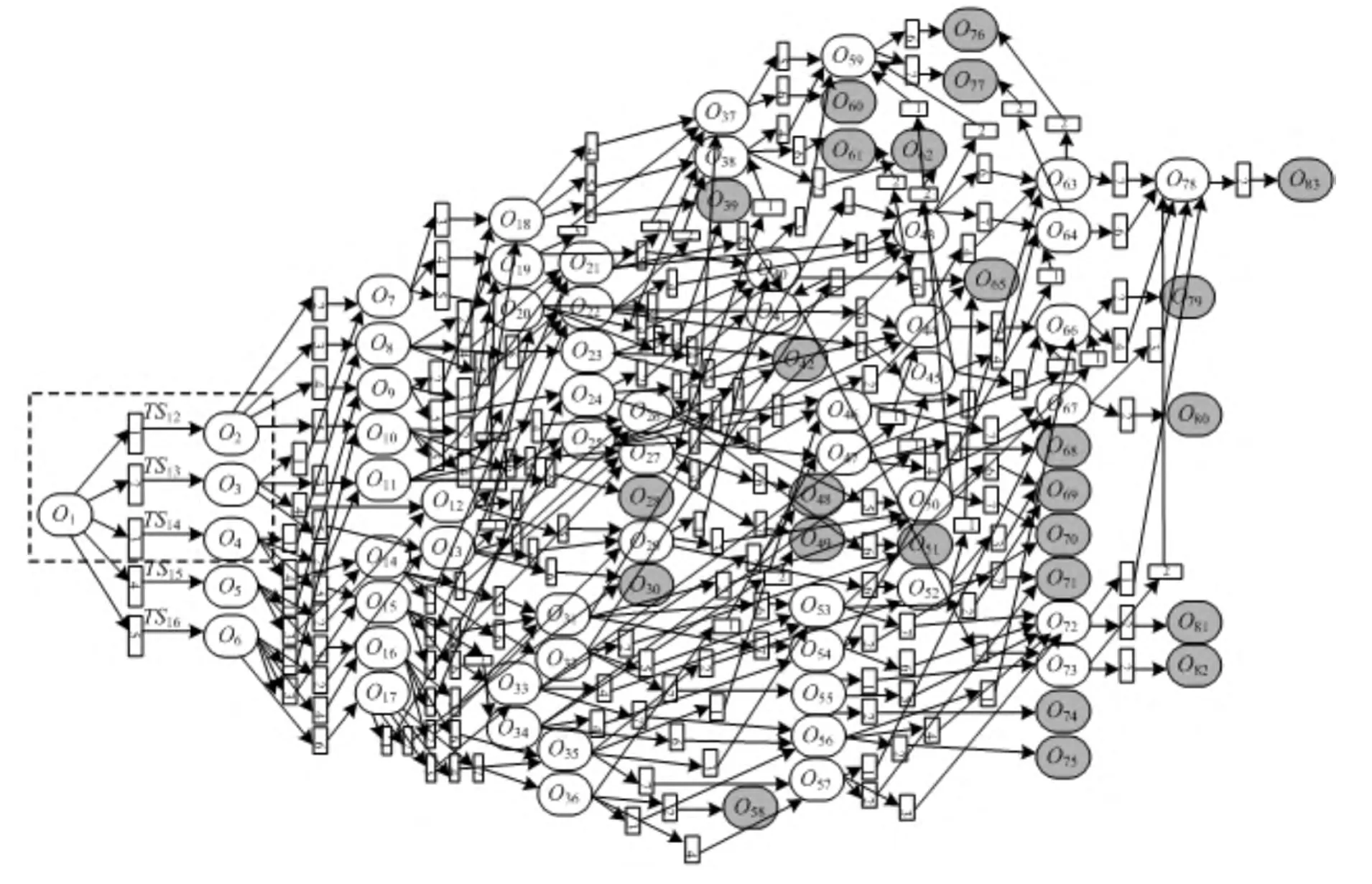
图3 某学生创新能力演化模型顶层Petri网Fig．3 Top level petri net of a college student’s innovative capability evaluation model

图4 局部二层Petri网示意图Fig．4 Partial second level petri net

实例分析表明，该本科生要满足IT企业中的研发岗位的能力需求，必须在现有的能力结构基础上，通过选修延伸性、交叉性知识课程，假期参加社会实践活动，参加学生创新创业比赛来提升自身能力结构中的薄弱因素，该培养路径相比较其他路径而言成本最低，效能最优，

4 结 论

从一个新的视角提出了以目标为导向的创新型人才培养模式，能够科学地对个体创新能力的评估、创新能力演化情况的实时监控以及创新能力的个性化提升方案的制定，有目的性的为社会各岗位培养专业化的创新型人才，推动社会先进技术和生产力的发展．以高校学生为例，针对高校教育与市场需求对学生创新能力的供需问题，尝试建立高校学生创新能力评价指标体系，开展了高校学生创新能力提升路径研究．

［1］ RUSSELL F．WAUGH．Quality of Student Experiences at University：A Rasch Measurement Model analysis［J］．Australian Journal of Education，2001，45（2）：183．

［2］ VLADAN P，NENAD R．Vladimir Pletina．Ldentification of Sport Talents Using a Web-Oriented Expert System with a Fuzzy Module［J］．Expert Systems With Applications，2009，36（5）：8830．

［3］ 王家褀，曹颖颐．大学生创新能力综合评价研究［J］．武汉理工大学学报：信息与管理工程版，2007，29（8）：133．WANG Jia-qi，CAO Ying-yi．Comprehensive Evaluation Innovative Capability of College Students［J］．Journal of WUT：Information and Management Engneering，2007，29（8）：133．（in Chinese）

［4］ 陆静丹，陈培玲．基于SEM的大学生创新能力测量模型［J］．统计与决策，2011（3）：71．LU Jing-dan，CHEN Pei-ling．College Students’Innovative Capability Measuring Model Based on SEM［J］．Statistics and Decision，2011（3）：71．（in Chinese）

［5］ 马万民．高等教育人才培养质量评价模型研究［J］．中国软科学，2008（8）：153．MA Wan-min．Research on Evaluation Model of Higher Education Talents Cultivation Quality［J］．China Soft Science，2008（8）：153．（in Chinese）

［6］ 邓岳敏．改革开放以来中国高校人才培养与劳动力市场的对接问题研究［D］．厦门：厦门大学，2007．DENG Yue-min．A Study on the Connection of Talents Training of Higher Education Institution and Labor Market in China Since the Adoption of Reform and Opening-up Policy［D］．Xiamen：Xiamen University．2007．（in Chinese）

［7］ 李兴业．法国高等工程教育培养模式及其启示［J］．高等教育研究，1998（2）：98．LI Xing-ye．France Higher Engineering Education Training Mode and Enlightenment［J］．Journal of Higher Education，1998（2）：98．（in Chinese）

［8］ 胡建华．大学审议会与日本高等教育改革［J］．中国高等教育，2001（12）：41．HU Jian-hua．The University Council and the Higher Education Reform in Japan［J］．China Higher Education，2001（12）：41．（in Chinese）

［9］ 李嘉曾．高等教育大众化与建立创新人才培养机制［J］．科学学与科学技术管理，2001（7）：62．LI Jia-zeng．The Popularization of Higher Education and the Establishment of Innovative Talent Training Mechanism［J］．Science of Science and Management of S．＆ T，2001（7）：62．（in Chinese）

［10］ 朱宏．高校创新人才培养模式的探索与实践［J］．高校教育管理，2008，2（3）：6．ZHU Hong．An Exploration of Innovative Talent Producing Mode in Colleges and Universities［J］．Journal of Higher Education Management，2008，2（3）：6．（in Chinese）