振动信号离散余弦变换域循环维纳滤波算法＊

张 峰，胡艳涛，石现峰

（西安工业大学 电子信息工程学院，西安710021）

基于振动信号分析的机械故障诊断方法具有可在线、实时、非损伤、诊断便捷准确等优点，对于保障机械设备的安全、稳定运行具有重要意义［1］．振动信号在获取和传输过程中，不可避免会受到环境和设备自身噪声的干扰，不能真实地反映旋转机械的运行状态，影响后期的分析和处理，甚至于可能会造成误判［2］．因此，要获得振动信号的准确特征并依据这些特征进行汽轮机运行状态的检测和故障诊断，必须首先进行振动信号的去噪处理．

传统滤波技术，在滤波效果和线性相位之间不易取得较好平衡，而振动信号滤波对相位要求严格，不允许产生明显的相位失真．文献［3］利用循环维纳滤波实现振动信号的自适应噪声滤除，取得了较好的效果，但是直接循环维纳滤波对非平稳随机信号滤波效果差，而自适应滤波算法复杂运算量大；文献［4］基于离散余弦变换（Dicrete Cosine Transform，DCT）进行振动信号无相移滤波的方法，保证了信号的相位特性，实现了数据量的压缩，但DCT滤波存在对长数据滤波效果差的问题；文献［5］将软阀值法小波滤波应用于振动信号滤波，取得了很好的滤波效果，但是该算法需估计噪声方差，也存在阀值选取困难的问题．

文中在对振动信号特点及滤波要求进行分析的基础上，提出了振动信号离散余弦域循环维纳滤波算法，在保证相位特性取得较好滤波效果的同时，也可实现对数据的压缩．

1 振动信号采集及滤波要求

1．1 振动信号采集

对工业现场的汽轮机振动信号进行了采集．数据采集的相关参数采用32倍频采样，即转速的32倍，配合后面的快速傅里叶变换（Fast Fourier Transformation，FFT）计算的需要，采样点数设成2的整数次幂，即N＝2M．同时为了方便处理，每通道连续采集128点［6］．所采集的信号波形如图1所示，为研究去噪性能，故对信号加入随机噪声，加噪后的振动信号如图2所示．

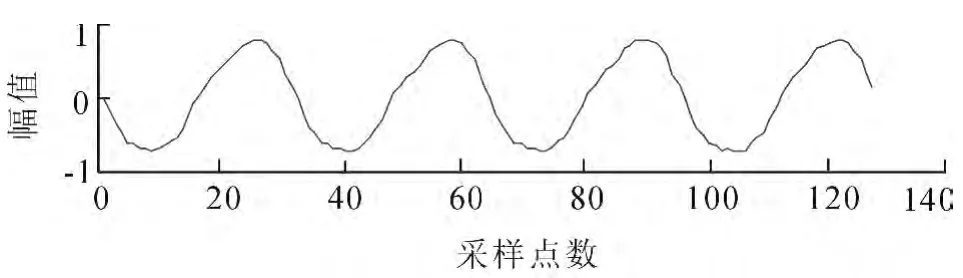
图1 原始采集振动信号Fig．1 Original sampling of vibration signal

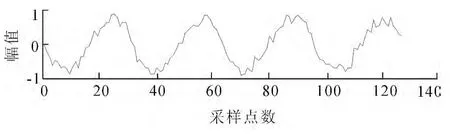
图2 加噪处理后的振动信号Fig．2 Vibration signal after being added noise

1．2 振动信号滤波要求

为了尽可能准确地获取汽轮机运行状态，对汽轮机振动信号的去噪处理一般需满足如下两点基本的要求：

① 振动信号各次谐波相位信息包含了转轴振动的位置信息，因此必须要保证信号滤波后不产生或者较少产生相位失真．滤波算法相频特性的非线性会引起波形的畸变，这种畸变正是相位失真的一种表现．所以，这就要求滤波算法具有较好的线性相位特性．

②在保证相位特征的前提下，能够有效滤除噪声，获取最真实的反映汽轮机运行状况的振动信号．尤其在后续振动信号的谱估计中，噪声对谱估计算法的方差性能以及谱估计的准确程度会有非常大的影响，需要尽可能的去除噪声的干扰．

2 DCT域的信号滤波与压缩处理

2．1 离散余弦变换

离散余弦变换是一种实数域的正交变换，对长度为N的序列x（n），其离散余弦变换用Xc（k）表示，定义为

离散余弦变换具有高度解相关性，变换以后的数据相关性降低，信号大部分能量只集中在少数几个变换系数上，并且这些变换系数表征的都是信号的低频能量［7］．所以抛弃后面的数据依然可以保留信号特征，同时除去了后面系数混叠的噪声，并且减少数据量起到压缩数据的作用．利用DCT信号去噪的一般过程为：先将输入数据按式（1）进行DCT变换；将变换后的数据根据能量集中的效率保留前面的数据，抛弃后面的数据；然后把保留的数据补0到原始数据长度；再按式（3）进行DCT逆变换，获得滤波后的数据［8］．

2．2 DCT滤波效果分析

基于DCT的信号去噪是一种无相移的滤波方法，但其滤波效果取决于所保留的DCT变换系数的个数［4］．利用上述算法对图2所示加噪后的振动信号滤波效果并同原始信号进行对比后的结果，如图3所示．

图3 利用DCT去噪后的汽轮机振动信号Fig．3 TurbineVibration signal after being filtered by DCT

由图3（a）可看出，当保留的系数较少时，能够在较大程度上滤除噪声的干扰，但滤波后信号的波形过于平滑，产生了明显失真．产生这一问题的原因是，使用DCT进行滤波时抛弃了后面的部分，若保留点数过少，则丢失能量过多，复原后不能很好表征原始信号．

由图3（b）可看出，当保留的系数较多时，滤波效果明显变差，很多噪声干扰无法得到有效去除．这是由于DCT滤波是直接抛弃了DCT变换后后边的系数及其叠加的噪声，而前面的系数所叠加的噪声则完全保留了下来．

离散余弦变换应用于汽轮机振动信号的滤波虽然能够起到一定的去噪作用，但其为非线性滤波，需要选取合适的保留长度，舍弃过少噪声无法有效滤除，舍弃过多则信号本身信息也会损失过多．另外，当信号采集长度较长时，信号DCT域能量集中程度降低，这种取舍会更加困难．所以，该算法直接用于振动信号滤波还存在一定问题，对于较长数据可以先周期分段再进行处理．

3 循环维纳滤波算法

维纳滤波是基于最小均方误差的线性滤波器，可以设计成有限冲激响应（Finite Duration impulse Response，FIR）的也可以设计成无限冲激响应（Infinite Duration Impulse Response，IIR）的．以FIR维纳滤波为例，其基本原理如图4所示．

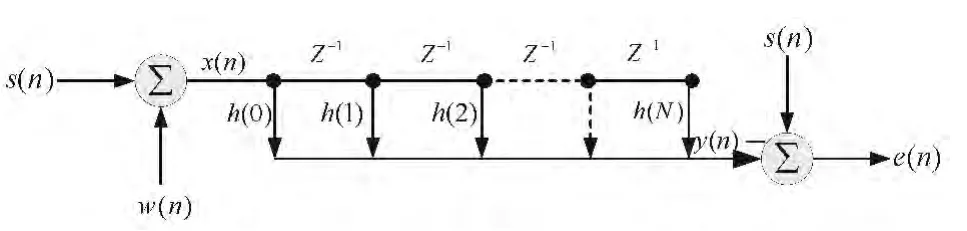
图4 wiener滤波算法原理图Fig．4 Winner filter schematic

图4中，s（n）为真实信号；w（n）为加性噪声或测量误差；x（n）为观测信号；h（n）为维纳滤波器系数；y（n）为维纳滤波输出信号；e（n）为处理误差．由图4可知：

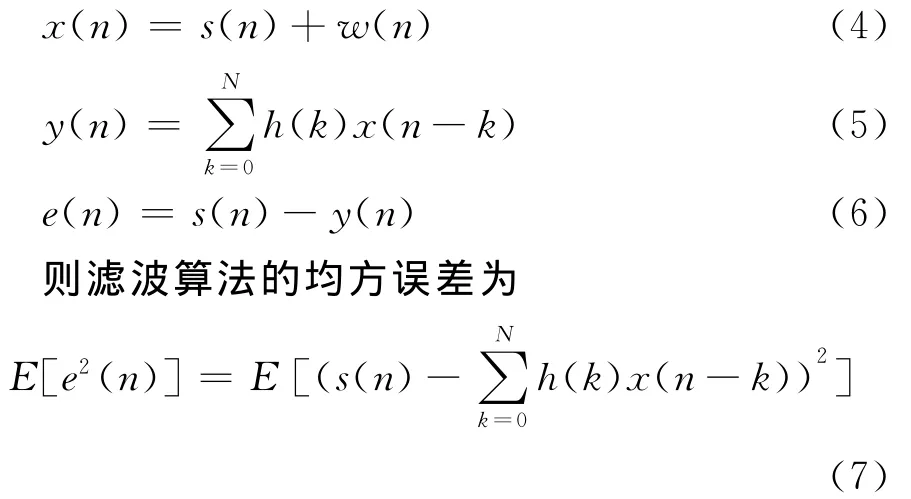
最小均方误差的准则，即上式的值最小．因此维纳滤波器的加权系数h（k）应满足以下的线性方程组

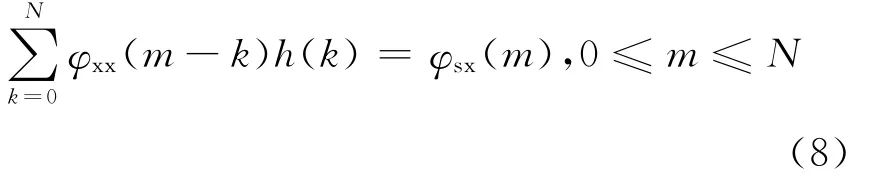
式中：φxx（m）为观测信号的自相关序列；N为维纳滤波器的阶次；φsx（m）为理想信号与观测信号的互相关序列［9］．

维纳滤波器要求信号是平稳的，严格来讲采集于工业现场的振动信号是非平稳信号，不能直接使用维纳滤波．但振动信号具有一定的周期平稳性．当信号具有较明显的周期性时，可用循环维纳滤波器对数据进行分段循环处理，即将一整段的原始振动信号按照一定规则进行小范围分割，在每个小的范围内分别采用维纳滤波，并以此形成循环，在后期再把数据分段进行线性整合．循环维纳滤波器是维纳滤波器的改进，其滤波效果优于直接进行维纳滤波，并且在较低阶次时依然有较好的滤波效果［10］．循环维纳滤波仿真结果如图5所示．

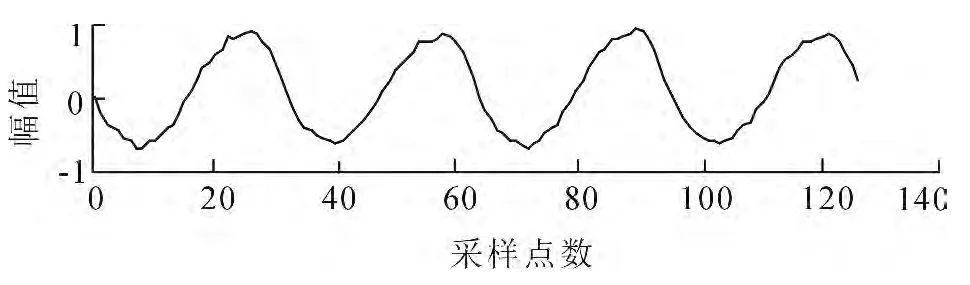
图5 循环维纳滤波仿真结果Fig．5 Simulation result of cyclic Wiener filter

4 DCT域循环维纳滤波

4．1 DCT与循环维纳滤波的结合

直接DCT滤波时，系数保留部分叠加的噪声无法滤除，可使用维纳滤波器对其再次滤波以提高滤波效果．当信号长度较长时，DCT变换的能量集中程度降低，并且对维纳滤波阶次的要求也随之提高，所以可以考虑分段后在DCT域再对其进行维纳滤波．振动信号一般来讲具有循环平稳的特点，可以将振动信号先进行整周期分段，对每段分别进行DCT变换后再逐段进行维纳滤波，即DCT域循环维纳滤波．两者的有机结合即弥补了DCT滤波的不足，也更好的发挥了维纳滤波的作用．DCT域进行循环维纳滤波的算法过程如下：

① 对观测信号和理想信号按相同规则分别进行分段；

② 对每一段分别进行离散余弦变换；

③对第一段DCT变换后数据进行维纳滤波处理，得到的结果保存留用；

④ 将上一段滤波结果作为下一段滤波处理的期望信号；

⑤ 将处理完毕的若干段信号依据原始次序进行简单的组合；

⑥ 对重组数据进行反余弦变换，得到滤波结果．

4．2 滤波结果分析

从算法原理分析，DCT滤波是零相移或无相移滤波，选择最优的保留长度，可以取得一定的滤波效果并且不明显丢失波形信号特征，而循环维纳滤波是一种线性滤波，所以整体看来可以取得较好的相位特性；DCT滤波去除了后面系数叠加的噪声，再进行循环维纳滤波可以进一步提升滤波效果；利用DCT域能量集中原理加之分段处理，可以大大降低维纳霍夫方程阶次．这样一来便可以很好的解决前面所提及的问题．

DCT域循环维纳滤波算法仿真结果如图6所示，从实际仿真结果可以看出这不仅取得了较好的噪声滤除效果，最大程度的进行了噪声与信号的分离，并且很好的保留了原始信号的特征，同时也获得了很好的相位特性．

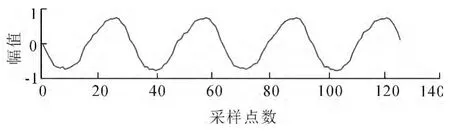
图6 DCT域循环维纳滤波仿真结果Fig．6 Simulation result of cyclic winner filtering in DCT domain

实践表明，本文所提出的振动信号离散余弦变换域循环维纳滤波算法能够满足该类振动信号的滤波需求，同时也实现了对数据的有效压缩，减少了数据量．

5 结 论

文中提出了振动信号离散余弦变换域维纳滤波算法．该方法将DCT滤波和循环维纳滤波有机结合，从而达到更好的滤波效果．仿真结果表明该算法在对汽轮机振动信号的去噪处理中取得了较为理想的效果，能够保证较好的相位特性，用于振动信号的滤波处理不产生明显的相位失真；并且在保证相位特性的同时，取得了较好的滤波效果，性能优于单独使用DCT滤波算法和维纳滤波算法．算法中对数据进行了分段处理，降低了维纳滤波运算阶次，解决了DCT对长数据能量集中程度降低的问题，利用DCT的能量集中特点，又进一步降低了运算的阶次，同时还可以实现对振动信号数据量的压缩．此算法的基本原理也可应用于其它具有相似滤波要求的信号去噪处理中，有很好的实用价值和应用前景．

［1］ 张君，王金平，朱波．旋转机械振动信号处理中的滤波及特征提取技术［J］．南京工程学院学报：自然科学版，2009，7（03）：15．ZHANG Jun，WANG Jin-ping，ZHU Bo．Signal Filtering and Feature Extraction Technology of Rotating Machinery Vibration Signal Process ［J］．Journal of Nanjing Institute of Technology：Natural Science Edition，2009，7（03）：15．（in Chinese）

［2］ 王景芳．DCT域维纳滤波语音增强［J］．湖南涉外经济学院学报，2014，14（01）：83．WANG Jing-fang．On DCT Domain Wiener Filtering for Speech Enhancement［J］．Journal of Hunan International Economics University，2014，14（01）：83．（in Chinese）

［3］ 明阳，陈进，董广明．基于循环维纳滤波器和包络谱的轴承故障诊断［J］．振动工程学报，2010，23（5）：537．MING Yang，CHEN Jin，DONG Guang-ming．Rolling Bearing Fault Diagnosis Based on Cyclic Wiener Filter and Envelop Spectrum［J］．Journal of Vibration Engineering，2010，23（5）：537．（in Chinese）

［4］ 管博，胡劲松．基于DCT的旋转机械振动信号无相移滤波方法研究［J］．汽轮机技术，2007，49（04）：285．GUAN Bo，HU Jin-song．Study of the DCT-Based Vibration Signal Zero Phase Distortion Filtering Method in Rotating Machinery［J］．Turbine Technology，2007，49（04）：285．（in Chinese）

［5］ SINGH G K，SALEH A l K S A．Vibration Signal A-nalysis Using Wavelet Transform for Isolation and I-dentification of Electrical Faults in Induction Machine［J］．Electric Power Systems Research，2003，68（2）：119．

［6］ 王金平，邓艾东，丁轲轲．基于DSP的汽轮机振动信号采集系统的研究与设计［J］．电站系统工程，2008，24（3）：49．WANG Jin-ping，DENG Ai-dong，DING Ke-ke．Research on and Design of DSP-Based Turbine Vibration Signal Acquisition System［J］．Power System Engineering，2008，24（3）：49．（in Chinese）

［7］ 陈佳元，张秋菊，郁文凯．基于DCT的压缩机振动信号压缩方法研究［J］．压缩机技术，2009（4）：5．CHEN Jia-yuan，ZHANG Qiu-ju，YU Wen-kai．Research on Method for Vibration Signal Compression for a Compressor Based on DCT ［J］．Compressor Technology，2009（4）：5．（in Chinese）

［8］ 管博，胡劲松．基于DCT的旋转机械振动信号压缩方法研究［J］．风机技术，2007（3）：80．GUAN Bo，HU Jin-song．Research on Reduction Method for Vibration Signals of Rotating Machinery Based on DCT ［J］．Wind Turbine Technology，2007（3）：80．（in Chinese）

［9］ WU Q J，TIAN X B．Receiver Function Estimated by Wiener Filtering［J］．Earthquake Research in China，2003，17：387．

［10］ WILLIAM A G．Cyclic Wiener Filtering：Theory and Method［J］．IEEE Transaction On Communications，1993，41（1）：151．