黏土地层盾构隧道临界注浆压力计算及影响因素分析
叶 飞,苟长飞,毛家骅,杨鹏博,陈 治,贾 涛
(1.长安大学 公路学院,陕西 西安 710064;2.温州市铁路与轨道交通投资集团有限公司,浙江 温州 325000)
1 引 言
随着地下工程的快速发展,盾构工法以其施工安全、快速、对周围环境影响小等优点,广泛应用于城市地铁、公路、电力、通信、市政污水隧道施工中[1-2]。盾构推进过程中,管片拼装完成后,随着盾构向前推进,盾尾逐步脱离管片。由于盾构壳体具有一定厚度,壳体内径大于管片衬砌外径,且掘进过程中存在超挖等原因,盾尾脱离管片后在管片与地层之间便形成了盾尾间隙[3-4]。如不对盾尾间隙及时加以处置,土体将产生应力释放,周围地层产生变形,导致地表下沉过大、邻近建筑物倾斜等问题出现。因此,通常在盾构向前推进的同时从盾构机尾部注浆孔向管片壁后注入浆液,即盾尾注浆;或者在盾构推进一段距离后,通过预留在管片上的注浆孔向盾尾间隙注入浆液,即管片注浆。注浆技术虽然属于一种传统的工艺,但将其引入到盾构施工后仍存在不少亟待研究解决的问题。不管采用哪种注浆方式,注浆压力选择与控制都是壁后注浆效果是否良好的关键。注浆压力过大,可能引起管片局部或整体上浮、错台、开裂、压碎或其他形式的破坏、管片上的稳定土压力分布不均[4]、地表隆起、浆液从盾尾流入隧道内部等问题出现。反之,注浆压力过小,可能引起地表沉降超限,严重时会造成建筑物倾斜、开裂、倒塌、道路沉陷、影响交通。因此,壁后注浆过程中,必须合理选择注浆压力。
文献[2-3]建议注浆压力一般在0.1~0.3 MPa,并应参考覆盖土厚度、地下水压力及管片的强度进行设定。对钢管片来说,注浆压力为0.4~0.6 MPa时,首先会使管片环变形,然后造成主梁、肋板变形;对混凝土管片来说,封顶块螺栓在0.4 MPa左右有可能被剪断[2-3,5]。日本学者小泉淳指出,注浆压力应该由土压力、水压力、管片的强度及盾构的形式与使用材料特性进行综合判断,一般为0.1~0.3 MPa,建议取“孔隙水压力+0.2 MPa”[6]。日本土木学会建议,在考虑地层条件及施工方法的基础上来确定壁后注浆压力,管片设计中应对壁后注浆压力作用下管片进行验算。注浆压力一般以比泥水压、泥土压大0.05~0.10 MPa的压力作为标准[7],多采用0.2 MPa[8]。深圳地铁大东区间隧道中,注浆压力控制在0.3~0.5 MPa左右,以保证管片与围岩之间充填密实[9]。王江涛等[10]认为,注浆压力一般大于注浆口处静水压或土压0.1~0.2 MPa;并用此方法确定了南水北调中线穿黄工程泥水盾构在砂层中的注浆压力在0.4~0.6 MPa之间。国内外对盾构注浆压力与地表沉降量之间关系进行的研究表明,当注浆压力相当于隧道埋深处的地层应力时,对减少地层损失和地表沉降量效果最为显著。地铁隧道一般埋深在10~20 m之间,采用太沙基的土压力计算方法较为合理[11]。魏纲等[12]认为,注浆压力不能大于土体劈裂压力,理论上,注浆压力应略大于地层土压与水压之和,以达到对环向空隙的有效充填。所以,注浆压力一般控制在0.25~0.30 MPa,可取为地层土压与水压之和的1.10~1.15倍。宋天田等[13]在分析盾尾同步注浆作用机制的基础上,采用理论分析的方法,对同步注浆的注浆压力和注浆量进行了分析和研究,获得了在地层劈裂、泥水压力、上覆土3个主要影响因素下注浆压力的确定方法。叶飞等[14]将接头螺栓的抗剪效应与注浆对管片产生的压力结合起来,据接头螺栓的剪切破坏条件来控制注浆压力,即在求得注浆压力产生的螺栓剪应力前提下,要求该剪应力小于螺栓的许用剪应力,从而实现对注浆压力的控制。
徐方京等[15]在分析盾尾间隙引起软土地层移动的基础上,推导了维持黏土地层稳定的上、下临界注浆压力及最佳注浆压力;并以上海地铁1号线盾构为例,进行了实例验证。
从以上对注浆压力选择与控制的研究综述可以看出,目前注浆压力的选择多以经验为主,缺少现实可用的计算理论。鉴于此,笔者在前人研究的基础上,采用理论分析方法,推导黏土地层盾构施工时注浆压力的取值范围,即注浆压力的上、下临界值的计算式,进一步确定最佳注浆压力值。
2 注浆施工控制
盾构隧道壁后注浆施工中,通常压力控制和流量控制是同时进行的[2-3]。若按维持设定压力注浆,则注入流量不固定;若按维持设定流量注浆,则注入压力不固定。总之,单纯考虑注入流量或注入压力的方法均不理想,故常对两者进行综合控制,见图1。
注浆控制装置不仅能自动测量控制注入流量,同时还能自动控制注入压力。如果注入压力在设定范围内,则按照设定注入流量进行注入。如果注入流量比最佳注入流量大,则注入压力上升。注入压力超过压力设定范围时,自动注入流量设定器开始工作,注入流量和注入压力开始下降到设定范围。反之,若地层中出现尾隙以外的间隙使压力急剧减小,则注入流量自动上升,注浆压力开始恢复到设定范围。
由注浆控制过程可以看出,注浆压力设定是注浆控制的关键。因此,下文将推导注浆压力的上、下临界值理论公式,以得到注浆压力设定范围。

图1 注浆施工综合控制示意图Fig.1 Comprehensive operation chart of grouting process
3 临界注浆压力计算公式推导
3.1 基本假定
在自稳性较差的软黏土地层中进行盾构隧道施工时,管片脱离盾尾后很快会被周围土体包裹,很难形成厚度均匀的盾尾间隙。图2为黏性土地层中盾构壁后注浆的调查实例[5]。由图可以看出,黏性土中从管片注浆孔及时注浆,浆液将直接压密周围土体;在注浆压力较大时,对土体产生明显的劈裂效应。

图2 黏性土地层壁后注浆状况实例(单位:cm)Fig.2 A case of back-filled grouts diffusion in clay stratum (unit:cm)
为研究方便,根据已有关于压密注浆的研究[16-17],对图2的浆液扩散模式进行概化,提出以下基本假定:
(1)由于黏土渗透系数很小,因此,忽略浆液和土体交界面的渗透,假定壁后注浆先对周围土体产生压密效应,若注浆压力过大,则对周围土体产生劈裂效应。
(2)由于盾构隧道半径远大于压密注浆浆体扩张范围,忽略盾构管片的弧度效应,认为管片外壁为平面。
(3)将图2中浆体在土体中的不规则扩张概化为规则的半球形,则压密注浆过程就相当于在半无限土体中扩张一个半球形孔(见图3),在半球孔四周形成了一个应力影响区,该区由塑性区和弹性区组成(见图4)。

图3 压密注浆示意图Fig.3 Schematic of compaction grouting of shield tunnel
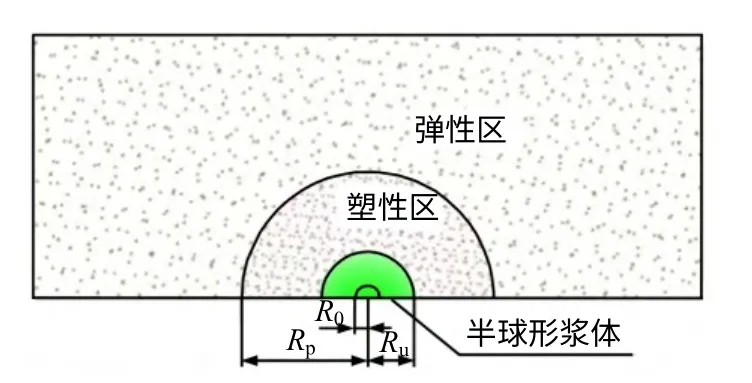
图4 球孔扩张应力区域Fig.4 Stress zone development during spherical expansion
(4)由于管片注浆孔一般为4~6个,在实际施工中只使用部分注浆孔进行注浆,且盾构隧道半径远大于压密注浆浆体扩张范围,当存在多个注浆孔同时注浆时,认为相互之间不产生影响。
3.2 弹塑性分析
设半球形浆体的初始半径为R0,扩张过程中的现时半径为Ru,相应的弹塑性交界面半径为Rp,Rp以外的土体仍然保持弹性状态。
根据弹塑性理论,球对称问题的平衡方程为
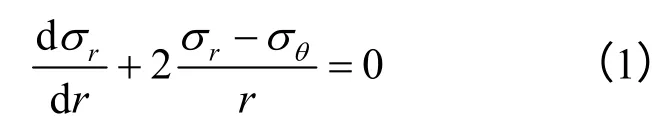
式中:σr为土体径向应力;σθ为土体环向应力。
几何方程为

弹性物理方程为

式中:εr为土体径向应变;ur为土体径向位移;ε为土体环向应变;Eθ为土体弹性模量;ν为土体泊松比。
边界条件为

式中:P为注浆压力;P0为注浆孔处的地下水压力。Mohr-Coulomb屈服准则为

随着注浆压力增大,浆体边缘的土体逐渐进入屈服。由式(1)~(5)可解出土体进入塑性状态的临界压力为

进一步解答,得到弹性区域(r≥Rp)应力和位移为

塑性区域(Ru≤r≤Rp)应力为
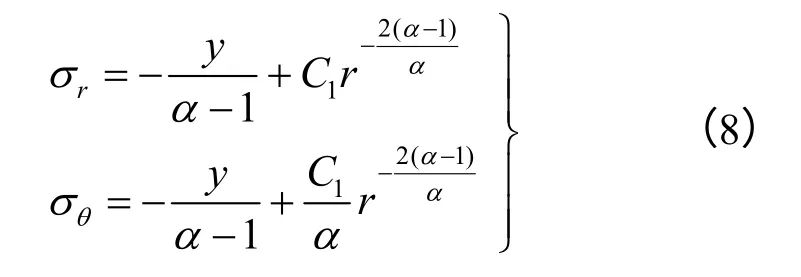
弹塑性交界面(r=Rp),径向应力为临界扩张压力Pp,即

将式(9)代入式(8),可得

将边界条件σr(Ru)=P 代入式(8),可得塑性区半径Rp、现时浆体半径Ru以及压力水平F 之间的关系为

式中:β为土体塑性区扩张半径与浆体扩张半径的比值。
可得浆体初始半径R0与现时半径Ru的关系式为

式中:ξ为浆体扩张率。
3.3 临界注浆压力
注浆压力过大可能导致浆体劈裂周围土体,扩张范围失去控制;导致管片结构破坏,或土体产生过大变形;也可能导致浆液通过盾尾密封刷渗透进入盾尾。注浆压力过小,不能平衡地下水压及土压,同样会造成周围土体变形过大。因此,下文分别以浆体无限扩张考虑劈裂效应,管片连接螺栓破坏考虑管片结构受力、盾尾刷窜浆,主、被动土压力公式考虑地层稳定性来推导壁后注浆压力上、下临界值计算式。
(1)由浆体无限扩张确定上临界值
注浆压力增大到一定程度以后,浆体将对周围土体产生劈裂效应。可见,浆体对土体的压密效应和劈裂效应间存在临界状态。压密状态中,整个半球形浆体半径在不断扩张;而劈裂状态中,浆体向局部破坏的土体劈裂流动。因此,本文将浆体无限扩张其半径趋于无穷时,作为压密与劈裂的临界状态。
浆体无限扩张时,扩张率ξ →∞,由式(13)可得

由式(14)可解出无限扩张时,土体塑性区扩张半径与浆体扩张半径比 βu1。将 βu1代入式(11)并结合式(12),用 Pu1替换P 可得浆体无限扩张模式下注浆压力上临界值 Pu1的计算式为

(2)由螺栓剪切破坏确定上临界值
注浆压力增大到一定程度时,浆体对管片产生的压力将使得连接螺栓承受过大的剪切力,极易使得螺栓被剪断。因此,可通过分析管片连接螺栓的剪切破坏来推导注浆压力上临界值。
浆体压密土体的过程中对管片产生的压力为

塑性土体对管片产生的压力为

压密注浆对管片产生的总压力为

当因注浆对管片的压力在个别管片背部集中时,会造成该受力管片与其临接管片之间有错动的趋势,当该荷载达到一定程度时,管片间可能会出现错台,甚至剪断连接螺栓[13]。根据文献[13],螺栓受到的最大剪应力计算式为

式中:lb为螺栓的有效长度;S为螺栓受到的等效剪力;λ为螺栓两剪力接触点之间的长度;rb为螺栓半径。
结合注浆对管片产生的压力计算式(18),此时螺栓受到的剪力为

式中:Ni为浆液扩散范围内连接螺栓数量(可取单块管片与周围临接管片的连接螺栓数),可得在一定注浆压力下,接头螺栓受到的剪应力为

将式(11)、(12)代入式(21),化简得

将式(22)代入式(13),可得关于β 的方程式为

将螺栓的许用剪应力代入式(23),解出考虑螺栓剪切破坏时,土体塑性区扩张半径与浆体扩张半径比 βu2。将 βu2代入式(11)并结合式(12),用Pu2替换P 可得浆体考虑螺栓剪切破坏时注浆压力上临界值Pu2的计算式为
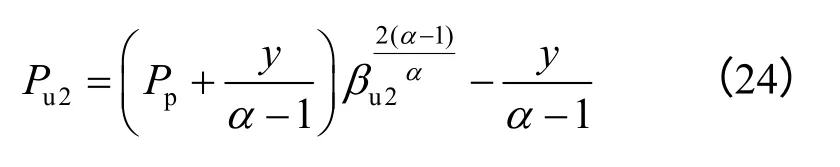
(3)由盾尾刷抗渗透性确定的上临界值
在注浆过程中,为保证浆液不击穿盾尾密封而造成窜浆,注浆压力应小于盾尾密封刷的抗渗透压力,即注浆压力上临界值应小于盾尾密封刷的抗渗透压力。因此,设盾尾密封刷的抗渗透压力为Pu3。
(4)由土体稳定性确定的上、下临界值
为保持地层稳定,注浆压力应大于注浆口处的主动土压力,且小于注浆孔处的被动土压力。因此,保持地层稳定的注浆压力上临界值可表示为

保持地层稳定的注浆压力下临界值可表示为

式中:γ为土体容重;h为注浆孔埋深。
由以上推导可以看出,盾构壁后注浆压力临界值与土体特性、管片结构、隧道埋深等因素有关。由浆体无限扩张和螺栓剪切破坏可确定注浆压力的上临界值,但公式中未直接考虑隧道埋深的影响。由土体稳定性可确定的注浆压力的上、下临界值,其所用主、被动土压力公式中考虑了隧道埋深的影响。下文通过一具体实例,来分析各因素对注浆压力临界值的影响。
4 实例分析
4.1 基本参数
某盾构隧道管片结构的螺栓长度lb=0.4 m,螺栓两剪力接触点之间的长度λ=0.01 m,螺栓半径rb=0.015 m,注浆孔临近的连接螺栓数量Ni=8,螺栓的许用剪应力[τ ]=175 MPa;土体的弹性模量E=2.85 MPa,黏聚力c=6 kPa,内摩擦角φ=18°,泊松比ν=0.2;注浆点处的地下水压力P0=50 kPa,注浆孔半径R0=2.5 cm;盾尾密封刷的抗渗透压力为0.8 MPa。
4.2 土体特性对注浆压力上临界值的影响
(1)不同弹性模量
假定土体弹性模量在2.85~6.85 MPa之间,其余参数与基本参数相同。应用文中公式,分别计算不同土体黏聚力下考虑浆体无限扩张和螺栓剪切破坏时注浆压力上临界值,计算结果如图5所示。
由图可以看出,考虑浆体无限扩张和螺栓剪切破坏时的注浆压力上临界值均随土体弹性模量的增大而增大;考虑浆体无限扩张时的注浆压力上临界值始终大于考虑螺栓剪切破坏时的上临界值,两者的差值在0.023~0.052 MPa之间,且随着土体弹性模量的增大而增大。可见,注浆压力上临界值受土体弹性模量影响显著。

图5 不同土体弹性模量下注浆压力上临界值Fig.5 The upper critical limits of grouting pressure for different elastic moduli
(2)不同土体黏聚力
假定土体黏聚力c 在6~14 kPa之间,其余参数与基本参数相同。应用文中公式,分别计算不同土体黏聚力下考虑浆体无限扩张和螺栓剪切破坏时注浆压力上临界值,计算结果如图6所示。
由图可以看出,考虑浆体无限扩张和螺栓剪切破坏时的注浆压力上临界值均随土体黏聚力的增大而增长,且增长曲线近似呈平行直线;考虑浆体无限扩张时的注浆压力上临界值始终大于考虑螺栓剪切破坏时的上临界值,其差值在23~27 kPa之间。可见,注浆压力上临界值受土体黏聚力影响显著。
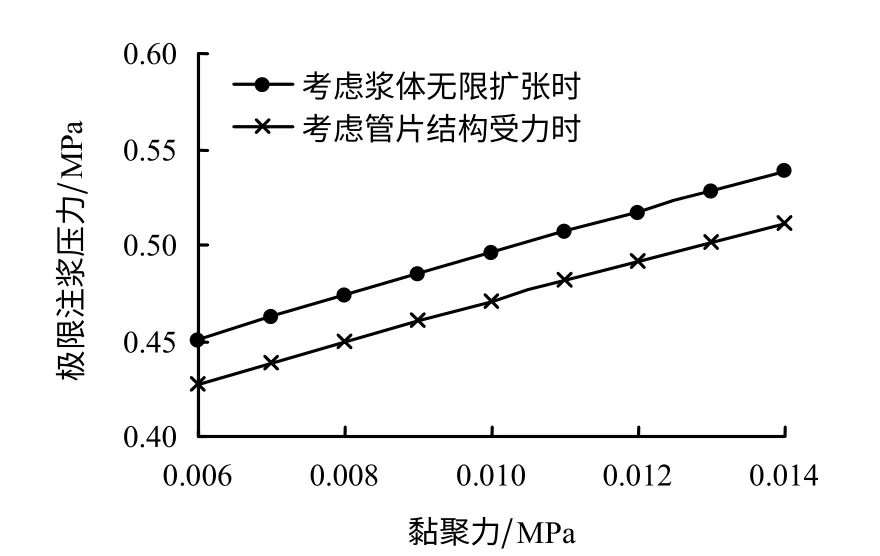
图6 不同黏聚力下注浆压力上临界值Fig.6 The upper critical limits of grouting pressure for different cohesions
(3)不同土体内摩擦角
假定土体的内摩擦角φ 在18°~22°之间,其余参数与基本参数相同。应用文中公式,分别计算不同土体内摩擦角下考虑浆体无限扩张和螺栓剪切破坏时注浆压力上临界值,计算结果如图7所示。
由图可以看出,考虑浆体无限扩张和螺栓剪切破坏时的注浆压力上临界值均随土体内摩擦角的增大而增长,且曲线近似呈平行直线;考虑浆体无限扩张时的注浆压力上临界值始终大于考虑螺栓剪切破坏时的上临界值,其差值在23~28 kPa之间。可见,注浆压力上临界值受土体内摩擦角影响显著。

图7 不同内摩擦角下注浆压力上临界值Fig.7 The upper critical limits of grouting pressure for different internal friction angles
(4)不同地下水压
假定土体注浆孔处地下水压在50~90 kPa之间,其余参数与基本参数相同。应用文中公式,分别计算不同地下水压下考虑浆体无限扩张和螺栓剪切破坏时注浆压力上临界值,计算结果如图8所示。
由图可以看出,考虑浆体无限扩张和螺栓剪切破坏时的注浆压力上临界值均随注浆孔处地下水压的增大而增长,且曲线近似呈平行直线;考虑浆体无限扩张时的注浆压力上临界值始终大于考虑螺栓剪切破坏时的上临界值,其差值在4~23 kPa之间,且随地下水压的增大而增大。可见,注浆压力上临界值受注浆孔处地下水压的影响显著。
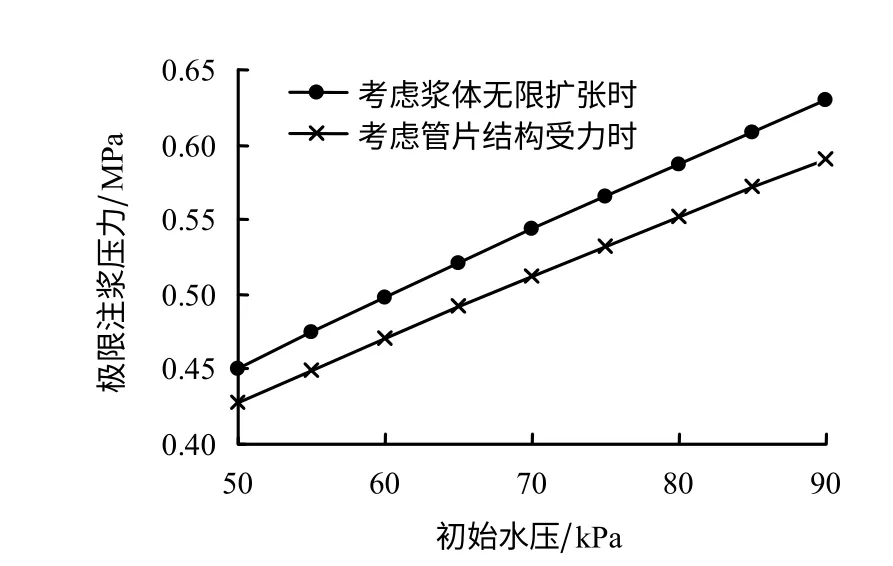
图8 不同地下水压下注浆压力上临界值Fig.8 The upper critical limits of grouting pressure at different pore water pressure
通过对图5~8的分析可知,盾构隧道壁后注浆压力上临界值受土体弹性模量、黏聚力、内摩擦角、注浆孔处地下水压,以及管片结构性能等的共同影响。壁后注浆压力过大时,管片结构可能因螺栓被剪断而破坏。因此,在控制注浆压力时,应该综合考虑土体性质和管片结构性能。
4.3 隧道埋深对注浆压力上、下临界值的影响
上文提到,由浆体无限扩张和螺栓剪切破坏确定的注浆压力的上临界值计算式中未直接考虑隧道埋深的影响,而由土体稳定性确定的注浆压力上、下临界值计算式(式(25)、(26))中考虑了隧道埋深的影响。因此,本节应用式(25)、(26)分析隧道埋深对注浆压力上、下临界值的影响。
假定注浆孔处埋深在6~22 m之间,其余参数与基本参数相同。应用文中公式,分别计算考虑隧道埋深的注浆压力上、下临界值,计算结果如图9所示。
由图可以看出,注浆压力上、下临界值均随注浆孔处埋深的加深而近似呈直线增大;上、下临界值之间的差距也随注浆孔处埋深的加深而增大。可见,随着隧道埋深的变浅,注浆压力可选范围逐渐变小。因此,在浅埋条件下,应特别注意注浆压力控制。
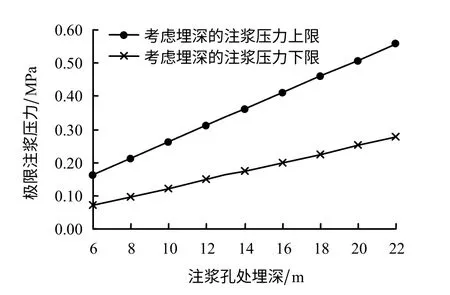
图9 不同埋深下临界注浆压力Fig.9 Critical grouting pressure at different depths
5 最优注浆压力确定
由实例分析可以看出,注浆压力上临界值在考虑浆体无限扩散、螺栓剪切破坏、隧道埋深、盾尾刷窜浆4种情况下的计算结果不尽相同。为安全起见,应以四者中最小值作为最终的注浆压力上临界值:

注浆压力下临界值为

注浆压力上、下临界值确定以后,将上、下临界值分别除以及乘以一个安全系数n(n >1),便可得到最优注浆压力。

由式(29)可得安全系数为

最优注浆压力为

将3.1节中基本参数代入文中公式,注浆孔处的埋深取为20 m,可求出注浆压力上临界值为

注浆压力下临界值为:Pmin=Pma=0.251 MPa

最优注浆压力为

可见,在3.1节基本参数下,注浆压力理论上应维持在0.251~0.428 MPa范围内;为安全起见,应尽量接近于最优注浆压力0.326 MPa。
6 结 论
(1)通过理论分析得到了考虑浆体无限扩张、螺栓剪切破坏、盾尾窜浆的注浆压力上临界值计算式,以及考虑隧道埋深的注浆压力上、下临界值计算式。在实例分析中,进一步推导出了基于安全系数考虑的最优注浆压力的计算式,为盾构隧道壁后注浆施工提供了偏于安全的注浆压力参考值。
(2)临界注浆压力及由此得到的最优注浆压力与土体弹性模量、黏聚力、内摩擦角、初始地下水压力,管片结构性能以及隧道埋深等因素有关,应综合考虑土体特性、管片结构性能和隧道埋深来选择合适的注浆压力。
(3)注浆压力上临界值随着土体弹性模量、黏聚力、内摩擦角、初始地下水压力及隧道埋深的增大而增大;注浆压力下临界值随着隧道埋深的增大而增大。
(4)注浆压力过大时,管片结构可能因螺栓被剪断而破坏;注浆压力过小时,土体可能因失去稳定支撑而产生较大变形。因此,注浆过程中应使注浆压力尽量接近最优注浆压力,不得超出临界注浆压力所限定的范围。
[1]张厚美.盾构隧道的理论研究与施工实践[M].北京:中国建筑工业出版社,2010.
[2]张凤祥,朱合华,傅德明.盾构隧道[M].北京:人民交通出版社,2004.
[3]张凤祥,傅德明,杨国祥,等.盾构隧道施工手册[M].北京:人民交通出版社,2005.
[4]李雪,周顺华,王培鑫,等.盾构隧道实测土压力分布规律及影响因素研究[J].岩土力学,2014,35(增刊2):453-459.LI Xue,ZHOU Shun-hua,WANG Pei-xin,et al.Study of distribution law of earth pressure acting on shield tunnel lining based on in-situ data[J].Rock and Soil Mechanics,2014,35(Supp.2):453-459.
[5]伊旅超,朱振宏,李玉珍,等.日本隧道盾构新技术[M].武汉:华中理工大学出版社,1999.
[6][日]地盘工学会.盾构法的调查·设计·施工[M].牛清山,陈凤英,徐华,译.北京:中国建筑工业出版社,2008.
[7][日]土木学会.盾构隧道管片设计——从容许应力设计法到极限状态设计法[M].管林星,译.北京:中国建筑工业出版社,2012.
[8][日]土木学会.隧道标准规范[盾构篇]及解说J(2006年制定)[M].朱伟,译.北京:中国建筑工业出版社,2011.
[9]陈湘生,李兴高.复杂环境下盾构下穿运营隧道综合技术[M].北京:中国铁道出版社,2011.
[10]王江涛,陈建军,吴庆红,等.南水北调中线穿黄工程泥水盾构施工技术[M].郑州:黄河水利出版社,2010.
[11]何炬,杨有海,陈达.深圳地铁盾构施工注浆机理与参数分析[J].低温建筑技术,2009,(10):108-109.HE Ju,YANG You-hai,CHEN Da.Grouting mechanism and parameter analysis of shield construction in Shenzhen Subway[J].Low Temperature Building Technology,2009,(10):108-109.
[12]魏纲,魏新江,洪杰.盾构隧道壁后注浆机理及其对周边环境的影响[J].防灾减灾工程学报,2010,30(9):299-304.WEI Gang,WEI Xin-jiang,HONG Jie.The backfill grouting mechanism and impact to surrounding environment in shield tunnel[J].Journal of Disaster Prevention and Mitigation Engineering,2010,30(9):299-304.
[13]宋天田,周顺华,徐润泽.盾构隧道盾尾同步注浆机理与注浆参数的确定[J].地下空间与工程学报,2007,4(1):130-133.SONG Tian-tian,ZHOU Shun-hua,XU Run-ze.Mechanism and determination of parameters of synchronous grouting in shield tunneling[J].Chinese Journal of Underground Space and Engineering,2007,4(1):130-133.
[14]叶飞,朱合华,丁文其.基于螺栓接头受力性能的盾尾注浆压力控制[J].同济大学学报(自然科学版),2009,37(3):312-316.YE Fei,ZHU He-hua,DING Wen-qi.Pressure control analysis based on mechanical properties of bolts during grouting at shield tail[J].Journal of Tongji University(Natural Science),2009,37(3):312-316.
[15]徐方京,侯学渊.盾尾间隙引起地层移动的机理及注浆方法分析[J].地下工程与隧道,1993,(3):12-16,20.
[16]汪鹏程,朱向荣,方鹏飞.考虑土应变软化及剪胀特性的大应变球孔扩张的问题[J].水利学报,2004,(9):78-82,87.WANG Peng-cheng,ZHU Xiang-rong,FANG Peng-fei.Expansion of large strain spherical cavity in soil in consideration of dilation and strain softening[J].Journal of Hydraulic Engineering,2004,(9):78-82,87.
[17]汪鹏程,张红亚.弹塑脆性岩土材料中球形孔大应变扩张分析[J].安徽建筑工业学院学报(自然科学版),2008,16(2):17-22.WANG Peng-cheng,ZHANG Hong-ya.Analysis of spherical cavities expansion in elastoplastic-brittle[J].Journal of Anhui Institute of Architecture &Industry,2008,16(2):17-22.

