基于潮流熵的输电线路差异化防雷改造顺序研究

周 凯，张富春

(国网冀北电力有限公司秦皇岛供电公司，河北 秦皇岛 066000)

基于潮流熵的输电线路差异化防雷改造顺序研究

周 凯，张富春

(国网冀北电力有限公司秦皇岛供电公司，河北 秦皇岛 066000)

为了提高输电线路差异化防雷改造工作的效率，有效降低雷击故障对电网可靠性的负面影响，提出依据输电线路的重要度对其进行有序差异化防雷改造。针对雷电故障导致输电线路跳闸退出运行后线路潮流熵的变化特点，结合熵理论及其在电力系统中的应用，定义潮流转移熵，建立基于潮流转移熵的输电线路重要度评估模型。为加快计算速度，采用直流潮流转移分布因子法计算输电线路上的潮流变化。最后，通过对IEEE 3机9节点系统的算例测试，验证了所提方法的可靠性和正确性。

电力系统;输电线路;潮流转移熵;潮流转移因子;有序差异化防雷改造

0 引言

近年来，随着电网的快速发展和强对流天气的增多，雷害故障频发。在我国超过50%的电力系统故障是由雷击引起的，2004年南方电网500 kV线路共发生故障62起，其中雷击故障54次，占总故障的87.1%;2008年南方电网110 kV及以上输电线路共计跳闸2 599次，其中雷击跳闸1 588次，占总跳闸数的61.1%［1］，居各类线路跳闸原因中的第一位。输电线路雷击故障不仅造成输电设备损坏，而且由雷击引发的线路相继故障还威胁电网的安全可靠运行，严重影响着社会经济的发展。因此，输电线路防雷改造的相关研究具有重要的现实意义。

目前，输变电系统雷电防护主要以降低雷电跳闸率为目标［2，3］。文献 ［4］提出了输电线路差异化防雷计算，该方法主要基于杆塔雷击闪络概率进行风险等级评估，主要是以雷击跳闸率为参考确定雷击闪络风险评估标准。文献 ［5］提出了综合考虑技术经济性指标的输电线路防雷措施评估方法，该方法综合考虑了雷击跳闸率的降低效果、雷电防护工程的费用、雷电防护改造的目标以及难易程度等因素，但是该方法仍然侧重以降低雷击跳闸率为重要参考，选定最优防雷改造措施。

然而，雷击跳闸率指标是以电压等级为依据进行区分，随着电网规模不断扩大、运行方式多样和复杂程度不断增加，这种传统的对电压等级相同而运行状态和重要性不同的输电线路，按照一定顺序采用相同雷电防护措施的做法显然不科学且存在一定的盲目性，可能造成重点线路雷电防护滞后且保护水平相对不足，而一般线路雷电防护置前且相对过剩的后果。因此，需要从电网安全性角度考虑，对输电线路的重要度进行评估，以评估结果指导输电线路差异化防雷改造工作的有序进行，确定“有选择、有侧重、有针对、有差别”的输电线路防雷工作策略。

当前，依据输电线路在电网中的重要度进行有序差异化防雷改造的研究还很少。由此，本文针对处于雷电多发地带需进行雷电防护改造的线路，以线路遭受雷击断线后潮流转移特性，结合潮流熵理论［6］，评估线路的重要程度，评估结果用于指导输电线路的有序差异化防雷改造工作。

1 熵理论及其在电力系统中的应用

电力系统是一个非线性复杂的能量平衡系统，可采用潮流分布的熵变过程衡量系统内部的动态稳定性能。因此，基于熵理论［8，9］

式中:δi为电力系统元件i的潮流分布率;N为电力系统的元件总数。

电力系统潮流熵的物理意义为:系统在特定运行状态下，对系统内部潮流分布均匀程度的度量，潮流熵值越大，表明能量分布越均匀、系统越稳定。当系统中各元件分摊的潮流相同，即潮流分布率均为δi=1/N，在这种理想条件下，系统的潮流熵达到最大值lnN，此时的系统也是最稳定的。

电力系统是一个非线性的、具有复杂网络结构的系统，本身具有一定的自组织特性，还受人为对其施加的安全控制、继电保护等约束，对外界的冲击扰动具有一定的抵抗能力，通过自我调节，往往能够从一种平衡状态过渡到另一种平衡状态，保持一种动态平衡。当电力系统处于潮流较均匀分布的平衡状态时，对外界扰动具有较强的抵抗力，而元件故障停运等行为，是破坏系统稳定的一种潮流冲击，增加了系统的不确定性，相当于给系统注入了潮流负熵;而系统自身的组织特性以及安全约束条件，会消除或削弱扰动的影响，相当于给系统注入了潮流正熵;当潮流正熵足以抵消潮流负熵时，系统会从原来的平衡状态过渡到一个新的平衡状态，仍可维持稳定;而当潮流正熵不足以抵消潮流负熵时，系统将失去平衡状态，趋于崩溃。

电力系统中的输电线路因故障而退出运行时，潮流会发生转移和重新分布，是对系统的一次潮流冲击，显然处于不同位置以及运行状态的输电线路的故障停运，对系统的潮流冲击大小是不同的，可将熵理论引入到电力系统中评估输电线路重要度。本文主要侧重于输电线路由于雷击故障退出运行后，会对系统中剩余线路产生潮流冲击，以线路故障退出运行对系统造成危害的大小，评估输电线路的重要度，用于指导输电线路差异化防雷改造工作的有序进行。

2 基于潮流熵的线路重要度评估模型

传统输电线路重要度指标定义为:当输电线路故障或停运给系统带来的影响。目前，对输电线路重要度指标的研究通常基于复杂网络理论，以线路被电源到负荷节点所经历的最短路径经过的次数定义线路介数，并通过算例验证得出高介数线路在电网中占有重要位置，具有较高的重要度［10～13］。但是，潮流在电网中不仅沿最短路径传输，而是要满足基尔霍夫定律，经多条路径传输，显然功率沿最短路径传输的假设不符合物理实际［14］。文献 ［15］对线路介数进一步完善，提出电气介数作为衡量线路重要度的指标，该指标虽然克服了母线间潮流只沿最短路径流动的不足，但是仅仅从静态角度考虑线路合断对系统造成的影响，不能体现线路退出运行后的动态过程。而潮流熵理论恰恰弥补了这个不足，考虑了线路由于故障退出运行后，潮流发生转移和重新分布对系统造成的影响。

当系统中线路Li由于故障退出运行后，该条线路传输的功率会经由其他路径发生转移，引起线路Lj传输功率的变化量为ΔPij:

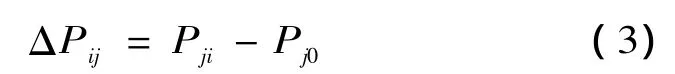
式中:Pi0为线路Li退出运行前线路Lj传输的功率;Pji为线路Li退出运行后线路Lj传输的功率;ΔPJI为线路Lj传输功率的变化量，反映了线路Li退出运行对线路Lj的潮流转移冲击。

定义线路Li退出运行对线路Lj的潮流转移冲击率为δji:

对于SCV温度串级控制系统，根据前述分析，其数学模型可以近似地以一阶惯性环节来逼近，考虑SCV水浴系统的过程特性[10-11]，通过测量系统的阶跃响应曲线，利用切线法，求得主控对象NG出口温度和副控对象SCV水浴温度的数学模型分别为:

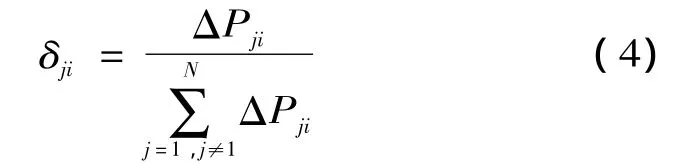
定义线路Li的潮流转移熵为HTi:

定义基于线路潮流转移熵的线路Li的重要度指标为HTi:

式中:Pi为线路Li上的传输功率。

当输电线路因故障而退出运行时，其传输的功率越大，对系统中剩余线路的潮流冲击越大;潮流转移熵越小，表明因线路故障退出运行引起的系统潮流转移冲击，主要集中在少数几条线路上，更容易引起其它线路过负荷跳闸而相继退出运行，发生后果极其严重的连锁故障。因此，该线路重要度指标具有明确的物理意义。

3 基于直流的支路潮流转移分布因子

计算输电线路重要度指标的关键元素为ΔPji，采用交流潮流算法计算ΔPji虽然结果精确，但是计算量较大，占用内存较多，计算速度较慢。当较多的输电线路需要雷电防护改造，而又尽量在雷雨季节到来之前完成改造工作，这就需要尽量减少计算工作量，提高计算速度，以满足实际需求。采用直流潮流转移因子法计算ΔPji，虽然在精度方面不如交流潮流法，误差为10%左右，却能够简化计算过程，减少计算工作量，提高潮流计算速度［16］。通过后面的算例验证，对比交流潮流计算结果，直流潮流计算存在的误差不影响输电线路重要度排序，根据实际需要，该误差是可以接受的。

当线路Li由于故障退出运行后，线路Lj承担线路Li转移的潮流比例为潮流转移因子λji:

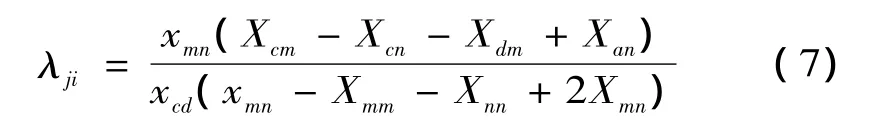
式中:m、n和c、d分别为线路Li与线路Lj的首末节点;xmn为线路Li的电抗;xcd为线路Lj的电抗;Xda、Xca、Xcm、Xnn等分别为基态时网络节点阻抗矩阵中的对应元素。

基于潮流转移因子，计算线路Li退出运行后引起线路Lj传输功率的变化量ΔPji:

4 算例分析

为验证本文所提方法的有效性和正确性，将IEEE 3机9节点系统作为算例系统，其具体接线图如图1所示。该算例系统包含3台发电机，3个负荷节点和9条输电线路。

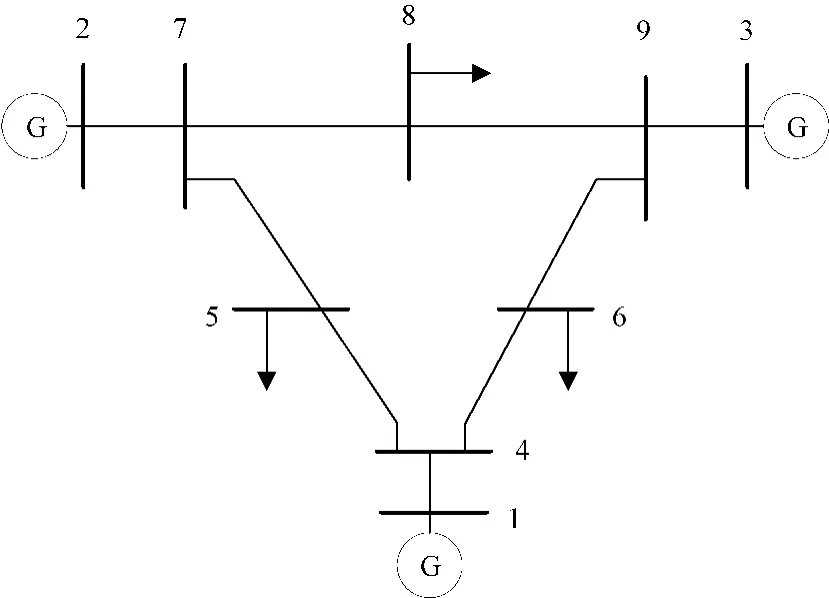
图1 IEEE 3机9节点系统

假设IEEE 3机9节点系统的各条输电线路处于雷电多发地带，需进行雷电防护改造工作。采用本文提出的基于潮流熵的输电线路有序差异化防雷改造，应逐条计算输电线路因雷击故障而退出运行后的潮流转移熵，分别以直流潮流法和交流潮流法计算各条线路切除后的潮流转移熵，将归一化指标由大到小排序，并将结果列于表1。

由表 1 可得出，L2－7、L5－7和 L3－9等输电线路的重要度指标较大，即这些线路由雷击故障退出运行后，将对系统带来较严重的后果，在有限的时间和经济条件下，应优先对这些线路进行雷电防护改造，并加强雷电防护措施;而对于L4－5、L4－6和L8－9等输电线路的重要度指标较小，在较多的输电线路需要雷电防护改造，且资金有限、时间较紧的情况下，可以适当延期对这些线路的雷电防护改造。即使这些线路由雷击故障退出运行，可能也不会给系统造成致命的创伤，甚至系统能够消纳这次扰动给系统带来的能量负熵。综上所述，本文提出的基于潮流熵的输电线路有序差异化防雷改造，对有条不紊地开展雷电防护改造工作具有重要的指导意义。图1所示为IEEE 3机9节点系统中的各条输电线路的重要度分布图。

表1 基于潮流转移熵的线路重要度排序

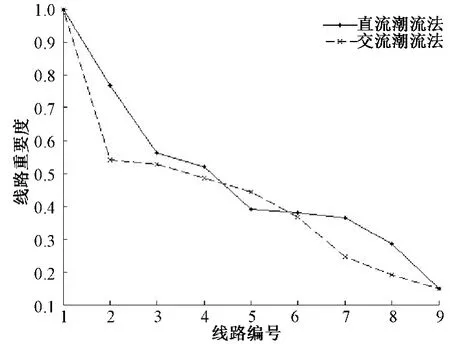
图2 基于潮流熵的线路重要度分布图

由表1和图2可知，采用直流潮流法计算输电线路重要度指标与交流潮流法的计算结果虽然存在差异，但是输电线路的重要度的排列次序是一致的，对指导输电线路差异化防雷改造工作的指导意义相同。因此，采用直流潮流进行输电线路重要度指标计算的方法是可行的。

5 结论

本文提出了基于潮流熵的输电线路差异化防雷改造顺序的新方法，该方法主要考虑处于多雷电地带的输电线路，需进行雷电防护工作，针对雷电防护工作量大、时间有限等特点，从输电线路由雷击故障退出运行给系统带来的后果严重度角度，评估出比较重要的输电线路，优先对这些线路开展雷电防护工作，并加强雷电防护措施。该方法优化了传统的输电线路雷电防护方法，能够显著提高输电线路差异化防雷改造工作的效率，有效降低雷击故障对电网可靠性的负面影响。下一步将研究考虑雷电故障概率，结合雷电后果，应用风险理论综合评估线路的重要度，提出更加准确全面的评估指标。

［1］南方电网公司．南方电网线路运行统计报告 ［R］．广州:南方电网公司，2008．

［2］国网电力科学研究院，电网雷害风险评估技术研究［R］．武汉:国网电力科学研究院，2011．

［3］张瑞．输电线路雷击闪络风险评估研究 ［D］．武汉:武汉大学，2009:42－49．

［4］阮羚，谷山强，赵淳，等．鄂西三峡地区220kV线路差异化防雷技术与策略 ［J］．高电压技术，2012，38(1):157－166．

［5］赵淳，阮江军，李晓岚，等．输电线路综合防雷措施技术经济性评估 ［J］．高电压技术，2011，37(2):290－297．

［6］曹一家，张宇栋，林辉，等．基于同配性的电力系统自组织临界性识别 ［J］．电力自动化设备，2013，33(7):6－11，18．

［7］李勇，刘俊勇，刘晓宇，等．基于潮流熵的电网连锁故障传播元件的脆弱性评估 ［J］．电力系统自动化，2012，36(19):11－16．

［8］梁才，刘文颖，温志伟，等．电网组织结构对其自组织临界性的影响 ［J］．电力系统保护与控制，2010，38(20):6－11．

［9］刘耀年，术茜，康科飞，等．基于电抗加权介数指标的电网脆弱线路识别 ［J］．电力系统保护与控制，2011，39(23):89－92．

［10］曹一家，陈晓刚，孙可．基于复杂网络理论的大型电力系统脆弱线路辨识 ［J］．电力自动化设备，2006，26(12):1－5．

［11］何俊，庞松龄，禹冰，等．基于容量介数指标的电网脆弱性线路识别 ［J］．电力系统保护与控制，2013，41(8):30－35．

［12］王仁伟，张友刚，杨阳，等．基于电气介数的复杂电网脆弱线路辨识 ［J］．电力系统保护与控制，2014，40(20):1－6．

［13］苏慧玲，李扬．基于准稳态功率转移分布因子的电力系统复杂网络特性分析［J］．电力自动化设备，2013，33(9):47－53．

［14］Bompard E，Napoli R，Xue F．Extended approach for theassessment of structural vulnerability in transmission networks［J］．IET Generation Transmission ＆ Distribution，2010，4(6):716－724．

［15］徐林，王秀丽，王锡凡．电气介数及其在电力系统关键线路识别中的应用 ［J］．中国电机工程学报，2010，30(1):33－39．

［16］程临燕，张保会，郝志国，等．基于线路功率组成的关键输电断面快速搜索 ［J］．中国电机工程学报，2010，30(10):50－56．

Research on Differentiated Lightning Protection Renovation Sequence of Transmission Lines Based on Power Flow Entropy

Zhou Kai，Zhang Fuchun

(State Grid Qinhuangdao Electric Power Company，Qinhuangdao 066000，China)

In order to improve the efficiency of differentiated lightning protection for transmission lines，and effectively reduce the negative impact of a lightning strike fault on the power grid reliability，research on sequence of differentiated lightning protection renovation of transmission lines is proposed based on the importance of transmission lines．According to the change of power flow entropy after line fault caused by lightning，and entropy theory and its application in power systems，power flow transfer entropy was first defined and then used as a basis in the establishment of an assessment model of the importance of lines．To speed up the computing，DC current transfer factor was untilized to calculate the change of power flow．Finally，the example test results of IEEE 3-machine 9-bus verify the reliability and validity of the proposed algorithm．

electric power systems;transmission lines;power flow transfer entropy;power flow transfer factor;renovation of ordered and differentiated lighting protection

TM726

A

10.3969/j.issn.1672-0792.2015.11.007

2015－07－06。

周凯 (1980-)，男，工程师，研究方向为电力工程技术，E-mail:Zaochenzhaoyang@126.com。