基于小波分解和SVM的滚动轴承故障程度研究

尤晓菲，何 青

(华北电力大学能源动力与机械工程学院，北京 102206)

基于小波分解和SVM的滚动轴承故障程度研究

尤晓菲，何 青

(华北电力大学能源动力与机械工程学院，北京 102206)

提出一种采用小波分解和支持向量机 (Support Vector Machine，简称SVM)提取故障特征的滚动轴承故障诊断方法。首先对原始振动信号进行小波降噪处理，以减小误差，然后进行小波分解，并利用分解得到的小波重构系数计算其能量特征，归一化后作为特征向量，输入SVM中进行故障诊断。实验结果表明，所提出的方法能有效地提取出故障特征，并且具有较高的故障诊断准确率，能准确地区分出滚动轴承不同故障的严重程度。

滚动轴承;故障诊断;小波分解;支持向量机

0 引言

滚动轴承摩擦阻力小，润滑简便，更换容易，因此，旋转机械中应用最为广泛的零件就是滚动轴承，同时也成了易损零件。若接触应力在其工作面上长期反复作用，疲劳、裂纹、压痕等故障就极易出现在滚动轴承之中，严重时甚至会导致轴承断裂，造成事故，产生巨大的经济损失［1，2］。据统计，在旋转机械设备故障中，约有30%的故障是由轴承损坏引起的［3］。因此，为了避免事故的发生，减少经济损失，对滚动轴承的状态监测和故障诊断技术的研究就显得尤为重要，也是研究的热点。

当滚动轴承发生故障时，其振动信号会表现出非平稳、非线性的特征［4］。传统的信号处理方法，如幅值域分析法，虽然有着简单直观，计算方便的独特优势，但是却无法得到任何频域特征。而傅里叶变换虽然能把时域信号转换到频域信号进行分析，克服了一些不足，但是对非平稳、非线性信号的处理仍缺乏局域性信息，不能实现对信号的局部分析。相比而言，小波变换则是一种信号的时间—尺度分析方法，还具有多分辨率分析的特点，而且在时频两域都具有表征信号局部特征的能力［5］，因此得到了广泛应用。

本文提出了一种利用小波变换实现滚动轴承原始振动信号的降噪与分解，而后根据小波重构系数计算出其能量特征，归一化后再输入支持向量机 (Support Vector Machine，SVM)中进行滚动轴承不同故障程度的分类识别方法，并且通过实验结果证明了该方法的有效性。

1 小波分解与特征提取

1.1 小波分解方法

小波是一种常用的信号处理方法，广泛应用于信号处理领域中。它的每一次分解过程，都是将信号分解成为近似部分和细节部分，即近似信号和细节信号，以便于做进一步的分析处理［6］。而在这两部分中，近似信号是最能反映信号本质信息的。小波分解实质上就相当于一个信号分别通过低通和高通滤波器，随后的每次分解都只针对低频部分，即近似部分，进行进一步的分解，而高频部分不予考虑。如图1所示，S是原信号，对其进行了三层分解，而每层的A代表信号的低频部分，是近似信号，D则代表信号的高频部分，为细节信号，分解后与原信号关系可表示为S=A3+D3+D2+D1［7］。

图1 小波分解

如果给出有限的能量函数ψ(t)，即ψ(t)∈L2(R)，当其傅里叶变换^ψ(ω)满足以下的容许条件:

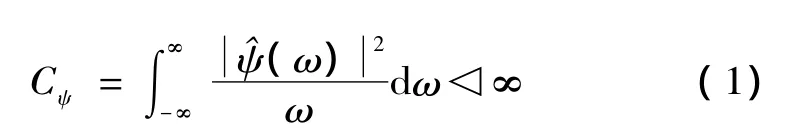
则ψ(t)称为母小波，并且可以伸缩和平移。ψ(t)这种伸缩和平移的特点可以描述为:

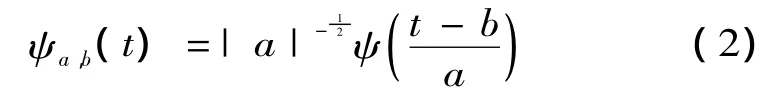
式中:a为伸缩因子，也称为尺度因子;b则称为平移因子。由于a和b取值连续变化，因此称ψa，b(t)为连续小波基函数，是由上述同一母函数ψ(t)经伸缩和平移后得到的一组函数系列。

将ψ(t)∈L2(R)空间的任意函数f(t)在式(2)的小波基下进行展开，则随机函数f(t)的连续小波变换式为

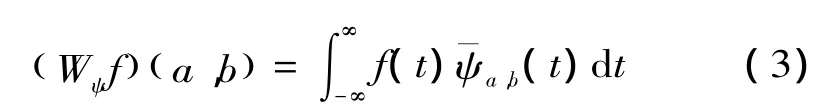
式中:(Wψf)(a，b)为小波变换系数。小波变换在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分则相反。低频信号变化缓慢，而高频信号改变迅速，这就是小波变换优于传统傅里叶变换之处［8］。

对式 (3)中的a，b做离散化，就可以得到离散小波分析，离散小波函数:

由式 (5)可见，离散小波变换是从集中于某个区间的基本函数开始，以规定的步长，向左或向右移动的基本波形，并用尺度因子扩张或压缩，由此来构造基函数系，进而产生一系列小波［9］。

小波重构公式:

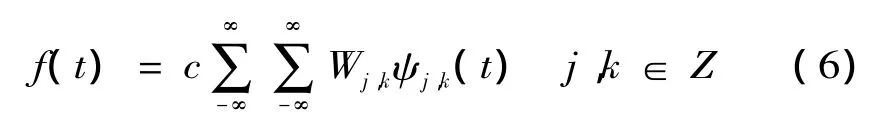
式中:c为与信号无关的参数。

1.2 能量特征提取

假设离散小波对信号f(t)的L层分解可以表示为

则可以将帕塞瓦尔能量EP定义如下:

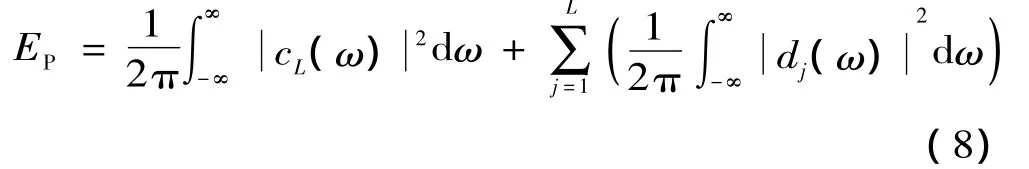
由帕塞瓦尔定理可知，帕塞瓦尔能量表明时间域中的总能量等于频谱域中的总能量，因此考虑信号的能量问题时，不仅可以在时域或频域单一范围内使用，也可以在时域和频域中交替使用［10］。

则利用帕塞瓦尔能量提取小波分解后各层能量特征E的方法如下:

2 支持向量机

支持向量机是Vapnik在统计学理论的基础上提出的一种新的机器学习方法［11］。SVM不同于神经网络等对样本数量的要求，是一种小样本学习方法，与现有的统计方法也有很大的区别，很少涉及概率测度及大数定律等内容，可以大大地简化一般的分类和回归问题。基于其在非线性即高维模式识别中的独特优点［12］，SVM这种方法经常在故障诊断时为人们所利用。

图2为SVM在两类分类下的利用情况。共有两类数据点，设圆圈代表正类，方形代表负类。SVM的作用是寻找一个最佳位置给线性边界H，使图中所示的间隔‖ω‖－2最大，得到最佳分类结果。图中H1和H2上的数据点就是支持向量。

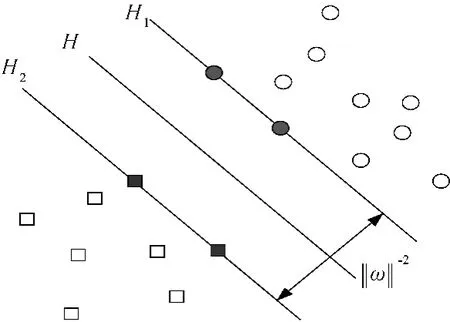
图2 SVM分类

设xi(i=1，2，…，M)为输入数据，其中M为样本数。样本包括两类，一类为正类，标签为yi=1，一类为负类，标签为yi=－1。分类面方程如下所示:

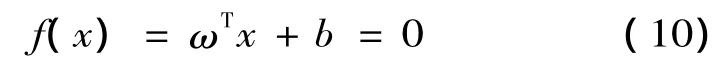
其中，M维向量ω和标量b的值决定了分类超平面的位置。

通过下式可以得到最优超平面:

式中:ξi表示噪声样本点与间隔之间的距离;C代表对错分样本的惩罚程度。

在解决滚动轴承的故障模式识别问题时，往往需要构造多类分类器。根据文献 ［13］，选取“一对一”的构造方法，其具体步骤是:将一个k类问题两两组合，然后针对每个组合构造一个SVM模型，此时每个SVM模型都为上述的二分类问题，一共会有k(k－1)/2个，最后对下式求解:

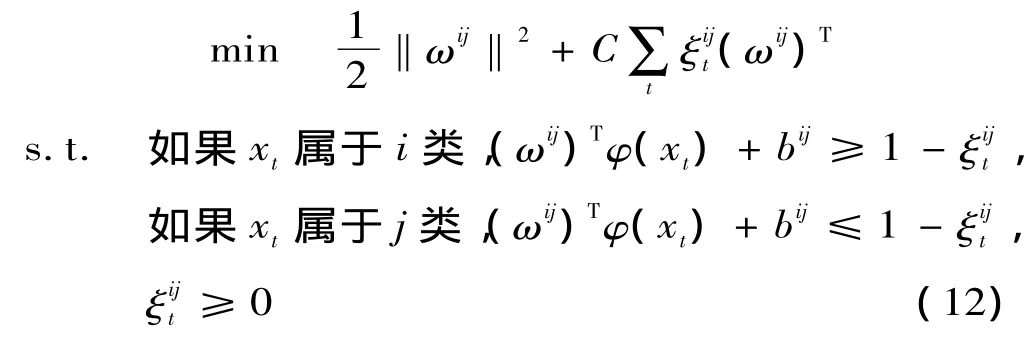
求解后根据((ωij)Tφ(x)+bij)的符号判断出x属于i和j中的哪一类，就记i类或j类一票，最后，把x划分到k类问题中得票最多的那一类。

3 滚动轴承故障诊断步骤

(1)小波去噪。在所选取的滚动轴承的振动信号数据中，为了防止噪声的干扰，导致滚动轴承故障诊断准确率的降低，在进行能量特征提取之前，首先进行降噪处理。通过对软阈值和强制降噪这两类方法的比较，最终本文采用fixed form软阈值降噪法，对包含噪声的信号通过sym8小波进行5层分解。

(2)利用db12对降噪后的振动信号进行5层小波分解，分别提取第5层的低频信号以及第1到5层各层的高频信号。

(3)对所提取的低、高频信号进行小波分解系数重构并根据式 (9)提取信号能量，且依次记为 E1、E2、E3、E4、E5、E6。

(4)能量归一化处理［14］

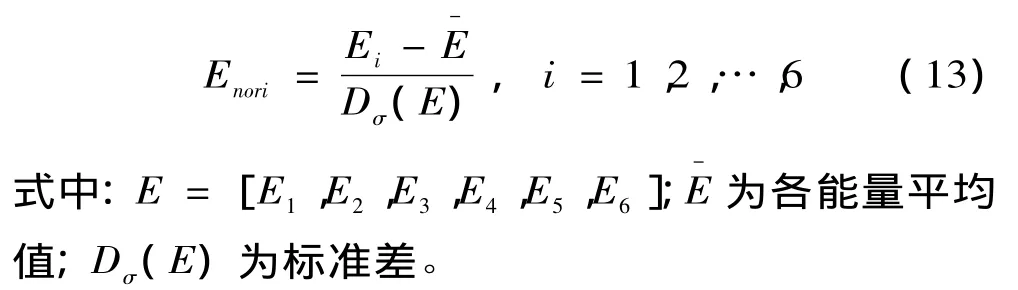
(5)得到的标准化的能量特征向量如下:

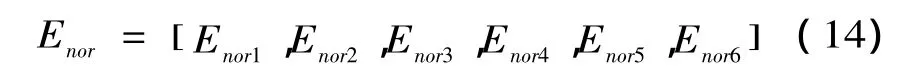
(6)将上述步骤得到的能量特征向量输入SVM中，进行滚动轴承故障严重程度的分类识别。

与轴承的内圈故障程度诊断步骤类似，滚动轴承的外圈和滚动体故障程度的研究也应按照上述步骤逐一实现，如图3所示，用数字1～5来表示滚动轴承的5种不同故障程度。

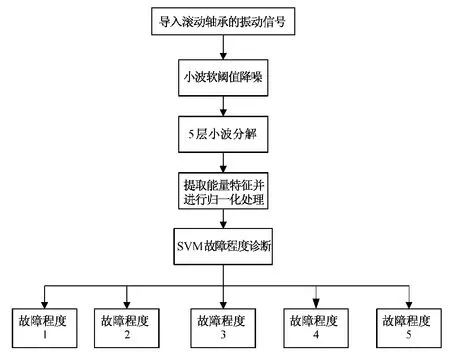
图3 滚动轴承故障程度诊断步骤

4 实测数据验证

实验数据取自美国Case Western Reserve University轴承数据中心［15］，驱动端所用的滚动轴承为SKF6205深沟球轴承，轴承故障类型包括内圈故障、外圈故障和滚动体故障三种，是由电火花加工出的单点损伤。由加速度传感器来采集振动信号，采样频率为12 kHz。为了研究滚动轴承故障的严重程度，选取了轴承的三种故障的振动数据，且滚动轴承的载荷为零，故障尺寸分别为0 mm(正常状态)、0.18 mm、0.36 mm、0.53 mm、0.71 mm，但由于实验数据限制，针对滚动轴承的外圈故障，故障尺寸只包括上述5种情形的前4种。实验结果分析如下。

针对滚动轴承内圈、外圈、滚动体这三种故障的不同严重程度，每种故障尺寸都计算得到了50个标准化的能量特征向量，随机选取其中30个数据样本作为训练集，剩下的20个样本则作为测试集。对于训练集，采用5折交叉验证和网格搜索的方法，得到最佳核函数参数γ和惩罚因子C后，也就得到了训练好的SVM模型，可以进行测试集的分类识别，分类结果如表1～3所示。

从表1和表3中可以看出，对于滚动轴承内圈故障的5种不同的严重程度，100个测试样本中包含了4个错分样本;对于滚动体故障，错分样本数则较多，达到了8个，其中，错分样本主要集中在故障尺寸0.53 mm这一类，具体表现为将该类故障错分到0.18 mm和0.36 mm这两类中，说明该方法对滚动体故障程度的分类效果并不十分理想。而表2显示，针对滚动轴承外圈故障严重程度的分类，其准确率达到了100%。综合上述三种情形，提出方法虽然有一定局限性，但总体来说，还是可以比较准确地识别出滚动轴承不同故障的严重程度。

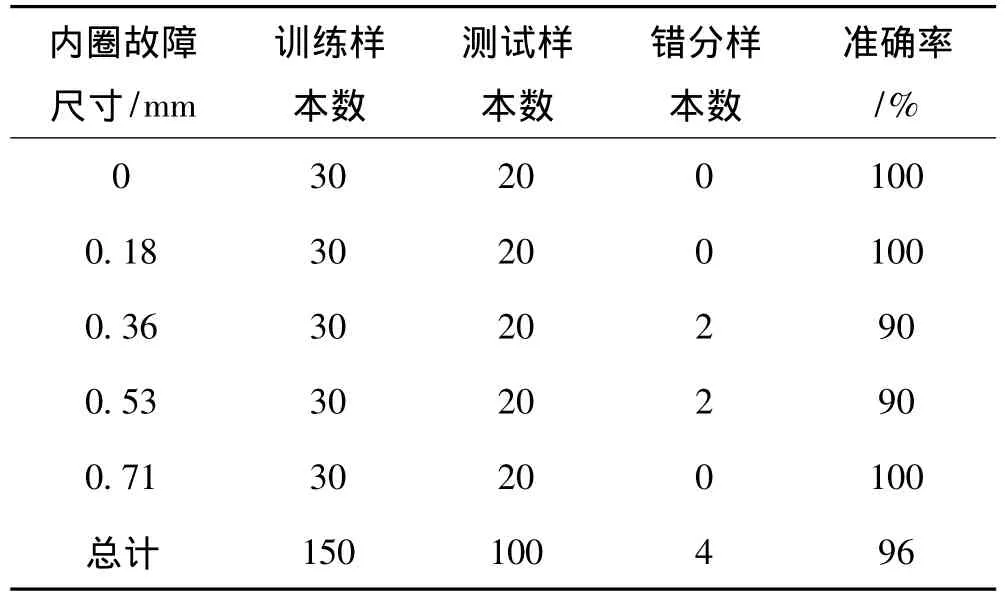
表1 滚动轴承内圈故障严重程度诊断结果

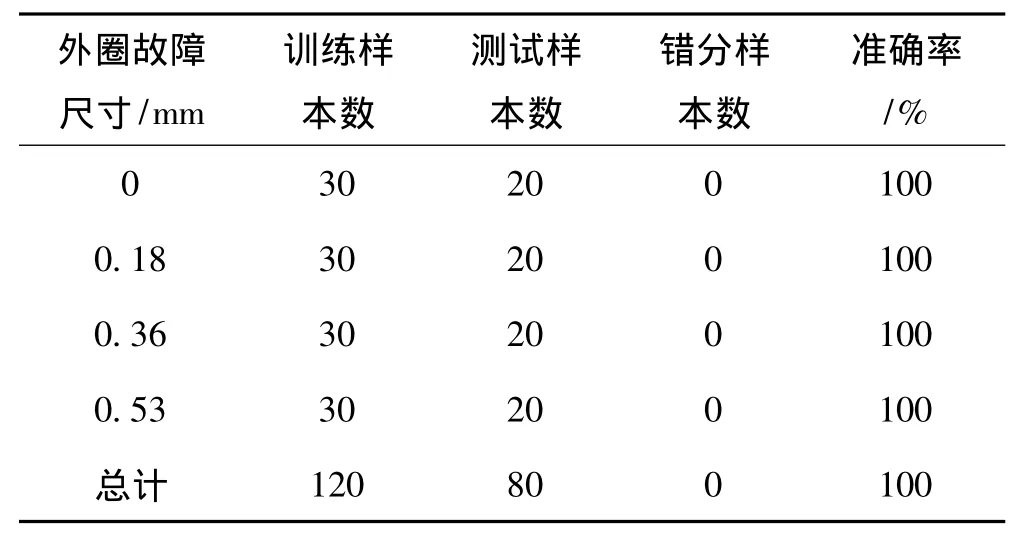
表2 滚动轴承外圈故障严重程度诊断结果

表3 滚动轴承滚动体故障严重程度诊断结果

5 结论

在本文中，利用小波分解和SVM的自身优势，将二者合理地结合到一起来实现滚动轴承不同故障程度的识别诊断，而帕塞瓦尔能量提供了滚动轴承振动信号经过小波分解后各个频带的能量分布信息。最后经实测数据的计算检验，发现该方法不仅可以降低噪声的影响，而且可以通过合理的能量特征提取方式来达到比较高的识别率，表明了所提方法的有效性。因此，该方法对于滚动轴承不同故障严重程度的诊断是可行的。但同时，该方法也有其自身的局限性，每次只能针对滚动轴承的一种故障进行研究，不能在三种故障同时存在的情况下得到较高的分类准确率。

［1］胡耀斌，谢静，胡良斌．基于神经网络与小波变换的滚动轴承故障诊断 ［J］．机械设计与研究，2013，29(6):33－35．

［2］张昭，杜冬梅．基于LMD能量信号和1.5维谱的轴承故障分析 ［J］．电力科学与工程，2015，31(5):6－10．

［3］徐振辉，马立元．滚动轴承的故障特征提取 ［J］．兵工自动化，2004，23(1):46－48．

［4］赵志宏，杨绍普．基于相对小波能量的滚动轴承故障诊断［J］．电子测量与仪器学报，2011，25(1):44－49．

［5］李舜酩，郭海东，李殿荣．振动信号处理方法综述［J］．仪器仪表学报，2013，34(8):1907－1915．

［6］肖迎群，何怡刚．基于小波分形分析和脊波网络的模拟电路故障诊断方法 ［J］．电工技术学报，2011，26(11):105－114．

［7］刘美容，张立玮．基于小波分解和模糊聚类的模拟电路软故障诊断 ［J］．微电子学与计算机，2014，(12):140－143．

［8］Ren Z H，Zhou S H，Chunhui E，et al．Crack fault diagnosis of rotor systems using wavelet transforms［J］．Computers and Electrical Engineering，2015，(45):33－41．

［9］陈刚，廖明夫．基于小波分析的滚动轴承故障诊断研究［J］．科学技术与工程，2007，7(12):2810－2814．

［10］严峰，陈晓，王新民，等．改进的离散小波－优化极限学习机在倾转旋翼机故障诊断中的应用 ［J］．兵工学报，2014，35(11):1914－1921．

［11］ VAipnik V N．The Nature of statistical learning theory［M］．New York:Springer，1999．

［12］张倩，杨耀权．基于支持向量机核函数的研究［J］．电力科学与工程，2012，28(5):42－45．

［13］Patel V N，Tandon N，Pandey R K．Defect detection in deep groove ball bearing in presence of external vibration using envelope analysis and Duffing oscillator［J］．Measurement，2012，45(5):960 －970．

［14］徐涛，裴爱岭，刘勇．基于谐波小波包和SVM的滚动轴承故障诊断方法 ［J］．沈阳航空航天大学学报，2014，31(4):50－54．

［15］ The Case Western Reserve University Bearing data center Website．Bearing data center seeded fault test data［DB/OL］．http://csegroups．case．edu/bearingdatacenter/pages/download-data-file，2012-11-15．

Research on Rolling Bearing Fault Degree Based on Wavelet Decomposition and Support Vector Machine

You Xiaofei，He Qing

(School of Energy Power and Mechanical Engineering，North China Electric Power University，Beijing 102206，China)

A rolling bearing fault diagnosis method is proposed in this paper that based on wavelet decomposition and SVM to extract fault feature．First，the original vibration signals were processed by wavelet de-noising in order to reduce error，and then wavelet was decomposed and the decomposed wavelet was used to calculate the energy characteristics using the wavelet reconstruction coefficient．After normalization，they were input into SVM as feature vector to realize fault diagnosis．The experiment results show that the proposed method is effective in fault feature extraction，and has high accuracy of fault diagnosis．The method can accurately distinguish the severity of rolling bearing faults．

rolling bearing;fault diagnosis;wavelet decomposition;support vector machine

TH 133.33

A

10.3969/j.issn.1672-0792.2015.11.013

2015－09－17。

中央高校基本科研业务费专项资金资助 (2014XS25)。

尤晓菲 (1992-)，女，硕士研究生，研究方向为滚动轴承的状态监测与故障诊断，E-mail:happy920308@163.com。

book=74,ebook=558