电池储能平抑风电功率波动的预测控制方法
罗 毅,李 达
(华北电力大学 控制与计算机工程学院,北京102206)
电池储能平抑风电功率波动的预测控制方法
罗毅,李达
(华北电力大学 控制与计算机工程学院,北京102206)
摘要:风电波动性和随机性严重影响电力系统安全稳定性。为了平抑风功率波动,提出了一种基于模型预测控制(MPC)原理的平抑风电功率波动的电池储能控制方法。该方法利用风电场超短期功率预测信息,以并网风电功率的波动范围、电池储能荷电状态(SOC)、储能出力大小等为约束,通过滚动优化实现对储能的优化控制。算例表明,该方法既能有效平抑风电功率波动,又能超前控制储能SOC值,维持储能的平滑能力,避免储能过充过放。
关键词:风功率波动;电池储能系统;荷电状态;模型预测控制
中图分类号:TM614
文献标识码:��码: A
DOI:10.3969/j.issn.1672-0792.2015.11.001
收稿日期:2015-09-25。
基金项目:北京市自然科学基金(4122071)。
作者简介:罗毅(1969-),男,教授,研究方向为工业过程建模、仿真、优化控制与决策, E-mail:591273306@qq.com。
Abstract:The fluctuation and randomness of wind power harmfully impacts on the security and stability of power system. In order to smooth the fluctuation of wind power, a new control strategy for battery energy storage system(BESS)based on the model predictive control (MPC) is proposed. Based on the super short-term power forecasting results, an optimal control of the energy storage system is realized through receding optimization with a number of constrains considered such as the fluctuation range of grid-connected wind power, the state-of-charge (SOC) of the energy storage system and energy storage output size. Simulation studies demonstrate that the new method can not only smooth the short-term fluctuation, but also control the SOC range ahead, thus maintaining the smoothing performance of BESS and avoiding overcharging and discharging.
Keywords:wind power fluctuation; battery energy storage system; state of charge; model predictive control

0引言
随着风力发电技术的快速发展,并网风电的规模和比例会不断加大,风电功率的间歇性和波动性将给电力系统的安全稳定运行带来严重挑战[1~3]。为了调高风电并网的能力,需要对并网风电功率的波动进行平抑[4,5]。随着储能技术和种类的发展,储能已经成为平抑风力波动的有效手段[6]。
目前,利用储能系统平抑风电功率波动的控制方法的研究已有一些成果。一阶低通滤波算法因其原理简单、运算速度快得到广泛应用[7~9],但其跟踪风电功率变化的能力不足。文献[10,11]提出了根据储能荷电状态(SOC)改变滤波时间常数的变时间常数低通滤波算法,避免了储能的过充电和过放电。文献[12]采用小波包分解理论将风电平抑功率进行分配,利用功率型和能量型储能同时平抑风电功率波动。文献[13]根据超级电容器荷电状态的反馈信息,采用模糊算法修正超级电容器出力的大小,以避免其过充电或过放电。但是这些控制方法不具备对未来风电功率变化的预判能力,在风电功率连续变化时容易导致储能SOC越限,导致储能使用寿命的减少并削弱储能下一时刻平抑风电功率波动的能力。
模型预测控制(MPC)具有对系统未来动态行为的预测能力以及显示处理约束的能力,是近年来被广泛运用在工业控制中的一种先进控制策略。超短期风功率预测技术也应用到了风功率波动平抑应用中。文献[14]利用未来15 min风功率预测信息,利用遗传算法进行滚动优化,实现了对风电功率波动的实时平抑。
基于以上分析,本文提出一种电池储能平抑风电功率波动的预测控制方法。该方法基于15 min超短期风功率预测技术,以储能荷电状态偏离理想值和储能出力最小为优化目标,考虑并网风电功率的波动范围等约束,利用在线滚动优化策略对储能功率进行实时控制,优化结果在有效平抑风功率波动的同时可以提前控制储能SOC值,使其维持在理想范围内,防止储能过充过放,提高储能平抑能力的可持续性。
1风储联合发电系统
图1为风储联合发电系统的结构示意图。如图所示:Pw为实时风电场发电功率;Pb为储能实时输出功率;Pb-ref为储能控制器的输出的指令值,放电时取正值,充电时取负值;Pg为该联合系统实时并网功率。
由系统的能量平衡可知:

图1 风电场和储能联合运行系统结构
(1)
控制器通过一定的控制策略,根据采集到的系统各种信息来实时改变储能的输出功率,从而协调风电场的出力,改变风电场的出力特性,使风电场能满足并网的标准。
2电池储能系统的技术特性
储能的使用寿命与储能充放电时的荷电状态密切相关。如文献[15]报道的某款电池,当放电深度为20 %时,循环寿命为4 200次,而当放电深度提高至80 %时,其循环寿命则缩短为2 500次。铅酸电池的放电深度达到80 %左右时循环寿命仅为几百次。所以在储能平抑风功率波动时,要根据储能的荷电状态进行控制,防止储能过冲过放,提高储能的使用寿命。
SOC为储能剩余容量占其总容量的百分比。其与充放电之间的关系可用以下公式表示:
(2)
式中:S(k)为时段k储能系统的荷电状态;EB为储能系统总容量;Δt为单位时段的时间间隔。
为了提高储能的使用寿命,防止储能因SOC越限而发生功率畸变,储能设备的SOC在使用期间需保持在一个合理的范围内,即
(3)
式中:S(k)为时段k储能系统的荷电状态;Smin和Smax分别为储能系统荷电状态的最小允许值和最大允许值。
综上所述,储能荷电状态是对储能进行控制的重要依据。能量的过充过放不仅会影响储能的使用寿命,还会削弱下一时刻对风功率波动的平抑能力。 所以储能在平抑风力波动时,需使储能的荷电状态保持在理想范围内。
3基于MPC的储能控制方法
MPC采用滚动式的有限时域优化策略。在每一采样时刻,根据该时刻的优化性能指标,求解一个从该时刻起有限时域的最优控制问题,解得的最优控制序列只实施第一个控制作用。
风电功率预测精度随预测周期的变大而降低。目前最快的超短期风功率预测区间为15 min,步长为1 min[14]。基于此,MPC预测时域取为10 min,控制时域取为1 min,储能的控制周期取为20 s。
3.1 MPC系统模型
风储联合发电系统的状态空间模型如下:
(4)
(5)
式中:u(k)表示并网功率Pg(k);r(k)为风电功率Pw(k);x1(k)为储能输出功率Pb(k);x2(k)为储能剩余容量Eb(k);y(k)为过程输出向量。
本文中,用k表示MPC的控制时刻,其间隔为20 s。
系统目标函数如下:
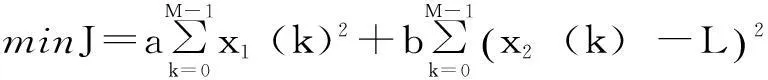
(6)
式中:L为储能容量处于理想状态时的SOC值;a和b为惩罚系数。式(6)中的2个惩罚项分别为对储能出力和储能容量偏离理想值的优化。
模型约束条件如下:
(1)并网功率约束
(7)
式中:Prated为风电场额定功率。
(2)储能功率约束
(8)
式中:Pch和Pdch分别为储能最大充放电功率。
(3)储能容量约束
EBSmin≤y2(k)≤EBSmaxk=0,1,…,M-1
(9)
(4)风功率波动平抑约束
并网风功率波动约束要参考风电场爬坡率的国家标准,如表1所示。

表1 风电场最大功率变化率国网推荐值
本文采用电力系统中普遍采用的爬坡率计算方法,得到风功率波动平抑约束为:
(10)
式中:γ表示爬坡率占风电场额定功率的比重系数。
3.2 MPC优化问题求解
在控制时刻k,MPC控制器以系统当前时刻的状态x(k)作为起始状态,采用在线滚动优化的方法求解预测时域内满足系统各种约束的开环最优控制问题。
记Y=[Y1;Y2;U],其中
(11)
(12)
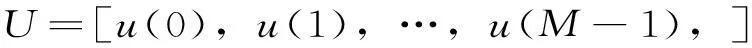
(13)
则功率波动平抑问题可以转化为以下形式:
(14)
式中:Φ为二次项系数矩阵;φ为一次项系数矩阵。
约束条件表示为:

(15)
式中: f(Y)为非线性函数; ω为一维列向量。式(15)表示的是优化问题的非线性不等式约束,这是典型的二次规划(QP)问题。
3.3 约束的松弛和调整
当储能SOC越限或者风功率剧烈波动时,储能无法对风力波动进行有效平抑,使得风电场输出功率不满足系统的约束,程序无可行解。此时应该对系统的约束进行松弛,使问题收敛得到可行解,因此原优化目标要改为:
(16)
式中:ρ为惩罚系数(非负);ε为松弛向量(非负),仅当约束不可行时不为0。
约束条件变为:
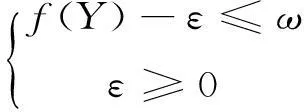
(17)
式(17)仍是QP问题。通过约束软化,使得该算法得到当前时刻可行的最优解。
4算例分析
4.1 电池储能容量配置
基于某装机容量Prated为60 MW的风电场风功率历史数据,分别选取春、夏、秋、冬四季中4个典型日的风电出力数据,采用本文方法,计算在满足风功率并网指标的情况下BESS的最大出力与容量,结果见表2。

表2 典型日下BESS最大出力与容量
根据以上数据,使用Matlab对本文方法进行仿真分析,比较不同控制策略的控制效果。储能最大功率设置为10 MW,容量配置为5 MW·h,储能理想SOC为50 %,SOC允许变化范围为[0.2,0.8]。MPC控制器调节储能输出功率的周期为20 s,惩罚系数a=1,b=2,。根据表1,式(10)中γ取为1/10。
4.2 MPC的风电功率波动平滑效果
选取该风电场典型情况下连续1 h风电功率数据,图2为原始风电功率和平滑后的并网功率波动情况,图3 为相应的储能SOC变化变化曲线。
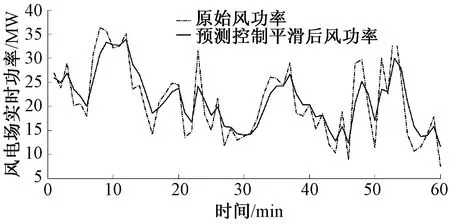
图2 平抑波动控制仿真结果
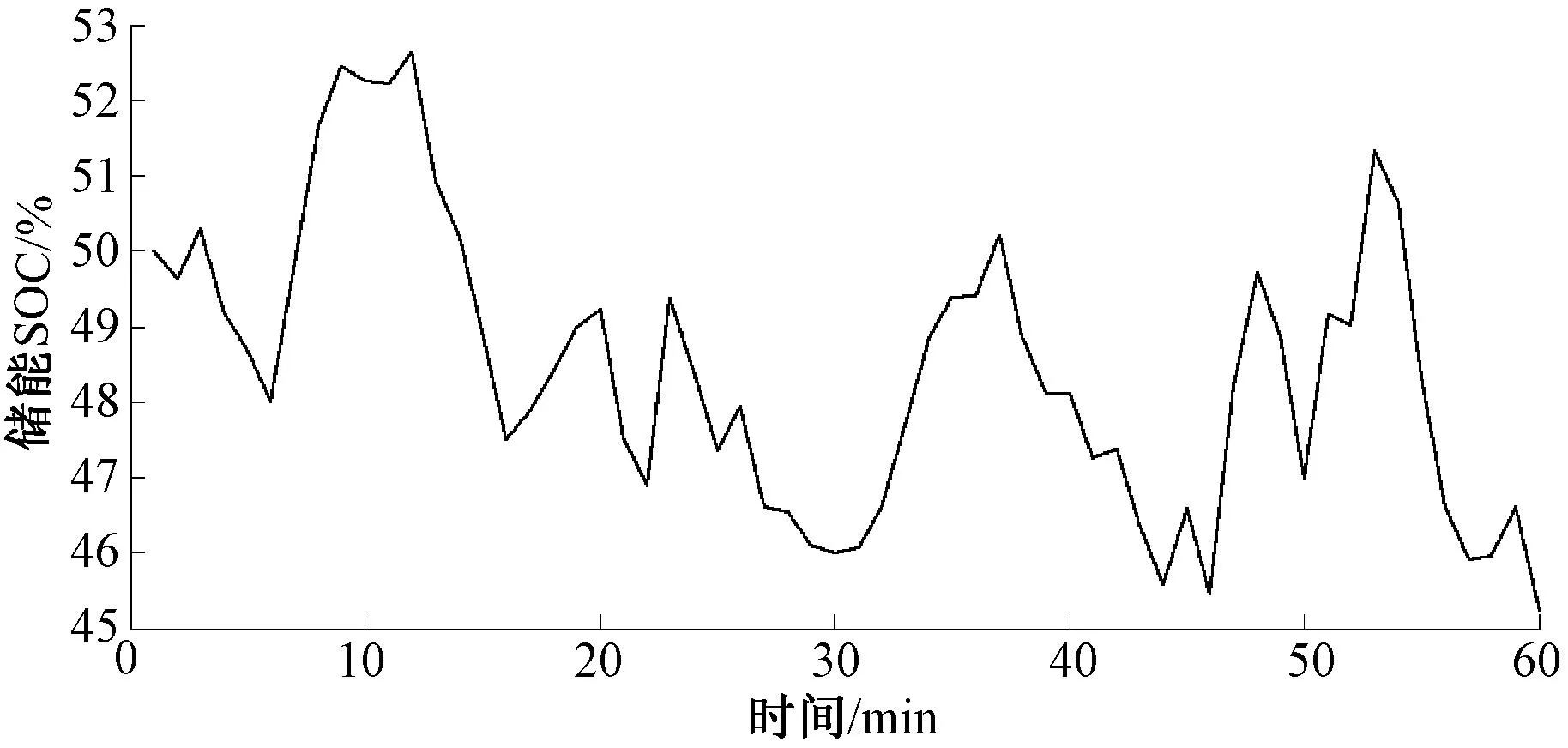
图3 储能SOC变化曲线
由图2和图3可知,本文提出的模型预测控制方法能够有效平抑风功率波动,并网风功率的波动能满足电网要求,电池储能的荷电状态也维持在合理范围内。
4.3 SOC控制效果对比
储能容量是一个定值,当风电功率在一定时间内出现大幅度的波动时,储能容易达到SOC的上下限额,使得储能平抑风力波动的能力不具有可持续性。所以,在典型的风功率剧烈波动的情况下,能否将储能SOC值控制理想值附近是评价风储系统控制策略的重要标准。本文分别采用可变滤波时间常数的低通滤波算法(方法1)和本文提出的MPC方法(方法2),选取一种典型的风功率剧烈波动的场景来比较不同方法的控制效果。
选取某典型风功率剧烈波动场景下2 h内风电功率数据,其初始时刻储能SOC为80 %,不久后风电功率骤升,如图4所示。
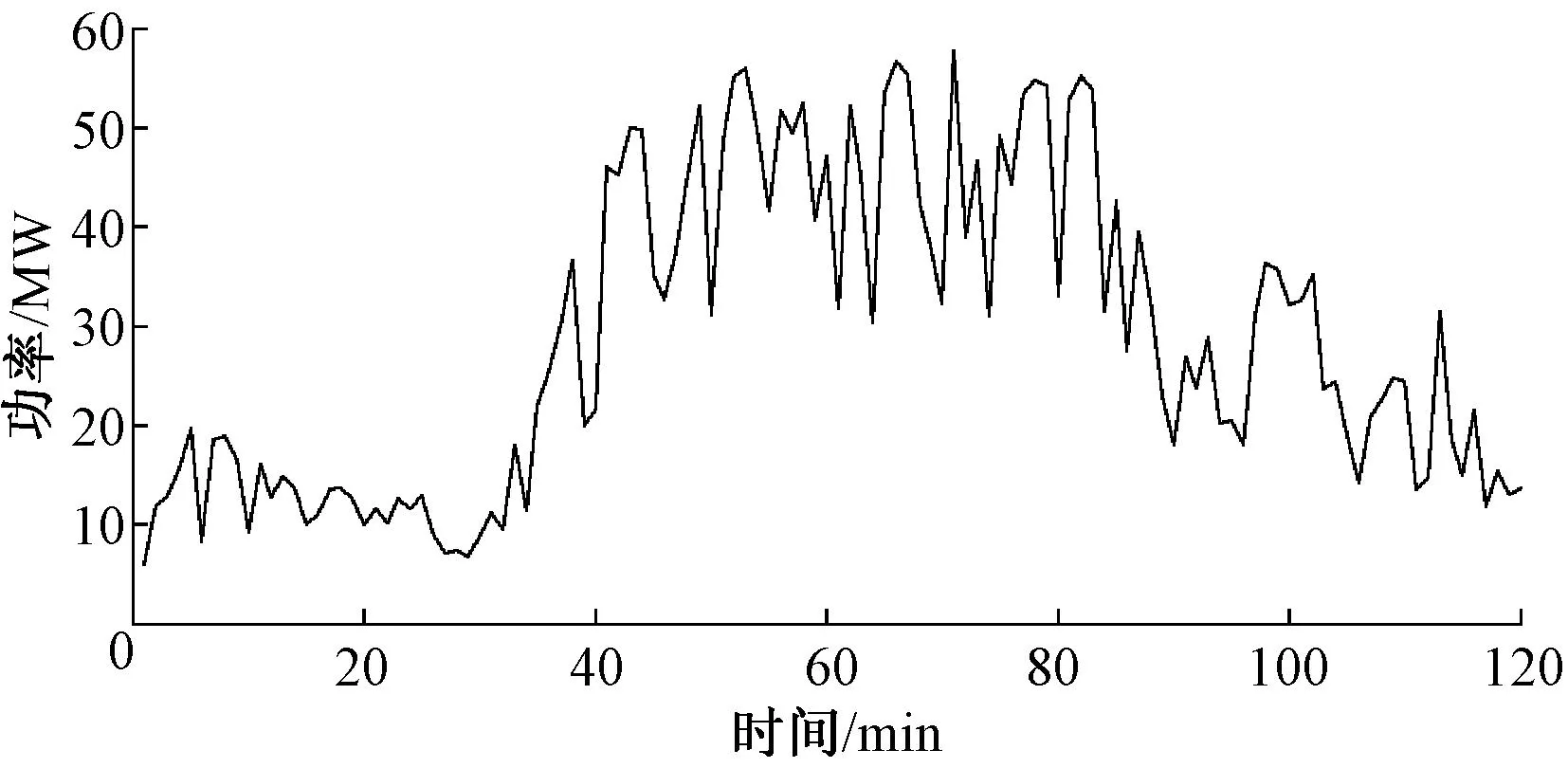
图4 极限场景下的风电功率曲线
图5反映了采用这两种方法对风功率进行平抑后储能SOC的变化情况。由图5可知,方法1虽然采取了可变滤波时间常数的控制方法,但当风功率连续剧烈波动时储能SOC仍会达到上下限值,从而削弱甚至失去平抑风电功率波动的能力;方法2利用MPC根据风功率预测信息通过提前放电使储能在风功率骤升之时拥有足够的充电容量,并维持储能SOC在的理想状态值附近。这是由于MPC利用风功率预测信息对储能功率进行调整,使储能SOC得到优化调整,这体现在式(6)中第二个惩罚项的作用。
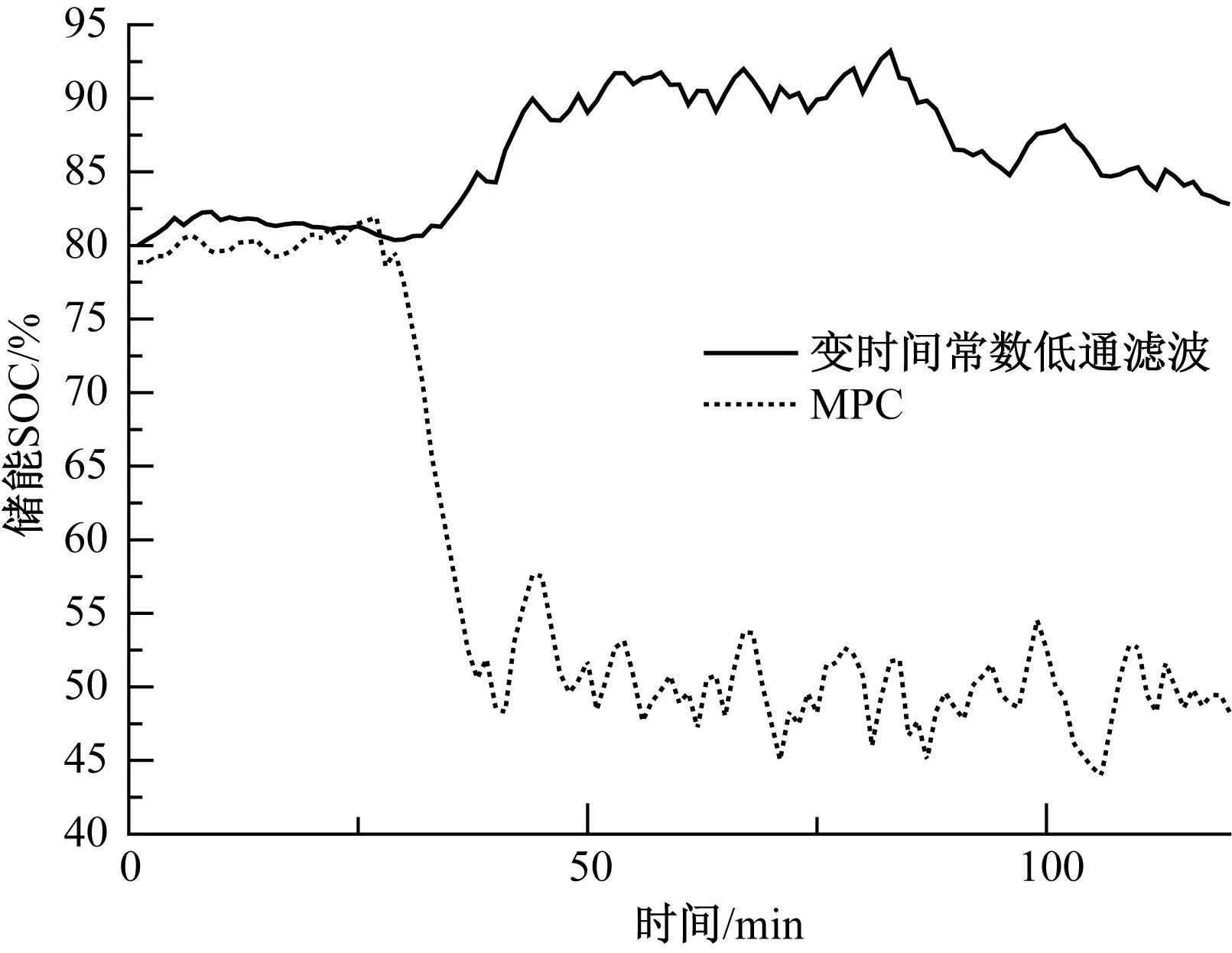
图5 风功率剧烈波动时储能SOC变化曲线
图6展示了在这种风功率剧烈波动的情况下采用两种方法得到的功率波动累计概率分布情况。由图可知,方法2利用了风功率预测信息,在风功率上升前能提前对储能进行适量的放电,为储能吸收功率提供了裕量,保证了储能的平抑能力,与方法1相比其平抑效果更符合风电并网的标准。
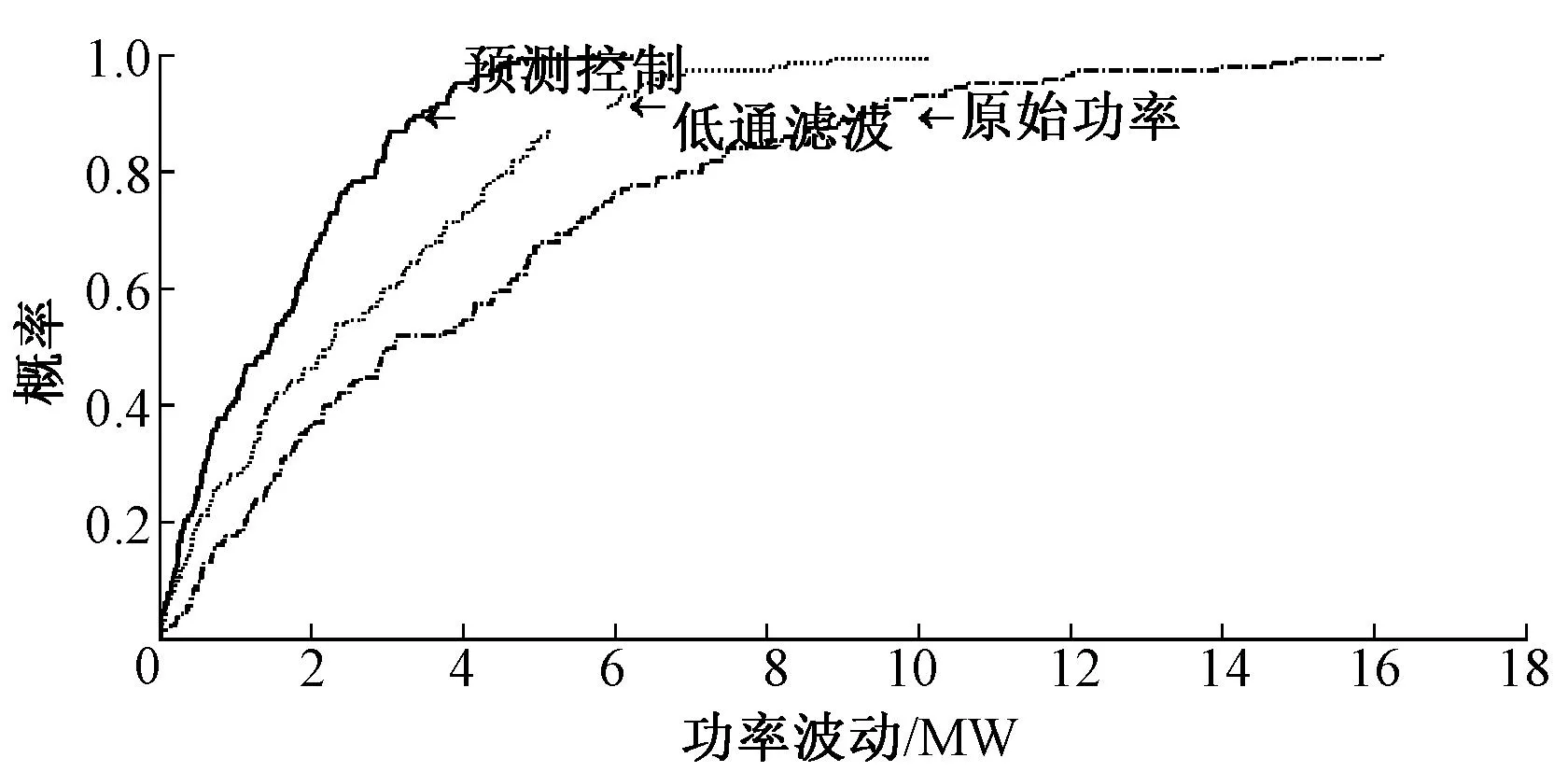
图6 场景1中1 min功率波动累计概率分布图
5结论
本文提出的基于模型预测控制原理的储能控制方法,利用了超短期风功率预测信息,具备对未来风电功率动态变化的预见性;通过在线滚动优化实时调节储能出力,在有效平滑风电功率波动的同时,能够将储能荷电状态控制在理想范围内,延长了储能使用寿命,提高了风储联合系统的经济性。
储能容量的大小与储能的平抑能力和风储联合系统的经济性有着直接关系,如何兼顾储能的平抑能力和系统经济性来确定储能容量是下一步的研究重点。
参考文献:
[1]李辉,栗树材,包伟华,等.并网风电场电压稳定的无功补偿策略[J].电力科学与工程,2013,29(9):13-17.
[2]王建,李兴源,邱晓燕.含有分布式发电装置的电力系统研究综述[J].电力系统自动化,2005,29(24):90-97.
[3]Liu X G,Xu Z,Wong K P.Recent advancement on technical requirements for grid integration of wind power
[J].Journal of Modern Power System and Clean Energy,2013,1(3):216-222.
[4]张丽英,叶廷路,辛耀中,等.大规模风电接入电网的相关问题及措施[J].中国电机工程学报,2010,30(25):1-9.
[5]于芃,周玮,孙辉,等.用于风电功率平抑的混合储能系统及其控制系统设计[J].中国电机工程学报,2011,31(17):127-133.
[6]童欣,郝剑波,张坤.锂电池储能在风力发电系统中的应用[J].电力科学与工程,2013,29(2):5-10.
[7]张国驹,唐西胜,齐智平.平抑间歇性电源功率波动的混合储能系统设计[J].电力系统自动化,2011,35(20):24-28.
[8]李国杰,唐志伟,吉林,等.钒液流储能电池建模及其平抑风电波动研究[J].电力系统保护和控制,2010,38(22):115-119.
[9]李霄,胡长生,刘昌金,等.基于超级电容器储能的风电场功率调节系统建模与控制[J].电力系统自动化,2009,33(9):86-90.
[10]张野,郭力,贾宏杰,等.基于电池荷电状态和可变滤波时间常数的储能控制方法[J].电力系统自动化,2012,36(6):34-38.
[11]刘霞,江全元.风光储混合系统的协调优化控制[J].电力系统自动化,2012,36(14):95-100.
[12]韩晓娟,陈跃燕,张浩,等.基于小波包分解的混合储能技术在平抑风电场功率波动中的应用[J].中国电机工程学报,2013,33(19):8-13.
[13]张坤,吴建东,毛承雄,等.基于模糊算法的风电储能系统的优化控制[J].电工技术学报,2012,27(10):235-241.
[14]王颖,张凯锋,付嘉渝,等.抑制风电爬坡率的风储联合优化控制方法[J].电力系统自动化,2013,37(13):17-23.
[15]Wan Y H.Summary report of wind farm data[R].Golden:National Renewable Energy Laboratory,2008.
A Model Predictive Control Method of Battery Energy Storage for Smoothing Wind Power Fluctuation
Luo Yi, Li Da(School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China)

