Full-f eld mapping of internal strain distribution in red sandstone specimen under compression using digital volumetric specklephotography and X-ray computed tomography

Lingto Mo,Jinping Zuo,Zexun Yun,Fu-Pen Ching

aState Key Laboratory of Coal Resources and Safe Mining,China University of Mining&Technology(Beijing),Beijing 100083,China

bLaboratory for Experimental Mechanics Research,Stony Brook University,Stony Brook,NY 11794-2300,USA

cDepartment of Mechanical Engineering,Stony Brook University,Stony Brook,NY 11794-2300,USA

Full-f eld mapping of internal strain distribution in red sandstone specimen under compression using digital volumetric speckle
photography and X-ray computed tomography

Lingtao Maoa,b,c,*,Jianping Zuoa,Zexun Yuana,Fu-Pen Chiangb,c

aState Key Laboratory of Coal Resources and Safe Mining,China University of Mining&Technology(Beijing),Beijing 100083,China

bLaboratory for Experimental Mechanics Research,Stony Brook University,Stony Brook,NY 11794-2300,USA

cDepartment of Mechanical Engineering,Stony Brook University,Stony Brook,NY 11794-2300,USA

A R T I C L E I N F O

Article history:

Received 20 November 2014

Received in revised form

26 January 2015

Accepted 28 January 2015

Available online 4 March 2015

Red sandstone

Strain localization

Uniaxial compression

Digital volumetric speckle photography

(DVSP)

X-ray micro-tomography

It is always desirable to know the interior deformation pattern when a rock is subjected to mechanical load.Few experimental techniques exist that can represent full-f eld three-dimensional(3D)strain distribution inside a rock specimen.And yet it is crucial that this information is available for fully understanding the failure mechanism of rocks or other geomaterials.In this study,by using the newly developed digital volumetric speckle photography(DVSP)technique in conjunction with X-ray computed tomography(CT)and taking advantage of natural 3D speckles formed inside the rock due to material impurities and voids,we can probe the interior of a rock to map its deformation pattern under load and shed light on its failure mechanism.We apply this technique to the analysis of a red sandstone specimen under increasing uniaxial compressive load applied incrementally.The full-f eld 3D displacement f elds are obtained in the specimen as a function of the load,from which both the volumetric and the deviatoric strain f elds are calculated.Strain localization zones which lead to the eventual failure of the rock are identi f ed.The results indicate that both shear and tension are contributing factors to the failure mechanism.

©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

The macroscopic deformation and failure of rock is a gradual process of damage accumulation,crack initiation,propagation, interaction and then the eventual failure(Amitrano,2006).Failure f rst manifests itself with the appearance of strain localization and then the creation of a damage zone.The localization of damage and strain will result in the stress redistribution and thus weaken the mechanical performance of the rock.In order to understand the mechanisms and evolution of damage or strain localization in rocks,full-f eld deformation measurement methods,such as stereophotogrammetry(Desrues and Viggiani,2004)and digital image correlation(DIC)(Kozicki and Tejchman,2007;Hall et al.,2010a,b; Dautriat et al.,2011;Nguyen et al.,2011;Lin and Labuz,2013;Zhang et al.,2013)have been used,mostly with two-dimensional(2D) images obtained from plane strain experiments.But the 2D observations are limited in their capability to resolve the geometric complexities and heterogeneity in geomaterials.

X-ray computed tomography(CT),as a non-destructive threedimensional(3D)imaging technique,has been used to investigate the internal structures,deformation localization and failure of geomaterials.In applications of the X-ray CT,the loading test and the scanning were not conducted simultaneously(Desrues et al., 1996;Alshibli et al.,2000).Only the density of the specimen or the CT number distribution inside the specimen was used to reveal the localized zones(Bésuelle et al.,2000;Viggiani et al.,2004;Louis et al.,2006;Suzanne et al.,2008).The 2D DIC technique has been employed to analyze radiography(Louis et al.,2007)or the sectional CT images(Adam et al.,2008)for assessing the internal deformation patterns in the geomaterials.A signi f cant limitation of this approach is the fact that it only allows the quanti f cation of 2D displacement f eld and 2D strain distribution in the sectional plane while ignoring the out-of-plane displacement all together(Adam et al.,2013).This information is not suf f cient to fully evaluate the onset and evolution of localized deformation.Bay et al.(1999) developed a 3D strain mapping technique using 3D digital image volume correlation,called digital volume correlation(DVC),and have measured displacement and strain f elds in trabecular bonesunder compression.By combining in situ CT scanning and DVC, some studies have been carried out on a number of geomaterials, such as rocks(Lenoir et al.,2007;Charalampidou et al.,2011,2014) and granular materials(Hall et al.,2010a,b;Adam et al.,2013).In the DVC method,a cubic subset surrounding the interrogated point located in the reference volume image is selected and correlated with the corresponding location in the deformed volume image. The resulting displacement vector is obtained.The theory is simple. But in the practical implementation due to the vastly increased volume of data associated with the undeformed and deformed images and the increased degree-of-freedom(DOF),the DVC is facing some challenges,such as the implementation complexity, the measurement accuracy and the computational ef f ciency(Pan et al.,2012).Digital volumetric speckle photography(DVSP)is another 3D strain analysis technique,which is the extension of 2D digital speckle photography(DSP)technique that offers some advantages over the DVC technique in the computational ef f ciency. Details of the evolution of the speckle technique leading to the development of DVSP can be found in Chiang and Mao(2015).

In this study,we apply the DVSP technique in conjunction with X-ray micro-tomography to obtain the 3D interior strain f elds in a red sandstone specimen under uniaxial compression,and then discuss the accuracy of DVSP technique.

2.Experimental procedure

2.1.Experimental setup and imaging procedure

In this study,the main components of the industrial X-ray CT system are a microfocus X-ray source from YXLON(FeinFocus 225 kV),a X-ray detector unit(1024 pixel×1024 pixel)from PerkinElmer(XRD 0822AP 14),and a motorized rotation stage from Newport,USA.The X-ray has a focus with size of 3μm×6μm,a voltage range of 50-225 kV,and the tube current ranging from 0 to 1440μA.A simple uniaxial compression setup is designed and built that would allow the operation of micro-tomography of a specimen under load in situ.The setup cell is made of PMMA,which is transparent to X-rays.The CT system and loading setup are shown in Fig.1.

A cylindrical specimen of red sandstone ofφ25 mm×50 mm in size and a porosity of 23.3%is placed in the cell.The compaction of the specimen is achieved by applying a compressive load in the axial(z)direction.The X-ray source to the specimen and source-todetector distances are 139 mm and 696 mm,respectively,resulting in a 5.0 times magni f cation.The whole compression process is divided into 8 steps.In each step,the loading is kept constant while the specimen is scanned.During the scanning,720 projections are captured and distributed at equal angles over 360°.It takes 25 min to scan the specimen in each loading step.After scanning,the reconstruction is carried out with the Feldkamp cone-beam reconstruction algorithm.The reconstructed volume images have 566 voxel×566 voxel×954 voxel(where a“voxel”is the 3D equivalentof a pixel)and cover the specimen with height of 43 mm. The physical size of a voxel is 45μm3.Based on the projection image of the specimen in each loading step,the global displacement alongz-axis is measured,from which the axial strain is obtained.The stress-strain curve from the loading history is shown in Fig.2. Because the metal compression disks in f uence the top and bottom slice images,only the middle of the volume image with size of 566 voxel×566 voxel×801 voxel is analyzed.In Fig.3,the reconstructed volume image of step 8,three orthogonal sections,and sectional images alongx=12.5 mm andy=12.5 mm of steps 7 and 8 are shown,respectively.

Fig.4 shows the gray value distribution curves throughout the volumetric images at different loading steps.It is noted among these curves that the distributions for steps 6 and 7 are slightly narrower than those of other steps.Table 1 lists the mean gray values and the standard deviations.It can be seen that the mean gray value has a slightly higher increment from step 1 to step 4, indicating globally a lower porosity and higher density;and then declines after step 4,indicating a higher porosity and lower density. This implies that the initial microcracks are closed under compressive loading before step 4,and microcrack development makes the specimen dilatant after step 4.However,gray value distribution curves and CT gray level images alone are not very effective in differentiating the strain localization area nor the microcrack onset and development.Thus,to shed more light on the deformation characteristics of the specimen,the newly developed full-f eld strain measurement technique,DVSP,is employed as follows.

Fig.1.Industrial CT and loading setup.

2.2.Elements of the DVSP technique

From the sectional images shown in Fig.3,it can be seen that there are several components and pores in the red sandstone,and different components have different gray values.This natural structure can be regarded as a pattern of volumetric speckles pattern and carries the information of deformation.This naturally presented structural pattern is used in the analysis adopting the DVSP technique.The volumetric image of step 1 is de f ned as the reference volumetric image,and the volumetric image of step 2 is de f ned as the deformed one.They are then divided into subsets with a cubic array of 64 voxel×64 voxel×64 voxel;there is a 32-voxel overlap between neighboring subsets,and then compared.The schematic of the processing algorithm of DVSP is demonstrated in Fig.5.

Fig.2.Stress-strain curve.

Leth1(x,y,z)andh2(x,y,z)be the gray intensity functions of a pair of generic volumetric speckle subsets,before and after deformation,respectively,we have

Fig.3.Reconstructed image and sectional images.(a)Reconstructed image of step 8; (b)Three orthogonal sections;(c)Section alongx=12.5 mm at step 7;(d)Section alongy=12.5 mm at step 7;(e)Section alongx=12.5 mm at step 8;(f)Section alongy=12.5 mm at step 8.

Fig.4.Gray value distribution curves of the volumetric images.

whereu,vandware the displacement components experienced by the speckles along thex,y,andzdirections,respectively.A f rst-step 3D fast Fourier transform(FFT)applied to bothh1andh2yields

whereH1(fx,fy,fz)andH2(fx,fy,fz)are the Fourier transforms ofh1(x,y,z)andh2(x,y,z),respectively;ℑ stands for Fourier transform; |H1(fx,fy,fz)|and|H2(fx,fy,fz)|are the spectral amplitudes ofH1(fx,fy,fz)andH2(fx,fy,fz),respectively;Φ1(fx,fy,fz)andΦ2(fx,fy,fz)are the phases ofH1(fx,fy,fz)andH2(fx,fy,fz),respectively.

Then,a numerical interference between the two 3D speckle patterns is performed at the spectral domain,i.e.

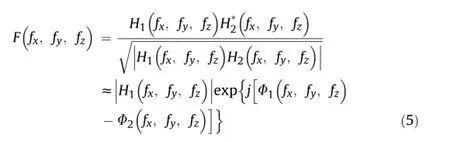
It is seen that

Finally,the following function can be obtained by performing another 3D FFT:

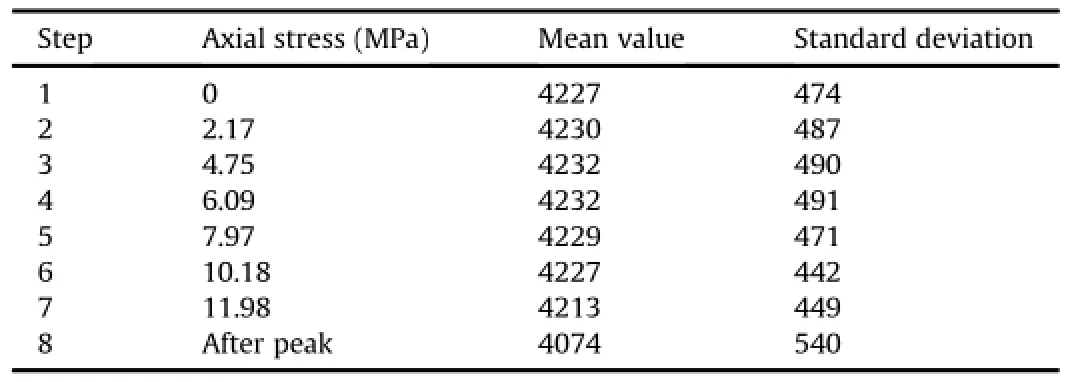
Table 1Statistics of gray values.

Fig.5.Schematics demonstrating the processing algorithm of DVSP.

Eq.(7)is an expanded impulse function located at(u,v,w). This process is carried out for every corresponding pair of the subsets.By detecting the crest of all these impulse functions,an array of displacement vectors at each and every subset is obtained.

Because of the discrete nature of digital volume images,the displacement vectors evaluated from Eq.(7)are integer multiples of one voxel.We select a cubic subset with 3 voxel×3 voxel×3 voxel surrounding an integer voxel of the crest and a cubic spline interpolation is employed to obtain the sub-voxel accuracy.From 3D displacement f elds,the internal strain tensor3can then be calculated using an appropriate strain-displacement relation.

2.3.Strain computation

The internal strain tensor3can be derived from the displacement f elds.If the displacement measurements involve errors,errors may be ampli f ed during the strain computation.In this study, we use the point-wise least-squares(PLS)approach(Pan et al., 2009,2012)to calculate strain tensors.In the PLS approach,the errors in local displacement f elds can be signi f cantly reduced during the process of local f tting.

To compute the local strains of each point considered,a regular cubic box with size of(2N+1)×(2N+1)×(2N+1) discrete points surrounding the considered point is selected. If the strain calculation window is small enough,the displacements in each direction can be reasonably assumed to be linearly distributed,and therefore can be mathematically expressed as

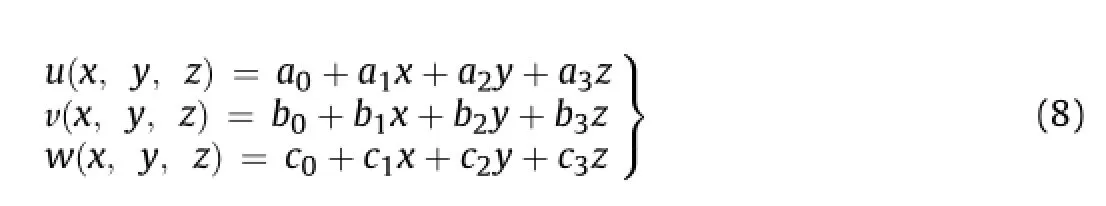
wherex,y,z=[-N,N]are the local coordinates within the strain calculation box;u(x,y,z),v(x,y,z)andw(x,y,z)are the displacements directly obtained by the DVSP method;andai,biandci(i=0, 1,2,3)are the unknown polynomial coef f cients to be determined. With the least-squares or multiple regression analysis,the unknown coef f cients can be estimated.Then,the six Cauchy strain components3x,3y,3z,3xy,3xz,3yzat the interrogated point can thus be calculated as

In the afore described processing scheme,the volume image of step 1 is kept as the reference image and the subsequent deformed images are“compared”to the reference image sequentially from which the displacement f elds and strain f elds in each step are calculated.The size of the volume image used in the calculation has 566 voxel×566 voxel×801 voxel.The subset size has 64 voxel×64 voxel×64 voxel,and there is a 32-voxel overlap between neighboring subsets.

3.Results

3.1.Displacementfelds

Theu,vandwdisplacement f elds of the specimen along thex-,y-andz-axes at step 7 are illustrated in Fig.6,respectively.

At the step 7,theudisplacement ranges from-110μm to 61μm, thevdisplacement from-95μm to 84μm,and thewdisplacement from 185μm to 376μm.As expected,the largest displacements occur in the top region along thez-axis.Due to the heterogeneity of the red sandstone specimen,the deformation is not uniform and with different features in different sections.We select two orthogonal sections alongx=12.5 mm andy=12.5 mm at different steps,representing the motion of the material in these sections along thex-,y-andz-axes,respectively,as shown in Figs.7-9.The analyzed areas correspond to the rectangular areas marked with dash lines in Fig.3e and f.In Figs.7 and 8,it is noted that the regions with the negative and positive displacements manifest themselves more clearly as the load increases.The interface between the two regions has zero displacement and is marked by a dash line in Figs.7c and 8c.At step 8,the specimen is broken, and the main cracks shown in Fig.3e and f are mainly predicated by the zero displacement interface,i.e.along the marked dash lines.

Fig.6.Displacement f elds of the specimen at step 7.(a)uf elds,(b)vf elds,(c)wf elds.

3.2.Strainfelds

In general,the strain distribution provides more information on the characteristics of deformation localization and damage evolution in the rocks.Derived from the above displacement f elds,six Cauchy strain components are computed by using PLS approach, and then the principal strains are obtained.The deviatoric strain3s and the volumetric strain3vare written as

where31,32and33are the major,intermediate and minor principal strains,respectively.

The evolution of deviatoric strain f elds and the volumetric strains is illustrated in Figs.10 and 11,respectively.At the axial stress level of 6.09 MPa,it can be seen from Fig.10a that some regions in lighter color indicate the presence of higher deviatoric strain value as a result of the material heterogeneity,leading to the formation of microcracks.At this stress level,the mean volumetric strain is-770×10-6,indicating the volume reduction of the specimen under compression.At the axial stress level of 7.97 MPa,a strain localization region appears as indicated by the dash line loop marked in upper of Fig.10b.As the load increases,the strain localization region starts to extend upward and new regions are generated as shown in upper of Fig.10c.The location of this region roughly corresponds to the macrocrack shown in Fig.3e.This implies that the crack is caused by shear stress.In the volumetric strain distribution maps depicted in upper of Fig.11b and c,the volumetric strain in this region also rises.When the stress level increases from 7.97 MPa to 11.98 MPa,the volumetric strain growsrapidly as shown in Fig.11c,and the specimen dilates.The high strain region largely matches the macrocracks shown in Fig.3e and f.Judging from the patterns of crack shape and strain distribution,it is reasonable to state that the specimen destruction is combination of tension failure and shear failure.

Fig.7.Distribution ofudisplacement f elds of two orthogonal sections at different steps.(a)Step 4(axial stress=6.09 MPa),(b)Step 5(axial stress=7.97 MPa),(c)Step 7(axial stress=11.98 MPa).

Fig.8.Distribution ofvdisplacement f elds of two orthogonal sections at different steps.(a)Step 4(axial stress=6.09 MPa),(b)Step 5(axial stress=7.97 MPa),(c)Step 7(axial stress=11.98 MPa).

Fig.9.Distribution ofwdisplacement f elds of two orthogonal sections at different steps.(a)Step 4(axial stress=6.09 MPa),(b)Step 5(axial stress=7.97 MPa),(c)Step 7(axial stress=11.98 MPa).

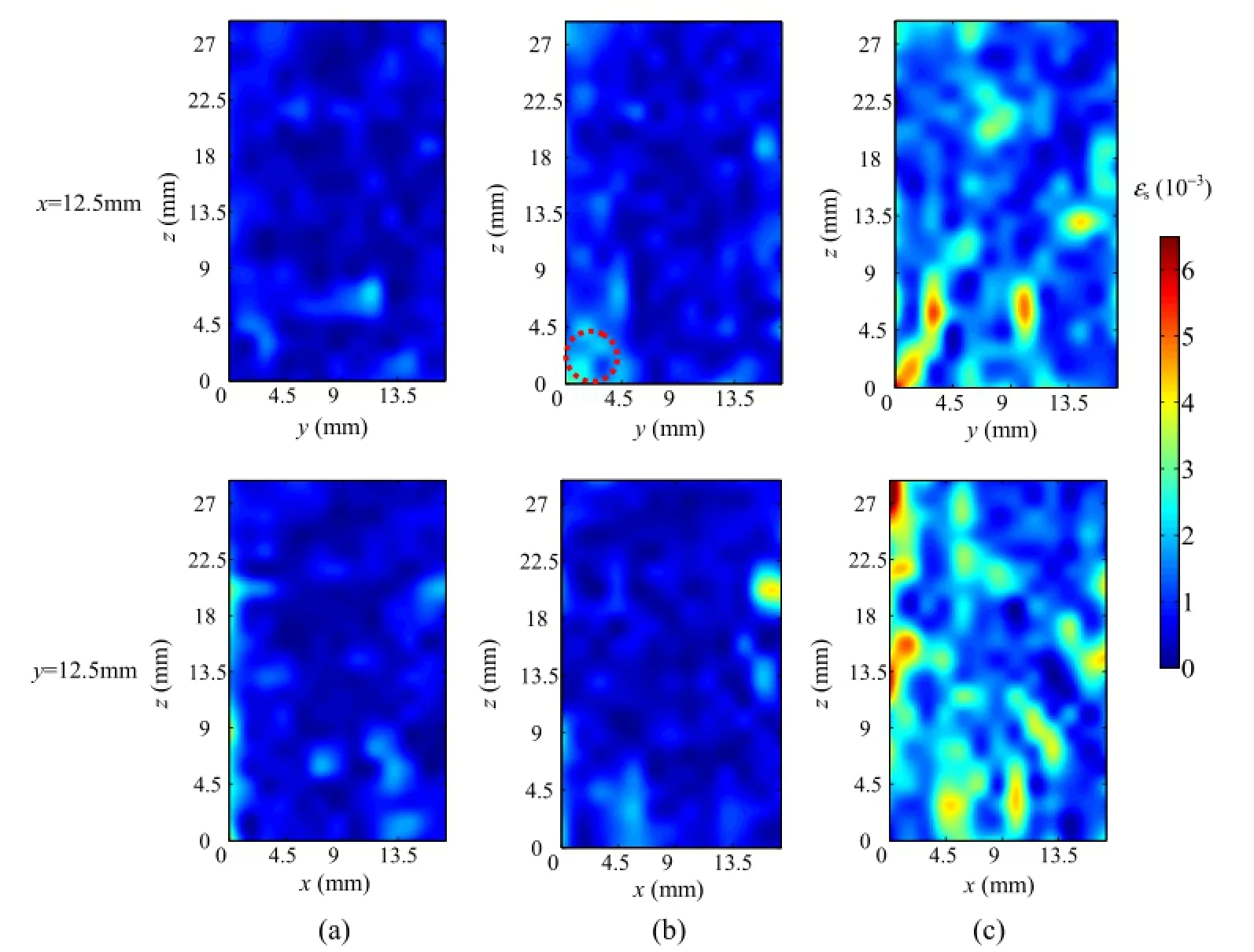
Fig.10.Deviatoric strain3sdistribution of two orthogonal sections at different steps.(a)Step 4(axial stress=6.09 MPa),(b)Step 5(axial stress=7.97 MPa),(c)Step 7(axial stress=11.98 MP).

Fig.11.Volumetric strain3vdistribution of two orthogonal sections at different steps.(a)Step 4(axial stress=6.09 MPa),(b)Step 5(axial stress=7.97 MPa),(c)Step 7(axial stress=11.98 MPa).

We calculate the mean value of the deviatoric strains and the volumetric strains throughout the specimen,and plot their values and the axial stress as a function of the axial strain,as shown in Fig.12.The distributions indicate f ve phases of specimen deformation development.In the f rst compaction phaseAB,thevolumetric strain is negative,indicating that the pre-existing microcracks and pores in the material are being closed.In the elastic phaseBC,the relation between the axial strain and stress is in approximately linear relationship,whereas the volumetric strain decreases and the deviatoric strain becomes higher.At pointC,the volumetric strain value reaches a minimum value.After that,the volumetric strain increases sharply while the deviatoric strain grows in a nonlinear fashion.The stress at pointCis de f ned as the dilation initiation point with a load of 6.07 MPa which is 50.9%of peak load.In the phaseCD,the microcracks smaller than the voxel size(i.e.the spatial resolution limit)of the CT image are being developed,resulting in some discrete strain localization regions shown in upper of Fig.10a with light color.At pointD,the volumetric strain is zero.Beyond pointDthe volumetric strain continues to rise dramatically,indicating that the specimen dilation speed increases.It is reasonable to speculate that,at this stage,the microcracks grow rapidly and eventually coalesce into macrocracks.But the specimen still retains its load-bearing capacity.In the phaseDE,the deviatoric strain also grows rapidly which prompts the development of strain localization regions.We de f ne pointDas the initiation point of a macrocrack(larger than the voxel)as the result of the coalesce of microcracks parallel to the loading direction.The load at pointDis 8.25 MPa which is 68.9%of peak axial load.The phaseEFis the post-peak phase and the specimen fails.

Fig.12.Deviatoric strain and volumetric strain curves.

4.Discussions

4.1.Factors that may affect the accuracy of applying DVSP to red sandstone

4.1.1.The effect of the quality of structure

When measuring 2D surface displacements,it is fairly easy to create a speckle pattern on the surface of a specimen using a variety of methods(Kozicki and Tejchman,2007;Hall et al.,2010a,b; Dautriat et al.,2011;Nguyen et al.,2011;Lin and Labuz,2013; Zhang et al.,2013).However,creating a 3D volumetric speckle pattern is a much more complicated endeavor.One can either arti f cially introduce markers into the studied material(Huang et al.,2011),or just use the material’s internal microstructure itself as the speckle pattern(Bay et al.,1999;Lenoir et al.,2007;Hall et al.,2010a,b;Charalampidou et al.,2011,2014).In this study,we use the natural microstructure of red sandstone as the volumetric speckle pattern.This pattern is not an ideal speckle pattern,thus errors might be introduced.

In Fig.13,the CT scanned cross-sections of red sandstone and medium sandstone are shown in the same magni f cation.For assessing the difference of their structures,we compute the autocorrelation radiusrbased on the autocorrelation function of the CT images.In this study,the autocorrelation radiusris the radius at half height of the normalized autocorrelation function of the CT images(see Fig.13c)(David,2004).The autocorrelation radius of the red sandstone is 1.4 voxels(1 voxel=45μm3),and the autocorrelation radius of medium sandstone is 4.1 voxels.

Two 200 voxel×200 voxel×200 voxel volume images are cropped from the initial volume images of these materials and de f ned as reference images,respectively.The“deformed”volume images are then obtained by the Fourier transform method (Schreier et al.,2000).For simplicity,only a pure rigid body translation is imposed.Ten different sub-voxel displacements ranging from 0.1 voxel to 1.0 voxel are applied along thez-direction,corresponding to a shift of 0.1 voxel between any two successive images.The displacement f elds are all calculated using a 64 voxel×64 voxel×64 voxel subset.The results are depicted in Fig.14.It is noted that the accuracy and precision of the red sandstone are better than those of the medium sandstone.For a smaller autocorrelation radius,there are more speckles contained in each of the subsets,thus improving the performance of DVSP.

Fig.13.CT Images of specimen and normalized autocorrelation function curves.(a) Red sandstone,(b)Medium sandstone,and(c)Associated centered and normalized autocorrelation radius at half height.

4.1.2.The effect of the size of subset

With different sizes of subset,different speckle information is embedded within the subset thus affecting the accuracy of the obtained results.As a demonstration,we crop a block with 200 voxel×200 voxel×200 voxel from the middle part of the volume image of the red sandstone in step 1,and de f ne it as the reference volume image.The“deformed”volume images are obtained by imposing sub-voxel displacements from 0.1 voxel to 1.0 voxel along thez-direction,corresponding to a shift of 0.1 voxel between any two successive images.These volume images with pre-imposed sub-voxel translation are used to investigate the accuracy and precision of DVSP with different subset sizes.The subset sizes areselected as 16 voxel×16 voxel×16 voxel,32 voxel×32 voxel×32 voxel and 64 voxel×64 voxel×64 voxel,respectively,and the overlap between neighboring subsets is half of the subset size. Fig.15 shows the mean bias error and the standard deviation error. It is noted that both the mean bias error and the standard deviation error of DVSP depend on the size of the subset.As the subset size increases,both the accuracy and precision of DVSP are improved. The calculated displacement using a large subset results in a smaller mean bias error as well as a smaller standard deviation error.

In the DVSP theory,the subset is assumed to be rigid.In reality there is deformation and rotation of the material within the subset. While increasing the subset size results in better accuracy of DVSP, the errors caused by ignoring the deformation and rotation of the material within the subset tend to increase too.Thus the selection of the proper subset size has to be judiciously taken.In practical applications,we can use the above-described method of imposing virtual displacements to determine the optimal parameters for DVSP.

Fig.14.Comparisons of two different rock materials.(a)Mean bias error,and(b) Standard deviation.

4.1.3.Baseline test

CT slice images are reconstructed with the appropriate mathematical algorithm from different angular radiographic projections. The non-uniformity of detector elements,the polychromatic nature of X-ray,the imperfect motion of the rotation stage,and the possible rigid body motion of the specimen will all contribute to different artifacts,which will affect the performance of DVSP.

Fig.15.Comparisons among different sizes of subset.(a)Mean bias error,and(b) Standard deviation.

To analyze the effects of the artifacts introduced by the scanner, ACTIS 225/320 Industrial Computed Tomography System,we take a baseline test,in which two consecutive scans of the red sandstone specimen are taken,using identical settings and without moving (other than the tomographic rotation)or deforming the sample. The volume image has the size of 900 voxel×900 voxel×600 voxel,and the physical size of a voxel is 29μm3.Ideally,the displacement f elds computed by DVSP for this pair of volume images should be zero everywhere,but the above factors may affect the results.Table 2 shows the statistic errors.The measurement uncertainty is 0.043 voxel.As can be seen,the displacements are clearly greater than 0.043 voxel standard deviation.This means that the displacements represent an actual rigid motion along three directions,respectively,and are not really noise.This motion,which DVSP is able to capture,is likely to occur because of the tomography rotation stage.In the compression experiment,the errors caused by the above factors are quite small compared with the practical deformation.Therefore,the measurement results are credible.

Besides the above factors,the image contrast also in f uences the measurements.In Mao et al.(2015),all these factors that wouldin f uence the performance of DVSP technique are analyzed in detail.

Table 2Errors caused by artifacts and imperfect motion.

4.2.Computational effciency of DVSP

DVSP and DVC originated from different concepts and evolved differently as well.Compared with DVSP,DVC has only a slightly higher accuracy and precision considering the deformation or the rotation in the subset,but it consumes much more calculation time. For a search region of sizen,which is equal to the subset size,the computational complexity for searching using FFT isO（2n3log10n）, whereas in the case of DVC the searching in the spatial domain isO（n6）,clearly demonstrating the computational ef f ciency of the DVSP algorithm.This advantage is magni f ed when high-resolution and high-volume images are processed as is the case in most practical problems.

In this study,DVSP is coded with MATLAB.The computation is performed on HP workstation Z420 with Intel Xeon E5-1650 3.2 12 M 1600 6C CPU,32 GB DDR3-1600 ECC RAM memory.The calculated volumetric image has a dimension of 566 voxel×566 voxel×801 voxel,the size of subset is 64 voxel×64 voxel×64 voxel and overlap is 32 voxels.It takes 9157 s to calculate overall images.For each subset,the calculation time is 1.49 s.If we would use the unoptimized DVC method with the size of subset being 51 voxel×51 voxel×51 voxel,overlap 25 voxels,and search area 17 voxel×17 voxel×17 voxel,it will takes 1,172,790 s to calculate.For each subset,the calculation time would be 88.6 s.It is nearly 60 times longer than using DVSP.Several approaches have been proposed to reduce redundancy and improve the ef f ciency of DVC(Pan et al.,2012;Huang et al.,2011;Gates et al.,2011),but the implementation complexity increases as well.

5.Conclusions

In this study,X-ray scanning in situ is conducted to investigate the damage and failure process of red sandstone specimen under uniaxial compression tests.Analysis of 3D full-tensor strain f elds, derived from the DVSP displacement f elds,has revealed the pattern of strain localization during loading,and then subsequent initiation of the crack inside the localized zone resulting in failure of specimen.

The advantage of DVSP is its high computational ef f ciency.In practical applications,millions of points would be calculated.The time-saving feature of DVSP is of considerable advantage.In this study,we just make a tentative attempt to the application of DVSP, and there is much more to do to improve the performance.We foresee the technique to have wide applications in rock mechanics.

Con f ict of interest

The authors wish to con f rm that there are no known con f icts of interest associated with this publication and there has been no signi f cant f nancial support for this work that could have in f uenced its outcome.

Acknowledgments

This work is f nancially supported by National Basic Research Program of China(973 Program)(No.2010CB732002),National Natural Science Foundation of China(Nos.51374211,51374215), National Key Foundation for Exploring Scienti f c Instrument of China(No.2013YQ240803),Fundamental Research Funds for the Central Universities(No.2009QM02)and the Laboratory for Experimental Mechanic Research of the Department of Mechanical Engineering at Stony Brook University.F.P.Chiang wishes to thank Dr.Yapa Rajapakse,Director of the US Of f ce of Naval Research’s Solid Mechanics Program for his support over the years for advancement of the speckle technique.

Adam J,Schreurs G,Klinkmuller M,Wieneke M.2D/3D strain localization and fault simulation in analogue experiments:insights from X-ray computed tomography and tomographic image correlation.Bollettino di Geo f sica Teorica ed Applicata 2008;49(Supp.2):21-2.

Adam J,Klinkmuller M,Schreurs G,Wieneke B.Quantitative 3D strain analysis in analogue experiments simulating tectonic deformation:integration of X-ray computed tomography and digital volume correlation techniques.Journal of Structural Geology 2013;55:127-49.

Alshibli KA,Sture S,Costes NC,Frank ML,Lankton MR,Batiste SN,Swanson RA. Assessment of localized deformation in sand using X-ray computed tomography.Geotechnical Testing Journal 2000;23(3):274-99.

Amitrano D.Rupture by damage accumulation in rocks.International Journal of Fracture 2006;139(3-4):369-81.

Bay BK,Smith TS,Fyhie DP,Saad M.Digital volume correlation:three-dimensional strain mapping using X-ray tomography.Experimental Mechanics 1999;39(3): 217-26.

Bésuelle P,Desruesb J,Raynaudc S.Experimental characterisation of the localisation phenomenon inside a vosges sandstone in a triaxial cell.International Journal of Rock Mechanics and Mining Sciences 2000;37(8):1223-37.

Charalampidou EM,Hall SA,Stanchits S.Characterization of shear and compaction bands in a porous sandstone deformed under triaxial compression.Tectonophysics 2011;503(1-2):8-17.

Charalampidou EM,Hall SA,Stanchits S,Viggiani G,Lewis H.Shear-enhanced compaction band identi f cation at the laboratory scale using acoustic and fullf eld methods.International Journal of Rock Mechanics and Mining Sciences 2014;67:240-52.

Chiang FP,Mao LT.Development of interior strain measurement techniques using random speckle patterns.Meccanica 2015;50(2):401-10.

Dautriat J,Bornert M,Gland N,Dimanov A,Raphanel J.Localized deformation induced by heterogeneities in porous carbonate analysed by multi-scale digital image correlation.Tectonophysics 2011;503(1-2):100-16.

David MR.A simple autocorrelation algorithm for determining grain size from digital images of sediment.Journal of Sedimentary Research 2004;74(1): 160-5.

Desrues J,Chambon R,Mokni M,Mazerolle F.Void ratio evolution inside shear bands in triaxial sand specimens studied by computed tomography.Geotechnique 1996;46(3):529-46.

Desrues J,Viggiani G.Strain localization in sand:an overview of the experimental results obtained in grenoble using stereophotogrammetry.International Journal of Numerical Analytical Methods in Geomechanics 2004;28(4): 279-321.

Gates M,Lambros J,Heath MT.Towards high performance digital volume correlation.Experimental Mechanics 2011;51(4):491-507.

Hall SA,Wood DM,Ibraim E,Viggiani G.Localised deformation patterning in 2D granular materials revealed by digital image correlation.Granular Matter 2010a;12(1):1-14.

Hall SA,Bornert M,Desrues J,Pannier Y,Lenoir N,Viggiani G,Bésuelle P.Discrete and continuum analysis of localised deformation in sand using X-rayμCT and volumetric digital image correlation.Geotechnique 2010b;60(5):315-22.

Huang JY,Pan XC,Li SS.A digital volume correlation technique for 3D deformation measurements of soft gels.International Journal of Applied Mechanics 2011;3(2):335-54.

Kozicki J,Tejchman J.Experimental investigations of strain localization in concrete using digital image correlation(DIC)technique.Archives of Hydro-Engineering and Environmental Mechanics 2007;54(1):3-24.

Lenoir N,Bornert M,Desrues J,Bésuelle P,Viggiani G.Volumetric digital image correlation applied to X-ray microtomography images from triaxial compression tests on argillaceous rock.Strain 2007;43(3):193-205.

Lin Q,Labuz JF.Fracture of sandstone characterized by digital image correlation.International Journal of Rock Mechanics and Mining Sciences 2013;60: 235-45.

Louis L,Wong T,Baud P,Tembe S.Imaging strain localization by X-ray computed tomography:discrete compaction bands in Diemelstadt sandstone.Journal of Structural Geology 2006;28(5):762-75.

Louis L,Wong T,Baud P.Imaging strain localization by X-ray radiography and digital image correlation:deformation bands in Rothbach sandstone.Journal of Structural Geology 2007;29(1):129-40.

Mao LT,Chiang FP,Yuan ZX.3D displacement measurement in solid using digital volumetric speckle photography and computer tomography.Acta Optica Sinica 2015;35(3):0312001.

Nguyen TL,Hall SA,Vacher P.Fracture mechanisms in soft rock:identi f cation and quanti f cation of evolving displacement discontinuities by extended digital image correlation.Tectonophysics 2011;503(1-2):117-28.

Pan B,Wu DF,Wang ZY.Internal displacement and strain measurement using digital volume correlation:a least-squares framework.Measurement Science and Technology 2012;23(4):45002.

Pan B,Asundi A,Xie HM,Gao JX.Digital image correlation using iterative least squares and pointwise least squares for displacement f eld and strain f eld measurements.Optical Lasers Engineering 2009;47(7-8):865-74.

Schreier HW,Braasch JR,Sutton MA.Systematic errors in digital image correlation caused by intensity interpolation.Optical Engineering 2000;39(11):2915-21.

Suzanne R,Dominique NT,Jacques D,Mazerolle F.Brittle-to-ductile transition in Beaucaire marl from triaxial tests under the CT-scanner.International Journal of Rock Mechanics and Mining Sciences 2008;45(5):653-71.

Viggiani G,Lenoir N,Bésuelle P,Michiel MD,Marello S,Desrues J,Kretzschmer M.X-ray microtomography for studying localized deformation in f ne-grained geomaterials under triaxial compression.Comptes Rendus Mécanique 2004;332(10):819-26.

Zhang H,Huang GY,Song HP,Kang YL.Experimental characterization of strain localization in rock.Geophysical Journal International 2013;194(3):1554-8.

Lingtao Mao,born in Shihezi,Xinjiang Uygur Autonomous Region,China,is an Associate Professor at State Key Laboratory of Coal Resources and Safe Mining(China University of Mining&Technology(Beijing)),and an Adjunct Research Associate Professor in the Department of Mechanical Engineering at the State University of New York at Stony Brook,U.S.A.He got the BE at Jilin University of Technology,and the M.Sc.and Ph.D.in Engineering Mechanics at China University of Mining&Technology(Beijing)in 2002 and 2005,respectively.From June 2012 to May 2013,he joined the Department of Mechanical Engineering at the State University of New York at Stony Brook, U.S.A,as a visiting scholar.His current research interests include the development and application of photomechanics on rocks and composites.He is the author or co-author of more than f fty scienti f c papers and ten patents.

*Corresponding author.Tel.:+86 10 82386706.

E-mail address:mlt@cumtb.edu.cn(L.Mao).

Peer review under responsibility of Institute of Rock and Soil Mechanics, Chinese Academy of Sciences.

1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2015.01.003