Understanding the microscopic moisture migration in pore space using DEM simulation

Yuan Guo,Xiong(Bill)Yu

Department of Civil Engineering,Case Western Reserve University,10900 Euclid Avenue,Cleveland,OH 44106,USA

Understanding the microscopic moisture migration in pore space using DEM simulation

Yuan Guo,Xiong(Bill)Yu*

Department of Civil Engineering,Case Western Reserve University,10900 Euclid Avenue,Cleveland,OH 44106,USA

A R T I C L E I N F O

Article history:

Received 26 December 2014

Received in revised form

4 March 2015

Accepted 6 March 2015

Available online 20 March 2015

Moisture migration

Consolidated undrained triaxial test

Particle chains

Porosity distribution

Pore water pressure

The deformation of soil skeleton and migration of pore f uid are the major factors relevant to the triggering of and damages by liquefaction.The in f uence of pore f uid migration during earthquake has been demonstrated from recent model experiments and f eld case studies.Most of the current liquefaction assessment models are based on testing of isotropic lique f able materials.However the recent New Zealand earthquake shows much severer damages than those predicted by existing models.A fundamental cause has been contributed to the embedded layers of low permeability silts.The existence of these silt layers inhibits water migration under seismic loads,which accelerated liquefaction and caused a much larger settlement than that predicted by existing theories.This study intends to understand the process of moisture migration in the pore space of sand using discrete element method(DEM)simulation.Simulations were conducted on consolidated undrained triaxial testing of sand where a cylinder sample of sand was built and subjected to a constant con f ning pressure and axial loading.The porosity distribution was monitored during the axial loading process.The spatial distribution of porosity change was determined,which had a direct relationship with the distribution of excess pore water pressure.The non-uniform distribution of excess pore water pressure causes moisture migration.From this,the migration of pore water during the loading process can be estimated.The results of DEM simulation show a few important observations:(1)External forces are mainly carried and transmitted by the particle chains of the soil sample;(2)Porosity distribution during loading is not uniform due to nonhomogeneous soil fabric(i.e.the initial particle arrangement and existence of particle chains);(3) Excess pore water pressure develops differently at different loading stages.At the early stage of loading, zones with a high initial porosity feature higher porosity changes under the in f uence of external loading, which leads to a larger pore pressure variation(increase or decrease)in such zones.As the axial strain increases,particle rearrangement occurs and f nal porosity distribution has minor relationship with the initial condition,and the pore pressure distribution becomes irregular.The differences in the pore pressure development imply that water will migrate in the pore space in order to balance the pore water pressure distribution.The results of this simulation offer an insight on the microscale water migration in the soil pore space,which is important for holistic description of the triggering of soil liquefaction in light of its microstructure.

©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

Soil liquefaction,which leads to substantial losses of soil stiffness and strength,can cause catastrophic damages to the superstructures.Most of the current liquefaction assessment models are based on the assumption of isotropic lique f able materials. However,the recent New Zealand earthquake shows a much severer damage than expected.Researches have also shown that migration of water in sand is an important factor triggering soil liquefaction(Dashti et al.,2010a,2010b;Maharjan and Takahashi, 2013,2014).The ground settlement is not proportional to the thickness of lique f able layers as predicted by existing models (Dashti et al.,2010b).

Understanding soil-water interactions can provide a new insight on the liquefaction mechanism,which has aroused signi fcant interest in the research community.In static condition,water migration in soil was found to behave non-linearly during experiment(Wang et al.,2013a).For hydrophobic soil contaminated by oil,there is a critical moisture content,beyond which it behaves as hydrophilic soil(Quyum et al.,2002).Oscillating water pressurewas found to have a signi f cant effect on liquefaction of sand(Lu and Cui,2004).For non-uniform sand,the pore pressure and the skeleton strain raise rapidly in low permeability areas.Centrifuge tests also indicate that the soil permeability plays an important role in pore water pressure development during and after liquefaction (Wang et al.,2013b).Models based on strain energy have been proposed to describe the liquefaction process(Jafarian et al.,2012). These researches show that moisture migration and soil particle deformation determine the macroscopic mechanical responses of sand.

Bray’s centrifuge test explicitly demonstrates the importance of moisture migration in triggering sand liquefaction(Dashti et al., 2010a).By installing an impermeable water barrier underneath a model building to prevent water migration but allow shear deformation,the settlement was reduced by over 25%compared with the condition when moisture migration is allowed.This clearly demonstrates the crucial role of moisture migration in soil liquefaction.The discontinuous layered soil deposits can also in f uence the pore water migration,for example,as observed in the experiments conducted by Takahashi(Maharjan and Takahashi,2013).In the centrifuge model,the pore water was found to be trapped beneath the low permeability silty sand,and it took a long period for the excess pore water pressure to dissipate.This also leads to non-uniform settlement of the upper structure.

The thermally induced water migration has been discussed theoretically and veri f ed with experiments(Liu et al.,2013).The variation of pore pressure up to 40 kPa was observed in sand sample during freezing-thawing test(Zhang et al.,2014).For dynamic response,the coupled method,which considers both the solid particles and f uid f eld,provides a good understanding of the process of liquefaction(El Shamy and Abdelhamid,2014).Researches show that liquefaction can be explained by the reduction in void space during shaking that leads to accumulation of pore water pressure.

In this paper,discrete element method(DEM)was used to understand the mechanism of moisture migration during a static consolidated undrained triaxial test.The pore pressure distribution in the sand sample was estimated by monitoring the spatial variations of porosity during the loading process.

2.A DEM model for consolidated undrained triaxial test

A computational model was built for consolidated undrained shear test with a diameter of 50 mm and height of 100 mm.Table 1 shows the partial parameters and mechanical properties of sand. The particle radii range from 1.5 mm to 2.5 mm with a uniform distribution(Fig.1).The con f ning pressure is set to be 100 kPa. Strain-controlled loading was assumed where the upper wall moves downward with a constant velocity.The loading rate was determined via a sensitivity study on the loading velocity.The results show that below a certain velocity value(i.e.7.5 mm/s),the mechanical responses are very much similar.Based on this observation,loading velocity of 7.5 mm/s was used in the simulations,which corresponds to a strain rate of 7.5%/s.

The deformation of soil particles results from the effective stress among particles.To describe the macro mechanical responses of the sand sample under loading,the pore water pressure development in this model was determined.The pore water pressure is estimated by the change of volumetric strain among the sand particles.The compressibility of water-air mixture can be calculated through the equation below(Fredlund,1976;Fredlund and Rahardjo,1993):

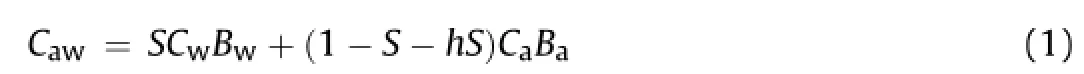
Table 1Particle parameters and mechanical properties of sand.

Fig.1.DEM model and particle size distribution curve.

whereCawis the compressibility of air-water mixture(kPa-1);Sis the degree of saturation;Cwis the compressibility of water,which equals 4.58×10-7kPa-1;his the solubility of air in water, expressed as ratio of absorbed air volume to water volume;BwandBaare pore-water and pore-air pressure coef f cients for isotropic loading,both of which are assumed to be 1.0.

According to Henry’s Law,the air dissolved in water is proportional to the air pressure.The solubility of air in water at 20°C under a pressure of 202 kPa is 0.037.It is very dif f cult to acquire a fully saturated sample in the f eld or laboratory conditions.Researches show that the degree of saturation of saturated soil varies from 85%to 95%in the f eld and laboratory conditions (Faybishenko,1995;Fry et al.,1997;Holocher et al.,2002; Sakaguchi et al.,2005).In this model,we assume the quasi-saturated soil with a degree of saturation of 90%.This corresponds to compressibility of air-water mixture of 6.58×10-4kPa-1.The pore water pressureuwas calculated during each time step using Eq.(2).The con f ning pressure,which is the sum of effective stress and pore water pressure,is assumed to maintain constant using the servo control.

where εvis the volumetric strain of soil sample.

3.Simulation results

During loading,particles in the DEM model are subjected to the effective stress,and the pore pressure distribution is calculated from the porosity distribution.The coupling process is based on two assumptions:(1)reaction forces on soil particles due to water migration are negligible;and(2)water migration completes in each time step.

The simulated loading curves for the total stress and effective stress are shown in Figs.2 and 3,respectively.The effective stresses are determined directly from the numerical model simulations.Thelarger effective stress than total stress indicates the development of a negative pore pressure.

The simulation results indicated that when the sample is subjected to axial load(εa＜0.005),the volumetric strain decreases slightly and then increases dramatically.This indicates that a shear dilation occurs in most time.The average pore water pressure of the whole sample is plotted in Fig.4.The increase of volumetric strain leads to generation of negative pore pressure in the f uid f eld,and therefore the effective stress on soil increases during the loading process(Fig.3).

Fig.2.Total stress curves during loading.

4.Contact forces among particles

The normal and shear contact forces among particles are obtained.Each contact consists of two types of contacting entities, particle-particle contact or particle-wall contact.Among the 3808 particles,a total of 8228 contacts are generated.These contacts provide normal or shear forces if two particles have normal or tangential relative motions.

The contact forces range from 0 N to 43 N when the axial strain3aequals 17%.Despite of this large range in the magnitude of contact force,the majority of contact forces are in the small ends.A cumulative distribution curve for normal contact forces is plotted in Fig.5.It describes the distribution of the magnitude of normalcontact forces among particles.For example,80%of the normal contact forces are smaller than 8 N,and 95%of the normal contact forces lie within 15 N.Large normal contact forces only occur among a very small amount of particles.

Fig.3.Effective stress curves during loading.

Fig.4.Pore water pressure curve during loading.Negative value means traction.

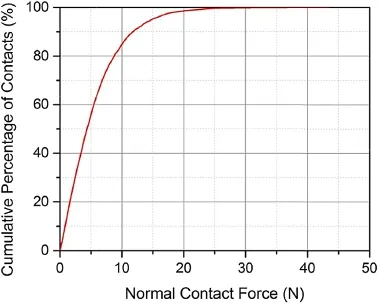
Fig.5.Cumulative percentage curve of normal contact forces.

Fig.6.Cumulative percentage curve of shear contact forces.

The shear contact forces show a similar phenomenon(Fig.6). While the maximum shear contact force reaches 9 N,more than 95%of shear contact forces are smaller than 3 N.

The spatial distribution of contact forces is plotted in Fig.7.It shows that the contact forces are not uniformly distributed among particles.The external forces are transmitted along granular chains formed within the soil skeleton(Santamarina,2001).Particles within the granular chains tend to be subjected to larger forces. Formation of granular chains depends largely on the particle arrangement,particle size,initial condition,etc.The overall soil deformation is mainly determined by the deformation of granular chains of the soil skeleton.For particles lying outside of the granular chains,the contact force and deformation are much smaller. This non-uniform distribution of both contact force and deformation leads to a non-uniform development of volumetric strain. Consequently,for saturated soil,pore water pressure will be quite different at different locations when subjected to external loading.

As discussed in the previous context,although the maximum contact force is 43 N,only 5%of particles are subjected to forces larger than 15 N.These particles with normal contact forces larger than 15 N are plotted in Fig.8.It clearly shows the transfer of external forces through the soil skeleton.Since the bottom wall is a f xed end,the load transferring routes at the bottom of sample are obviously concentrated on a few spots.

Fig.9 plots the average contact forces vs.particle sizes.It shows that the average contact forces of larger particles tend to be larger than that of smaller ones.As the radii vary from 1.5 mm to 2.5 mm, the average contact forces increase by 140%from 4.5 N to 10.8 N.If we normalize the contact forces by dividing by their corresponding particle hemisphere areas,as shown in Fig.10,particles with a smaller radius are subjected to equal or even larger stress compared with large particles.As a quick note,there are somesmall-sized particles detached from their surroundings,which may also cause the smaller average contact force.All these discussions show that contact forces for small-sized particles are small but the stress in the particles is not negligible.

Fig.7.Contact forces(normal and shear)among particles.

Fig.8.Particles with contact forces larger than 15 N.

Fig.9.Average contact forces vs.different particle sizes.

Fig.10.Normalized stress vs.different particle sizes.

Fig.11.Porosity distribution at different axial strains.

Fig.12.Pore water pressure distribution at different axial strains(unit:Pa).

Table 2Fluid velocities based on Darcy’s Law.

5.Pore pressure distribution

The porosity distribution during loading is determined from computational simulations(Fig.11).Before the loading begins,soil sample is only subjected to con f ning pressure.However,the porosity distribution is quite non-uniform and varies from 0.33 to 0.37.When the axial strain increases,zones with high porosities deform signi f cantly.These deformations cause large increases of porosity in these areas.As the axial strain increases to 0.06,particle rearrangement occurs and porosity distribution changes signi fcantly.The f nal porosity distribution has little relationship with the initial condition.

The permeability of medium sand is relatively high and water migration,even under a low pressure gradient,can be quite rapid. Assuming that water migration completes at the end of each time step,by calculating the change of volumetric strains at different locations,we can determine the distribution of pore water pressure at different times,as shown in Fig.12.The black arrows represent the main migrating routes of water.

The direction of water migration concurs well with the porosity distribution.At the early stage,particle deformations are highly related to the initial condition.As the zones with higher porosities keep bulging,extra water f ows into these areas,as shown in Fig.12a-c.However,under large strain conditions,particle rearrangement occurs and particles within soil chains produce much larger deformations.Corresponding to the random distribution of the particle chains,the routes of water migration also show irregularity.

Using the Darcy’s Law,the migration velocity of f uid during the testing process can be estimated.The coef f cient of permeability for clean sand is chosen as 5×10-3cm/s(West,1995).The pore pressure and porosity can be determined directly from the model. The maximum f uid velocities at different axial strains are calculated and shown in Table 2.

In general,the velocity of f ow migration increases with strain levels.

6.Conclusions

Fluid migration has been identi f ed as an important process responsible for damages due to liquefaction.To understand the process of moisture migration,a model for triaxial test has been built using DEM to simulate the microscopic phenomena during consolidated undrained shear test.The f uid pressure was calculated by considering the change of volumetric strain during loading.

The results of contact forces show that external forces are transmitted through soil skeletons inside the soil sample.Particles inside the particle chains tend to have larger contact forces.Although the maximum contact force can be as large as 43 N,95%of the total particles are subjected to the forces smaller than 15 N.It also shows that large particles typically have large contact forces.But stress in the particles due to contact forces is generally higher in smaller particles.

The simulation model predicted uneven distribution of porosity during loading conditions.This non-uniform distribution comes from two sources:the initial anisotropic property of soil sample from particle generation,and the randomly distributed soil skeletons.At low axial strain conditions(εa＜0.06),porosity increases signi f cantly in zones with a large initial porosity.As the axial strain further increases,particle rearrangement occurs and the porosity distribution becomes random.

The simulation also indicates that under external loading,the change of pore space leads to a redistribution of pore water pressure.The direction of water migration is consistent with the variation of porosity.At the initial loading stage,water migrates into areas with high porosity.As the axial strain further increases,the direction of water migration becomes more randomly oriented.

Overall,the simulation provides insight on the migration of water in the pore space,an important process determining the responses of saturated soils under loading.The process of simulation will be further extended to more complex loading conditions.

Con f ict of interest

The authors wish to con f rm that there are no known con f icts of interest associated with this publication and there has been no signi f cant f nancial support for this work that could have in f uenced its outcome.

Fredlund DG,Rahardjo H.Soil mechanics for unsaturated soils.Wiley-Interscience; 1993.

Fredlund DG.Density and compressibility characteristics of air-water mixtures. Canadian Geotechnical Journal 1976;13(4):386-96.

Fry VA,Selker JS,Gorelick SM.Experimental investigations for trapping oxygen gas in saturated porous media for in situ bioremediation.Water Resources Research 1997;33(12):2687-96.

Holocher J,Peeters F,Aeschbach-Hertig W,Hofer M,Brennwald M,Kinzelbach W, Kipfer R.Experimental investigations on the formation of excess air in quasisaturated porous media.Geochimica et Cosmochimica Acta 2002;66(23): 4103-17.

Jafarian Y,Towhata I,Baziar MH,Noorzad A,Bahmanpour A.Strain energy based evaluation of liquefaction and residual pore water pressure in sands using cyclic torsional shear experiments.Soil Dynamics and Earthquake Engineering 2012;35:13-28.

Liu Z,Zhang B,Yu X,Tao J,Sun Y,Gao Q.Thermally induced water f ux in soils. Journal of Transportation Research Record 2013;2349:63-71.

Lu X,Cui P.The liquefaction and displacement of highly saturated sand under water pressure oscillation.Ocean Engineering 2004;31(7):795-811.

Maharjan M,Takahashi A.Centrifuge model tests on liquefaction-induced settlement and pore water migration in non-homogeneous soil deposits.Soil Dynamics and Earthquake Engineering 2013;55:161-9.

Maharjan M,Takahashi A.Liquefaction-induced deformation of earthen embankments on non-homogeneous soil deposits under sequential ground motions. Soil Dynamics and Earthquake Engineering 2014;66:113-24.

Quyum A,Achari G,Goodman RH.Effect of wetting and drying and dilution on moisture migration through oil contaminated hydrophobic soils.The Science of the Total Environment 2002;296(1-3):77-87.

Sakaguchi A,Nishimura T,Kato M.The effect of entrapped air on the quasisaturated soil hydraulic conductivity and comparison with the unsaturated hydraulic conductivity.Vadose Zone Journal 2005;4(1):139-44.

Santamarina JC.Soil behavior at the microscale:particle forces.In:Germaine JT, Sheahan TC,Whitman RV,editors.Soil behavior and soft ground construction: proceedings of the symposium;2001.p.25-56.

Wang B,Zen K,Chen GQ,Zhang YB,Kasama K.Excess pore pressure dissipation and solidi f cation after liquefaction of saturated sand deposits.Soil Dynamics and Earthquake Engineering 2013b;49:157-64.

Wang MW,Li J,Ge S,Li ST.Moisture migration tests on unsaturated expansive clays in Hefei,China.Applied Clay Science 2013a;79:30-5.

West TR.Geology applied to engineering.Prentice Hall;1995.

Zhang L,Ma W,Yang C,Yuan C.Investigation of the pore water pressures of coarsegrained sandy soil during open-system step-freezing and thawing tests.Engineering Geology 2014;181:233-48.

Dashti S,Bray JD,Pestana JM,Riemer M,Wilson D.Centrifuge testing to evaluate and mitigate liquefaction-induced building settlement mechanisms.Journal of Geotechnical and Geoenvironmental Engineering 2010a;136(7):918-29.

Dashti S,Bray JD,Pestana JM,Riemer M,Wilson D.Mechanisms of seismically induced settlement of buildings with shallow foundations on lique f able soil.Journal of Geotechnical and Geoenvironmental Engineering 2010b;136(1):151-64.

El Shamy U,Abdelhamid Y.Modeling granular soils liquefaction using coupled lattice Boltzmann method and discrete element method.Soil Dynamics and Earthquake Engineering 2014;67:119-32.

Faybishenko BA.Hydraulic behavior of quasi-saturated soils in the presence of entrapped air:laboratory experiments.Water Resources Research 1995;31(10): 2421-35.

Dr.Xiong Yuis working as an associate professor at Case Western Reserve University,USA.His research interests cover geotechnical and infrastructure engineering,environmental geotechnology,foundation engineering,nondestructive testing,sensor technology for infrastructure, environment and energy applications,multi-scale model of civil engineering material and system,computer-aided design,green design,sustainable engineering,etc.

*Corresponding author.Tel.:+1 2163686247.

E-mail address:xiong.yu@case.edu(X.(Bill)Yu).

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2015.03.004