Deformation and failure mechanism of slope in three dimensions

Yingfa Lu

School of Civil Engineering,Hubei University of Technology,Wuhan,430068,China

Deformation and failure mechanism of slope in three dimensions

Yingfa Lu*

School of Civil Engineering,Hubei University of Technology,Wuhan,430068,China

A R T I C L E I N F O

Article history:

Received 23 October 2014

Received in revised form

5 February 2015

Accepted 12 February 2015

Available online 16 March 2015

Failure mechanism

New joint constitutive model(JCM)

Stability analyses

Boundary method by sliding surface

Understanding three-dimensional(3D)slope deformation and failure mechanism and corresponding stability analyses are crucially important issues in geotechnical engineering.In this paper,the mechanisms of progressive failure with thrust-type and pull-type landslides are described in detail.It is considered that the post-failure stress state and the pre-peak stress state may occur at different regions of a landslide body with deformation development,and a critical stress state element(or the soil slice block)exists between the post-failure stress state and the pre-peak stress state regions.In this regard, two sorts of failure modes are suggested for the thrust-type and three sorts for pull-type landslides, based on the characteristics of shear stress and strain(or tensile stress and strain).Accordingly,a new joint constitutive model(JCM)is proposed based on the current stability analytical theories,and it can be used to describe the mechanical behaviors of geo-materials with softening properties.Five methods,i.e. CSRM(comprehensive sliding resistance method),MTM(main thrust method),CDM(comprehensive displacement method),SDM(surplus displacement method),and MPM(main pull method),for slope stability calculation are proposed.The S-shaped curve of monitored displacement vs.time is presented for different points on the sliding surface during progressive failure process of landslide,and the relationship between the displacement of different points on the sliding surface and height of landslide body is regarded as the parabolic curve.The comparisons between the predicted and observed load-displacement and displacement-time relations of the points on the sliding surface are conducted.The classi f cation of stable/unstable displacement-time curves is proposed.The de f nition of the main sliding direction of a landslide is also suggested in such a way that the failure body of landslide(simpli f ed as“collapse body”)is only involved in the main sliding direction,and the strike and the dip are the same as the collapse body.The rake angle is taken as the direction of the sum of sliding forces or the sum of displacements in collapse body,in which the main slip direction is dependent on progressive deformation.The reason of non-convergence with f nite element method(FEM)in calculating the stability of slope is also numerically analyzed,in which a new method considering the slip surface associated with the boundary condition is proposed.It is known that the boundary condition of sliding surface can be described by perfect elasto-plastic model(PEPM)and JCM,and that the stress and strain of a landslide can be described properly with the JCM.

©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

Stability analysis of slope has attracted a great attention for a very long period of time,and great achievements have been made. Some numerical analytical methods are proposed,e.g.the ordinary method,the simpli f ed Bishop method,the Janbu method,the Fellenius method,the Morgenstern method,the strength reduction method(SRM)of f nite element method(FEM)for slope stability analysis.

The limit equilibrium method using rigid block is widely used in engineering.With the development of numerical analysis and computer capability,many researchers try to improve various calculation methods for slope stability analyses,for instances,the three-dimensional(3D)regular limit equilibrium equations(Liu et al.,2007;Zhu and Qian,2007;Li and Qian,2010;Guo et al., 2011)in which six equilibrium conditions are satis f ed.In their study,the whole sliding body was concerned and the stresses of sliding surface were corrected(Zheng,2000,2007;Yao et al.,2001; Liu et al.,2002;Yin et al.,2002;Wang,2004;Zhang et al.,2005;Lu et al.,2010;Zheng et al.,2013)by using an algebraic eigenvalue to solve the problem of non-convergence numerical calculation of the 3D regular limit equilibrium equations.

The above-mentioned methods for slope stability analysis are basically based on the critical stress state(or the limit equilibrium state).The critical stress state refers to the possible failure of slope occurring along the entire slip surface where a critical state is reached simultaneously,thus the critical stress state is considered to be a peak-stress state.The fundamental properties of the thrusttype and pull-type landslides are studied,and it is commonly acknowledged that the post-failure stress states are located in the posterior or front region and the pre-peak stress state is situated at the front or posterior part of landslide for the thrust-type and pulltype landslide,respectively.Only one point(for two-dimensional, 2D)or one curve(for 3D)is under the critical stress state.In this regard,this point or curve is de f ned as the“critical stress state”, which changes from the non-failure state to failure state with progressive deformation.Actually,the failure of landslide takes place progressively,e.g.some zones are under the post-failure stress state,local zone under the critical stress state,and the others under the pre-peak stress state.It can be noted that large deformation occurs in the post-failure stress state,and small deformation is observed in the zone of pre-peak stress state of landslide.In view of landslide deformation,the mechanical parameters at the peak stress state for entire sliding surface have no physical meanings(except the critical stress state),even for the isotopic and homogeneous landslide.The mechanical parameters at the critical stress state can only describe the behaviors of a point (for 2D case)or of a curve(for 3D case)of the sliding surface, suggesting that the above-mentioned methods describing the stability factor are in a sense only the empirical methods for landslide (Lu et al.,2007,2008,2012,2013,2014).

In this paper,two failure modes are proposed for the thrust-type landslide,i.e.type I(failure occurs basically along the weak layer) and type II(failure happens in the posterior region along the weak layer and in the front region along the landslide body);whilst three failure modes are suggested for the pull-type landslide,i.e.type I (the shear failure occurs along the weak layer merely),type II(the shear failure happens in the front region along the weak layer and in the posterior part along the landslide body),and type III(the shear failure occurs in the front region along the weak layer and the pull failure happens in the sliding mass).These failure modes are controlled by shearing behaviors of soft interlayer or by shearing and pulling properties of slip body.For the thrust-type landslide, the critical stress state point(or curve)moves gradually from the posterior to the front region,and for the pull-type landslide,it transfers from the front region to the posterior.In other words,the landslide failure will continue to induce the new critical stress state and the post-failure state.The whole process curve between load (T)and displacement(S)is also divided into types I,II and III,based on which the stability along the sliding surface is divided into stable,less stable and unstable regions,respectively.A new joint constitutive model(JCM)is suggested which can describe the mechanical behaviors of types I and III,and its mechanical parameters can be calibrated accordingly.The relationships between displacement(S)of monitoring points on sliding surface and time (t)are employed for thrust-type and pull-type landslides.The S-shaped curve is suggested to describe the relation betweenSandtof the monitoring points on the sliding surface.Different S-shaped curves are presented for separated points on the sliding surface at a time.The relationship betweenSandtis classi f ed into two types, i.e.type I(steady displacement-time curve)and type II(unsteady displacement-time curve).This classi f cation is related to the mechanical properties of the whole process between load and displacement.The characteristic of the parabolic curve exists between displacement of different points on the sliding surface and height of landslide body,which varies with deformations and can be used to predict the landslide failure.The stability factors obtained by the traditional calculating methods are compared under different stress states.The maximum stability factor occurs under the critical stress state and the minimum under the residual stress state if the same method is employed.Its value varies from the maximum to the minimum,dependent on the stress states in which the sliding surface is located,i.e.the critical stress state,postfailure stress state or residual stress state.Basically,several methods are suggested to evaluate the stability of landslide,for instance,the comprehensive sliding resistance method(CSRM), main thrust method(MTM),comprehensive displacement method (CDM),surplus displacement method(SDM),and main pull method (MPM).The SRM is usually employed by the FEM,but it is not suitable for comparing the obtained stress and strain f elds with those in f eld when the strength reduction coef f cient(F)is not equal to 1.The cause of non-convergence in SRM analysis can be attributed to the different deformation values among the sliding body,varying stiffness of sliding surface and sliding bed,different strength reduction,and large deformation in local region.A new method,sliding surface boundary method(SFBM),is proposed associated with FEM.A perfect elasto-plastic model(PEPM)or JCM can be used to describe the mechanical behaviors of the sliding surface.It is proven that the PEPM cannot well describe the progressive failure process of landslide,except the residual stress state; whilst it is possible for the JCM to describe the mechanical behaviors of the whole process of the progressive failure of landslide body.It is shown that the main slip direction is only dependent on the failure body of landslide(simpli f ed as collapse body),the strike and the dip are the same as the collapse body.The rake angle is taken as the direction of vector sum of sliding force or of displacementof collapse body,i.e.the main slip direction is variable with deformation development.

2.Deformation mechanism,failure modes and control standards

2.1.Thrust-type landslide

The equations for deformation and force equilibrium of landslide body are established based on the fundamental mechanical behaviors of geo-materials.For the thrust-type landslide,it is assumed that the posterior region is under the post-failure stress state,and the front region is situated at the pre-peak stress state. The critical stress state is located in the region between the postfailure stress state and the pre-peak stress state,meaning a point (2D case)or a curve(3D case),when the sliding force is equal to the sliding resistance along the sliding surface direction.Two points,PresidandPc,are situated at the post-failure stress state,one pointPpeak(for 2D case)is at the critical stress state,and other points,Pb,PyieldandPa,are at the pre-peak stress state(see Fig.1a and d).The mechanical behaviors of these points are associated with different stress states(the post-failure stress state,the pre-peak stress state, and the peak stress state)of the whole load-displacement curve (see Fig.1d).The relationship between displacement of monitoring points on the sliding surface and time is shown in Fig.1a and b.A steady curve is presented for the pointsPyieldandPabecause their stress state is within the yield limit stress space,but an unsteady curve is observed for the pointsPresid,Pc,PpeakandPb,which are located in the post-failure stress state and the space between the yield limit stress and the peak stress.It can be noted that the mechanical properties of soft interlayer(sliding surface)are very important for controlling the stability of landslide(see Fig.1d).

The displacement-time curve can be roughly de f ned as the“S-shaped curve”for slope,which can be also divided into stable (types I and III)and unstable curves(type II)as shown in Fig.2.The displacement-height curve of sliding surface is a parabolic one atdifferent times(see Fig.1c).In addition,it can be deduced by theTScurve as plotted in Fig.2.

Two failure modes are proposed for the thrust-type landslide.In type I,failure occurs along the entire soft interlayer;in type II, failure takes place in the posterior region of landslide along the weak(sliding)face,but the shear failure may be produced in the front region of sliding mass,or inside the sliding mass.In this case, slope failure of heaving or in other forms can be observed.Two modes are controlled by the mechanical behaviors(shear stress and strain)of soft interlayer and sliding body,respectively.

Fig.2.Load-displacement curves of rock-soil mass and displacement-time curves of points on the sliding surface.

2.2.Pull-type landslide

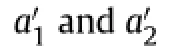
Fig.3.Relationship among deformation,time and height of sliding mass-mechanical behaviors of rock-soil mass of the pull-type landslide.

2.3.Relationship between displacement and time

The displacement-time curves and shear stress-strain(or load-displacement)curves of monitoring point on sliding surface are plotted in Fig.2.When the loads of rock-soil mass on the sliding surface are less than the yield limit loads(Tyield),the displacement-time curve is of the type I(stable curve).If the loads of rock-soil mass on the sliding surface range between the yield limit load(Tyield)and the peak load(Tpeak)or in the state of the post-failure,the displacement-time curve is of the type I(unstable curve).When the mechanical behaviors of geo-materials on the sliding surface show characteristics of type III,the displacementtime curve also shows the mode III(stable curve)features(see Fig.2).In other words,the displacement-time curve has two kinds of features,i.e.stable and unstable.

Fig.4.Schematic description of failure mode for pull-type landslide.Mode I:failure along sliding surface.Mode II:failure along sliding surface and sliding body.Mode III: tension failure of sliding body.

Fig.5.Distribution of stresses on sliding surface element.

3.Joint constitutive model(JCM)

Based on the above analyses of the deformation mechanism, failure modes and control standards of slope,a JCM,which can describe the mechanical behavior of geo-material with softening properties,is proposed.The constitutive relation of this JCM is proposed as

whereτandγare the shear stress(MPa)and shear strain,respectively;Gis the shear modulus(MPa);S,mandρare the dimensionless constants,-1＜ρ≤0 and 1+mρ≠0.

The critical strain space satis f es the following relation:

whereγpeakis the peak shear strain corresponding to the peak stress.

The critical shear stressτpeakis presented by the Mohr-Coulomb criterion:

wherecis the cohesion,σnis the normal stress,andφis the internal friction angle.

The peak shear strain(γpeak)is assumed to be only related to the normal stress and can be described as follows:

wherea1,a2,a3andξNare constant coef f cients.The unit ofa1anda2is in MPa;a3andξNare dimensionless coef f cients.

The parameterρcan be expressed as

whereρ0is the value whenσn=0;ρcis the value whenσn=σnc,σncis the experimental normal stress;andςis a constant coef f cient.

Eq.(5)can be obtained from the total shear stress-strain curves under different normal pressures.The above shear constitutive model can describe the total shear stress-strain characteristics and the mechanical behaviors of geo-materials of mode III(see Figs.1 and 2).The tensile failure of a sliding body can be presented by the traditional linear constitutive model.

4.Calculating methods of stability factor

4.1.Defnition of the main sliding direction

The process and mechanism of progressive failure of landslide have been described in previous studies.However,the de f nition of the main slip direction remains unclear.In this paper,the main slip direction of landslide is proposed.The collapse body of landslide is only involved with the main slip direction;the strike and the dip are the same as the collapse body;and the rake angle is taken as the direction of vector sum of sliding force or of displacement of collapse body.The main sliding direction varies with deformation development.

4.2.Comprehensive sliding resistance method(CSRM)

The stress f elds of the landslide body along the sliding surface (see Fig.6,where the dash lineABDECpresents the sliding surface) can be obtained by the current calculating method,and the vector sums of sliding force can be achieved in the directions ofx-,y-andz-axis,respectively:

wherePxs,Pys,Pzsare the vector sums of sliding force in the direction ofx-,y-andz-axis,respectively;Ωis the area of the whole integration;Ωfis the failure region;andΩRis the undamaged region.

The vector sum(Ps)ofPxs,PysandPzsis written as

Fig.6.Distribution of failure body and its projections inx-,y-,z-direction.

whereTxT,TyTandTzTare the vector sums of stabilizing force in the directions ofx-,y-andz-axis under the possible failure mode, respectively.

The vector sum(TT)ofTxT,TyTandTzTcan be written as

The direction cosine ofTTwith Cartesian coordinate axis is(αT, βT,γT).The vector angle(φc)betweenPsandTTcan be described by (see Fig.7):

The stability factors in thex-,y-,andz-direction are de f ned as

Fig.7.Relationship between the sums of sliding forces and sliding resistance under the possible failure mode.

The stability factor in the sliding force direction can be de f ned as

4.3.Main thrust method(MTM)

The MTM is only used to evaluate the stability of the thrust-type landslide.The critical state curve(see Fig.6,the dash lineDE)can be obtained.The residual pushing force from the posterior region to the critical state curve(DE)can be calculated(see Fig.6):

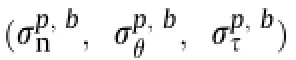
The vector sum(Tp)ofTxp,TypandTzpcan be written as

The direction cosine ofTpwith Cartesian coordinate axis is (αr,βr,γr).The vector angle(φm)betweenPpandTpcan be described as

The surplus stability factors in thex-,y-andz-direction can be respectively de f ned as

The surplus stability factor in the main slip direction is de f ned as

4.4.Main pull method(MPM)

The MPM is used to evaluate the stability of the pull-type landslide.The calculation of stability factor for modes I and II is similar to that of the thrust-type landslide.If the possible failure (mode III)is adopted,the tension failure of sliding body may occur, thus the MPM must be used to evaluate the tensile strength(σs,t)of the landslide body at a section.The tensile strength should be evaluated for each section of sliding body.The stability factors in thex-,y-,z-direction are respectively de f ned in the following forms:

The stability factor in the main tension direction is de f ned as

whereσs,tis the tensile stress of sliding body at a section under the present situation,andσc,tis the maximum tensile stress of landslide body at a section under possible failure mode.

4.5.Comprehension displacement method(CDM)

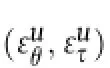
whereSxd,Syd,andSzdare the vector sums of displacement inx-,yandz-direction,respectively.The vector sum(Sd)ofSxd,Syd,andSzdis

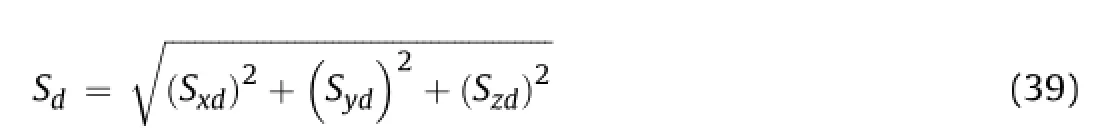
whereSxd,Syd,Szdare the vector sums of the displacement in thex-,y-andz-direction under the possible failure mode,respectively. The vector sum(Sd)ofSxd,SydandSzdis

The direction cosine ofSdwith Cartesian coordinate axis is(αd, βd,γd).The vector angle(φd)between the vectorSdandSdcan be calculated as

The stability factors in thex-,y-andz-direction are respectively de f ned as

The stability factor in the slip displacement direction is de f ned as

4.6.Surplus displacement method(SDM)

whereSxs,SysandSzsare the vector sums of displacement difference value in thex-,y-andz-direction between the possible failure mode and present status,respectively.The vector sum(Ss)ofSxs,SysandSzsis The direction cosine ofSswith Cartesian coordinate axis is(αs,βs, γs).The vector angle(φs)between vectorsSsandSscan be calculated by

The stability factors in thex-,y-,andz-direction are respectively de f ned as

The stability factor in the main slip direction is de f ned as

If the possible failure mode III is adopted for the pull-type landslide,the tension failure of landslide body may occur.The evaluation of tensile strain(3s,t)of the sliding body should then be performed.Each section of sliding body is evaluated by tensile strain,and the stability factors in thex-,y-,z-direction are respectively de f ned in the following forms:

The stability factor in the main tension direction is de f ned as

where3c,tis the maximum tensile strain of sliding body at a section under possible failure mode.

5.Sliding surface boundary method(SFBM)

The f nite element analysis based on SRM is often used to evaluate the stability of slope.It is,however,rather dif f cult to obtain a real result of stability factor,and the convergence of numerical calculation cannot be controlled.Five cases to produce nonconvergence can be observed in the literature(Lu et al.,2007,2008, 2012,2013,2014).On the other hand,the stability factor resulting from the f nite element analysis based on SRM cannot make a comparison with the current soil slice block method for the slope. In this section,the SFBM of FEM for the 2D landslide analysis will be discussed in detail.

5.1.SFBM of critical stress state

5.1.1.Implementation steps

Step 1:Select the sliding body as the f nite element calculation object(see Fig.8).In addition to the sliding surface’s force and displacement boundary condition,the other boundary conditions are consistent with the traditional calculating method.The representative element of sliding surface is adopted by beam or joint element.

Step 2:Use the PEPM to describe the mechanical behaviors of sliding surface,as is presented by

The boundary conditions of the normal stress,shear stress, normal strain,and shear strain of the sliding surface are given in the f rst step:

Fig.8.Layout of boundary element number of landslide.

Assuming that the absolute value of the tangential stress from the f rst to thek-th element is greater than the critical frictional stress,the force boundary condition of tangential stress is applied in the following form(see Fig.8):

When the absolute value of the tangential stress is smaller than the critical friction resistance,the force boundary conditions can be obtained by Eq.(66)(assuming that the elements are from the (k+1)-th to theN-th element).

Step 3:Perform the second calculation.The initial stress and strain boundary conditions of 1-kand(k+1)-Nelements are written as

According to Eqs.(70)and(71),the normal stress and tangential stress matrix of sliding surface element of the second calculation is obtained:

First,the comparisons between the calculated sliding stress and the critical friction stress corresponding to the normal stress of Eq. (72)are made.Then the critical friction stress in association with the normal stress of Eq.(72)is obtained by

The differences between the normal stresses of the upper face for thei-th calculation and lower surface of the sliding surface elements for the(i-1)-th calculation are compared.When the differential absolute value is greater than an assigned value(D1),the force boundary condition of sliding surface element is re-assigned by

The critical friction stress is applied by the sliding surface of the non-assigned value if its tangential stress is greater than the critical friction resistance:

Other elements are applied for the friction stress(expressed by Eq.(66)).The boundary stress and strain conditions for the third calculation matrices are presented as follows:

Step 4:Repeat the Step 3.In this case,the comparisons between the normal stresses are made again.When the absolute difference value is smaller than the assigned value(D1),the calculation is ended:

whereMMis the number of the calculations.

5.1.2.Critical state element and calculation of stability factor

The critical state element is de f ned in such a way that the sliding force is equal to the friction force along the sliding surface direction for an element.However,the absolute equality between the values of sliding force and friction force does not exist for the calculation of FEM.When the absolute difference between the sliding stress and the sliding resistance is smaller than an assigned value(D2),the element can be accepted as an critical state element, or the element will be separated into two elements,and the calculation can be performed until the condition,in which the absolute difference between the sliding stress and the sliding resistance is smaller than the assigned value(D2),is achieved.Thus the critical state element is obtained,i.e.the element“m”will be taken as a critical state element(see Fig.8).

The critical friction stress,the sliding stress,the surplus sliding stress,and the surplus friction stress for 1 tomelements along the sliding surface direction can be obtained as follows:

(3)The surplus sliding stress is

(4)The surplus frictional stress is 0.

The relative shear strain and shear stress f elds can be also obtained,and different stability factors(see Section 4)can be calculated according to Eqs.(80)-(82).

5.1.3.Stability factor obtained by the traditional SRM

The stability factor calculated by SRM is introduced under the condition of SFBM for FEM.The stability factor obtained by FEM will be compared with that obtained by the traditional soil slice block method.The condition of comparison between FEM and soil slice block method is that the calculating processes of these methods must be uniform,and the processes of soil slice block method is that the friction force reduction is performed until the surplus force of the last soil slice block is equal to zero.Based on this condition, the steps of f nite element analysis by PEPM can be realized.The shear stress and strain matrices of sliding surface element of the SFBM are obtained by

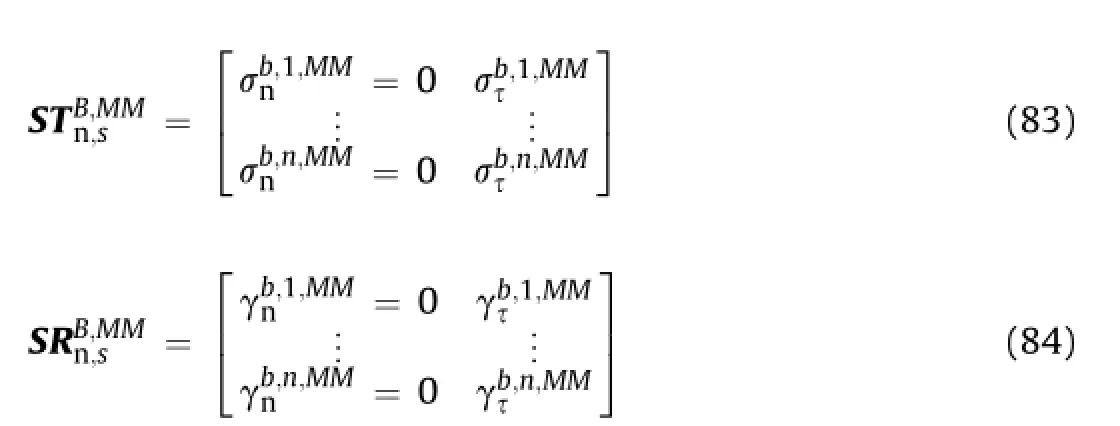
If the absolute value of sliding surface’s thrust stress of the f rst element is greater than the critical friction stress,the surplus sliding stress of the f rst element is expressed as

wheref1is the initial calculating stability factor.

The sliding surface boundary conditions of the f rst calculation by the SRM are written as

Fig.9.Mechanical behaviors of geo-materials by the new joint constitutive model(JCM).

The shear stress,normal stress,shear strain and normal strain of the upper sliding surface can be obtained.The sliding surface boundary conditions are obtained by the similar method introduced in Eqs.(88)and(89)for the second sliding surface element of the second calculation,which can be expressed as

5.2.Progressive failure analysis

The PEPM is only suitable for the residual stress state(or special loading condition),and the shear stress and strain f elds obtained by the PEPM are not compatible for other stress states.A new JCM is suitable for describing the progressive failure process of slope, which can be used to present the whole process characteristics of shear stress and shear strain of rock or soil mass.Specially,for the properties of softening behaviors,the real stress and strain f elds can be obtained by the JCM under the condition that the strength reduction coef f cient is equal to 1.Thus the stability of slope under different stress and deformation states can be predicted,i.e.the prediction of landslide failure is possible by considering the monitored deformation at different locations.

6.Case studies

A 2D slope is taken as an example in this context.The unit weightof sliding body is 20 kN/m3.The number of f nite elements is 564(see Fig.8).The model parameters are:

(1)The sliding surface:c=40 kPa,φ=15°,G=2.7 MPa, ρi,0=-0.99,ρi,c=-0.5,σnc，i=20 kPa,ςi=1.28,ai,1=53.0175 kPa,ai,2=56.1305 kPa,ai,3=0.01036,ξN,i=2.

(2)The landslide body:c=400 kPa,φ=28°,E=6.48 MPa,μ=0.2.

The JCM can describe the mechanical behaviors of geo-materials (see Fig.9),especially the softening properties.The stability factor of 1.1718 is obtained by the unbalance thrust method(soil slice block method),and the stability factors of 1.164 and 1.1203 are respectively calculated by PEPM and JCM under condition of the f nite element strength reduction.Different stability factors proposed in this paper are calculated by PEPM and JCM.The results are listed in Table 1.

7.Conclusions

In this paper,the deformation mechanism,failure mode,control standards and stability evaluation of thrust-type and pull-typelandslide are analyzed under 3D condition.Some results are drawn as follows:

Table 1Stability factors calculated by different models.

(1)The deformation and failure mechanisms of thrust-type and pull-type landslides are proposed,respectively,where the posterior(or front)region is located at the post-failure(or prepeak)stress state.The critical stress state exists between the post-failure and the pre-peak stress states for the two types of landslides.The related critical stress state element(or soil slice block)is suggested for the FEM(or soil slice block method),and the corresponding methods for determining the critical stress state are performed.

(2)Two failure modes are proposed for thrust-type landslides,and three failure modes for pull-type landslides.All the failure modes are controlled by the mechanical behaviors of relative shear stress and shear strain(or the traction stress and tensile strain of sliding body).The critical stress state point(or curve) gradually moves from the posterior(or front)to the front (posterior)region of landslide body.A new peak stress state and post-failure stress state will progress during landslide deformation and failure.

(3)A JCM is proposed to describe the mechanical behaviors of geomaterials.The mechanical properties of the modes I and III can be presented by the JCM,especially the softening behaviors of rock or soil mass.

(4)A comparison is made between the whole load-displacement and displacement-time curves proposed.The S-shaped curve is suggested to describe the relationship between the monitored displacement and time for the point on sliding surface during the progressive failure process of landslide.It is possible for the relation between the monitored displacement of sliding surface and height of landslide body to be presented by the parabolic curve,which can be used to predict the failure of landslide and is called“graphic method”.

(5)The stability factors obtained by traditional methods may have no physical meanings in a sense from the mechanical views.It can be merely called“empirical method”.The f ve stability factors(CSRM,MTM,CDM,MPM,and SDM)are suggested to describe the stability of progressive failure of landslide,and it is feasible for CSRM,MTM and MPM to evaluate the stability of slope.

(6)The main slip direction of landslide is de f ned,and the failure body of landslide(simpli f ed as collapse body)is only involved with the main slip direction.The strike and the dip of the landslide are the same as those of the collapse body,and the rake angle is taken as the direction of vector sum of sliding force or of displacement of collapse body,i.e.the direction of main sliding varies during the progressive failure process.

(7)The cause of non-convergence for the numerical analyses of

slope by FEM is discussed.A new model to consider the slip face as the boundary condition is suggested to evaluate the stability of slope.The boundary conditions of sliding surface can be described not only by the PEPM,but also by the JCM.The results obtained by the PEPM are compared with those of traditional slice block method.It can be noted that the PEPM is not suitable for describing the progressive failure process,except the residual stress state of sliding surface.The real stress and strain f elds of slope can be obtained by the JCM,and the determination of sliding surface can also be achieved by the JCM for slope stability analysis.

Con f ict of interest

The authors wish to con f rm that there are no known con f icts of interest associated with this publication and there has been no signi f cant f nancial support for this work that could have in f uenced its outcome.

Acknowledgments

The supports from the National Natural Science Foundation of China(Grant No.41372363)and National Important Research of China(Grant No.E0907-90815018)are acknowledged.

Guo MW,Ge XR,Wang SL.Slope stability analysis under seismic load by vector sum analysis method.Journal of Rock Mechanics and Geotechnical Engineering 2011;3(3):282-8.

Li N,Qian QH.Four criteria of stability analysis and assessment of high rock slope. Chinese Journal of Rock Mechanics and Engineering 2010;29(9):1754-9(in Chinese).

Liu GR,Yan EC,Lian C.Discussion on classi f cation of landslides.Journal of Engineering Geology 2002;10(4):339-42(in Chinese).

Liu YZ,Ge XR,Li CG,Wang SL.Stability analysis of slope and dam foundation based on vector method safety factor.Chinese Journal of Rock Mechanics and Engineering 2007;26(10):2130-40(in Chinese).

Lu KL,Zhu DY,Xu Q,Yang Y.3D back analysis of shear strength parameters of slip soil.Rock and Soil Mechanics 2010;31(10):3319-23(in Chinese).

Lu YF,Deng GD,Yang LP,Liu DF.Study of mechanical behaviors of key block and characteristics of force transmit and stability coef f cient of different stress states of landslides.Chinese Journal of Rock Mechanics and Engineering 2014;33(5): 884-91(in Chinese).

Lu YF,Lu T,Zhou JJ,Wu XX.A new constitutive model and its application to pile foundation analysis.Rock and Soil Mechanics 2012;34(4):967-73(in Chinese). Lu YF,Wu YC,Yang LP,Cui YJ.Investigation on determination of thermo-dynamical parameters of unsaturated soil.Rock and Soil Mechanics 2008;29(7):1747-52 (in Chinese).

Lu YF,Yang LP,Liu DF.A new joint constitutive model and several new methods of stability coef f cient calculation of landslides.Chinese Journal of Rock Mechanics and Engineering 2013;32(12):2431-8(in Chinese).

Lu YF,Zhou SP,Luo XQ,Wu YC.Evaluation of effects of seepage on landslide reinforced by anti-sliding piles.Chinese Journal of Rock Mechanics and Engineering 2007;26(9):1840-6(in Chinese).

Wang JF.Theoretical analysis to two classic landslide prediction models:Saito’s model and Voight’s model.Journal of Geomechanics 2004;10(1):40-50(in Chinese).

Yao HL,Zheng SH,Chen SY.Analysis on the slope stability of expansive soils considering cracks and in f ltration of rain.Chinese Journal of Geotechnical Engineering 2001;23(5):606-9(in Chinese).

Yin KL,Wang Y,Tang ZH.Mechanism and dynamic simulation of landslide by precipitation.Geological Science and Technology Information 2002;21(1):75-8 (in Chinese).

Zhang Z,Li SH,Ma L.Probability analysis of relationship between landslide and rainfall in Chongqing area.Chinese Journal of Rock Mechanics and Engineering 2005;24(17):3185-91(in Chinese).

Zheng H,Yang ZL,Sun GH.Extremum solutions to the limit equilibrium method subjected to physical admissibility.Natural Hazards 2013;65(1):79-96.

Zheng H.A rigorous three-dimensional limit equilibrium method.Chinese Journal of Rock Mechanics and Engineering 2007;26(8):1529-37(in Chinese).

Zheng XY.Summary on the methods of prediction to landslide.World Geology 2000;19(4):370-4(in Chinese).

Zhu DY,Qian QH.Rigorous and quasi-rigorous limit equilibrium solutions of 3D slope stability and application to engineering.Chinese Journal of Rock Mechanics and Engineering 2007;26(8):1513-28(in Chinese).

Dr.Yingfa Luis working as a professor in the School of Civil Engineering and Architecture,Hubei University of Technology,Wuhan,China.His research interests mainly cover rock and soil mechanics,geo-technical engineering, slope stability,natural disaster monitoring and prediction, foundation engineering,etc.He has proposed a new theoretical system of progressive deformation and failure mechanism and f ve new calculating methods of stability factor of slope,and it is also proved that the perfect elasto-plastic model is not suitable for describing the progressive failure process of slope,and that the yield limit stress space is changed with the damage evaluation,that is,the initial proportional yield limit stress is decreased with the damage development for most geo-materials.A generalized constitutive model is suggested to describe the complete process properties of stress(or load)and strain(or displacement)of rock-soil mass for the f rst time. Till now he has published more than 80 research papers in different journals related to this subject.

*Tel.:+86 13807127673.

E-mail address:lyf77@126.com.

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2015.02.008