形如Δ2u=f1(x)f2(y)的泊松方程齐次化判定方法

马春兰，臧涛成，葛丽娟

（苏州科技学院数理学院，江苏苏州215009）

形如Δ2u=f1(x)f2(y)的泊松方程齐次化判定方法

马春兰，臧涛成，葛丽娟

（苏州科技学院数理学院，江苏苏州215009）

讨论了形如Δ2u=f1(x)f2(y)的泊松方程齐次化问题，给出了判定该类型泊松方程是否能够进行齐次化的判别式以及求解其特解的方程。

泊松方程；非齐次项；定解问题；特解

泊松方程Δ2u=f在静电场电势、稳定温度分布等许多数学物理及工程技术领域中都会涉及。理论上该方程可采用格林函数积分法进行求解[1-2]，但该法积分运算比较复杂，一般难以得到直接的解析解。另一种解法为齐次化方法[1-8]，即将原关于u的泊松方程通过某种方式（如找特解）转化为可采用分离变量法求解的拉普拉斯方程，采用的方法基本是罗列方程非齐次项f呈现何种特殊形态时方程可齐次化。那么，对泊松方程是否存在一个统一的判定方法呢？笔者针对这一问题，对形如Δ2u=f1(x)f2(y)的泊松方程进行了分析，得到了判定该类型泊松方程是否能够进行齐次化的判别方法及求解其特解的方程。

1 Δ2u=f1(x)f2(y)齐次化判定条件及特解满足的方程

不失一般性，考虑如下直角坐标下的泊松方程第一边值问题（定解条件全为非齐次时可用叠加原理化为包括下述（1）在内的两个定解问题，另一个则可用熟悉的分离变量法求解）

如何才能够判定定解问题（1）中方程能够齐次化（当然方程齐次化后的定解问题也要有一组边界条件保持齐次）呢？或者说，非齐次项必须满足什么条件才能保证（1）可以齐次化？

为此，令

其中g(y)≠0是待求函数。通过（2）式，将原关于u(x,y)的泊松方程定解问题转化为关于v(x,y)的拉普拉斯方程定解问题。v(x,y)显然应满足

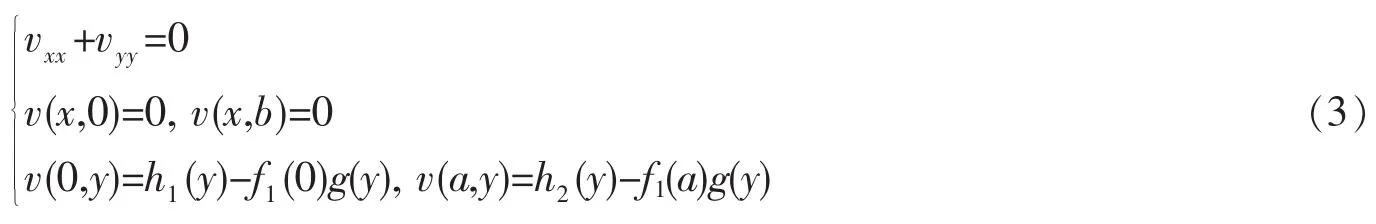
为寻求f1(x)满足何种条件才能找到待求函数g(y)，将（2）代入（1）有

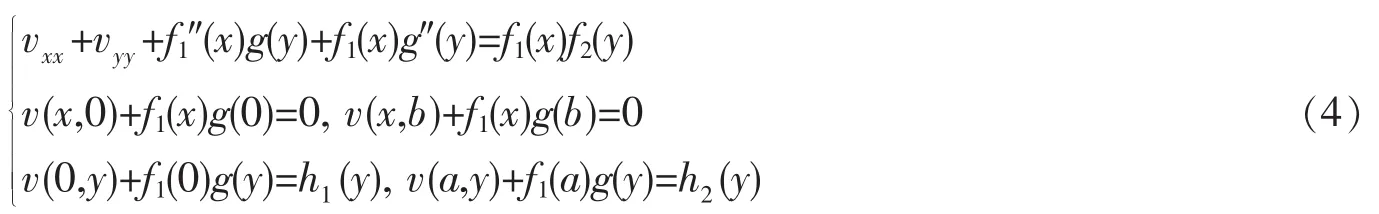
考虑到（3），显然应有

由（5）之第一式可得

因g(y)≠0，所以

左边为x的函数与y无关，右边为y的函数与x无关，（6）式成立的条件是等式两边同时等于一常数k，即

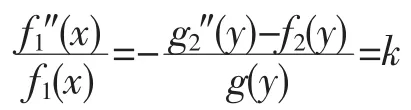
由此可知，当f1(x)满足

时，也即f1(x)为线性函数（k=0）、e的指数函数（k＞0）（或双曲函数）或正余弦三角函数（k＜0）时，待求函数g(y)存在，定解问题（1）能够进行齐次化。

此时，待求函数g(y)满足的方程为

由上式和（5）之第二式可得完全确定g(y)的如下表达式

至此，对定解问题（1），只要f1(x)满足（7）式，就可通过（8）式求得g(y)，从而得到齐次化函数f1(x)g(y)，进而通过（3）式和（2）式最终求得（1）式的解。

2 推论

（1）对于其他边界条件情形（如第二类或混合边界条件），根据（4）知（8）式仍然适用；

（2）以上结论可适用于满足（7）式的各种函数的若干加减组合（见例题2）；

（3）对于形如

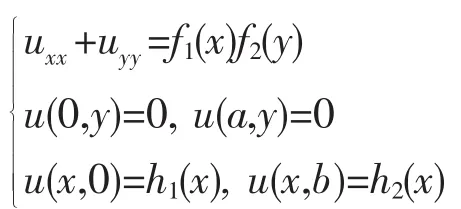
的定解问题，只要f2(y)满足（7），那么齐次化函数f2(y)g(x)中的g(x)完全类似于（8）

3 实例

例1求定解问题[2]。

解f1(x)=x，f2(y)=-2A，满足判定式（7）f1″(x)=kf1(x)且k=0，定解问题的方程和边界条件可同时齐次化。由（8）得

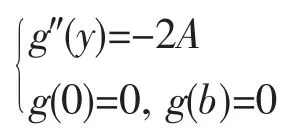
解得

代入（2）式中有

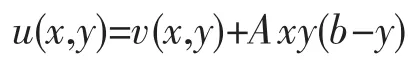
再由（3）式得

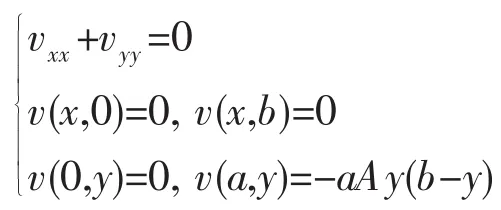
采用分离变量法求得解为

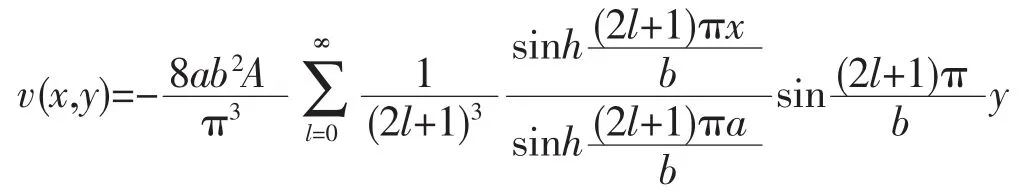
最后

此题在文献[2]中是用猜的方法得到能同时使得变换后v(x,y)的方程及y方向边界条件同时为齐次的特解Axy(b-y)，这在非齐次项相对简单（如例1）时还可能做到，但对复杂一些的情况（如例2）就不那么容易用猜的办法了。

例2对定解问题

设u=v+w，试求特解w，使得变换后关于v的方程和一组边界条件为齐次。

解将定解问题化为（1）的形式。为此令，并设及ui的特解为wi，这样

i=1时：可令f11(x)=a，f21(y)=1，故有k=0，由（8）

得

特解为

i=2时：f12(x)=sinx，f22(y)=y，因y″=0·y和(sinx)″=-sinx，故可取k=0或k=-1，考虑到i=1时在y方向边界条件为齐次，所以取k=-1。这样，由（8）

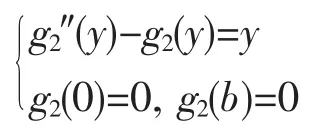
得

特解为

i=3时：f13(x)=ex，f23(y)=y2，因（ex）″=ex，故k=1，由（8）

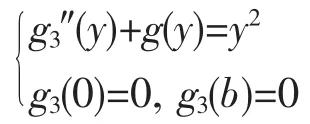
得

特解为

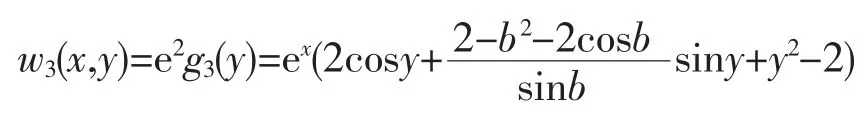
这样

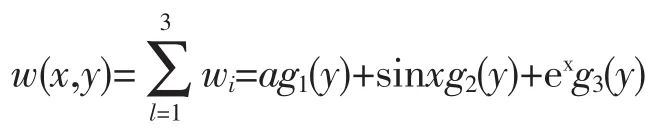
因为

所以w(x,y)就是所要求的原问题的特解。

[1]梁昆淼.数学物理方法[M].3版.北京：高等教育出版社，1998：148-150，220.

[2]周治宁.数学物理方法习题指导[M].北京：北京大学出版社，2004：212-213.

[3]臧涛成.具有特殊非齐次项泊松方程的特解法[J].大学数学，2011，27（2）：138-141.

[4]臧涛成.具有特殊非齐次项波动方程的处理方法[J].大学物理，2009，28（3）：10-12.

[5]石文善.线性偏微分方程非齐次定解问题的待定函数法[J].大学物理，1992，28（3）：10-12.

[6]杨燕.关于泊松方程的解[J].文山高等师范专科学校学报，2002，14（1）：65-68.

[7]李其深.一种求泊松方程特解的方法[J].工科数学，1994（2）：110-114.

[8]夏志.泊松（Poisson）方程特解的待定函数解法[J].辽宁工学院学报，2006，26（1）：66-69.

The homogeneous method of Poisson equation such as Δ2u=f1（x）f2（y）

MA Chunlan，ZANG Taocheng，GE Lijuan
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

The transformation of nonhomogeneous Poisson equations such as Δ2u=f1(x)f2(y)into homogeneous equations is discussed.We proposed a criterion for this kind of Poisson equations being able to be homogenized. And the equation for the special solution was given.

Poisson equation；nonhomogeneity；definite problem；particular solution

O411.1

A

1672－0687（2015）02－0033－04

责任编辑：李文杰

2014－12－17

国家自然科学基金资助项目（11304218）；校重点专业建设资助项目（2013zyxz-08）

马春兰（1973-），女，江苏盐城人，副教授，博士，研究方向：凝聚态物理等。