具有第二下降点8错线性复杂度的2n周期序列
王喜凤,周晓明,周建钦
(安徽工业大学计算机科学与技术学院,安徽马鞍山243002)
具有第二下降点8错线性复杂度的2n周期序列
王喜凤,周晓明,周建钦
(安徽工业大学计算机科学与技术学院,安徽马鞍山243002)
基于构造方法和方体理论,研究以2错线性复杂度为第一下降点并以8错线性复杂度为第二下降点的周期为2n的二元序列,分析第一下降点与第二下降点的关系;并给出所有可能的8错线性复杂度的取值形式,同时推导出以2错线性复杂度为第一下降点并以8错线性复杂度为第二下降点的2n周期二元序列的完整的计数公式。使用文中方法,同样也可给出其他以k错线性复杂度第二下降点或第三下降点的二元序列相关性质。
周期序列;线性复杂度;k错线性复杂度;方体理论
作为衡量密钥流序列强度的一个重要指标,周期序列的线性复杂度在研究流密码的安全性方面有很重要的意义。将能够产生序列s的最短的LFSR(线性反馈移位寄存器)的级数定义为s的线性复杂度,记为L(s),可由Games-Chan算法[1]计算。
线性复杂度高的序列并不一定保证序列是安全的,有些序列的线性复杂度极不稳定,若改变其一个周期中的若干个元素,会使这些序列的线性复杂度发生很大的变化,此种序列仍然属于密码学上的弱序列。我国学者丁-肖-单[2]最先注意到这个问题,因而提出了流密码的稳定性理论,并提出了重量复杂度、球体复杂度等流密码稳定性度量指标。国外学者Stamp和Martin[3]随后引入了类似“球体复杂度”的错线性复杂度Lk(s):设序列s是周期为N的q元序列,当改变s一个周期中至多k(0≤k≤N)位,得到所有序列的线性复杂度中的最小值,可由B-M算法[4]及其改进算法计算,并引入了k错线性复杂度曲线的概念。
关于k错线性复杂度下降点,Etzion[5]提出了关键错误线性复杂度分布CELCS(critical error linear complexity spectrum)。CELCS由一系列关键错误点(k,Lk(s))构成,满足Lk(s)>Lh(s),k<h,序列线性复杂度的下降只发生在这些关键错误点处。对第一次下降点已有许多学者进行了研究,如文献[6-7]。
文中研究以2错线性复杂度为第一下降点并以8错线性复杂度为第二下降点的周期为2n的二元序列,分析第一下降点与第二下降点的关系,并给出了8错线性复杂度所有可能的取值,推出满足已知2错和8错线性复杂度的序列计数公式,并通过计算机编程进行验证。
1 预备知识与引理
设有限域GF(2)上的两个向量X=(x1,x2,…,xn)和Y=(y1,y1,…,yn),则定义X+Y=(x1+y1,x2+y1,…,xn+yn)。文中所涉及的序列均为有限域GF(2)上的序列,其中的运算都是模2运算。
设sN为序列s的一个周期,当N=2n时,sN可记为s(n),以下讨论的都是周期为2n的二元序列。周期为N的序列s的Hamming重量定义为在s的每个周期中非零元素的个数,记为WH(s)。序列中两元素间距离指的是两个元素的下标之差,如周期为N序列,则元素si,sj的距离为(j-i),其中0≤i<j≤N。
引理1设周期为N=2n的二元序列s(n),其线性复杂度L(s(n))=2n,当且仅当该序列一个周期中的Hamming重量为奇数。
引理2[8]设N(L)为线性复杂度为L的周期为2n的二元序列的个数,则当L=0时,N(L)=1;当1≤L≤2n时,N(L)=2L-1。
引理3已知序列s1(n)和s2(n)是周期为2n的二元序列,若L(s1(n))≠L(s2(n)),则有L(s1(n)+s2(n))= max{ L(s1(n)),L(s2(n))};若L(s1(n))=L(s2(n)),则有L(s1(n)+s2(n))<L(s1(n))。
设s是一个序列,s的k错线性复杂度为c,e为Hamming重量为k的误差序列,可假设s=t+e,L(t)=c。文中研究周期为2n的二元序列s的k错线性复杂度的若干性质,为此引入重要框架:设集合S={t|L(t)=}c,E={e|WH(e)=k},SE={t+e|t∈S,e∈E},其中t是线性复杂度为c的序列,最终从序列SE中筛选满足Lk(t+e)=c的序列t+e。
对于给定的线性复杂度c,在求满足Lk(t+e)=c的序列t+e的过程中需排除两类序列:第一类序列是t+ u∈SE,但Lk(t+u)<c;第二类序列是x+u,y+v∈SE,Lk(x+u)=Lk(y+v)=c,且x=y,u=v,但x+u=y+v,其中x,y∈S,u,v∈E。
对于Lk(t+u)<c的情况,相当于存在序列v,使Lk(t+u)=Lk(t+u+v)<c。因为L(t)=c,由引理3知,L(u+v)= c,等价于检查是否存在序列v,使L(u+v)=c。
对于Lk(x+u)=Lk(y+v)=c,且x+u=y+v的情况。因x+u=y+v,则x+y=u+v;又因L(x)=L(y)=c,由引理3可知,L(x+y)<c,则L(u+v)<c,等价于检查是否存在序列v,使L(u+v)<c,其中WH(u)=WH(v)=k。若存在这样的序列v,则统计v的个数。
2 具有第二下降点8错线性复杂度的2n周期二元序列计数
该节中,首先介绍方体理论[9]的相关知识。接着研究序列k错线性复杂度的第一下降点与第二下降点的关系,给出k错线性复杂度的所有可能取值形式,并推出以2错线性复杂度为第一下降点并以8错线性复杂度为第二下降点的周期为2n的二元序列s(n)的计数公式。
定义1设序列s中两个非零元素的位置之差为(2x+1)2y,其中x和y均为整数,则称这两个元素的距离为2y;若这两个元素组成一条边,则称边长为2y;若这两个元素组成一条棱,则称棱长为2y。
定义2设周期为2n的二元序列s中有2m个非零元素,0≤i1<i2<…<im<n。若m=1,则s中有2个非零元素,且距离为2i1,称为1方体。若m=2,则s中有4个非零元素组成一个矩形,边长分别为2i1和2i2,称为2方体。一般情况,s中有2m-1个非零元素组成(m-1)方体,余下2m-1个非零元素也组成(m-1)方体,且2m-1对元素之间的距离均为2im,则称序列s称为m方体,且称序列s的线性复杂度为方体的线性复杂度。
定理1设序列s是周期为2n的二元序列,序列中非零元素组成一个m方体,棱长分别为2i1,2i2,…,2im,0≤i1<i2<…<im<n,则线性复杂度L(s)=2n-(2i1+2i2+…+2im)。
定理2已知周期为2n的二元序列s(n),且L(s(n))<2n。
(1)L8(s(n))<L7(s(n))=L6(s(n))=…=L2(s(n))<L1(s(n))=L(s(n)),当且仅当s(n)可分解为若干方体c1,c2,c3,…,cn,L(c1)>L(c2)>L(c3)…>L(cn),其中c1为1方体,c2为3方体,且c1和c2的非零元素均不相交,或有一个重合;(2)L8(s(n))<L7(s(n))=L6(s(n))=…=L2(s(n))<L1(s(n))=L(s(n)),当且仅当L2(s(n))=2n-(2j1+2j2+2j3),0≤j1<j2<j3<n,且L2(s(n))≠2n-(1+2+22)。
证明(1)①必要性:当1方体c1和3方体c2中的非零元素互不相交时,去掉c1中的所有非零元素,或当c1和c2中有一个非零元素重合时,在重合位置为c2的补一个非零元素,此时,c2是s(n)的2错线性复杂度序列的最大方体。由Kurosawa[6]知,对周期为2n的二元序列s(n)的Lk(s(n))严格小于L(s(n))=2n-(2i1+2i2+…+ 2im)的k的最小值kmin=2m。又因c2是3方体,则L2(s(n))=L4(s(n))=L6(s(n))。当c1和c2的非零元素互不相交时,在c1上增加6个非零元素,使c1变为与c2同类型的3方体,则c1,c2可构成一个4方体。因此,s(n)的8错线性复杂度序列最大的方体为4方体,线性复杂度下降,即L8(s(n))<L2(s(n))。当c1与c2中的非零元素有一个重合时,将c1+c2中8个非零元素均变为零素,此时c3是s(n)的8错线性复杂度序列中的最大方体,则L8(s(n))<L2(s(n)),线性复杂度同样会下降。
②充分性:假设c1,c2与c3均是1方体,其中非零元素互不相交,且在c1,c2,c3中增加2个元素,不能构成3方体。当c1与c2的非零元素互不相交时,将c1和c2的非零元素变为零,线性复杂度下降,L4(s(n))<L2(s(n))与L2(s(n))=L4(s(n))矛盾,则此情况不存在。
假设c1是1方体,c2是2方体,c1与c2的非零元素既可以不相交,也可有一个重合。当c1与c2的非零元素不相交时,去掉c1和c2的非零元素,则线性复杂度下降,即L6(s(n))<L2(s(n)),与已知条件矛盾。当c1和c2有一个非零元素重合时,去掉c1+c2中的非零元素,则线性复杂度下降,即L4(s(n))<L2(s(n)),与已知条件矛盾。
假设c1是1方体,c2是4方体,c1与c2的非零元素既可以不相交,也可以有一个重合。因c2是4方体,需改变至少16个元素线性复杂度才可能会下降,与L8(s(n))<L2(s(n))矛盾。
综上所述,只有c1为1方体,且c2为3方体的情况满足已知条件。
(2)由(1)易知,L8(s(n))<L2(s(n))<L(s(n)),当且仅当L2(s(n))=2n-(2j1+2j2+2j3),其中0≤j1<j2<j3<n。接着证明L2(s(n))≠2n-(1+2+22),因c1为1方体,c2为3方体,若L(c2)=2n-(1+2+22),则L(c1)=2n-1或2n-2或2n-22,则方体c1,c2中各存在1个非零元素,使得这两个元素间的距离d>22。假设L2(s(n))=2n-(2j1+2j2+2j3),则2j3≥d> 22,可得L2(s(n))≠2n-(1+2+22)。
下面研究以2错线性复杂度为第一下降点并以8错线性复杂度第二下降点的周期为2n的二元序列的L8(s(n))的所有可能取值情况。
定理3设序列s(n)为周期为2n的二元序列,如果L8(s(n))<L2(s(n))<L(s(n)),且L(s(n))=2n-2i0,L2(s(n))=2n-(2j1+2j2+2j3),0≤j1<j2<j3<n,则
证明以下证明基于框架:SE={t+e|t∈S,e∈E},其中L(t)=L8(s(n)),WH(e)=8,L2(e)=2n-(2j1+2j2+2j3)。使用筛选法,从SE中筛选出L8(t+e)=L的序列t+e。
(1)当L8(s(n))=2n-(2i1+2i2+…+2im),m>4时,s(n)的8错线性复杂度序列中有2m个非零元素。关于Lk(t+u)<c的情况,等价于存在序列v,使得L(u+v)=c。因WH(u)=WH(v)=8,则序列u+v的最多有16个元素,小于2m,所以L(u+v)不可能等于L8(s(n)),即不存在序列v,使得L(u+v)=L8(s(n))。
(2)当L8(s(n))=2n-(2i1+2i2+2i3+2i4)时,
①用反证法证明L8(s(n))=2n-(2i1+2i2+2i3+2i4),其中{i1,i2,i3,i4}≠{j1,j2,j3,j4}。假设n=5,i0=1,j1=0,j2=2,j3=4,u(5)={1110 1100 0000 0000 0100 1100 0000 0000},则存在序列v(5)={0001 0011 0000 0000 1011 0011 0000 0000},使得u(5)+v(5)={1111 1111 0000 0000 1111 1111 0000 0000},则L(u(5+v(5))=2n-(2j1+2i0+2j2+2j3)=25-(1+ 2+4+16)<L=L8(s(n)),因此,L8(s(n))≠2n-(2i1+2i2+2i3+2i4),其中{i1,i2,i3,i4}={j1,i0,j2,j3}。
用型号为XRF-1800X的射线荧光光谱仪,对AE44雷达外壳本体试样进行元素定量分析;用型号为HB-3000B布氏硬度计,测试AE44雷达外壳的宏观硬度;用型号为CMT5105电子万能试验机,测试试样的拉伸性能;用型号为MR2000型金相显微镜,观察试样的显微组织;用型号为D/MAX2500V的X射线衍射仪,对试样的物相组成进行分析;用型号为JSM-6490LV扫描电子显微镜拍试样扫描照片,并且用与之匹配的INCA能谱仪对相应位置进行成分定性和定量分析.
②用反证法证明L8(s(n))=2n-(2i1+2i2+2i3+2i4),其中{i1,i2,i3,i4}≠{0,1,2,3},即L8(s(n))=25-(20+21+22+23)。
因为,L8(s(n))<2n-(2j1+2j2+2j3)<2n-2i0,则2i0<2j1+2j2+2j3<1+2+4+8。
假设L(t)=25-(20+21+22+23),对任意u∈E有L2(t+u)=2n-(2j1+2j2+2j3),易证L8(t+u)<2n-(20+21+22+23)。
(3)当L8(s(n))=2n-(2i1+2i2+2i3)时,下面使用反证法证明{j2,j3}{i1,i2,i3},即证{j2,j3,x}≠{i1,i2,i3},其中x为一正整数,0≤x<n,x≠j2,j3。
假设s5是周期为25的二元序列,且L(s(5))<25。若L(s(5))=2n-2i0=25-1,L2(s(5))=25-(2+22+23),则L8(s(5))≠2n-(2j2+2j3+2x)=25-(22+23+2x)。
设L8(s(5))=25-(22+23+2x),当x=0,1时,L8(s(n))>L2(s(n)),则x只能取4。根据框架SE={t+e|t∈S,e∈E},使S={t|L(t)=25-(2+23+24)},E={e|WH(e)=8},最后根据筛选法从集合SE中筛选出满足L8(t+e)=25-(2+23+24)的序列t+e。
现考虑s+u∈SE,L8(s+u)<25-(22+23+24)的情形,等价于检查是否存在序列v∈E,使得L(u+v)=25-(22+ 23+24)。
若已知序列u={1110 1010 0000 0000 0010 1010 0000 0000},则存在一个序列v={1100 1000 0010 0000 1000 0010 0010}∈E,使L(u+v)=25-(22+23+24),则L8(u+v)<25-(22+23+24)。又L2(t+v)=25-(2+22+23),则{i1,i2,i3}≠{j2,j3,x},即{j2,j3}{i1,i2,i3}。同理可得,{j1,j2}{i1,i2,i3},{j1,j3}{i1,i2,i3}。
定理4设s(n)为周期为2n的二元序列,且L(s(n))=2n-2i0
(1)若L8(s(n))<L2(s(n))<L(s(n)),其中L2(s(n))=2n-(2j1+2j2+2j3),0≤j1<j2<j3<n,
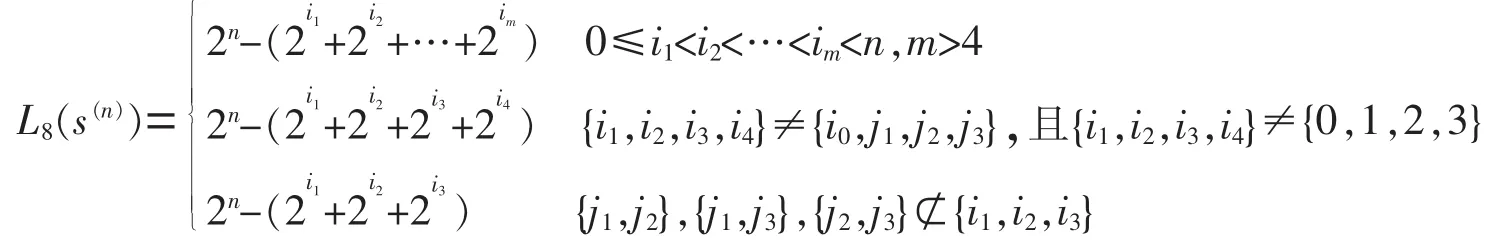
则满足以上条件的周期为2n的二元序列s(n)的个数为

其中,当L8(s(n))=2n-(2i1+2i2+2i3+2i4)时,im=i4;当L8(s(n))=2n-(2i1+2i2+2i3)时,im=i3;L=L8(s(n));,,。
(2)如果L8(s(n))=0,则N(s(n))=28n-3j3-2j2-j1-i0-11/γ。
证明令S={t|L(t)=L},E={e|WH(e)=8},SE={t+e|t∈S,e∈E},其中序列t的线性复杂度,序列e满足L2(e)=2n-(2j1+2j2+2j3)及WH(e)=8。最后,从集合SE中筛选出满足L8(t+e)=L的序列t+e。
(1)由引理2可知,线性复杂度L(t)=L的周期为2n的二元序列的个数2L-1。
(2)以下证明满足条件WH(e)=8和L2(e)=2n-(2j1+2j2+2j3)的序列e的个数为N(e)=28n-3j3-2j2-j1-i0-11/γ。
①假设s(j1)是周期为2j1的二元序列,若L(s(j1))=2j1,WH(s(j1))=1,则序列s(j1)的个数为N(s(j1))=2j1;
②若j2>j1,周期为的二元序列s(j2),L(s(j2))=2n-2j1=2j2-2j1,WH(s(j2))=2,因L(s(j2))-L(s(j1+1))=(2j2-2j1)-(2j1+1-2j1)=2j2-1+2j2-2+…+2j1+1有(j2-j1-1)项,则序列s(j2)的个数为N(s(j2))=(22)j2-j1-1×N(s(j1+1))=(22)j2-j1-1×2j1= 22j2-j1-2;
因此,满足L(s(j2+1))=2n-(2j1+2j2)=2j2+1-(2j1+2j2)=2j2-2j1,WH(s(j2+1))=4的周期为2j2+1的二元序列s(j2+1)的个数为N(s(j2+1))=N(s(j2))=22j2-j1-2;
③若j3>j2>j1,则周期为的二元序列s(j3),满足,又因多项式L(s(j3))-L(s(j2+1))=2j3-1+2j3-2+…+2j3+1共有(j3-j2-1)项,则序列s(j3)的个数为N(s(j3))=(24)j3-j2-1×N(s(j2+1))=(24)j3-j2-1×22j2-j1-2= 24j3-2j2-j1-6;
因此,满足L(s(j3+1))=2j3+1-(2j1+2j2+2j3)=2j3-2j2-2j1,WH(s(j3+1))=8的周期为2j3+1的二元序列s(j3+1)的个数为N(s(j3+1))=N(s(j3))=24j3-2j2-j1-6。
由上可知,满足e∈E,L2(e)=2n-(2j1+2j2+2j3)的序列e的个数为N(e)=24j3-2j2-j1-6,则满足u∈E,L2(u)=2n-(2j1+2j2+2j3)的序列u的个数为。
其中,当i0<j2时,γ=1;当i0>j2时,γ=2。
下面举例说明当i0>j2时,γ=2。假设n=4,i0=2,j1=0,j2=1,j3=3,u(4)={1111 1000 0111 0000},则移动u(4)中的非零元素得,使。
接着举例说明当i0>j2时,γ=1。假设n=4,i0=1,j1=0,j2=2,j3=3,u(4)={1110 1100 0100 1100},则由序列u(4)移动相应的非零元素仅能找到唯一的序列,v(4)={1100 1100 1100 1100},使L(v(4))=24-(20+21+23)。
(3)因s+u,t+v∈SE,L8(s+u)=L8(t+v)=L,其中s≠t,u≠v但s+u=t+v,检查是否存在序列v,WH(u)=WH(v)=8,使L(u+v)=L(s+t)<L,若存在,则统计满足条件的序列v的个数。
①情形一:对于i0
对于∀u∈E,存在1个序列v,使L(u+v)=2n-(2j1+2i0+2j2+2j3)<L,即δ=1;存在3个序列v,使L(u+v)=2n-(2j2+2i0+2j3)<L,即δ=2;存在7个序列v,使L(u+v)=2n-(2j1+2i0+2j3)<L,即δ=3;存在15个序列v,使L(u+v)= 2n-(2i0+2j3)<L,即δ=4。

②情形二:对于im<ω<n
对于im<ω<n,存在255×(28)ω-im-1个序列v,使2n-(2j2+2j3+2ω)<L,或2n-(2j1+2j3+2ω)<L,或2n-(2j3+2ω)<L,或2n-(2j2+2j2+2ω)<L,或2n-(2j2+2im+2ω)<L,或2n-(2j1+2ω)<L,或2n-(2i0+2ω)<L,或2n-2ω<L。
对任意有8个非零元素的序列v,周期翻倍且非零元素个数不变时,可得28个新序列。因此,存在255+ 255×28+…+255×(28)n-im-2=(28)n-im-1-1个序列v,使L(u+v)<L。
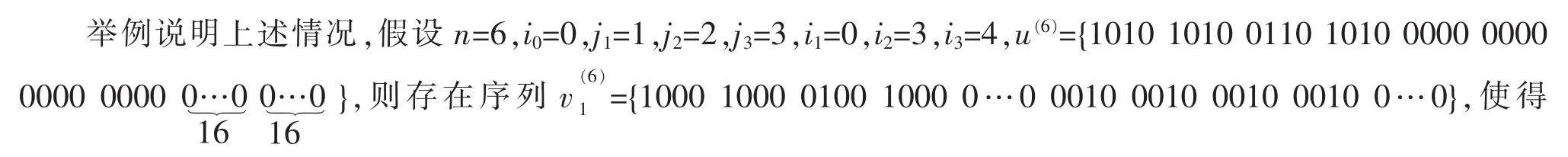

因此,存在(28)n-im-1-1=(28)n-i3-1-1=(28)6-4-1-1=255个序列v,使L(u+v)<L。当j3<im,且仅2n-(2j2+2j3+2im)<L时,序列v以1×(28)n-im-1递增,即ε=1;当2n-(2j2+2j3+2im)<L时,序列v以3×(28)n-im-1递增,即ε=2;当时,序列v以7×(28)n-im-1递增,即ε=3;当2n-(2j3+2im)<L时,序列v以15×(28)n-im-1递增,即ε=4;当时,序列v以31×(28)n-im-1递增,即ε=5;当2n-(2j2+2im)<L时,序列v以63×(28)n-im-1递增,即ε=6;当2n-(2j1+2im)<L时,序列v以127×(28)n-im-1递增,即ε=7。
因为,当δ>0时,2n-(2j1+2j2+2i0+2j3)<L<L2(s(n))=2n-(2j1+2j2+2j3),即2n-(2j1+2j2+2i0+2j3)<2n-(2i1+2i2+…+2im)<2n-(2j1+2j2+2j3),则j3=im;又因当ε>0时,j3<im。所以δ,ε不能同时为正整数,即δ,ε中至少有一个为0。
特殊地,当ε=0,且δ=0时,对于∀u∈E,j2<ξ<j3,存在1个序列v,使L(u+v)=2n-(2j2+2ξ+2j3)<L,即λ=1;存在2个序列v,使L(u+v)=2n-(2j1+2ξ+2j3)<L,即λ=2。
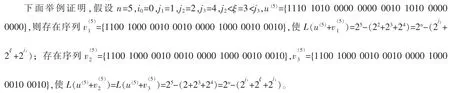
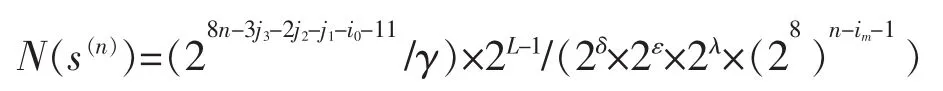

为了进一步验证定理4,下面举出一个例子,其正确性已用计算机程序进行了验证。
例1n=5,i0=2,j1=0,j2=1,j3=3,i1=0,i2=1,i3=2,i4=4。L=L8(s(n))=2n-(2i1+2i2+2i3+2i4
)=25-(1+2+4+16)=9,因i0>j2,则γ=2;因2n-(2j1+2j2++2i0+2j3)=25-(1+2+4+8)=17>L,则δ=0;又因j3<i4,且2n-(2j3+2im)=25-(8+16)=8<L,则ε=3;因ε≠0,δ=0,则λ=0,则满足L(s(5))=28,L2(s(5))=21,L8(s(5))=9的周期为25的二元序列s(5)的个数为
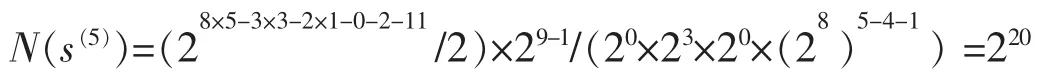
3 结语
文中给出以8错线性复杂度为第二下降点的所有可能取值形式,并推出具有2错线性复杂度和8错线性复杂度序列的完整计数公式。据文中的研究方法,可对其他具有第二下降点错线性复杂度序列进行研究,如k=6,其中2错线性复杂度为第一下降点,且6错线性复杂度为第二下降点。亦可研究以错线性复杂度为第三下降点的周期序列,如k=5,即以1错线性复杂度为第一下降点,3错复杂度为第二下降点,5错复杂度为第三下降点。
[1]Games R A,Chan A H.A fast algorithm for determining the complexity of a binary sequence with period 2n[J].IEEE Trans on Information Theory,1983,29(1):144-146.
[2]Ding C S,Xiao G Z,Shan W J.The Stability Theory of Stream Ciphers[M].Berlin/Heidelberg,Germany:Springer-Verlag,1991:85-88.
[3]Stamp M,Martin C F.An algorithm for the k-error linear complexity of binary sequences with period 2n[J].IEEE Trans.Inform.Theory,1993,39:1398-1401.
[4]Massey J L.Shift register synthesis and BCH decoding[J].IEEE Trans on Information Theory,1969,15(1):122-127.
[5]Etzion T,Kalouptsidis N,Kolokotronis N,et al.Properties of the error linear complexity spectrum[J].IEEE Transactions on Information Theory,2009,55(10):4681-4686.
[6]Kurosawa K,Sato F,Sakata T,et al.A relationship between linear complexity and k-error linear complexity[J].IEEE Transactions on Information Theory,2000,46(2):694-698.
[7]皮飞,戚文峰.二元周期序列的4-错线性复杂度[J].电子学报,2011,39(12):2914-2920.
[8]Meidl W.How many bits have to be changed to decrease the linear complexity?[J].Des Codes Cryptogr,2004,33:109-122.
[9]Zhou J Q,Liu W Q.On the k-error linear complexity for 2n-periodic binary sequences via Cube Theory[EB/OL].[2013-09-07].http://arxiv.org/ abs/1309.1829.
2n-periodic binary sequences with 8-error linear complexity as the second descent point
WANG Xifeng,ZHOU Xiaoming,ZHOU Jianqin
(School of Computer Science&Technology,Anhui University of Technology,Ma'anshan 243002,China)
Based on the structural approach and cube theory,we investigated the 2n-periodic binary sequences with 2-error linear complexity as the first descent point and 8-error linear complexity as the second descent point and analyzed the relationship between the first descent point and the second descent point.All the possible values of the 8-error linear complexity were given.Then we derived the complete counting functions of 2nperiodic binary sequences with 2-error linear complexity as the first descent point and 8-error linear complexity as the second descent point.With this method,2n-periodic binary sequences with k-error linear complexity as the second or third descent point can be obtained.
periodic sequence;linear complexity;k-error linear complexity;cube theory
TN918.1
A
1672-0687(2015)02-0056-09
责任编辑:艾淑艳
2014-05-06
安徽省自然科学基金资助项目(1208085MF106);安徽省教育厅自然科学研究项目(KY2013Z025);国家自然科学基金资助项目(61300059)
王喜凤(1980-),女,山东成武人,讲师,硕士,研究方向:通信,密码学与理论计算机科学。

