二根树指标马氏信源关于赌博系统的极限定理

顾小萍

（无锡市广播电视大学五年制高职部，江苏无锡214011）

二根树指标马氏信源关于赌博系统的极限定理

顾小萍

（无锡市广播电视大学五年制高职部，江苏无锡214011）

研究任意二根树图上二阶非齐次马氏信源的极限性质。通过构造相容分布和非负上鞅的方法，得到了任意无限连通二根树上二阶非齐次马氏信源关于广义赌博系统的一类广义渐近均匀分割性定理，也称广义Shannon-McMillan定理，并推广了已有的结果。

二阶非齐次马氏信源；二根树；Shannon-McMillan定理；广义赌博系统；相对熵密度

设T为一无限连通二根树图，σ，t（σ≠t）是T中任意两个顶点。则存在唯一的从σ到t的路径σ=x1，x2，…，xm=t，其中x1，x2，…，xm互不相同，且xi与xi+1为相邻两个顶点。m-1称为σ到t的距离。为给T中顶点编号，选定两个顶点作为根顶点（简称根），分别记为-1和o。如果一个顶点t位于根顶点o到顶点σ的唯一路径上，则记t≤σ。若σ，t为T上两个不同的顶点，记σ∧t为同时满足σ∧t≤σ和σ∧t≤t，且离根顶点o最远的顶点。

文中T表示任意局部有限无穷二根树。为了更好地解释二根树的概念，笔者以二根Cayley树TC，N为例，即除根顶点－1外，每个顶点均有N+1个顶点相连，如图1所示。记t为T中从根顶点o向上，从左向右数第t个顶点，记|t|为顶点t到根o的距离，若|t|=n，则t位于二根树的第n层。记T（n）表示从根o到第n层所有顶点的子图，Ln表示第n层上所有顶点的集合，表示T从第m层到第n层上所有顶点的集合。对于任意顶点t，从根顶点o到顶点t的路径上存在唯一一个离顶点t最近的顶点称为t的第一代父代，记为1t，且称t为1t子代，t的第二代父代记为2t。类似的，t的第n代父代记为nt。设B是树图T的子图，记XB={Xt，t∈B}，且xB为XB的实现。

定义1设G={s1，s2，…，sM}为一有限状态空间，{Xt，t∈T}是定义在概率空间{Ω，F，P}上且于G中取值的随机变量集合。设

图1 二根树TC，3

分别为定义在G2上的二维概率分布和G3上的二阶随机转移矩阵族，如果对于任意顶点t，

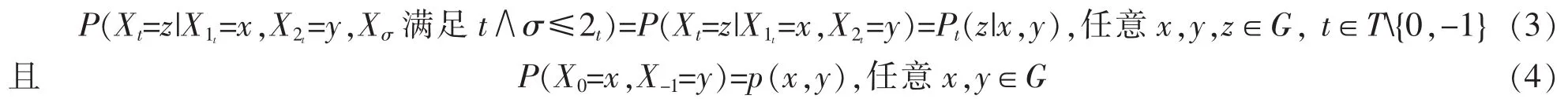
则称{Xt，t∈T}为具有二维初始分布p和二阶转移矩阵族P的G值树指标二阶非齐次马氏链。

由（1），（2）式可得树指标二阶非齐次马氏链的联合分布为

这里|T（n）|表示从第－1层到第n层的所有顶点的个数，则称fn（ω）为树T的子图T（n）上关于测度P的相对熵密度。

在概率论和信息论当中，fn（ω）的收敛性具有重要的理论和实际意义。fn（ω）在一定意义下的收敛（L1收敛，依概率收敛，a.s.收敛）称为Shannon-Mcmillan定理或信源的渐近均匀分割性（AEP）。关于整数集上信源的Shannon-Mcmillan定理已有广泛和深入的研究[1-2]。近几年来，由于信息论发展的需要，人们开始研究树图随机场的Shannon-Mcmillan定理[3]。树图模型近年来已引起物理学、概率论及信息论界的广泛兴趣。Berger与叶中行[4]研究了齐次树图上某些平稳随机场的熵率。叶中行与Berger[5]又研究了齐次树图上PPG不变随机场的遍历性与渐近均匀分割性。但他们的收敛结果只涉及依概率收敛。杨卫国，叶中行[6-7]近年来研究了齐次树指标与Cayley树指标马氏链场上a.s.收敛的Shannon-Mcmillan定理。但杨，叶的结果仅涉及单根树图马氏链场情况，而对赌博系统中二根树指标马氏链场的Shannon-Mcmillan定理没有考虑。最近，彭伟才和杨卫国[8]研究了齐次树指标随机场关于马氏链场泛函的小偏差定理，石志岩与杨卫国[9]研究了m根Cayley树上m阶非齐次马氏链场的若干极限性质，杨卫国[10]又研究了任意随机序列几乎处处收敛的一些极限性质。

定义2给出树上广义随机选择的概念，先给出一组定义在Sn（n=1，2，…）上并取值于区间[0，b]的非负实值函数列fn（x1，…，xn）。

令Y0=y（y为任意实数），Yt=f|t|（X1t，X2t，…，X0，X－1），|t|≥2。其中|t|代表从顶点t到根顶点-1的边数或者距离。fn（x1，…，xn）称为广义随机选择函数，{Yt，t∈T{0，－1}}称为二根树指标广义赌博系统或广义随机选择系统，传统的链式赌博系统{Yn，n≥0}在两点集{0，1}中取值。

定义3设{Xt，t∈T}如上定义的树指标二阶非齐次马氏链，{Yt，t∈T{0，－1}}为如上定义的广义随机选择系统，称

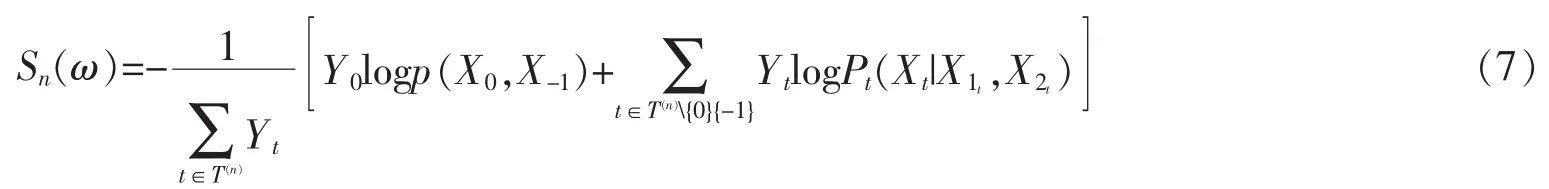
为树指标二阶非齐次马氏链{Xt，t∈T}关于广义随机选择系统的相对熵密度，也称其为广义相对熵密度。显然，当Yt≡1，t∈T（n）时，该广义相对熵密度即为一般的相对熵密度。

该文笔者将文献[7]的结果推广到任意局部有限无穷二根树上广义随机选择系统的情况。即通过构造相容分布和非负鞅的方法，研究二根树上二阶非齐次马氏信源关于赌博系统的一类广义Shannon-McMillan定理。并由此得出已有的树上非齐次马氏信源的Shannon-McMillan定理。文中将文献[11]中所用的方法加以改进，并作为推论得到了文献[7]的主要结果。

1 主要结果及证明

定义4设

称Ht（Xt|X1t，X2t）为Xt关于X1t，X2t的随机条件熵。

定理1设{Xt，t∈T}是如上定义的任意无穷连通二根树指标二阶非齐次马氏信源，{Yt，t∈T{0，－1}}为二根树指标广义随机选择系统。Sn（ω）与Ht（Xt|X1t，X2t）分别由（7）与（8）式定义。设

则有

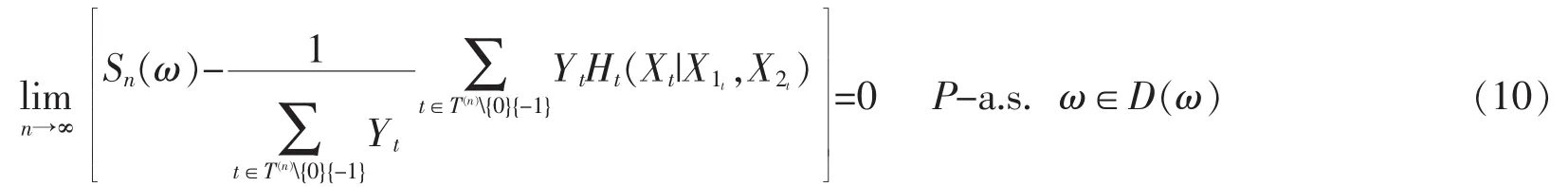
推论1设{Xt，t∈T}是如上定义的树指标二阶非齐次马氏信源，为二根树指标广义随机选择系统。fn（ω）与Ht（Xt|X1t，X2t）分别由（6）与（8）式定义。则有

证明在定理1中令Yt≡1，t∈T（n）{0}{－1}，则有。从而可知D（ω）＝Ω，由（10）式可得推论1成立。

注在推论1中当{Xt，t∈T}退化为单根树指标一阶非齐次马氏信源时，有

这时，推论1即为Yang and Ye[7]的定理2。

证明考虑概率空间{Ω，F，P}，设λ∈（－1，1）。设δj（·）表示Kronecker函数，即δi（j）=δij（i，j∈S）。并记gk（j）=-logPt（j|X1t，X2t），构造如下的乘积分布

由（11）式，令

由（5），（11）与（12）式有

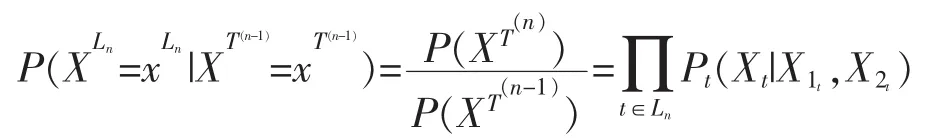
因而，有

由Doob鞅收敛定理[12]可知{Un（λ，ω），Fn，n≥1}是一非负上鞅。且有

由（9）与（15）式，有

又由（13）与（16）式有

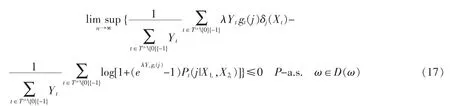
由（17）式及上极限的性质与不等式：1-1/x≤lnx≤x-1（x＞0），ex-1-x≤（1/2）x2e|x|

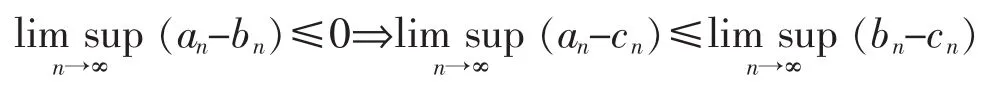
又注意到gt（j）=-logPt（j|X1t，X2t），有

设0＜λ＜1，由（18）式有

考虑函数

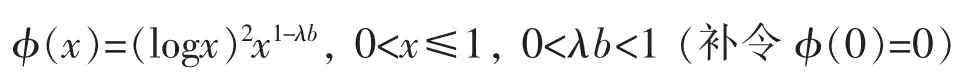
求导得

令φ′（x）=0得x＝e2/（λb-1），故φ（x）在[0，1]区间上的最大值为

由（21）与（19）式，当0＜λ＜1时有

取0＜λi＜1（i=1，2，…），使得λi→0+（i→∞），则对一切i，由（22）式有

由（7），（8）与（23）式以及gt（j）=-logPt（j|X1t，X2t），有

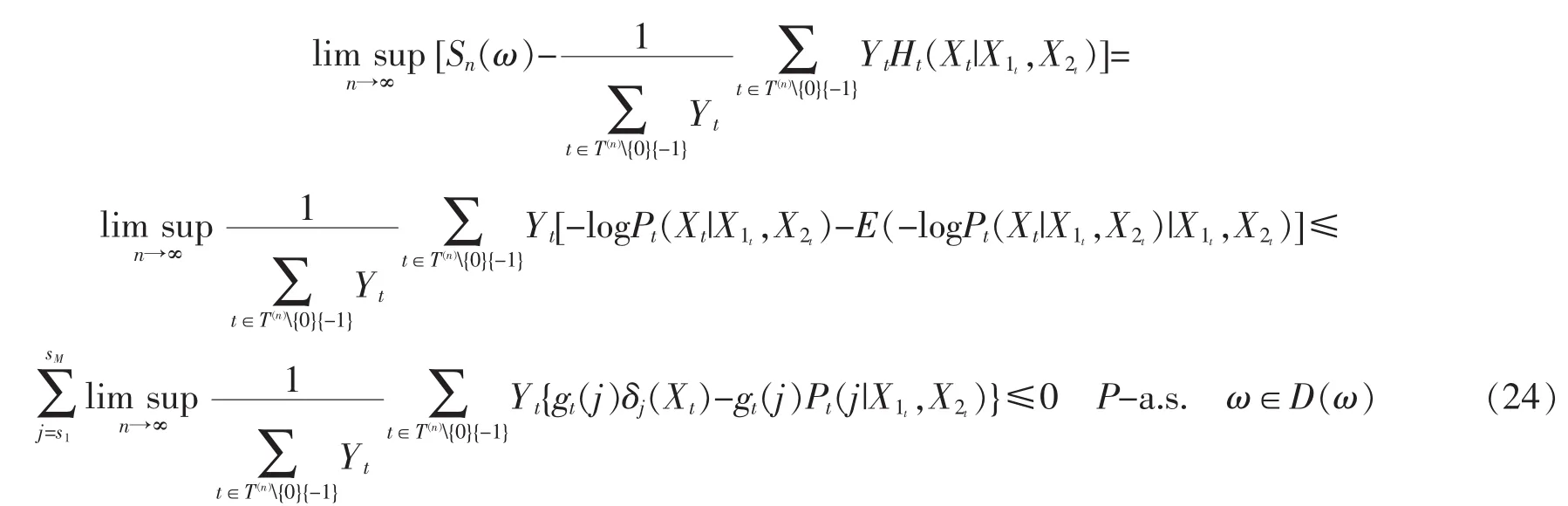
当-1＜λ＜0时，由（18）式有

这时，由（21）和（25）式有

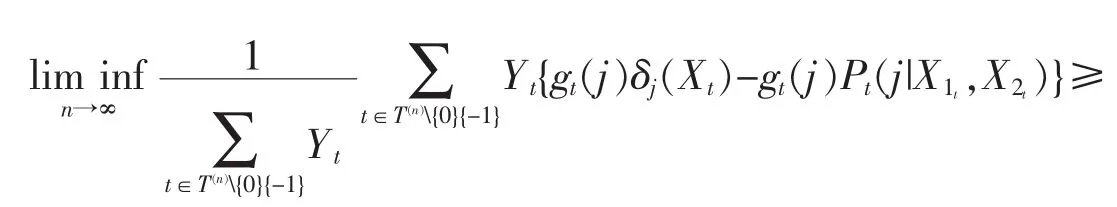
取-1＜λi＜0（i=1，2，…），使得λi→0-（i→∞），则对一切i，由（26）式有

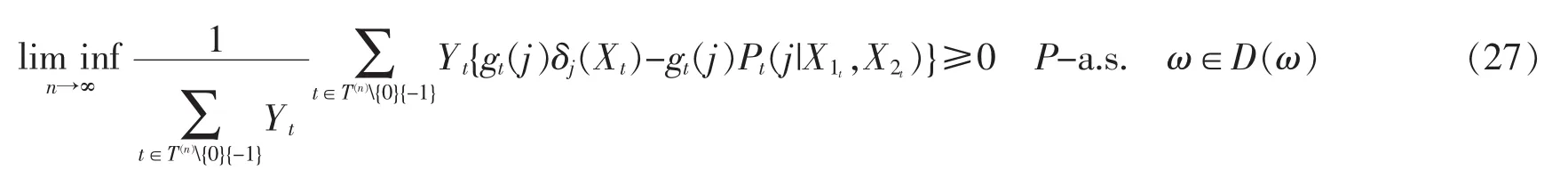
由（7），（8）与（27）式以及gt（j）=-logPt（j|X1t，X2t），类似于（24）式的推导过程，有

由（24）与（28）式有

于是（10）式成立。

2 结语

通过构造非负上鞅和相容分布的方法，研究了任意局部有限二根树指标二阶非齐次非齐次马氏链关于广义赌博系统的熵定理，即Shannon-McMillan定理，推广了已有的结果。树形图上的信息熵定理目前国内外的研究结果较少，文中的结果对于树形图上的信息论编码理论具有一定的指导意义。

[1]刘文，杨卫国.任意信源二元函数一类平均值的极限性质[J].应用概率统计，1995，11（2）：195-203.

[2]刘文，杨卫国.任意信源与马氏信源的比较及小偏差定理[J].数学学报，1997，40（1）：22-36.

[3]Ye Z，Berger T.Asymptotic equipartition property for random fields on trees[J].Chinese J Appl Probab Stst，1993（9）：296-309.

[4]Berger T，Ye，Z.Entropic aspects of random fields on trees[J].IEEE Trans Inform Theory，1990，36（5）：1006-1018.

[5]Ye Z，Berger T.Ergodic regularity and asymptotic equipartition property of random fields on trees[J].Combin Inform System Sci，1996，21（2）：157-184.

[6]Yang W G.Some limit properties for Markov chains indexed by homogeneous tree[J].Stat Probab Letts，2003，65：241-250.

[7]Yang W G，Ye Z.The asymptotic equipartition property for nonhomogeneous Markov chains indexed by a homogeneous tree[J].IEEE Trans Inform Theory，2007，53：3275-3280.

[8]Peng W C，Yang W G，Wang B.A class of small deviation theorems for functionals of random fields on a homogeneous tree[J].Journal of Mathematical Analysis and Applications，2010，361：293-301.

[9]Shi Z Y，Yang W G.Some limit properties for the mth-order nonhomogeneous Markov chains indexed by an m rooted Cayley tree[J].Statistics& Probability Letters，2010（15－16）：1223-1233.

[10]Yang W G，Tao L L，Cheng X J.On the almost everywhere convergence for arbitrary stochastic sequence[J].Acta Mathematica Scientia，2014，34：1634-1642.

[11]Liu W，Wang L Y.The Markov approximation of the random fields on Cayley tree and a class of small deviation theorems[J].Stat Probab Letts，2003，63：113-121.

[12]Chung K L.A Course in Probability Theory[M].New York：Academic Press，1974.

Limit theorems for Markov information source on gambling systems indexed by a double rooted tree

GU Xiaoping
（Department of Higher Vocational，Wuxi radio and TV University，Wuxi 214011，China）

This paper aims to study some limit properties of second-order nonhomogeneous Markov information source indexed by a double rooted tree.By constructing the consistent distribution and nonnegative super-martingale,the author obtained a class of generalized Shannon-McMillan theorems for the second-order nonhomogeneous Markov information source indexed by a double rooted tree on the generalized gambling system.And the existed results were generalized.

second-order nonhomogeneous Markov information source；double rooted tree；Shannon-McMillan theorem；generalized gambling system；relative entropy density

O211.6MR（2000）Subject Classification：60F15

A

1672－0687（2015）02－0024－06

责任编辑：谢金春

2014－09－05

江苏城市职业学院“十二五”规划课题项目（12SEW-Y-039）

顾小萍（1979-），女，江苏无锡人，讲师，硕士，研究方向：概率论。