一种多传感器的盲区边缘定位精度改进的算法
左晓敏,李金厚,刘辉,张学峰
(安徽工业大学计算机科学与技术学院,安徽马鞍山243002)
一种多传感器的盲区边缘定位精度改进的算法
左晓敏,李金厚,刘辉,张学峰
(安徽工业大学计算机科学与技术学院,安徽马鞍山243002)
针对多传感器观测盲区两侧边缘处出现误差较大现象,提出基于阈值的盲区两侧附近异常数据的检测方法。对原有数据沿x轴、y轴方向进行正交分解,分别选取检测这两个方向分量上异常数据的阈值。在此基础上,对原有数据进行筛选,然后通过适当的填补方法,依次对这两个方向上剔除掉的数据进行填补,获得完整的数据集,以替代原有数据。仿真结果表明,采用新算法可以明显提高目标在盲区边缘附近的定位精度。
异常数据;检测;传感器;定位
在跟踪定位系统中,多传感器的数据融合,是对多传感器的原始信息利用信息融合技术进行处理,以达到实现高性能的跟踪定位效果。但由于传感器的系统偏差和随机误差的存在,在目标跟踪系统中,目标的定位计算受到很大的影响。其中,现有的滤波方法可以消除随机误差,而系统误差,因为具有确定性,所以滤波方法无法将其去除[1]。需要事先对系统误差进行估计,再对后续的传感器配准进行补偿,这一过程称为误差配准[2]。传感器数据融合技术的发展离不开传感误差配准技术的发展,后者为前者提供技术保障。现如今这种技术已成为传感器配准研究中的热点问题,同时也是难点问题[3-4]。
在解决传感器固定偏差情况下的配准,Okello.N和Ristic.B在Maximum likelihood registration for multiple dissimilar sensors中提出—种离线的极大似然配准算法[5],这种算法与传统偏差估计方法(如最小二乘法和极大似然估计法)相比,优势在于不强调传感器需要配对组合之后使用。不足在于要求明确传感器时钟完全同步,并且知道传感器的精确位置[6]。
祁永庆提出基于信息融合的修正极大似然配准算法[7]。采用了冗余信息补偿方法处理被动传感器在观测盲区内目标不可观测的问题。但由于具有不同配准偏差的传感器存在,在数据采集过程中容易产生粗大误差,导致在传感器观测盲区两侧的边缘处,定位轨迹上会显现少许的间隔或重叠误差较大情况。
在定位盲区两侧边缘处目标跟踪航迹出现的间隔和重叠等偏差较大的问题,将粗大误差较大的数据视为异常数据。在检测异常数据研究上,许多学者做出了重大的贡献,发现了许多有效的算法。学者乐立利针对双参数对数正态分布下情况提出相应的异常数据检测算法[8]。肖瑛[9]首次将3σ准则应用到检测异常数据方面。尽管前人在异常数据检测算法上取得很大的研究成果,但应用改善多传感器观测盲区边缘处定位效果上效果不佳。
1 基本误差配准数据的获取
根据祁永庆在文献[6]第三章中关于基于信息融合的修正极大似然配准算法及其仿真模型,获取定位结果如图1所示。

图1 目标定位轨迹与真实轨迹对比
在图1目标定位轨迹图中,可以看出修正极大似然配准算法对目标状态的定位已经很逼近,但在其中两传感器之间的连线(盲区)附近,目标的定位出现误差较大现象,也就是在其论文第三章仿真分析中提到的盲区边缘处仍然存在少许间断和重叠情况[7]。为此,文中将对两两传感器附近的数据做进一步处理,以达到定位误差的再次降低。
2 异常数据的处理方法
2.1 异常数据的检测
由第1节中得到的的误差配准数据,作为待处理的初始数据,记为:。
针对正弦曲线和直线这类曲线,可知在这连续曲线上的点,同一固定的点(如观测站)间的距离的差值,这种差值之间的波动大小会保持平缓地变化。如果出现较周围附近的点变化幅度较大情况,则将其视为异常数据。然而针对目标的轨迹曲线是其他类型曲线时,原理是相同。
文中以此为依据,提出检测异常数据阈值的一种方法。图2为x方向分量检测异常数据示意图,观测站S对目标在k时刻的位置Ak的测量距离为,观测站S对目标在k+1时刻的位置Ak+1的测量距离为,其中,k=1,…,N-1;前后两个时刻的距离差值,其中,k1=2,…,N;距离差值的波动大小,其中,k2=3,…,N;如果满足条件,则Ak+1点可判断为含误差的数据,应予剔除,所以,把作为新的判别异常数据的判据。

图2 异常数据检测示意图
基于该方法的剔除步骤如下:
(1)选取一个观测站S(ξ1,η1),令其x方向位置为固定点S(ξ1,0);
(2)计算测量距离差值的波动值
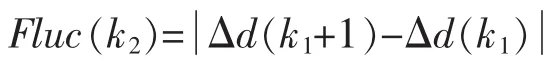
(3)选取门槛值εx,大量仿真试验,调试选取使定位精度最高的门槛值;
(5)同理,可以得到y方向分量。
2.2 门槛值选取
x,y方向上,目标轨迹曲线上不同时刻的点与固定的观测站间的距离的差值,这种差值之间的波动大小如图3。
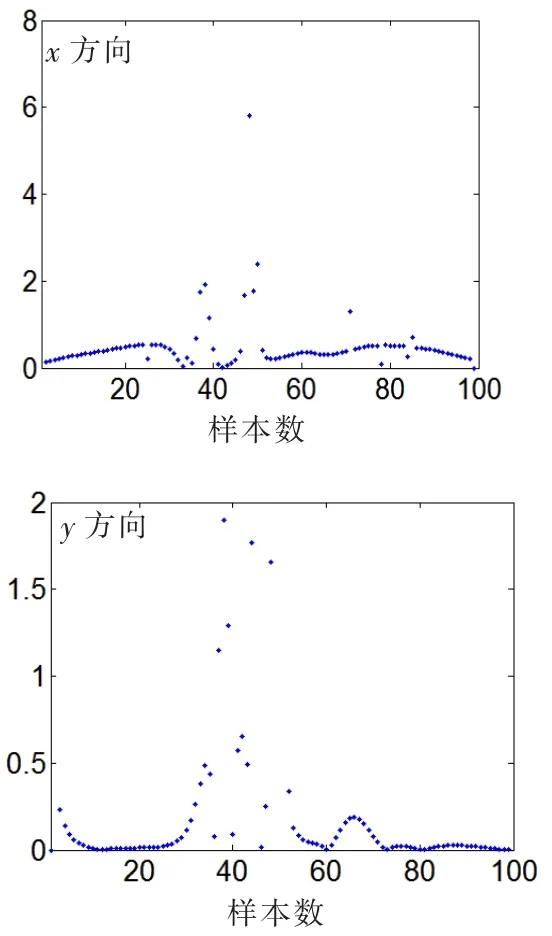
图3 前后两点间距离的差值图
在图3中,根据波动大小数值来选取用于筛选异常数据的门槛值。
门槛值εx,εy在取不同的值的情况下,将含有配准误差的数据进行筛选,针对剔除后剩下的数据,运用现有的代数多项式拟合方法,获取完整的数据集[10]。
图4(a),(b)所示,在不同的数据集的情况下,x,y两个方向上数据的均方根误差值(RMSE)变化很大,这表明了门槛值选取对获取具有最小均方根误差值的数据集具有直接作用,同时对缩小目标在盲区边缘处的定位误差,也将具有良好的效果。
在图4中,比较两个方向分量上的均方根误差值(RMSE),选取最低均方根误差值,以及相应的筛选这些数据的门槛值参数。其中门槛值参数用于后续的仿真计算。
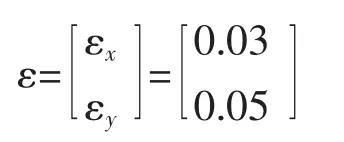

图4 不同门槛值下的RMSE值
3 算法流程图(如图5)
以x方向上分量处理方法为例,针对估计出的含有误差的配准数据,将其作为待处理的数据,在此基础上采用文中的异常数据检测方法,对配准后的数据进行处理,进而更新目标的定位信息。
同理,可更新y方向上分量的状态信息。与修正的极大似然配准算法的区别在于:笔者需要从其x,y两个方向上分量判别配准后的目标轨迹前一时刻与后一时刻同观测站的距离差值的波动大小,决定是否剔除。如果剔除,将通过对筛选出符合条件的数据集进行多项式拟合,实现了将缺失的数据填补完整,最终重新确定完备数据,更新目标状态信息。
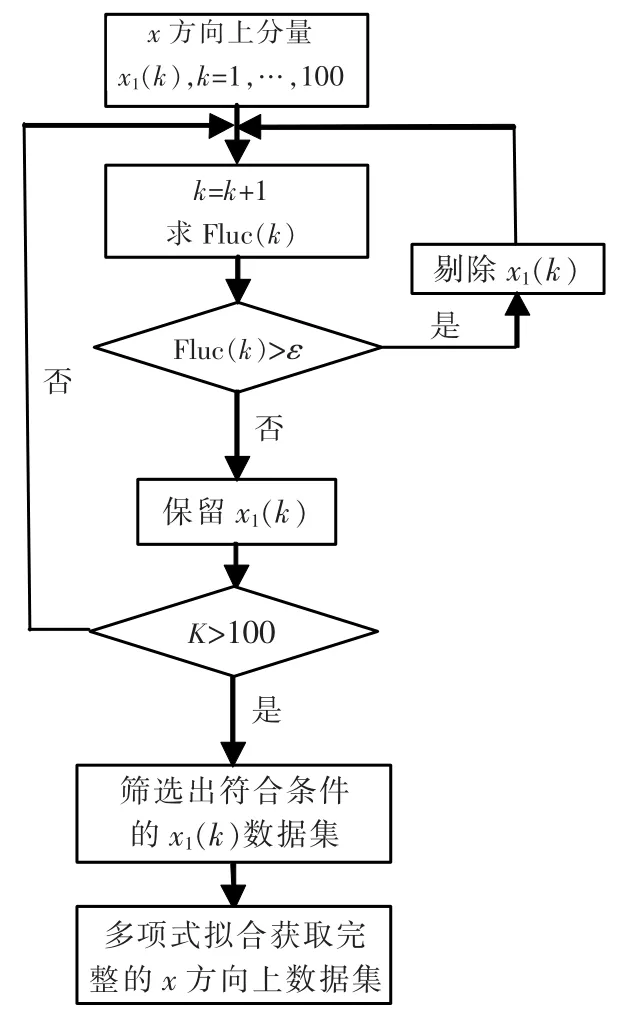
图5 新算法流程图(x方向分量为例)
4 仿真计算结果及分析
考虑由3个被动传感器构成的多平台系统,假定传感器是同步的,传感器的坐标是固定的且是已知的。若仅考虑二维平面,则被动传感器都是一维的,仅测量目标的方位角。目标的真实航迹的状态方程为[3]:x1(k)=135+150sin(0.06k),y1(k)=30-5k。其中,k=1,…,N,(N=100)。传感器的坐标分别为S1=(0,-200),S2=(300,-200),S3=(80,-75),单位为km。偏差分别为Δθ1= -7.0°,Δθ2=7.0°,Δθ3=-4.0°。测量噪声的标准方差分别为°
4.1 定位结果比较
新方法得到的目标轨迹与修正极大似然配准算法(modified MLR)的相应轨迹对比如图6所示。其中,“-.-”点画线为真实目标轨迹曲线;“--”长虚线表示修正极大似然配准算法的轨迹曲线;实线表示为新方法定位轨迹曲线。
由图6不难看出,当目标接近传感器观测盲区时,其附近的边缘处出现的间隔现象也明显减少,这一仿真结果充分验证了新方法的定位轨迹更逼近真实轨迹。
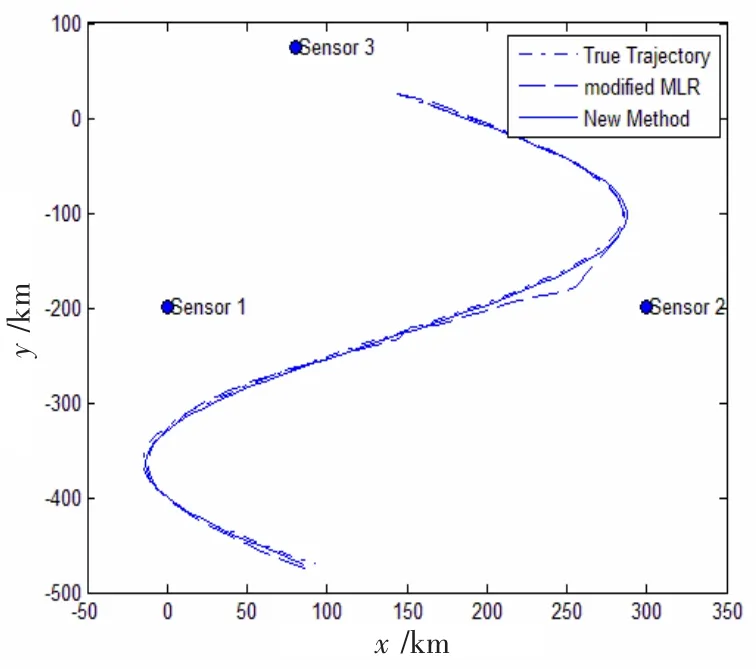
图6 两种方法完整定位轨迹比较
4.2 定位误差比较
新方法处理后的目标的完整的定位数据误差情况如图7所示。其中“-.-”点画线表示新方法定位误差;实线表示修正极大似然配准算法的定位误差。
由图7可知,随着采样次数的增加,新方法比祁的修正极大似然配准算法的定位精度更高,尤其是在采样时刻30-50之间,也就是传感器的观测盲区附近,误差降低更加明显。因而,笔者提出的采用新判据剔除了含误差配准数据中的异常数据的方法,有效地提高了传感器观测盲区两侧的边缘处的定位精度。
5 结语
文中提高配准精度的新改进算法是针对盲区两侧边缘处目标跟踪航迹重叠和间隔的问题提出的,其核心思想是利用目标轨迹前一时刻与后一时刻同观测的距离差值的波动情况,将筛选出的异常数据剔除,然后通过适当的回归填补法,对两个方向上的数据进行更新,重新获得传感器的目标状态。仿真结果表明,新算法提高了传感器观测盲区两侧边缘处的定位精度。
[1]张志云,周永丰.基于最小二乘和广义最小二乘的系统偏差估计研究[J].舰船电子工程,2008,28(8):89-91.
[2]何友,修建娟,张晶炜,等.雷达数据处理及应用[M].2版.北京:电子工业出版社,2009.
[3]何友,王国宏.关欣信息融合理论及应用[M].北京:电子工业出版社,2010.
[4]宋强,何友,熊伟.基于极大似然的单传感器误差配准算法[J].宇航学报,2011,32(8):1824-1833.
[5]Okello N,Ristic B.Maximum likelihood registration for multiple dissimilar sensors[J].IEEE Transactions on Aerospace and Electronic systems,2003,39(3):1074-1083.
[6]祁永庆.多平台多传感器配准算法研究[D].上海:上海交通大学,2008.
[7]祁永庆,敬忠良,胡士强.基于信息融合的修正极大似然配准方法[J].中国光学快报,2007,5(11):639-641.
[8]乐立利,曾海群.双参数对数正态分布异常数据的检测方法[J].数学理论与应用,2009,29(1):29-32.
[9]肖瑛,董玉华.基于小波网络的遥测视速度异常数据剔除方法[J].大连民族学院学报,2009,11(3):215-218,281.
[10]侯贺.缺失数据处理方法的研究及其在软测量技术中的应用[D].沈阳:东北大学,2011.
An improved multi-sensor algorithm for higher position-accuracy near the blind spots
ZUO Xiaomin,LI Jinhou,LIU Hui,ZHANG Xuefeng
(School of Computer Science&Technology,Anhui University of Technology,Ma'anshan 243002,China)
Aiming at the phenomenon that the error becomes larger when the target occurs on either side of the blind spots of the multi-sensor,we have proposed a method detecting the outlier near either side of the blind spots based on the threshold.Along the x axis and y axis,the original data was divided into two groups based on orthogonal decomposition.Then two thresholds were selected to detect the outliers separately.On the basis of this analysis,the original data was discriminated.And then the proper imputation methods were selected to deal with the missing data and get the complete data set.The original data were replaced with the new complete data.Simulation results show that the accuracy of the target positioning near the blind spots can be obviously improved by using this proposed algorithm.
outlier;detection;sensor;position
TP274;TN957
A
1672-0687(2015)02-0065-04
责任编辑:艾淑艳
2014-07-08
安徽省自然科学基金资助项目(1308085QF113)
左晓敏(1989-),女,江苏连云港人,硕士研究生,研究方向:传感器定位,异常数据检测。

