基于粒矩阵的多输入多输出真值表快速并行约简算法

陈泽华马 贺

（太原理工大学信息工程学院 太原 030024）

基于粒矩阵的多输入多输出真值表快速并行约简算法

陈泽华*马 贺

（太原理工大学信息工程学院 太原 030024）

真值表是表征逻辑输入与输出之间因果关系的重要工具，真值表约简在数字逻辑电路的分析与设计中具有重要意义。该文将真值表看作逻辑信息系统，将真值表约简转化为逻辑信息系统的最简规则获取。采用粒计算分层粒化的思想，在不同粒度下，利用粒矩阵的知识表示形式、粒矩阵中的启发式知识以及粒矩阵运算，设计了多输入多输出真值表快速并行约简算法。以发光二极管七段数字显示器为例进行了算法说明，通过数学证明和算法复杂性分析证明了算法的正确性和有效性。

数字逻辑电路；真值表；粒度；粒矩阵；并行约简；粒计算

1 引言

真值表约简在数字逻辑电路分析与设计中具有重要作用。经典方法有卡诺图法、公式法、Q-M及其改进算法以及立方体算法等［17］-。当输入变量增大时，前3种方法算法复杂度比较高，不利于程序实现，而且不能对多个输出进行并行处理。立方体算法［2］相对简单，可以处理多输出，本质依然依靠逻辑代数运算规律。目前，真值表约简算法被内嵌在国外的电子设计自动化软件中，工程师们不再需要自行设计约简算法。因此，国内外对真值表的约简问题研究成果仍然停留在十几年前。

粒计算［8］求解复杂问题的思想和方法受到关注，基于粒计算的信息系统知识处理方法得到快速发展［915］-。文献［16］将真值表看作逻辑信息系统，从知识工程角度分析真值表，将真值表看作等价关系的粒计算模型，通过分层粒化、矩阵运算，将传统的真值表化简过程转化为基于粒矩阵运算的逻辑信息系统的最简规则提取过程。

本文进一步优化了文献［16］中的粒矩阵运算，通过定理1减少了矩阵的存储规模、提高了算法的搜索效率，并将其扩展为多输入多输出（M IMO）真值表快速并行约简算法。本文以发光二极管七段数字显示器为例，详述了算法步骤。最后通过数学推导，证明了本文算法与传统卡诺图约简算法的等价性。通过理论分析，探讨了算法的复杂性和有效性。

2 预备知识

定义1 真值表、最小项表达式、最简逻辑函数表达式［1-3］：真值表是表征逻辑事件输入和输出之间全部可能状态的表格，是逻辑因果关系的表格表示。当一个真值表同时有多个输出时，称为多输出真值表。真值表中全部m个输入变量的乘积项（每个变量只以原变量或反变量的形式出现一次）称为最小项。真值表中所有逻辑函数值为1的最小项之和称为最小项表达式。简化后的真值表中所有输出值为1的输入变量乘积项的和称为最简逻辑函数表达式。

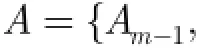
注：在下文中用黑体 Xi表示矩阵或向量，用Xi表示等价关系或等价类。

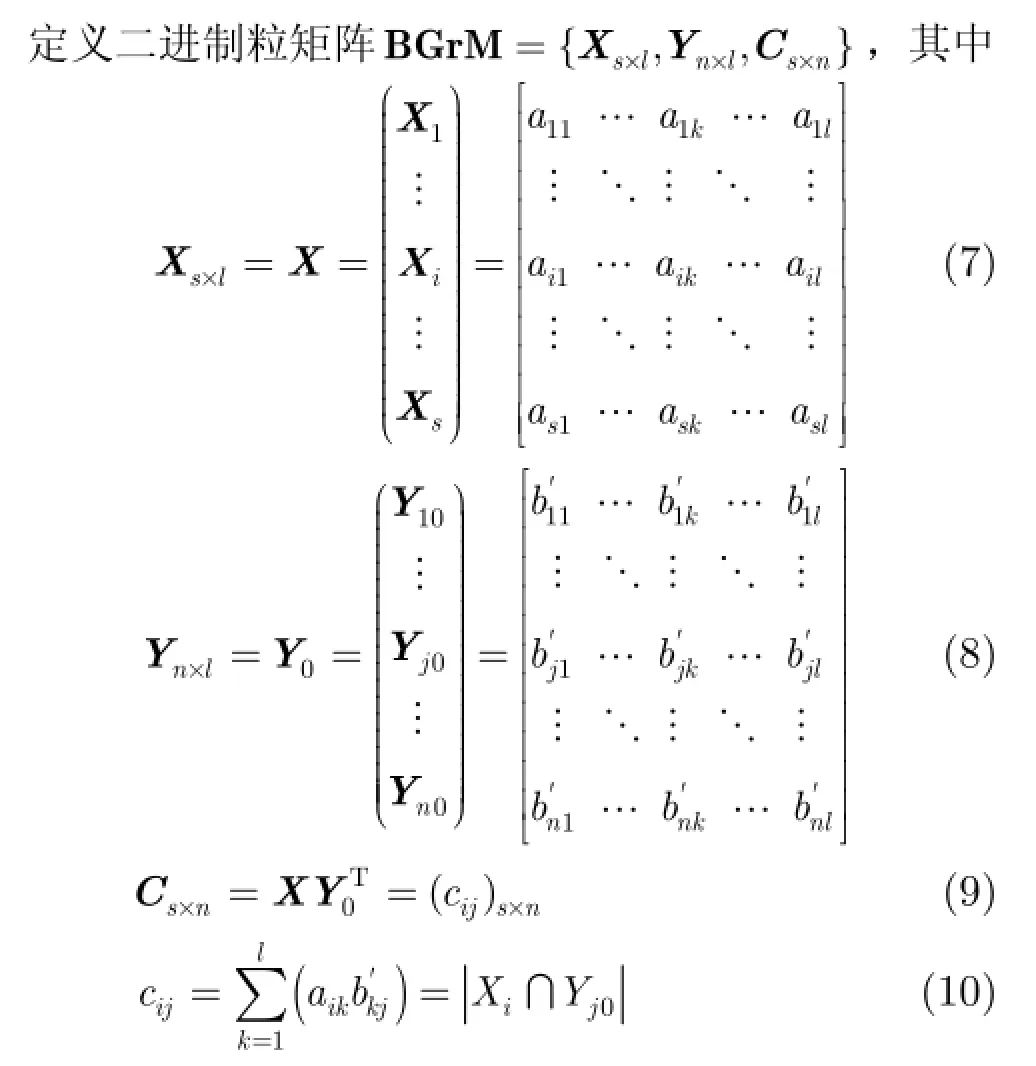
矩阵X表示输入变量组合A'导出的等价类集合，矩阵Y0由全部n个输出的“0”输出向量构成。矩阵Cs×n（下文简称C ）反映了所有等价类Xi与Yj1之间的包含关系，称为矩阵X与Y的粒逻辑关系矩阵。·表示集合的势。

下面通过定理1说明粒逻辑关系矩阵所表达的信息与含义：

3 多输入多输出真值表快速并行约简算法

3.1 符号定义

3.2 算法描述

区别于传统的任何一种算法，基于粒计算的多输入多输出（m输入n输出）真值表快速并行约简算法的主要思想是：从知识工程的角度，从粗到细，在不同粒度空间下对逻辑信息系统进行约简，约简的本质是借用代数规则和统计规律为启发式信息，通过粒矩阵运算，用最少的输入变量和变量值快速辨识出所有输出属性中所有的属性值1。算法描述如表1所示。

3.3 计算实例

例1 数字显示译码器［3］

发光二极管七段数字显示器通常采用七段（a， b，c， d， e， f， g）字形显示，如图1所示。表2给出一种七段译码器的功能表，它接收8421BCD码，输出逻辑值为1时，对应的字段点亮，输出为0时，对应的字段熄灭。显示的字形图如图2所示。

表1 基于粒计算的多输入多输出真值表快速并行约简算法

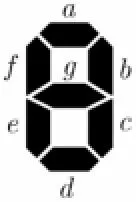
图1 七段字形显示

图2 十进制数字

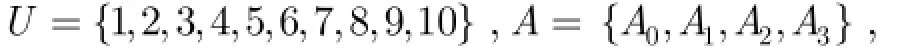
（1）设置初始值ω=1，此时粒度最粗。下文用i表示Ai，可以得到

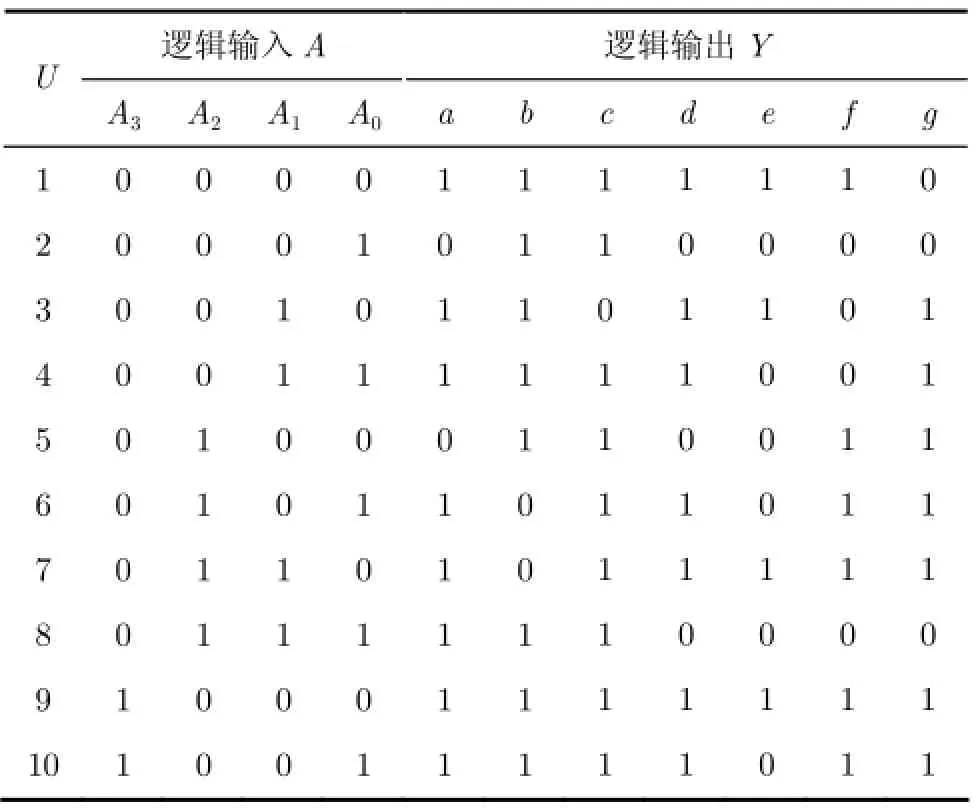
表2 七段译码器的逻辑信息系统

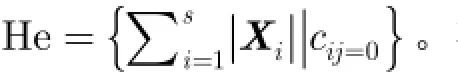
根据He的大小对Xω=1进行排序，见表3，其中灰色规则表示重复识别的规则，不做记录。此时ob ja=｛3，4，7，8，9，10｝， ob jb=｛1，2，3，4，9，10｝，均未完全区分输出中的1，继续计算。

（2）在细粒度ω=2上继续计算：

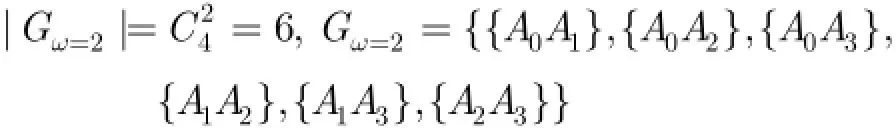
可得

表3 ω1=的计算过程

计算并根据He的大小对Xω=2进行排序，见表4。表4中灰色的规则表示其分辨出来的行已经被包含在ob j中，不做记录。由于本次计算至Xω=2中的前3个 Xi就已经完成了运算。因此表4只列出了这3个 Xi。

表4 ω2=的计算过程

4 算法分析

4.1 算法正确性证明

在单输出情况下，本算法与卡诺图约简算法等价。证明如下：

等价性证明保证了本文算法的正确性。

4.2 算法复杂性分析

4.3 无关项的处理

当真值表含有无关项时，应用卡诺图法、Q-M算法和立方体算法时，无关项通常被假设为1参与运算，最后需要验证无关项是否构成冗余项，如果是则删除，否则留下得到最终结果。将真值表当作LIS进行处理，不需要对无关项的输出做任何假设，通过设定粒度，会自动按需将无关项放入卡诺图法对应的大圈中，化简结果不受影响。

5 结束语

Q-M算法及其改进算法本质是卡诺图方法的扩展。立方体方法本质依据逻辑运算规则［2］。本文提出的基于粒矩阵的真值表快速并行约简算法，本质上是从信息处理角度在不同粒度空间下实现逻辑规则的并行约简，在思路上与传统方法不同，在算法上还有进一步优化的空间。

本文创新之处在于：（1）将真值表当作逻辑信息系统，在不同的粒度空间，通过定义粒矩阵及其基本运算，并行实现逻辑规则化简；（2）利用二值逻辑特性，将文献［16］中寻找矩阵中的NE（i）=1转变为寻找cij=0，减小了相关的数值比较和搜索，并将输出矩阵规模减半，从而降低了算法的空间复杂度和时间复杂度；（3）通过矩阵运算并设置启发式算子和终止条件，并行得到所有输出的逻辑化简，提高了计算效率；（4）不需要单独考虑无关项；（5）证明了本文算法与经典的卡诺约简方法是等价的。以上几点决定了本文算法的快速性和可靠性。

真值表化简是数字逻辑电路分析和设计中的重要问题，本文将等价关系的粒计算模型应用于m输入n输出真值表化简，一方面丰富了粒计算理论研究，另一方面为数字逻辑电路的分析与设计提供了新思路。如何将二元关系的粒计算模型［17］推广到时序逻辑电路中的状态转移表（图）的化简是我们正在进行的工作。

［1］ 阎石. 数字电子技术基础［M］. 第5版， 北京: 高教出版社，2006: 29-54.Yan Shi. Fundamentals of Digital Electronics［M］. 5th Edition，Beijing: Higher Education Press， 2006: 29-54.

［2］ 边计年， 薛宏熙， 苏明， 等. 数字系统设计自动化［M］. 第2版北京: 清华大学出版社， 2005: 221-226. Bian Ji-nian， Xue Hong-xi， Su M ing， et al.. Design Automation for Digital Systems［M］。 2nd Edition， Beijing: Tsinghua University Press， 2005: 221-226.

［3］ 刘宝琴. 数字电路与系统［M］. 第2版， 北京: 清华大学出版社，2007: 39-56. Liu Bao-qin. D igital Circu its and System s［M］. 2nd Ed ition，Beijing: Tsinghua University Press， 2007: 39-56.

［4］ Cepek O， Kucera P， and Kurik S. Boolean functions w ith long prime im plicants［J］. Information Processing Letters， 2013，113（19-21）: 698-703.

［5］ Dusa A. A m athem atical app roach to the boolean m in im ization p rob lem［OL］. http://www.com passs.org/ wpseries/Dusa2007a.pdf， 2010.

［6］ Altun M and Marc D. Riedel: lattice-based computation of Boolean functions［OL］. http://www.m riedel.ece.umn.edu/ w iki/images/7/7b/A ltun_Riedel_Lattice-Based_Com putat ion_of_Boolean_Functions.pd f， 2010.

［7］ Hemaspaandra E and Schnoor H. M inimization for generalized Boolean formulas［OL］. http://arxiv.org/pdf/ 1104.2312.pd f， 2011.

［8］ Zadeh L A. Some reflections on soft com puting， granular com puting and their roles in the conception， design and utilization of information/intelligent system s［J］. Soft Com puting， 1998（2）: 23-25.

［9］ 苗夺谦， 徐菲菲， 姚一豫. 粒计算的集合论描述［J］. 计算机学报， 2012， 35（2）: 351-363. M iao Duo-qian， Xu Fei-fei， and Yao Yi-yu. Set-theoretic formulation of granular com puting［J］. Chinese Journal of Computers， 2012， 35（2）: 351-363.

［10］ 张清华， 幸禹可， 周玉华. 基于粒计算的增量式知识获取方法［J］. 电子与信息学报， 2011， 33（2）: 435-441. Zhang Qing-hua， Xing Yu-ke， and Zhou Yu-hua. The incremental know ledge acquisition algorithm based on granular com puting［J］. Journal of Electronics & Information Technology， 2011， 33（2）: 435-441.

［11］ Qian Yu-hua， Hu Zhang， Sang Yan-li， et al.. M ultigranulation decision-theoretic rough sets［J］. In ternational Journal of Approximate Reasoning， 2014， 55（1）: 225-237.

［12］ Yang Xi-bei， Qian Yu-hua， and Yang Jing-yu. On characterizing hierarchies of granulation structures via distances［J］. Fundamenta Informaticae， 2013， 123（3）: 365-380.

［13］ M in Fan， Hu Qing-hua， and Zhu W. Feature selection w ith test cost constraint［J］. International Journal of Approximate Reasoning， 2014， 55（1）: 167-179.

［14］ Qian Jin， M iao Duo-qian， Zhang Ze-hua， et al.. Parallel attribute reduction algorithm s using M apReduce［J］. Inform ation Science， 2014， 279（20）: 671-690.

［15］ 陈泽华， 张裕， 谢刚. 基于粒计算的最简决策规则挖掘算法［J］.控制与决策， 2015， 30（1）: 143-148. Chen Ze-hua， Zhang Yu， and Xie Gang. A m ining algorithm for concise decision rules based on granular com puting［J］. Contro l and Decision， 2015， 30（1）: 143-148.

［16］ 陈泽华， 曹长青， 谢刚. 基于粒矩阵的多变量真值表快速约简算法［J］. 模式识别与人工智能， 2013， 26（8）: 745-750. Chen Ze-hua， Cao Chang-qing， and Xie Gang. G ranular matrix based rapid reduction algorithm for multivariab le truth table［J］. Pattern Recognition and Artificial Intelligence，2013， 26（8）: 745-750.

［17］ Chen Ze-hua， Lin T Y， and Xie Gang. Know ledge approximations in binary relation: granular com puting approach［J］. International Journal of Intelligent System， 2013，28（9）: 843-864.

陈泽华： 女，1974年生，副教授，主要研究方向为粒计算、智能信息处理与智能控制.

马 贺： 女，1989年生，硕士生，研究方向为粒计算、组合逻辑优化.

Granu lar M atrix Based Rapid Parallel Reduction A lgorithm for M IMO Truth Table

Chen Ze-hua Ma He
（College of Information Engineering， Taiyuan University of Technology， Taiyuan 030024， China）

Truth table is an im portant tool to represent the logic causal relationships between inputs and outputs. The reduction of the truth tab le is of great significance in analysis and design of digital logic circuit. In this paper，the M IMO tru th tab le is considered as a Logical In form ation System （LIS）， and the traditional tru th table reduction issue is converted into the m inimal ru le discovery of LIS. Granular Com puting （GrC） method is then introduced. Firstly， the logical in formation system is hierarchically granu lated. Secondly， the Granu lar Matrix（GrM） is defined and operated to represent the know ledge in different granularity， together with heuristic in formation hidden in the matrix， the rapid parallel reduction algorithm for the M IMO truth tab le is proposed. Light-Em itting Diode （LED） digital disp lay is app lied to illustrate the com puting process. The mathematical proof and the com p lexity analysis proves the efficiency and valid ity of the p roposed algorithm.

Digital logic circuit； Truth tab le； Granularity； Granu lar M atrix （GrM）； Parallel reduction； Granu lar Com puting （GrC）

TN79； TP181

： A

：1009-5896（2015）05-1260-06

10.11999/JEIT141129

2014-09-01收到，2015-01-16改回

国家自然科学基金（61402319）和山西省回国留学人员科研资助项目（2013-031）资助课题

*通信作者：陈泽华 zehuachen@163.com