岩石结构面粗糙度系数尺寸效应的推拉试验研究

罗战友 ，杜时贵，黄 曼

（1.浙江科技学院 岩土工程研究所，浙江 杭州 310023；2.绍兴文理学院 土木工程学院，浙江 绍兴 312000）

1 引 言

岩体结构面粗糙度系数JRC是影响岩体结构面抗剪强度的关键因素，因此，如何获得结构面粗糙度系数是研究者关注的重点问题[1-6]。

尺寸效应也称尺度效应或比例效应，是指事物的某种特性随研究对象大小不同而变化的现象。基于Barton 的峰值剪切强度破坏准则（JRC-JCS）的结构面粗糙度系数常见的获取方法有3 种：

（1）标准剖面对比法。标准剖面对比法是采用Barton 的10 条标准轮廓曲线来描述JRC 范围为0～20 的具有不同表面形态的结构面，通过实测轮廓曲线与标准轮廓曲线的对比确定JRC 的值，标准剖面对比法的特点是简单、省时，不需要计算，但该法在很大程度上取决于轮廓曲线绘制、测量精度、使用者经验、结构面尺寸等因素[7-10]，因此，精确度较低。而且该方法提供的典型结构面只有单一尺寸（100 mm），无法用于结构面粗糙度系数尺寸效应研究。

（2）理论公式法。该法是通过统计或者分形手段把结构面起伏度、分布及分形特性等代表结构面粗糙起伏特性的参数与结构面粗糙度系数建立函数关系。该方法研究成果较多，常见方法有：表面粗糙度参数法[11-13]、直线与迹线长度比值法[14]、分形理论法[15-16]及直边法[17-18]。虽然理论公式法直接给出了JRC 计算公式，具有简单、方便的优点，较标准剖面对比法更为准确，但该法实质上只是标准剖面法的定量化。除了分形理论及直边法之外，大多理论计算法并不能分析尺寸变化对结构面粗糙度系数的影响。

（3）试验反分析法。该法是通过直剪试验、推拉试验或倾斜试验的测试结果，利用JRC-JCS 准则反算求JRC 值，该方法与岩体赋存状态及节理性状相结合，获得的结构面粗糙度系数最为准确，但由于试验周期长，费用高，往往只在大型或重要工程中采用。在JRC 尺寸效应方面，Barton 等[18]利用不同尺寸原岩张拉结构面的倾斜试验反算出JRC会随着结构面尺寸的增大而减少。Bandis 等[19]通过直剪试验认为，岩体结构面的粗糙度系数也具有尺寸效应。针对结构面而言，常采用100 mm 作为试验室尺寸，且较小结构面是指其尺寸小于300 mm。文中所采用的多尺寸（或多尺度）是根据结构面粗糙度系数的尺寸效应研究要求采用同一尺寸层次范围内的不同试样尺寸，即分别为100、200 mm、…。但由于大尺寸（大于300 mm）原岩结构面获取难度及直剪试验的破坏性，使得结构面粗糙度系数尺寸效应研究受到限制。

综上所述，虽然结构面粗糙度系数的研究成果很多，但针对粗糙度系数尺寸效应的试验研究还很不深入，获得的尺寸效应变化规律也有差异，且数据不全面，难以指导工程实践。由于原岩结构面一般是赋存于岩体中，要想现场多次获得完整原岩结构面是不现实的，而且现场获取的原岩结构面通常是不规则的，易造成原岩结构面上下盘的吻合度差，难以代表真实岩体结构面产状，且成本高，试验周期长[20-21]，因此，模型结构面推拉试验成为结构面粗糙度系数特性研究的重要手段。本文采用研发的结构面制作模具、制备工艺及与天然钙质板岩物理力学特性相类似的岩石模型材料制作了8 组具有不同表面起伏度和粗糙度的结构面，并利用改进的高精度岩石结构面推拉仪开展了8 组结构面粗糙度系数的推拉试验研究，以获得结构面粗糙度系数尺寸效应的变化规律。

2 试件制备及试验装置

2.1 原岩结构面

原岩结构面（见图1）采自浙江省常山县，属于钙质板岩，具有板状结构，是没有重结晶的中性凝灰岩，沿板理方向可以剥成薄片，能获得质量较佳的岩石结构面。选用的结构面微风化、结构致密、坚硬完整，节理面表面光滑～粗糙。图2 是结构面长度为100 mm 岩体结构面的起伏形态。表1为钙质板岩的主要物理力学指标。

图1 天然岩石结构面Fig.1 Images of natural rock joints

图2 天然岩石结构面纵剖线Fig.2 Longitudinal profile of natural rock joint

表1 钙质板岩与模拟岩石的物理力学指标Table 1 Physical and mechanical properties of slate and model rock material

2.2 岩石模型材料

模型材料通常由几种材料混合配制而成，组成模拟材料的原料可分为骨料和胶结材料。常用的骨料有砂（河砂或石英砂）、尾砂、黏土、铁粉、铝粉、云母粉、软木屑、聚苯乙烯颗粒以及硅藻土；胶结材料有熟石膏、水泥、石灰、水玻璃、碳酸钙、石蜡和树脂。在选择岩石结构面的模型材料时，分别对骨料、胶结物及相应的添加剂种类及其合成物的物理力学特性敏感性进行了5 种不同原料配比的无侧限抗压强度和密度试验，根据原岩特性及粗糙结构面的制作要求，选用了中砂（细度模数2.52）、水泥（P·Ⅱ52.5R）、硅粉（920U 微硅粉）、非引气型萘系减水剂（FDN-F2）为模拟岩石的原材料，具体原材料的配合比见表2，获得的模拟岩石物理力学指标见表1，从数值上看，原岩与模拟岩石的性质比较接近。

表2 模型材料配合比Table 2 Mixing ratio of model rock materials

2.3 岩石模型结构面制作模具及工艺

由于岩体结构面的表面形态和上下盘的吻合度是影响结构面抗剪强度参数的关键因素，因此，如果能把原岩结构面表面形态及吻合程度克隆出来就可以代替原岩结构面进行直剪试验。为了解决原岩结构面不能重复取样、上下盘吻合度差、取样困难、工期长、费用高的缺点，研发了能够制作上下盘吻合度高及多尺寸模型结构面的制作模具（见图3），该模具由结构面上盘模具、下盘模具、定位销3 部分构成。

利用岩石结构面试样模具和逆向工程技术，开发了岩石模型结构面的制作工艺，具体制作流程见图4。图5为利用自制模具、模型材料和制作工艺完成的岩石模型结构面上下盘。为了验证原岩和模型结构面的相似度，对4 种不同尺寸的结构面（J1-J8）的起伏幅度均值进行了对比分析，如表3所示。从表中可知：原岩和模型结构面最大起伏幅度的误差范围为1.33%～5.31%，平均值为2.91%；模型结构面上下盘起伏幅度的误差范围为0.07%～2.10%，平均值为1.26%。从数值上看，原岩和模型结构面及其上下盘的吻合程度均很高。

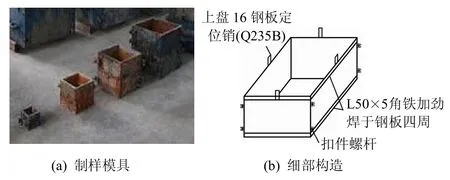
图3 岩石结构面试样模具Fig.3 The designed mold samples for rock joint

图4 岩石模型结构面的制作工艺Fig.4 Production process of rock model joint

图5 岩石模型结构面J1 的上下盘(100、200、300、400 mm)Fig.5 J1 rock model joint(100、200、300、400 mm)

表3 原岩和模型结构面的最大起伏幅度Table 3 Undulation of natural and model rock joints

2.4 岩石结构面推拉试验设备

岩石结构面推拉试验设备是在原有直剪仪的基础上改装而成（见图6），由主机操作台、加载系统、变形测量系统及图像实时显示系统等部分组成，测试的结构面试样尺寸为100～500 mm。该系统采用高精度的负荷传感器，能实现尺寸100～400 mm的结构面推拉试验测试的精度要求。

图6 岩石结构面推拉仪Fig.6 Push-pull shear apparatus of rock joint

3 结构面粗糙度系数的计算方法

JRC是基于Barton 的JRC-JCS 破坏准则[18]提出的，因此，JRC 可通过下式求取：

式中：φp为结构面峰值内摩擦角；JCS为结构面壁岩强度；φr为结构面残余内摩擦角；σn为法向应力。

峰值内摩擦角φp可由推拉试验通过下式获得

式中：τp为峰值剪切强度。

为了通过推拉试验反分析获得结构面粗糙度系数，根据JRC-JCS 准则中相关参数的取值标准和本次试验对未风化或微风化的岩石，可取单轴抗压强度78.1 MPa 作为壁岩强度JCS 值；根据模型材料的直剪试验结果φr取21.8°；为了保证不同试样尺寸（100、200、…、400 mm）具有相同的法向应力条件，采用最大试样尺寸为400 mm 的结构面自重法向应力4.45 kPa 作为试验的法向应力 σn。

4 试验结果及分析

推拉试验选择了8 个原岩结构面作为模板制作了尺寸分别为100、200、300、400 mm 的8 组岩石模型结构面试样，分别记为（J1-100、J1-200、J1-300、J1-400）、…、（J8-100、J8-200、J8-300、J8-400）。为了避免试验偶然误差影响，对同一结构面采用多次重复试验方法进行试验数据统计处理，图5为J1 结构面在尺寸分别为100、200、…、400 mm的6 次重复试验强度，由图可知，在同一尺寸下，重复试验次数对结构面测试结果影响较小，这是因为试验采用的法向荷载（4.45 kPa）相对于结构面壁岩强度（78.1 MPa）较小，故在此法向荷载下推拉试验对表面磨损程度极其微小，因此，本文采用单试件法进行多次重复试验。在试验过程中，为了保证同一试样多次重复试验的可比性，在试样外侧不同位置采用多条等间距刻度线措施保证结构面试样上下盘的吻合度。

图7 J1 结构面不同尺寸的6 次重复试验强度Fig.7 Six times repeatedly testing strength of different sizes of joint J1

4.1 结构面粗糙度系数的尺寸效应试验研究

图8为8 组模型结构面（J1、J2、…、J8）的粗糙度系数随结构面尺寸的变化规律，图9为8 组模型结构面的粗糙度系数统计均值随结构面尺寸的变化规律。从图中可知：①8 组模型结构面粗糙度系数随尺寸的变化规律不尽相同，结构面J2、J3、J4、J5、J7 的粗糙度系数呈现出随结构面尺寸的增加而降低趋势；结构面J1、J8 的粗糙度系数不随试样尺寸的变化而变化，基本上保持一定值；结构面J6 的粗糙度系数随尺寸增加呈现出先减少后增大的趋势；②从8 个结构面统计均值来看，粗糙度系数随试样尺寸的增大而降低，基本上呈现出负指数的变化规律。③不同结构面在相同法向应力下的粗糙度系数也有差异，主要原因是由于8 个原岩结构面具有不同的起伏和粗糙程度造成的。

图8 J1～J8 结构面粗糙度系数随尺寸的变化规律Fig.8 Variations between rock roughness coefficient and the size

4.2 与结构面粗糙度系数理论公式的对比

Barton[22]根据200 多组结构面的粗糙度系数与表面参数的相关性分析结果认为，结构面表面轮廓线的相对起伏幅度（Ry/Ln）与粗糙度系数JRC 有良好相关性，并在此基础上提出了JRC 测量的直边法公式为

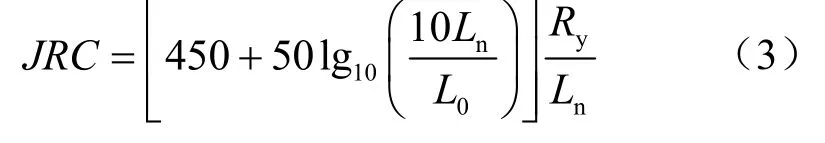
式中：Ry为凸起体起伏度值（cm）；L0为试验室结构面轮廓曲线长度（cm）；Ln为结构面轮廓曲线长度（cm）。

图9 J1～J8 结构面粗糙度系数统计均值Fig.9 Statistical mean joint roughness coefficient

图10 是采用Barton 公式计算出结构面粗糙度系数随试样尺寸的变化规律，从图中可知，对于8组结构面，理论公式计算的粗糙度系数均随结构面试样尺寸的增大而降低，呈现出负指数的变化规律，这与粗糙度系数尺寸效应的试验值变化趋势不完全一致。

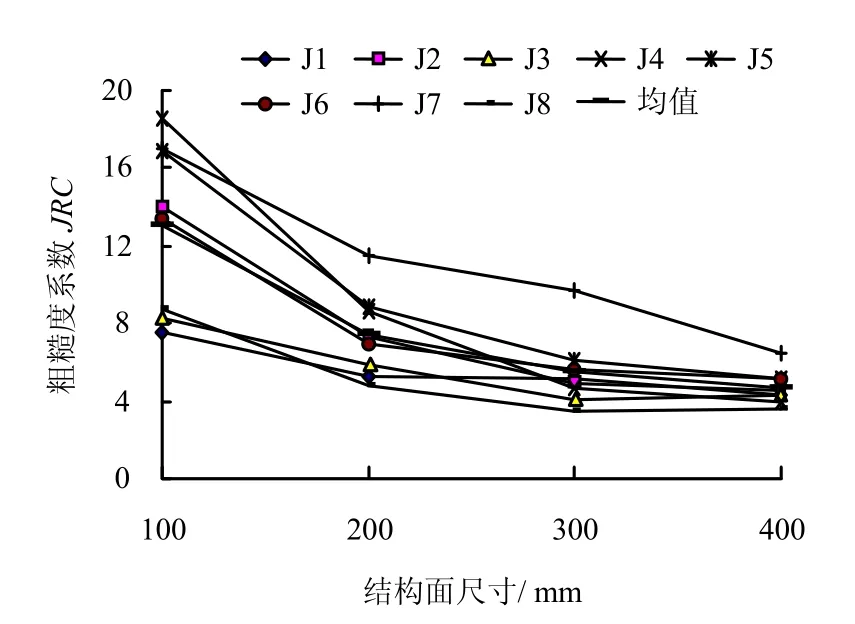
图10 粗糙度系数（Barton 公式）随尺寸的变化规律Fig.10 Variations between Barton theoretical value and size

图11 是粗糙度系数试验统计均值与Barton 理论公式计算均值对比，由图可知，虽然结构面粗糙度系数的试验与理论统计均值均呈现出随试样尺寸增大而降低的变化规律，但理论值变化幅度明显高于试验值，且结构面尺寸越小，试验值与理论值差别越大，最大偏差可达到110%。

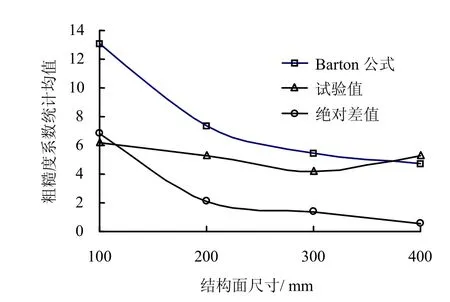
图11 粗糙度系数试验值与Barton 理论公式的对比Fig.11 Comparison between testing values and these calculated by Barton formula of joint roughness coefficient

5 讨 论

5.1 表面形貌对粗糙度系数尺寸效应的影响

由前述试验测试结果可知，8 组结构面粗糙度系数尺寸效应试验变化规律不尽相同，根据对8 组结构面表面形貌分析表明：①对于粗糙度系数尺寸效应呈现出递减变化趋势的结构面（J2、J3、J4、J5、J7），其表面形貌整体上呈现出随尺寸增大其相对起伏幅度也在增大；②对于粗糙度系数尺寸效应几乎没有变化的结构面（J1、J8），其表面形貌整体上分布比较均匀，且在最小测试尺寸范围内（100 mm）相对起伏幅度变化不大；③对于粗糙度系数尺寸效应呈现出先减少后增大趋势的结构面（J6），其表面形貌表现为两端部的相对起伏幅度较结构面内部的相对起伏幅度大。因此，结构面的粗糙度系数尺寸效应并不是总是随试样尺寸的增大而减小，而是与结构面表面形貌分布相关。

5.2 起伏幅度对结构面粗糙度系数影响评价

研究表明，起伏幅度 Ry或者相对起伏幅度 Ry/Ln是结构面粗糙度系数的重要影响因素。Barton 采用相对起伏幅度给出了粗糙度系数的尺寸效应评价公式与试验值结果相差较大，且尺寸越小，相差就越大，主要原因是结构面粗糙度系数除了与相对起伏幅度值有关外，其分布形态（三维分布和剖面间距）也是影响粗糙度系数JRC 的重要因素，大尺寸结构面较小尺寸结构面的分布形态更趋于稳定。因此，大尺寸结构面粗糙度系数理论计算取值相对较为精确。

6 结 论

（1）采用中砂、水泥、硅粉、非引气型萘系减水剂等原材料制作的模型结构面试样，其三维表面形貌与原岩结构面的表面形态近似一致，可利用模型结构面来代替原岩结构面进行粗糙度系数测试。

（2）模型结构面粗糙度系数的统计均值随试样尺寸的增加而降低，但特定结构面粗糙度系数的尺寸效应规律需要根据结构面的具体表面形貌进行测试。因此，在工程中粗糙度系数需要根据表面形貌和分布特征进行综合判定。

（3）Barton 理论公式计算的结构面粗糙度系数尺寸效应变化规律与推拉试验测试规律总体上一致，但试验值与理论值有差异，且结构面试样尺寸越小，二者差异就越大。

（4）由于结构面表面起伏粗糙程度不同，造成具有特定表面形貌的模型岩石结构面粗糙度系数也有差异。

[1]BARTON N.Review of a new shear strength criterion for rock joints[J].Engineering Geology,1973,7:287-332.

[2]夏才初,孙宗硕,潘长良.不同形貌节理的剪切强度和闭合变形研究[J].水利学报,1996,(11):28-32,38.XIA Cai-chu,SUN Zong-suo,PAN Chang-liang.Study on shear strength and closure deformation of different morphologies joints[J].Journal of Hydraulic Engineering,1996,(11):28-32,38.

[3]ZHAO J.Joint surface matching and shear strength.Part A:joint matching coefficient(JMC)[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(2):173-178.

[4]GRASSELLI G.Shear strength of rock joints based on quantified surface description[J].Rock Mechanics and Rock Engineering,2006,39(4):295-314.

[5]UENG TZOU-SHIN,JOU YUE-JAN,PENG I-HUI.Scale effect on shear strength of computer-aidedmanufactured joints[J].Journal of GeoEngineering,2010,5(2):29-37.

[6]BARTON N.Shear strength criteria for rock,rock joints,rockfill and rock masses:Problems and some solutions[J].Journal of Rock Mechanics and Geotechnical Engineering,2013,5(4):249-261.

[7]MILLER S M,MCWILLIAMS P C,KERKERING J C.Ambiguities in estimating fractal dimensions of rock fracture surfaces[C]//Proceeding of the 31st U.S.Symposium on Rock Mechanics.Rotterdam:[s.n.],1990:471-478.

[8]HSIUNG S M,GHOSH A,AHOLA M P,et al.Assessment of conventional methodologies for joint roughness coefficient determination[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1993,30:825-829.

[9]HONG E S,LEE J S,LEE I M.Underestimation of roughness in rough rock joints[J].International Journal of Numerical and Analytical Methods in Geomechanics,2008,32(11):1385-1403.

[10]GE Y,KULATILAKE PHSW,TANG H,et al.Investigation of natural rock joint roughness[J].Computers and Geotechnics,2014,5:290-305.

[11]TSE R,CRUDEN D M.Estimating joint roughness coefficients[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1979,16(5):303-307.

[12]FARDIN N,STEPHANSSON O,JING L.The scale dependence of rock joint surface roughness[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,2001,38:659-669.

[13]FENG Q,FARDIN N,JING L,et al.A new method for in situ non-contact roughness measurement of large rock fracture surfaces[J].Rock Mechanics and Rock Engineering,2003,36:3-25.

[14]MAERZ N H,FRANKLIN J A,BENNETT C P.Joint roughness measurement using shadow profilometry[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1990,27:329-343.

[15]LEE Y H,CARR J R,BARR D J,et al.The fractal dimension as a measure of the roughness of rock discontinuity profiles[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1990,27(6):453-464.

[16]XIE H P,WANG J A,XIE W H.Fractal effects of surface roughness on the mechanical behavior of rock joints[J].Chaos,Solitons and Fractals,1997,8(2):221-252.

[17]DU Shi-gui,HU Yun-jin,HU Xiao-fei.Measurement of joint roughness coefficient by using profilograph and roughness ruler[J].Journal of Earth Science,2009,20(5):890-896.

[18]BARTON N,CHOUBEY V.The shear strength of rock joints in theory and practice[J].Rock Mechanics and Rock Engineering,1977,10(1):1-54.

[19]BANDIS S,LUMSDEN A C,BARTON N.Experimental studies of scales effects on the shear behaviour of rock joints[J].International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts,1981,18(1):1-21.

[20]杜时贵,黄曼,罗战友,等.岩石结构面力学原型试验相似材料研究[J].岩石力学与工程学报,2010,29(11):2263-2270.DU Shi-gui,HUANG Man,LUO Zhan-you,et al.Similar material study of mechanical prototype test of rock structural plane[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(11):2263-2270.

[21]黄曼,罗战友,杜时贵,等.系列尺度岩石结构面相似表面模型制作的逆向控制技术研究[J].岩土力学,2013,34(4):1211-1216.HUANG Man,LUO Zhan-you,DU Shi-gui,et al.Study of inverse controlling technology for series scales similar surface model making of rock structural plane[J].Rock and Soil Mechanics,2013,34(4):1211-1216.

[22]BARTON N,BANDIS S.Review of predictive capability of JRC-JCS model in engineering practice[M]//Rock Joints.[S.l.]:Balkema A A.,1990:603-610.