多连梁剪力墙抗震性能研究

范重+刘畅+吴徽

摘要：针对剪力墙结构设计中容易出现连梁剪压比不足的问题，提出多连梁的设计理念，通过设置多个连梁代替传统单连梁的方式，可以有效增大连梁的抗剪面积与跨高比，明显改善结构的抗震性能。确定多连梁截面尺寸的基本原则是结构的侧向刚度与单连梁保持不变。对剪力墙结构在多遇地震作用下进行了详细分析，全面比较了多连梁与单连梁对结构动力特性、层间位移角、侧向刚度和构件内力的影响以及对改善连梁剪压比的作用。对剪力墙结构进行了在罕遇地震作用下的弹塑性时程分析，研究了多连梁剪力墙结构对最大层间位移角、塑性铰分布、抗剪承载能力及结构非线性耗能能力的改善效果；采用非线性有限元法对连梁在往复地震作用下的抗震性能进行研究。结果表明：由于多连梁跨高比大，其破坏形态从剪切破坏转化为弯曲破坏，构件的延性显著增大。

关键词：超高层建筑；剪力墙；连梁；刚度；抗剪承载力；延性；耗能能力

中图分类号：TU398.2 文献标志码：A

0 引 言

剪力墙是在高层与超高层建筑设计中采用的最为广泛的结构形式，剪力墙作为结构主要承重构件的同时，还是最主要的抗侧力结构。

为了避免剪力墙墙肢过长形成低矮墙以及小剪跨比造成的墙体延性降低，当墙体长度大于8 m时，可以通过建筑门洞或设置结构洞口的方式，形成联肢剪力墙结构。剪力墙结构通过连梁将各墙肢连接在一起，使得各墙肢协调变形，形成整体抗侧力结构，从而可以抵抗地震作用与风荷载的水平剪力与倾覆力矩。因此，连梁对于保证剪力墙结构的抗震性能至关重要。

迄今为止，各国学者对剪力墙结构特别是连梁的抗震性能进行了大量研究工作。Paulay等[1]针对小跨高比连梁抗震设计中存在的问题，提出了交叉布置对角斜筋的方式。Tegos等[2]提出了菱形配筋方案，试验结果表明，菱形配筋能够有效防止连梁发生突发性劈裂破坏。龚炳年等[3]通过36根连梁试验，得出了对于小跨高比连梁即使在较低名义剪压比时位移延性仍然较小的结论。范重等[4-5]在对各国剪力墙结构发展历程进行全面回顾的基础上，对超高层建筑剪力墙设计中需要注意的关键技术问题进行了讨论，并采用数值方法对不同配筋形式小跨高比连梁的受力性能进行了分析。王崇昌等[6]通过2个带有水平通缝的连梁试验，提出当跨高比小于1.5时，通过在连梁中设置水平通缝的方法可以防止连梁发生剪切破坏，提高连梁延性。李奎明等[7]提出了高性能混凝土双连梁短肢剪力墙的新形式，对构件初始刚度、承载力和延性的试验结果表明，该结构具有良好的抗震性能。郭猛等[8]运用程序SATWE和ETABS对双连梁结构进行了数值模拟，结果表明双连梁在降低连梁刚度的同时，对连梁的耗能能力影响不大。

跨高比是影响连梁抗震性能的主要因素，当连梁的跨高比很小时，连梁承受的剪力很大，梁端弯矩相对很小，连梁的变形能力与耗能均较小，构件发生剪切破坏，无法实现“强剪弱弯”的塑性变形机制。随着跨高比增加，连梁的抗震延性逐渐改善。此外，连梁的抗剪承载力对其抗震性能的影响非常突出。《高层建筑混凝土结构技术规程》（JGJ 3—2010）[9]中规定连梁抗剪截面验算时以跨高比2.5为界限，当跨高比小于2.5时，连梁抗剪承载力需要相应降低。在实际工程中，由于连梁与墙肢相比截面尺寸相差悬殊，而且连梁部位的变形非常集中，连梁中的弯矩和剪力均很大，连梁抗剪截面不足，无法满足规范要求的情况比较突出。采取降低连梁高度和对连梁刚度进行折减等措施虽然可以减小连梁的内力，但同时会降低结构的整体侧向刚度。

为了在保证结构侧向刚度的前提下改善剪力墙结构的抗震性能，本文提出一种适用于结构洞口的多连梁剪力墙，包括双连梁与三连梁等形式。通过在同一楼层沿高度设置多个连梁的方式，减小单个连梁的截面高度，增加其跨高比与抗剪面积。给出多连梁截面尺寸的计算方法，使得多连梁与传统单连梁结构侧向刚度保持不变。通过典型结构算例，对剪力墙在多遇地震作用下的抗震性能进行系统分析，比较多连梁与单连梁对结构动力特性、层间位移角、侧向刚度和构件内力的影响以及对改善连梁剪压比的作用。采用非线性有限元法对连梁在往复地震作用下的抗震性能进行分析，研究跨高比对连梁破坏形态与延性的影响，得到连梁的滞回曲线和骨架曲线。对剪力墙结构进行了在罕遇地震作用下的弹塑性时程分析，研究了多连梁剪力墙结构对最大层间位移角、塑性铰分布、抗剪承载力以及结构非线性耗能能力的改善效果。

1 多连梁剪力墙结构

1.1 结构形式

为了保证剪力墙的延性，需要避免结构中的墙肢过长形成低矮剪力墙，通常采用在剪力墙设置结构洞口的方式。由于超高层建筑需要具有足够的侧向刚度，因此墙体开洞后，连梁的截面高度不能太小。为了避免小高宽比连梁抗震性能降低的问题，本文提出一种适用于长墙肢结构洞口的新型连梁形式，即在每个结构楼层沿高度均匀布置多个连梁取代传统的单连梁。单连梁、双连梁和三连梁的形式如图1所示，其中，h1，h2，h3均为截面高度。

当多连梁的抗弯刚度之和与单连梁的抗弯刚度相等时，剪力墙结构的侧向刚度可以基本保持不变，对整体结构的力学特性影响不大。进行上述刚度等效后，多连梁中各连梁的截面高度小于单连梁，但其面积之和显著大于单连梁，使得连梁的抗剪能力大幅提高。随着连梁截面高度减小，连梁的跨高比随之增大，将显著改善连梁的延性与耗能能力，有利于实现“强墙肢、弱连梁”的抗震设计理念。

1.2 连梁刚度的确定方法

在进行多连梁剪力墙结构设计时，采用多连梁与单连梁抗弯刚度等效的方法，应按下式进行计算

1为单连梁的截面惯性矩；Ii为多连梁的截面惯性矩，i为多连梁的根数，i=2，3，…。

由于连梁的跨高比通常较小，需要考虑剪切变形的影响。为了简单起见，假定在水平荷载作用下连梁两端的转角相等。此时，连梁端部弯矩M与转角θ的关系可由下式确定endprint

式中：EI为连梁抗弯刚度；G为连梁剪切模量；A为连梁截面面积；h为连梁高度；ln为连梁的跨度；β为剪切变形系数；k为剪力不均匀系数，对于矩形截面连梁，k=1.2。

由连梁端部的弯矩可得到连梁的剪力V为

当连梁总刚度一定时，在水平荷载作用下墙肢的转角沿高度基本保持不变，假定此时多连梁的梁端弯矩与单连梁的梁端弯矩相等，由式（1）可得

由于连梁宽度保持不变，多连梁时各连梁截面高度与单连梁高度的关系如下

（6）2 多连梁剪力墙结构的弹性分析

2.1 计算模型

为了深入研究多连梁的结构性能，避免其他因素的影响，本文中选取具有代表性的15层剪力墙作为研究对象，如图2所示。模型中剪力墙墙肢长度为8 m，两端带有2.8 m长的翼墙，楼层高度均为4.2 m。在墙肢中部设有洞口，连梁高度为800 mm。根据上述确定多连梁高度的方法，得到单连梁、双连梁、三连梁的截面尺寸及其相应的跨高比，结果如表1所示。

在计算结构自重时，假定楼板厚度为120 mm。为了模拟结构的重力荷载代表值，在各层的墙肢上施加线荷载，其中恒载为80 kN·m-1，活载为65 kN·m-1，墙肢底部在重力荷载作用下的轴压比约

为0.40。抗震设防烈度为8度，Ⅲ类场地。混凝土强度等级为C40，钢筋均为HRB400。

采用PMSAP软件进行结构弹性抗震计算，仅考虑结构平面内的受力状态。采用振型分解反应谱法进行弹性分析，连梁的刚度折减系数取0.7。

多连梁模型除连梁截面高度外，均与单连梁模型一致。

2.2 弹性分析的计算结果

为了考察多连梁剪力墙的性能，分别对单连梁、双连梁和三连梁剪力墙进行了计算分析。多连梁与单连梁剪力墙结构的自振周期以及在地震作用下的侧向位移如表2所示。从表2可以看出，单连梁结构的第1自振周期为1.542 s，相应的振型质量参与系数为68.4%，最大层间位移角为1/1 075。双连梁与三连梁结构的第1自振周期都较单连梁小，两者与单连梁的差异分别为2.32%与2.87%。双连梁与三连梁结构的顶点位移均比单连梁小，两者与单连梁的差异分别为1.92%与2.71%。双连梁与三连梁结构的最大层间位移角均比单连梁小，两者与单连梁的差异分别为1.40%与3.53%。结果表明，多连梁模型与单连梁模型在结构性能方面基本保持一致。

为了考察多连梁对剪力墙结构侧向刚度的影响，采用楼层剪力V除以层间位移Δu的算法得到楼层的侧向刚度，结果如表3所示。从表3可以看出，除底层数层和顶层外，双连梁结构楼层的侧向刚度与单连梁差异在5%以内，三连梁与单连梁差异在9%以内。底部楼层位移绝对值较小，因此其的相对误差较大。

多连梁与单连梁在地震作用下的梁端弯矩和剪力如表4所示。为了避免内力调整等因素的影响，表4中仅考虑地震单工况时连梁的内力。从表4可以看出，除顶层与底层的差异较大外，双连梁与单连梁的梁端弯矩和剪力差异较小，平均差异不大于4%，三连梁与单连梁的梁端弯矩和剪力的平均差异为7%～9%。上述结果表明，根据连梁抗弯刚度等效确定多连梁的高度，对连梁内力的影响较小。

根据《高层建筑混凝土结构技术规程》（JGJ 3—2010）[9]的规定，在地震工况时，连梁的抗剪承载力（剪压比）与其跨高比有关，当跨高比大于2.5时，剪压比限值为0.20；当跨高比不大于2.5时，剪压比限值为0.15。由此可见，跨高比较大的连梁，其截面抗剪承载力较高。多连梁与单连梁剪力墙在地震作用下的剪压比如表5所示。从表5可以看出，对于单连梁结构，各层连梁的平均剪压比与剪压比限值之比为0.9，其中结构下部2～7层连梁的剪力已经超过承载力限值。对于双连梁模型，各层连梁的平均剪压比与剪压比限值之比为0.41，连梁剪力均无超限情况。对于三连梁模型，各层连梁的平均剪压比与剪压比限值之比进一步减小为0.36，无连梁剪力超过限值情况发生。由此可见，在进行超高层建筑抗震设计时，多连梁方式对于控制截面剪压比和提高抗震性能作用非常显著。

3 连梁跨高比对抗震性能的影响

在对连梁进行弹塑性有限元分析时采用MARC软件，计算模型中混凝土采用三维实体单元，钢筋采用线单元，按照连梁的实际配筋形式进行建模，单元几何属性按照实际钢筋面积赋值。钢筋与混凝土采用MARC软件中的Insert功能进行耦合，不考虑钢筋与混凝土之间的粘结滑移。有限元模拟的边界条件与连梁试验[10]类似，采用连梁反弯点加载。将连梁左端设定为固定边界条件，采用耦合功能将连梁右端的所有节点自由度凝聚到一个节点上，保证该面不发生转动，相当于在连梁的右端设置滑动支座，利用变形量进行加载。

为了验证弹塑性计算参数的准确性，与连梁的试验结果进行了对比。根据文献[11]中连梁的试验数据，对其中试件SB-2和CB-2进行有限元模拟分析，与试验结果吻合良好。

根据上述多连梁在多遇地震作用下的弹性计算，可以得到单根连梁的弯矩与剪力，按照现行结构设计规范中的方法，分别确定连梁的纵筋与箍筋，如表6与图3所示。

连梁在往复荷载作用下的滞回曲线如图4所示，其中，Δ为位移。从图4可以看出：单连梁的滞回曲线存在一定程度的捏拢现象，承载力下降较快；多连梁的滞回曲线相对饱满，耗能能力增加，说明多连梁的抗震性能优于单连梁。

多连梁与单连梁骨架曲线的对比如图5所示。

从图5可以看出，多连梁与单连梁在往复荷载作用下的骨架曲线基本重合，说明各连梁的初始刚度比较接近，承载能力基本相同。对于单连梁模型，在连梁达到最大承载力后，变形的发展能力较低，连梁承载能力下降很快。与此相对应，多连梁模型的骨

图5 多连梁与单连梁的骨架曲线对比

Fig.5 Comparisons of Skeleton Curves Betweenendprint

Multi-coupling Beams and Single Beam架曲线均具有明显的水平段，连梁在达到最大承载能力后能够维持较好的变形能力，说明多连梁的延性得到明显提高。

不同连梁模型的抗弯承载力、变形和延性系数如表7所示。从表7可以看出，3种连梁模型的开裂荷载、屈服荷载、最大荷载及其相应的变形均比较接近，但双连梁的延性系数比单连梁提高33.5%，三连梁的延性系数比单连梁提高59.8%。单连梁相应的最大层间位移角为1/68，双连梁与三连梁的最大层间位移角分别为1/50和1/45，可见多连梁对于改善构件变形能力作用显著。4 多连梁剪力墙结构的弹塑性分析

4.1 材料本构关系与计算模型

为了研究多剪力墙结构在罕遇地震作用下的抗震性能，采用PERFORM-3D软件进行对如图2所示的剪力墙结构进行弹塑性分析。

将结构墙体中的混凝土分为约束区和非约束区，在剪力墙暗柱范围均采用约束区混凝土的本构关系，在其他部位采用非约束区混凝土的本构关系。约束区混凝土本构关系采用Mander等[12]的模型，非约束区混凝土本构关系采用《混凝土结构设计规范》（GB 50010—2010）[13]中混凝土材料的受压曲线，忽略混凝土的受拉强度，假定拉力全部由钢筋承担。非约束区与约束区C40混凝土的本构关系曲线如图6所示，其中，f为应力，ε为应变。

混凝土的恢复力模型如图7所示。采用纤维骨架模型，卸载刚度等于初始刚度。剪力墙中钢筋均为HRB400，采用三折线模型，钢筋的应力-应变曲线如图8所示，其中，fy，fu分别为钢材的屈服强度和最大强度，εy，εy1，εu分别为钢材的屈服应变、最大强度相应的应变和极限应变。

中的剪力墙单元（纤维模型）模拟剪力墙的压弯受力性能，其非线性性能以及耗能能力由剪力墙的钢筋和混凝土的材料非线性性能和滞回性能决定。假定剪力墙平面内的剪切变形为非线性[14]，并设置剪切变形监测单元，以检验剪力墙的剪压比。剪力墙平面外的弯曲、剪切均为弹性。剪力墙配筋采用多遇地震作用下弹性分析的计算结果，边缘构件的配筋率为0.8%，墙体分布钢筋的配筋率为0.5%。

从上述连梁的滞回性能分析得到连梁的骨架曲线，从而可以定义PERFORM-3D计算模型中力-位移关系曲线[15]的广义力和广义位移。连梁采用梁单元进行模拟，在连梁两端设置集中塑性铰，并且在连梁中部设置剪切铰，用于判断连梁的剪力是否超过限值。在结构弹塑性时程分析时考虑荷载-位移效应的影响。

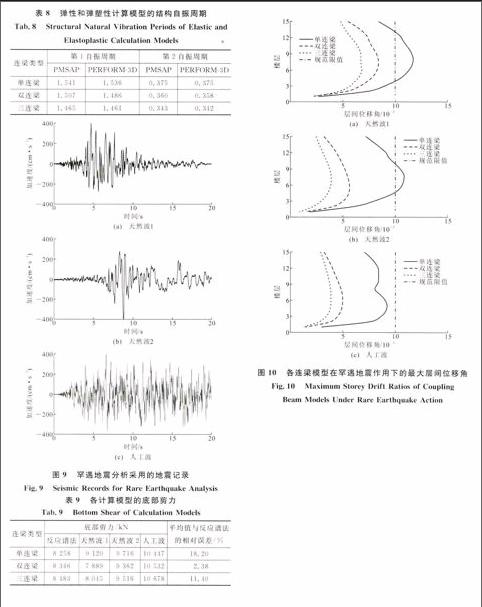
为保证弹塑性模型的正确性，对弹塑性模型PERFORM-3D与弹性模型PMSAP的动力特性进行了对比，如表8所示。从表8可以看出，各连梁模型的结构自振周期吻合很好，结构总质量保持一致，弹塑性模型能够准确反映结构的弹性动力特性。

在进行弹塑性分析时，选用2条天然波与1条人工波（图9），各计算模型在弹性分析时的底部剪力如表9所示。从表9可以看出，天然波与人工波计算得到的底部剪力均与反应谱法比较接近。

4.2 弹塑性分析结果

4.2.1 最大层间位移角

各连梁模型在罕遇地震作用下的最大层间位移角如图10所示。从图10可以看出，单连梁结构的

最大层间位移角为1/86，2条天然波的结构层间位移角均超过了1/100的抗震性能目标，过大的层间位移角引起了结构破坏。人工波时相当多楼层的最大层间位移角也接近了1/100。由于单连梁的变形超过其极限变形能力，计算至10 s左右时终止，3条地震波均没有达到其时程波的长度。

在3条地震波的作用下，双连梁结构的最大层间位移角为1/134，三连梁结构的最大层间位移角为1/141，均可满足最大层间位移角不大于1/100的限值，明显小于单连梁时的情况，说明多连梁对于避免结构发生严重破坏和减小结构的最大层间位移角起到显著作用。

4.2.2 连梁的抗剪承载力

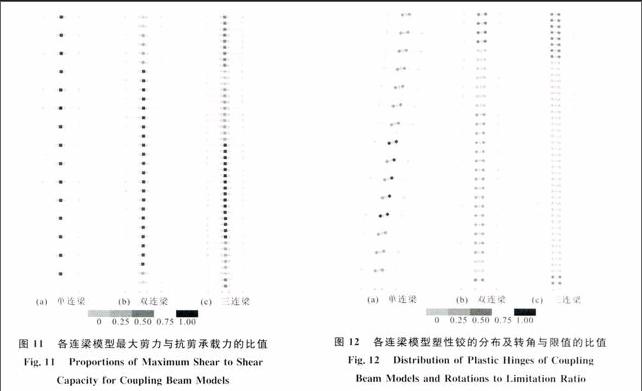
在各计算模型中，与最大层间位移角相对应，连梁的最大剪力与抗剪承载力的比值如图11所示。从图11可以看出，在单连梁模型中，所有连梁的剪力都超过了连梁的极限抗剪承载力。对于双连梁模型，顶部和底部部分楼层的连梁尚未达到连梁的极限抗剪承载力。对于三连梁模型，在底部和顶部有更多的连梁剪力较小，尚有较大的强度储备。

4.2.3 梁端塑性铰与耗能性能

在罕遇地震作用下，各连梁模型在达到地震加速度峰值以前，连梁均已出现塑性铰而进入塑性。塑性铰首先出现在结构中下部4～6层范围内的连梁，随着时间推移，塑性铰屈服逐渐向结构上部发展，最后所有楼层连梁均进入屈服。

单连梁模型部分连梁的端部转角存在大于1/50限值的情况，未能达到结构的抗震性能目标。双连梁模型的梁端转角需求和转动能力之比较小，且分布比较均匀。三连梁模型所有连梁的梁端转角需求和转动能力之比进一步减小，塑性铰分布也更加均匀。这说明多连梁结构比单连梁结构的抗震性能明显改善。各连梁模型的塑性铰分布及转角与限值的比值如图12所示。

4.2.4 连梁的耗能能力

各连梁模型在8 s左右连梁开始屈服，结构的塑性耗能能力开始增加，此时耗散能量占总能量的15%。在15 s左右所有连梁均屈服，结构的塑性耗能进一步增加，此时结构的塑性耗能占总能量的30%，随后结构的塑性耗能稳定在40%左右，由于普通连梁模型的连梁转动能力较低，延性较差，计算到13 s时终止，结构的塑性耗能并没用充分发展，结构的耗能能力很差，这也与前面的层间位移以及连梁的抗剪需求能力比以及连梁塑性铰的需求能力比相对应。双连梁和三连梁的耗能能力比较接近，最终稳定在35%左右。

结构中的非线性耗能基本上全部为连梁耗散的地震能力，墙肢的非线性耗能占总能量的比例不超过5%。基本可以认为剪力墙墙肢破坏程度较小，连梁充分发挥了抗震设防的第1道防线作用，通过连梁梁端塑性铰的能量耗散，保护了墙肢在地震作用下免遭严重破坏。5 结 语endprint

（1）在剪力墙结构中，连梁抗剪截面不足和构件变形能力较差的问题突出，是导致连梁超筋的关键。

（2）在同一楼层采用多个连梁代替单连梁，可以有效增大连梁的抗剪面积，极大地提高了连梁的抗剪能力。

（3）多连梁剪力墙结构中，单根连梁的跨高比增大，构件变形能力增强，可以明显改善构件的延性。

（4）本文提出了确定多连梁截面尺寸的抗弯刚度等效方法，剪力墙结构在弹性阶段的动力特性、层间位移角、侧向刚度等性能基本保持不变。

（5）剪力墙结构在罕遇地震作用下的弹塑性时程分析结果表明，多连梁剪力墙结构对最大层间位移角、塑性铰分布、抗剪承载力以及结构非线性耗能能力等方面的改善均显著优于传统的单连梁剪力墙结构。

（6）多连梁的抗震性能显著优于传统的单连梁，三连梁的抗震性能优于双连梁。

（7）多连梁作为解决剪力墙结构超筋问题的有效手段，具有良好的应用前景。

致谢：在本文的完成过程中，得到了清华大学钱稼茹教授与赵作周教授的指导与帮助，在此谨致以衷心的感谢！

参考文献：

References：

[1] PAULAY T，BINNEY J R.Diagonally Reinforced Coupling Beams of Shear Walls[J].ACI Special Publication，1974，42（2）：579-598.

[2]TEGOS I A，PENELIS G G.Seismic Resistance of Short Columns and Coupling Beams Reinforced with Inclined Bars[J].ACI Structural Journal，1998，85（1）：82-88.

[3]龚炳年，方鄂华.反复荷载下联肢剪力墙结构连梁的性能[J].建筑结构学报，1988，9（1）：34-41.

GONG Bing-nian，FANG E-hua.Behavior of Reinforced Concrete Coupling Beams Between Shear Walls Under Cyclic Loading[J].Journal of Building Structures，1988，9（1）：34-41.

[4]范 重，刘学林，黄彦军.超高层建筑剪力墙设计与研究的最新进展[J].建筑结构，2011，41（4）：33-43.

FAN Zhong，LIU Xue-lin，HUANG Yan-jun.The Up to Date Development on Design and Research of Shear Wall in High-rise Buildings[J].Building Structure，2011，41（4）：33-43.

[5]范 重，李 波，范学伟.超高层建筑剪力墙短连梁有效配筋形式研究[J].建筑结构，2009，39（增1）：496-499.

FAN Zhong，LI Bo，FAN Xue-wei.Research on Effective Reinforcement Arrangement of Coupling Beam with Small Aspect Ratio in Shear Walls of Super-tall Building[J].Building Structure，2009，39（S1）：496-499.

[6]王崇昌，王宗哲，陈 平，等.钢筋混凝土剪力墙的延性[J].西安建筑科技大学学报：自然科学版，1987，19（1）：15-24.

WANG Chong-chang，WANG Zong-zhe，CHEN Ping，et al.Ductility of Reinforced Concrete Shear Walls[J].Journal of Xian University of Architecture & Technology：Natural Science Edition，1987，19（1）：15-24.

[7]李奎明，孙春毅，李 杰.高性能混凝土双连梁短肢剪力墙试验研究[J].地震工程与工程振动，2006，26（3）：121-123.

LI Kui-ming，SUN Chun-yi，LI Jie.Experimental Study on HPC Short-leg Shear Wall with a Pair of Beams[J].Earthquake Engineering and Engineering Vibration，2006，26（3）：121-123.

[8]郭 猛，姚谦峰，刘 佩.框架-核心筒结构剪力墙连梁设计[J].华中科技大学学报：自然科学版，2009，37（5）：102-105.

GUO Meng，YAO Qian-feng，LIU Pei.Design of Shear-wall Coupling Beams in Frame-core Wall Structure[J].Journal of Huazhong University of Science and Technology：Natural Science Edition，2009，37（5）：102-105.

[9]JGJ 3—2010，高层建筑混凝土结构技术规程[S].

JGJ 3—2010，Technical Specification for Concret Structures of Tall Building[S].endprint

[10]张 涛.小跨高比连梁抗震性能试验研究与分析[D].西安：西安建筑科技大学，2008.

ZHANG Tao.Theoretical Analysis and Experimental Study on Coupling Beam with Small Span-to-depth Ratio[D].Xian：Xian University of Architecture and Technology，2008.

[11]梁启智，韩小雷.低周反复荷载作用下刚性连梁及普通连梁性能[J].华南理工大学学报：自然科学版，1995，23（1）：27-33.

LIANG Qi-zhi，HAN Xiao-lei.The Behavior of Stiffening Beams and Lintel Beams Under Cyclic Loading[J].Journal of South China University of Technology：Natural Science，1995，23（1）：27-33.

[12]MANDER J B，PRIESTLEY M J N，PARK R.Theoretical Stress-strain Model for Confined Concrete[J].Journal of Structural Engineering，1988，114（8）：1804-1826.

[13]GB 50010—2010，混凝土结构设计规范[S].

GB 50010—2010，Code for Design of Concrete Structures[S].

[14]王晓楠，苗启松，吴 徽.基于宏观模型的剪力墙静力弹塑性分析[J].建筑结构，2011，41（增1）：260-263.

WANG Xiao-nan，MIAO Qi-song，WU Hui.Static Pushover Analysis of Shear Wall Based on Macro Model[J].Building Structure，2011，41（S1）：260-263.

[15] Computer and Structure Inc.Perform-3D Components and Elements[M].Berkeley：Computer and Structure Inc，2011.endprint