单框架控制力矩陀螺部分失效时的空间站姿态机动方法*

赵　乾，唐国金

(国防科技大学 航天科学与工程学院， 湖南 长沙　410073)



单框架控制力矩陀螺部分失效时的空间站姿态机动方法*

赵乾，唐国金

(国防科技大学 航天科学与工程学院， 湖南 长沙410073)

摘要：对金字塔构型单框架控制力矩陀螺(SGCMG)的失效特性进行分析。结合SGCMG部分失效的特点，构建运用Legendre伪谱法的重规划姿态机动路径求解方法。考虑SGCMG失效情况的不可预测性，设计自适应操纵律，该操纵律可以根据指令力矩与输出力矩的偏差对SGCMG的失效情况进行诊断，从而调节操纵律的内部参数，实现失效情况操纵律的自适应调节。仿真结果表明，采用姿态机动路径重规划算法与自适应操纵律，在控制力矩陀螺部分失效的情况下，仍可以实现空间站的大角度姿态机动。姿态机动方法可以有效应对空间站大角度姿态机动过程中可能出现的SGCMG部分失效情况，从而提高空间站姿态机动任务的安全性与可靠性。

关键词：姿态机动；控制力矩陀螺；路径规划；操纵律

在空间站建造与运营的过程中，往往需要通过姿态机动来辅助完成交会对接、舱段转移等特定的任务[1]。空间站的姿态机动通常采用姿控发动机作为执行机构，采用这种方式需要耗费大量的燃料。控制力矩陀螺(Control Moment Gyroscopes, CMG)是一种角动量交换执行机构，仅需电能就能够进行工作，不需要消耗燃料[2]。然而，在姿态机动过程中，CMG持续地与空间站进行角动量交换，很容易出现饱和或奇异现象，从而失去控制能力。为了有效减少姿态机动任务中的燃料消耗，美国麻省理工学院的Bedrossian于1996年提出了零燃料大角度姿态机动(Zero Propellant Maneuver, ZPM)的概念[3]。2007年3月，NASA成功实施了国际空间站180°ZPM在轨飞行试验，节省了约50kg、价值约110万美元燃料[4-5]。ZPM的基本思想是通过构造最优控制框架，充分利用环境力矩与姿态动力学特性，规划合适的姿态路径与角动量轨迹，在姿态机动的过程避免CMG的饱和与奇异，从而实现零燃料消耗[6]。ZPM技术一方面可以避免姿态机动过程的大量燃料消耗，另一方面可以避免燃气对太阳帆板、外露设备和试验载荷的污染和影响。

作为一种姿态控制冗余执行机构，CMG很有可能因故障而出现部分失效，这会对姿态控制问题带来很大影响。国际空间站在运行过程中就曾出现陀螺部分失效的情况[1]。国内外已有学者对部分失效CMG的姿态控制问题开展了理论研究。Sands与Kim等以非冗余的三个单框架控制力矩陀螺(Single Gimbal Control Moment Gyroscopes, SGCMG)为研究对象，设计了无奇异角动量空间最优安装矩阵，并基于该设计实现了采用三个SGCMG的姿态机动[7]。Kasai与Kojima等通过构造操纵序列，实现了仅采用两个SGCMG的大角度姿态机动[8]。Yamada等与Kwon等分别采用Lyapunov方法与线性变参数(Linear Parameter Varying, LPV)方法实现了仅采用两个SGCMG的姿态速率阻尼与姿态定向[9-10]。目前虽然已有在操纵律构造与控制器设计等方面开展的研究，但都是基于在姿态机动控制任务之前SGCMG就已经部分失效的假设，并未针对在姿态机动过程中SGCMG的失效情况开展研究。而机动过程中可能出现的SGCMG部分失效的更大不确定性，将对姿态机动任务的完成带来更大的难度。

1SGCMG失效特性分析

为了实现三轴姿态控制，通常需应用由多个SGCMG组成的冗余系统。金字塔构型SGCMG是典型的冗余SGCMG系统，以金字塔构型的SGCMG作为研究对象。如图1所示，金字塔构型的SGCMG由四个SGCMG组成，框架轴矢量分别位于金字塔的四个侧面，角动量面与塔底面夹角均为β，β=54.73°。

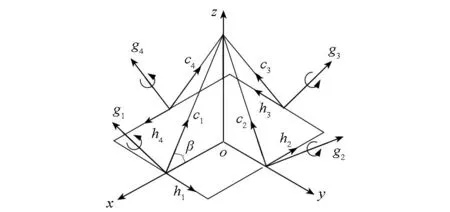
图1　金字塔构型SGCMGFig.1　Pyramid configuration SGCMG

SGCMG的饱和与奇异问题是限制其应用的重要因素。饱和是指所需的角动量超出SGCMG的外包络的现象，而奇异是指在SGCMG角动量包络的内部由于构形限制使SGCMG无法输出所需力矩的现象。当SGCMG出现部分失效时，其饱和与奇异特性也将发生很大的变化。

无论是饱和还是奇异状态，都可以通过解析推导并绘制奇异角动量超曲面的方法进行分析[11-12]。在奇异状态下，即任何一个SGCMG都不能提供指定方向的控制力矩，如式(1)所示。

u·ci(δi)=0(i=1,2,…,n)

(1)

其中，u是指令力矩方向单位向量，ci(δi)为每个SGCMG可提供的力矩方向单位向量。定义δS为SGCMG的奇异框架角状态。奇异角动量HS是控制力矩陀螺处于奇异框架角状态时的角动量[9]，可通过式(2)求得。

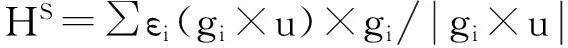
(2)

其中，gi为第i个SGCMG的框架轴方向单位向量。

第i个SGMG的奇异力矩方向单位向量为：

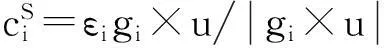
(3)

由于每个奇异状态δS都可能存在HS和-HS与之对应，两种情况可用式(4)的符号函数区别。

εi=sign(u·hi)

(4)

对于一个冗余的SGCMGs系统，每一个框架角状态δS都对应一个角动量HS，但并不是每一个奇异角动量HS都对应一个框架角状态，这是因为框架角是一个n维空间的量，而角动量是一个三维的量，对于一个奇异角动量状态δS，可能存在n-3维空间的奇异角动量HS对应这个δS。

奇异状态可划分为显奇异与隐奇异两类[9]。隐奇异可以通过SGCMG的零运动来脱离奇异状态，而SGCMG一旦陷入显奇异便很难脱离。奇异点的显隐性可通过判定矩阵Q的正定性得到。

Q=NTPN

(5)

金字塔构型的SGCMG由四个陀螺组成，即n=4。当一个陀螺发生失效时，仅有三个陀螺进行工作，所有的隐奇异点都将退化为显奇异点， 即角动量包络内部将仅存在显奇异点。那么，零运动操纵律将无法有效解决显奇异问题[9]，可采用引入力矩误差的鲁棒操纵律。关于操纵律的设计，将会在第3节中给出。

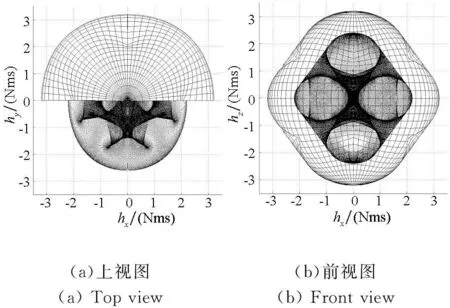
图2中的不规则网格半球为正常工作情况下的金字塔构型SGCMG角动量包络半球，内部由散点构成的曲面为单陀螺失效情况下奇异角动量曲面。由图2可知，当SGCMG的单个陀螺失效时，其角动量包络发生了很大的变化，角动量空间约缩小为原来的70%。因此，如果在大角度姿态机动的过程中，SGCMG发生了部分失效情况，需要对姿态机动路径与角动量路径进行重规划。对于角动量空间内部的内奇异面，需采用合适的操纵律进行规避。

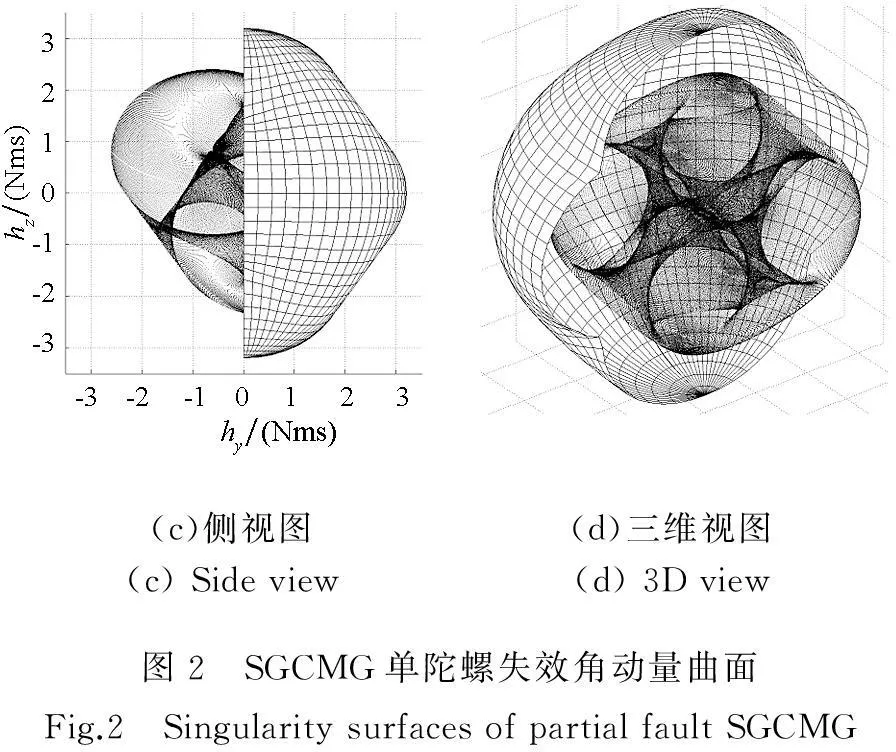
2姿态机动路径重规划

在姿态机动过程中，如果SGCMG始终能够正常工作，那么跟踪参考姿态机动路径完成机动，其参考姿态路径在机动实施之前就已经确定。如果在姿态机动过程中CMGs部分失效，那么需要对姿态机动路径进行重规划。姿态机动路径重规划的算法采用伪谱法，伪谱法是一种求解最优控制问题的间接法，近年来它被广泛应用于轨道优化、编队飞行及再入轨迹优化等方面的各类最优控制问题[13]。

Legendre伪谱法将状态变量与控制变量在勒让德-高斯-洛巴托(Legendre-Gauss-Lobatto，LGL)节点处同时离散，并采用Legendre多项式拟合状态变量与控制变量。n阶Legendre多项式可表示为：

(6)

(7)

状态变量与控制变量可由LGL节点处的离散量拟合得到，即

(8)

(9)

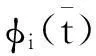
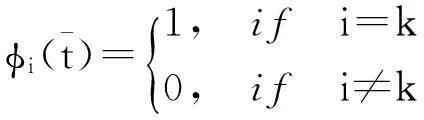
(10)

状态变量的微分可由LGL节点处的离散量计算。

(11)

其中，Dki为(N+1)×(N+1)矩阵的元素，由Legendre多项式计算。

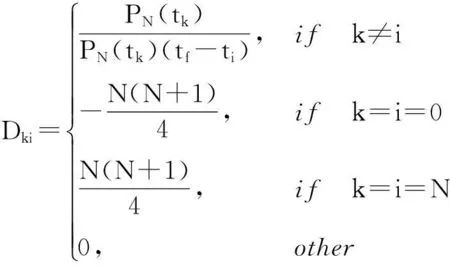
(12)

控制模型的微分方程可以转化为代数方程。姿态控制模型为：

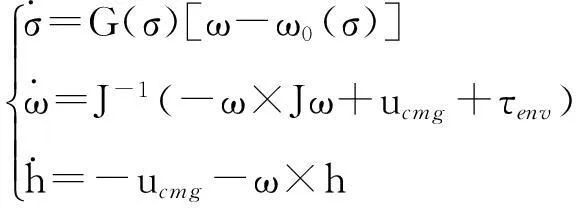
(13)

其中，σ为姿态修正的罗德里格斯参数，G(σ)表示为[(1-σTσ)I3/2+σσT+[σ×]]/2，ω是空间站的角速度，ω0(σ)是轨道角速度，J为空间站的转动惯量，ucmg为SGCMG控制力矩，τenv为环境力矩，h为控制力矩陀螺的角动量。

根据式(6)～(12)，可将式(13)中的微分方程转化为代数方程，如式(14)所示。

(14)

其中，σk,ωk与hk分别为LGL节点处的姿态、角速度与角动量。

同时，需要考虑边界和过程约束：

(15)

其中：hm为部分失效陀螺的角动量包络最小角动量半径，在姿态机动的过程中，角动量幅值要始终小于该值；σs与σf分别为初始、终端状态的姿态，ωs与ωf分别为初始、终端状态的姿态的角速度。

采用序列二次规划(Sequential Quadratic Programming， SQP)算法对由式(14)与式(15)所构成的非线性规划问题进行求解，采用SNOPT工具包进行求解，该工具包可以有效求解带有稀疏矩阵的非线性规划问题[14]。

3自适应操纵律设计

图3　单框架控制力矩陀螺工作流程Fig.3　Performing process of SGCMG

因此，需要设计合适的操纵律，实现在控制力矩陀螺部分失效情况下的自适应操纵。

定义失效向量为：

Eill=[γ1,γ2,γ3,γ4]T

(16)

当γi=1时，表示第i个陀螺正常工作；当γi=0时，表示第i个陀螺出现故障。该失效向量Eill不可以检测。控制力矩陀螺所输出的力矩为：

(17)

其中，C(δ)=Acosδ-Bsinδ，Mill=diag(Eill)。

由于C(δ)是通过δ计算得到的，当陀螺停转时，该陀螺的框架角和框架角速度仍然具有物理意义，仍然可以被检测。但是，该陀螺此时并不输出力矩。

构建一个用于检测控制力矩陀螺失效情况的函数。

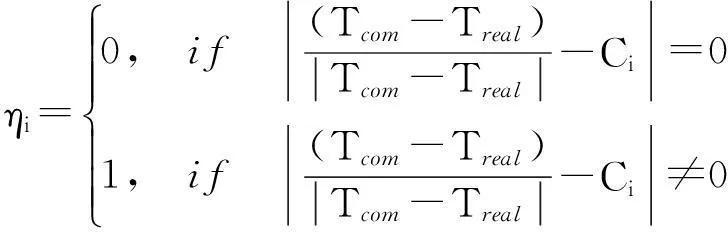
(18)

定义失效矩阵为：

(19)

该矩阵将作为检测信息反馈给操纵律。

非对称鲁棒逆操纵律可以有效规避SGCMG角动量空间内的隐奇异与内部显奇异空间[16-17]。对非对称鲁棒逆操纵律进行了改进，在非对称鲁棒逆操纵律中引入反馈矩阵，从而实现对SGCMG工作状态的自检测以及自适应操纵。定义自适应非对称鲁棒逆操纵律为：

(20)

式中：k为奇异系数，

(21)

W为非对称矩阵，

(22)

矩阵A为近似单位矩阵，

(23)

其中，

εi=ε0sin(ωt+φi)。

(24)

为了验证该操纵律的有效性，给出一个算例。给定输入指令力矩Tcom=[-0.8Nm0.5Nm1Nm]，设定在第80s第4个CMG失效。图4、图5给出了不同操纵律的对比情况。图4(a)、图4(b)与图4(c)为采用传统鲁棒操纵律情况下输出力矩、框架角与框架角速度变化曲线，图5(a)、图5(b)与图5(c)为采用自适应非对称鲁棒逆操纵律的变化曲线。由对比可知，传统鲁棒操纵律并不能及时响应控制力矩陀螺的失效状态，因此当一个陀螺失效时，控制力矩陀螺所提供的输出力矩与指令力矩存在很大偏差。当采用自适应非对称鲁棒逆操纵律时，失效情况可以及时被检测，并将该信息反馈给操纵律，从而调整操纵律的内部参数，实现操纵律自适应调整。由图5(a)可知，在该操纵律的作用下，输出力矩仅仅在CMG部分失效的瞬时出现较大的力矩偏差，此后输出力矩可以与指令力矩达到良好的吻合程度。

(a) 控制力矩变化曲线(a) Control torque versus time

(b) 框架角变化曲线(b) Gimbal angle versus time

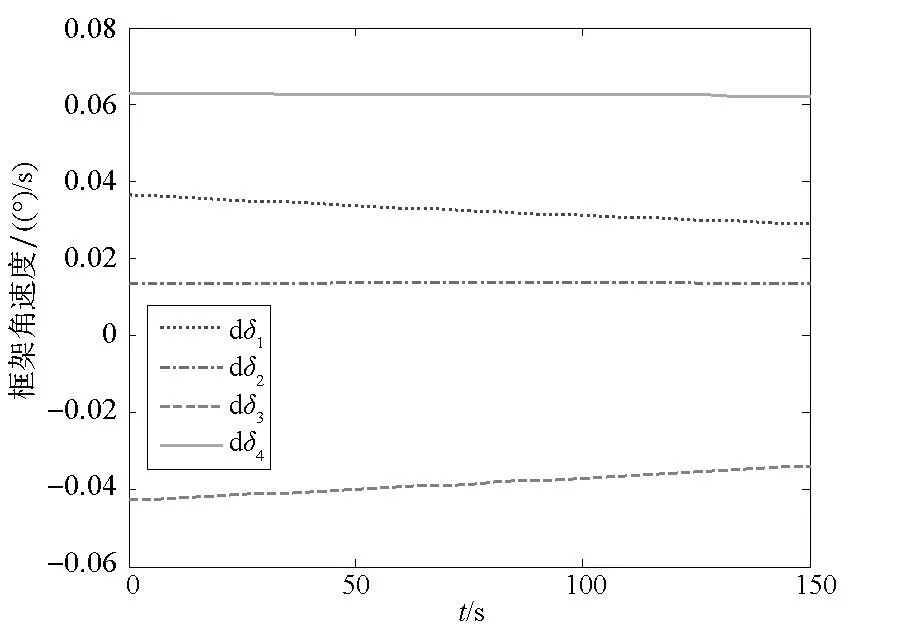
(c) 框架角速度变化曲线(c) Gimbal rate versus time图4　传统操纵律算例Fig.4　Traditional steering law

4仿真验证

设定空间站轨道高度约为380km，那么轨道角速度ω0≈0.0011rad/s。姿态机动时间为5000s，设定SGCMG部分失效时刻为3000s。空间站的角动量为diag(3×106kg·m25×106kg·m28×106kg·m2)。仿真结果如图6所示。

(a) 控制力矩变化曲线(a) Control torque versus time

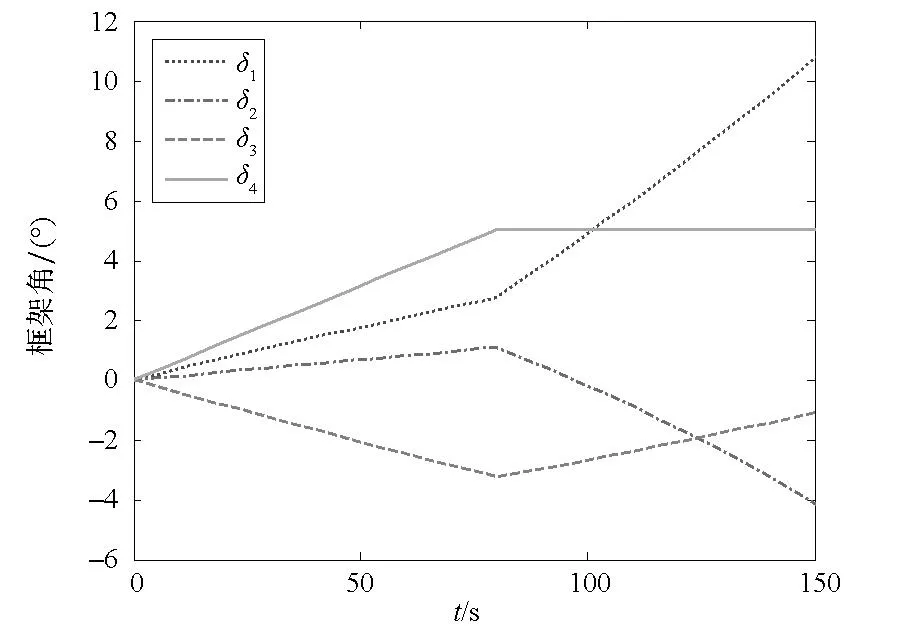
(b) 框架角变化曲线(b) Gimbal angle versus time

(c) 框架角速度变化曲线(c) Gimbal rate versus time图5　自适应操纵律算例Fig.5　Adaptive steering law

图6(a)与图6(b)分别为空间站姿态角与角速度的变化曲线，空间站实现了偏航90°的大角度姿态机动，且滚转与俯仰角变化约为10°。 图6(c)为SGCMG角动量变化曲线，由于在约3000s处SGCMG出现了部分失效，角动量曲线发生了突变。图6(d)为控制力矩变化曲线，控制力矩最大值不超过6Nm，在执行机构所能承受的范围内。图6(e)和图6(f)分别为SGCMG的框架角与框架角速度曲线，在约3000s处，陀螺4发生了失效现象，陀螺4不再提供角动量和控制力矩。图6(g)为角动量幅值变化曲线，由图6(g)可知，重规划角动量路径始终在最大允许值以内，并未发生饱和现象，说明重规划的机动路径是可行的。图6(h)为奇异测度变化曲线，由该图可知，采用自适应操纵律，一方面能够在SGCMG部分失效的瞬时(约3000s处)及时响应失效状态，另一方面，该操纵律还继承了传统操纵律在避免奇异方面的优势，在4400s附近接近奇异状态时，可以迅速脱离，从而使SGCMG始终提供有效的控制力矩，完成大角度姿态机动任务。

(a)姿态变化曲线(a)Attitudeversustime(b)角速度变化曲线(b)Angularrateversustime

(c)角动量变化曲线(c)Momentumversustime(d)控制力矩变化曲线(d)Controltorqueversustime

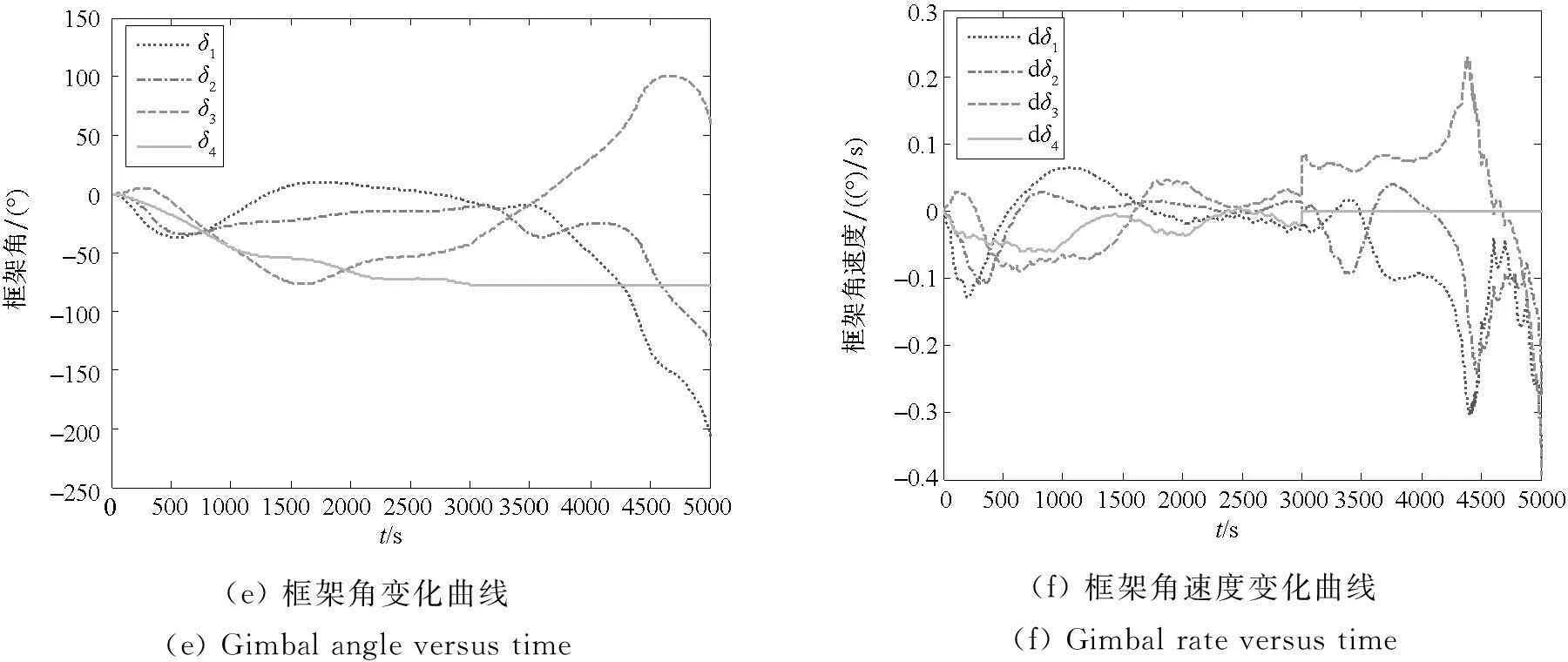
(e)框架角变化曲线(e)Gimbalangleversustime(f)框架角速度变化曲线(f)Gimbalrateversustime

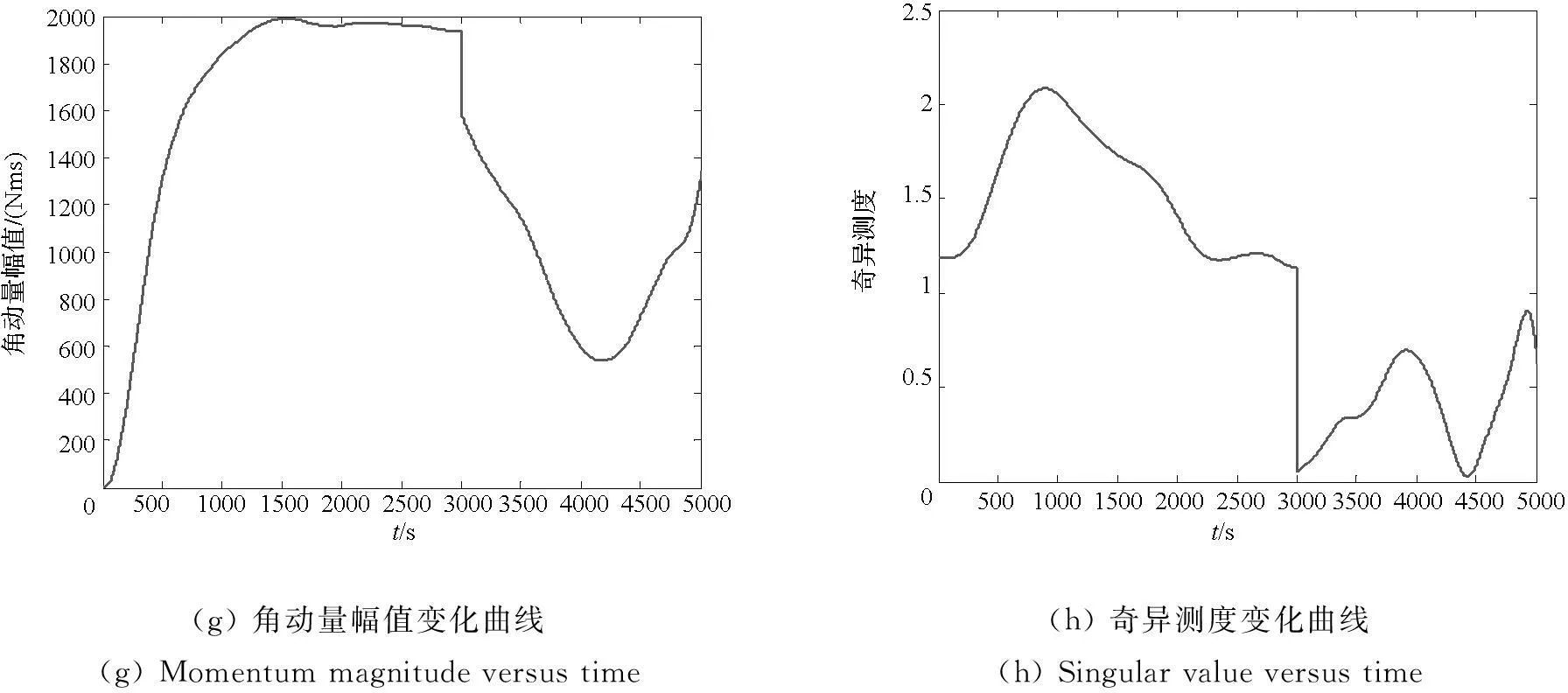
(g)角动量幅值变化曲线(g)Momentummagnitudeversustime(h)奇异测度变化曲线(h)Singularvalueversustime

图6仿真结果

Fig.6Simulation results

5结论

结合SGCMG失效的特点，采用伪谱法与序列二次规划求解重规划姿态机动路径。考虑了控制力矩陀螺失效情况的不可预测性，设计了自适应非对称鲁棒操纵律，该操纵律既可以继承传统操纵律在避免奇异方面的优势，又能及时响应失效状态从而进行自适应调节。算例分析表明，采用路径重规划策略与自适应操纵律，可以有效应对姿态机动过程中的部分失效问题，使空间站仍具备一定的姿态机动能力。该姿态机动策略，为空间站零燃料姿态机动任务的实施提供了有效的备份手段，从而提高姿态机动任务的安全性与可靠性。

参考文献(References)

[1]Fehse W. Automated rendezvous and docking of spacecraft[M].UK: Cambridge University Press, 2003.

[2]章胜, 黄海兵, 赵乾, 等. 控制力矩陀螺辅助的空间站大角度姿态机动 [J]. 国防科技大学学报，2013,35(4): 7-13.

ZHANG Sheng, HUANG Haibing, ZHAO Qian,et al. Study of control momentum gyroscopes assisting maneuver [J]. Journal of National University of Defense Technology, 2013,35(4):7-13.(in Chinese)

[3]Bedrossian N, Bhatt S, Kang W, et al.Zero-propellant maneuver guidance [J]. IEEE Control System Magazine,2009, 29(5): 53-73.

[4]Bedrossian N, Bhatt S. First ever flight demonstration of zero propellant maneuver(TM) attitude control concept[C]//Proceedings of AIAA Guidance, Navigation and Control Conference and Exhibit, 2007， AIAA 2007-6734：1-12.

[5]Bedrossian N, Bhatt S, Lammers M,et al. Zero-propellant maneuver flight results for 180deg ISS rotation [C]//Proceedings of the 20th International Symposium on Space Flight Dynamics, 2008: 4833.

[6]Kang W, Bedrossian N. Pseudospectral optimal control theory makes debut flight,saves NASA 1M dollars in under three hours[J]. Society for Industrial and Applied Mathematics News, 2007, 40(7)：1-3.

[7]Sands T A, Kim J J, Agrawal B N.Nonredundant single-gimbaled control moment gyroscopes [J]. Journal of Guidance Control and Dynamics, 2012, 35(2): 578-587.

[8]Kasai S, Kojima H, Satoh M. Spacecraft attitude maneuver using two single-gimbal control moment gyros [J]. Acta Astronautica, 2013, 84:88-98.

[9]Yamada K, Jikuya I, Kwak O. Rate damping of a spacecraft using two single-gimbal control moment gyros [J]. Journal of Guidance Control and Dynamics, 2013, 36(6): 1606-1623.

[10]Kwon S, Shimomura T,Okubo H.Pointing control of spacecraft using two SGCMGs via LPV control theory [J]. Acta Astronautica, 2011, 68(7): 1168-1175.

[11]Haruhisa K. A geometric study of single-gimbal control moment gyros [R]. Report of Mechanical Engineering Laboratory,1998, 105:108.

[12]Tang L, Xu S J. Geometric analysis of singularity for single-gimbal control moment gyro systems [J]. Chinese Journal of Aeronautics, 2005, 18(4): 295-303.

[13]Gong Q, Ross I M, Fahroo F. Spectral algorithm for pseudospectral methods in optimal control [J]. Journal of Guidance Control and Dynamics, 2008,31(3):460-471.

[14]Gill P E, Murray W, Saunders M A. User’s guide for SNOPT version 7: software for large-scale nonlinear programming[S]. Mountain View,USA:Stanford Business Software Inc 2006.

[15]吴忠,吴宏鑫. 单框架控制力矩陀螺系统操纵律研究综述[J]. 宇航学报, 2000, 21(4): 140-145.

WU Zhong, WU Hongxin.Survey of steering laws for single gimbal control moment gyroscope systems [J]. Journal of Astronautics, 2000, 21(4): 140-145. (in Chinese)

[16]Wie B. Singularity escape/avoidance steering logic for control moment gyro systems [J]. Journal of Guidance Control and Dynamics, 2005, 28(5): 948-956.

[17]Kurokawa H. Survey of theory and steering laws of single-gimbal control moment gyros [J]. Journal of Guidance Control and Dynamics, 2007, 30(5): 1331-1340.

http://journal.nudt.edu.cn

Space station attitude maneuver method considering partial fault of single gimbal control moment gyroscopes

ZHAOQian,TANGGuojin

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：The fault character of pyramid configuration single gimbal control moment gyroscopes (SGCMG) was analyzed. The calculation approach solving the replanned attitude maneuver path was proposed based on the Legendre pseudo spectral method. Considering the unpredictability of the SGCMG fault, an adaptive steering law was designed. Using this steering law, the fault state of SGCMG was detected and the parameters of the steering law was self-tuned. The simulation results reveal that, the large angle attitude maneuver can be accomplished by using the path replanned method and the adaptive steering law, when the SGCMG encounter partial fault. The proposed method can cope with the partial fault state of the SGCMG during attitude maneuver effectively, thus improving the security and reliability of the space station attitude maneuver mission.

Key words：attitude maneuver; control moment gyroscopes; path planning; steering law

中图分类号：V421.4

文献标志码：A

文章编号：1001-2486(2015)06-054-07

作者简介：赵乾(1987—)，男，辽宁康平人，博士研究生，E-mail：zhaoqianmars@gmail.com；唐国金(通信作者),男,教授,博士，博士生导师，E-mail：tanggj@nudt.edu.cn

基金项目：国家自然科学基金资助项目(11272346)；国家973计划资助项目(2013CB733100)

收稿日期：*2014-12-23

doi:10.11887/j.cn.201506012