长方体类光学元件形位误差高精度测量方法*
郭 蒙,戴一帆,彭小强,铁贵鹏
(1.国防科技大学 机电工程与自动化学院, 湖南 长沙 410073;
2.超精密加工技术湖南省重点实验室, 湖南 长沙 410073)
长方体类光学元件形位误差高精度测量方法*
郭蒙1,2,戴一帆1,2,彭小强1,2,铁贵鹏1,2
(1.国防科技大学 机电工程与自动化学院, 湖南 长沙410073;
2.超精密加工技术湖南省重点实验室, 湖南 长沙410073)
摘要:如何实现长方体元件光学面形位误差的高精度测量以及怎样利用测量数据对这些误差进行修正加工是制造过程中的主要问题。提出一种基于波面干涉的长方体类光学元件形位误差测量方法,借助大口径干涉仪和高精度端齿盘搭建测量系统,实现了长方体类光学元件1μm/400mm精度的平行度和垂直度测量,获得了高精度的形位误差综合分布数据,并利用磁流变、小磨头数控抛光等现代光学加工手段实现了此类光学元件的高精度加工。
关键词:长方体光学元件;形位误差;平行度误差;垂直度误差;修形加工
长方体类光学元件是光学加工与制造领域中一类重要的对象类别,在某些尖端技术产品中发挥着无可替代的作用。长方体类光学元件不仅对光学表面传统的面形、波纹度、粗糙度等形状指标有较高的要求,同时还要求有相互位置关系的光学面之间的位置误差能够保持在非常小的公差范围之内。例如:光刻机是集成电路制造中最为重要的加工设备,其性能直接决定了光刻微细图形的传递能力,与微电子器件超大规模化直接相关。而作为光刻机的关键分系统之一的工作台测量方镜就是典型的长方体类光学元件,其形位误差要求在440mm长度上达到2um以下(1″),加工和检测的难度极高。随着光学制造技术的发展,长方体类光学元件已经越来越成为一些领域光学系统中影响总体性能的关键,其形位误差高精度测量和加工问题亟待解决。而目前对于长方体类光学元件的检测方法研究还不成体系,较好的测量理念急需补充发展。解决这一类光学元件形位误差的检测方法,形成一套合理的标准化评价方案,并能实际指导此类元件的加工和制造,对于尖端技术产品精度性能和可靠性的提升具有突破性的意义。
1光学元件形位误差测量研究现状
国外对形位误差的研究在19世纪末就已开始,至今已形成了系统性的测量理论、测量标准及相关设备的研究。中国从20世纪70年代末开始对形位误差进行较系统的研究,近四十年来取得了大幅的进步,但与世界先进水平还有很大差距[1]。在形位误差检测国家标准中,针对不同的测量对象、测量条件、测量环境及测量精度规定了多种测量方法。三坐标测量机是现代工业普遍采用的形状和尺寸检测设备,其最大的特点是通用性强[2]。通过测头采集一些点来计算误差值,由于采集到的数据有限,获得的形位误差分布数据不便用于确定性误差修正加工,而且精度有限。激光测量基于夫琅和费单缝衍射原理,利用激光单色性好、方向性好、脉冲宽度窄的特点,属于非接触式测量,能克服一般测量方法的缺陷,而且装置简单,测量精度较高[3]。自准直仪可以实现多面棱镜、角度块垂直度的快速测量[4],可以用作小角度的精密测量,一般配合多齿分度盘使用。配合平面反射镜使用时,则可以用于测量直线度、平面度、平行度和垂直度。配合高精度的设备,采用不同的测量方法,自准直仪可以达到0.5″的精度。用激光测量或自准直仪可实现形位误差的快速检测,具有测量装置简单、数据处理方便、测量结果精确度高等优点,但都不能获得被测面的误差分布,无法指导确定性修形加工[5]。
波面干涉测量法的优点在于可以通过合适的测量光路获得高精度的形位误差分布数据,能够直接用于确定性修形加工。意大利学者Vannoni和Bertozzi[6]针对小型量块的相对表面平行度提出了如图1的测量方案。激光干涉仪发射出的平行光线一部分经过参考平面反射作为参考光,另外一部分照射在被测件的两个表面上,其反射光按照光路可逆反射至参考平面,并与参考光发生干涉产生两个干涉条纹。将两个干涉条纹进行数据处理后,可以得到被测物体两表面的平面度和平行度信息。

图1 不透明量块的平行度测量方案Fig.1 Parallelism measurement method of opaque gauge
在测量垂直度的研究中,Bhattacharya等[7-8]提出了如图2所示的测量方法测量直角棱镜的直角差,原理类似于上述的测量方法。光路经过直角棱镜直角边的两次反射,与原参考光形成干涉条纹。这种方法针对对称式误差具有较好的测量效果,但仅适用于内垂直度的测量。

图2 直角棱镜垂直度测量方案Fig.2 Verticality measurement method of the right angle prism
2基于波面干涉的长方体类光学元件形位误差测量方法
波面干涉测量法能够获得被测面高精度的面形误差分布数据,可以直接用于确定性修形加工。对于长方体类光学元件的形位误差,同样希望通过干涉测量的方法,获得形位误差全息分布数据,从而指导修形加工,提高加工效率。以长方体空气静压导轨的测量和加工过程为例,该导轨属于高精度轴系部件,尺寸为440mm×200mm×80mm,为保证性能,对导轨工作面的平行度和垂直度提出了较高要求。设计时采用玻璃作为导轨材质,为解决其平行度和垂直度高精度测量问题,借助高精度端齿盘和大口径干涉仪搭建形位误差光学测量系统,如图3所示。通过三十六棱镜的一组平行面及对应的垂直面对高精度端齿盘进行轴线校准,然后利用端齿盘分度精度高的特点,使用大口径波面干涉仪对待测件形位误差进行检测,获得待测件形位误差的全息分布数据,然后根据误差数据借助光学加工手段,使误差不断收敛。

1—大调整台;2—高精度端齿盘;3—小调整台;4—高精度三十六棱镜。图3 形位误差测量系统组成Fig.3 Shape and position error measurement system
测量系统主要由大调整台、高精度端齿盘、小调整台、高精度三十六棱镜及波面干涉仪组成。大调整台、端齿盘和小调整台之间由螺钉连接固定。大调整台由台面和3个可调高度的螺纹支撑脚组成,通过调节垫脚高度可以调整台面的俯仰倾斜角度。高精度端齿盘具有精确的分度功能,精度可达0.2″,并可以旋转一定的角度后锁死。小调整台则是光学系统中常见的角度调整平台,通过螺纹旋钮调节台面的俯仰倾斜角度。三十六棱镜是光学检测中常用的辅助检测器件,经检定,棱镜侧面角度偏差为0.4″。波面干涉仪为实验室采购设备,测量口径为24 inch。
测量方案操作步骤如下:
步骤一:利用三十六棱镜对测量系统进行校准,具体包括以下操作:
首先大调整台置于波面干涉仪气浮平台上,正对干涉仪反射镜。然后用内六角螺钉将高精度端齿盘固定在大调整台相应位置,再将小调整台置于端齿盘回转平面,用螺钉固定。三十六棱镜放在小调整台上,选取棱镜的一个侧面正对干涉仪上,标记此侧面为1#面,同时按逆时针方向每隔90°依次标记棱镜的2#,3#,4#面。
1)将标准三十六棱镜的1#面对准干涉仪,微调小调整台使反射光斑出现在视场内;
2)端齿盘旋转180°,使3#面对准干涉仪,由于端齿盘回转轴线的偏差,此时3#面反射光斑与之前1#面反射光斑分别居于视场上下半部,且与视场中央横线的距离大体一致。慢慢调节大、小调整台俯仰角度并旋转端齿盘观察1#和3#面反射光斑,使两个光斑均位于中央横线上(如图4所示);

图4 校准端齿盘轴线示意图Fig.4 Sketch of the axis calibration of the indexing plate
3)旋转端齿盘使2#面正对波面干涉仪镜头,与第2步操作相同,通过调节大、小调整台的俯仰角度使2#面和4#面反射光斑也落在中央横线上;
4)顺次观察四个侧面反射光斑位置,微调小调整台使其落在视场十字线中央,此时校准完毕,端齿盘回转轴线与干涉仪光路垂直,取下标准棱镜。
步骤二:对长方体元件的平行度和垂直度进行测量,过程如下:
1)长方体导轨4个工作面依次标记为1#~4#面,将待测方镜放在小调整台上使1#面正对波面干涉仪镜头。用点胶的方式将导轨固定。
2)转动端齿盘,使方镜的4个待测工作面依次对准干涉仪,观察反射光斑的位置。只调整小调整台的俯仰角度,使4个待测工作面的反射光斑位于十字线中央。
3)将1#面正对干涉仪,测量软件将视场光斑模式切换为条纹模式。将1#待测面的反射条纹调至最稀疏,记录全息测量数据。端齿盘顺次转动90°,记录其余待测面的测量数据。测量过程中始终保持大调整台不动。测量结果如图5所示,形位误差均在1μm内。
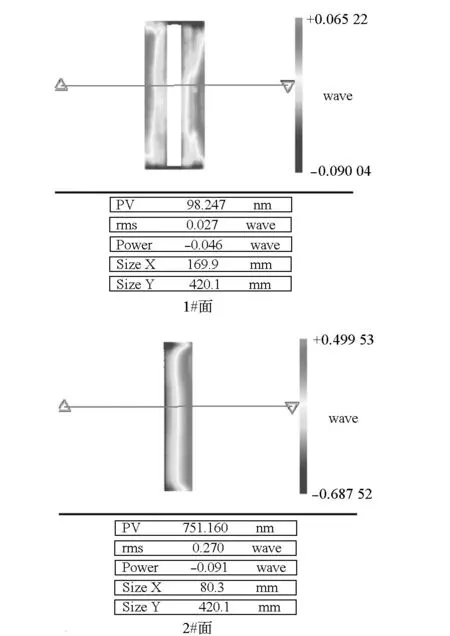

图5 导轨工作面形位误差测量结果Fig.5 Measurement results of the shape and position error of the guide working surface
3测量系统误差分析
测量系统调试过程分为校准和测量两个阶段,相应的测量误差也主要来源于这两个过程。校准过程主要是标定端齿盘的位姿,测量过程则需要调节工件回转轴线与端齿盘轴线的重合。因此误差分析从端齿盘轴线与干涉仪光路的垂直度偏差及工件轴线与端齿盘回转轴线的重合度偏差两方面讨论。
1)端齿盘回转轴线与干涉仪光路的垂直度偏差。该偏差主要是由标定过程中标准三十六棱镜的精度决定的。为简便起见,将垂直度偏差分解为绕x方向的偏转偏差和绕y方向的俯仰偏差,如图6所示。俯仰偏差对测量影响较大,其值主要由标准棱镜的对侧面平行度决定。假设标准镜的平行精度为α,则z轴的俯仰偏差为α/2,如图7所示。偏转偏差由另外一组对侧面以及四个侧面的误差耦合关系共同决定,误差值在α/2之内。该偏差在实际测量中对测量精度的影响不大,但会造成被测面绕激光方向的偏转,使测量尺寸与实际尺寸产生偏差。

图6 端齿盘坐标系Fig.6 Coordinate system of the indexing plate
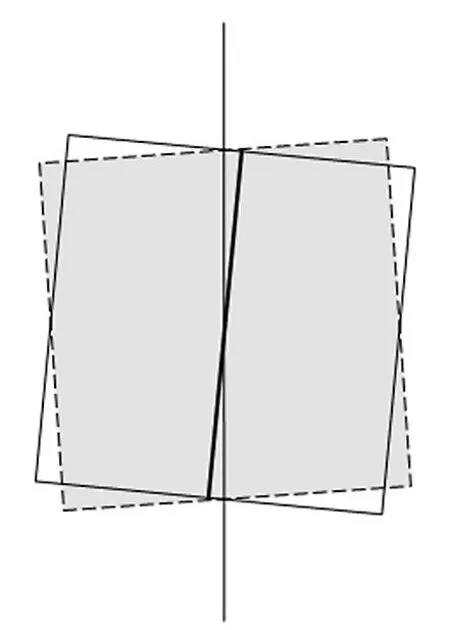
图7 俯仰偏差与平行度的关系Fig.7 Relationship between pitch deviation and parallel degree
2)工件轴线与端齿盘回转轴线的重合度偏差。长方体导轨的相邻两工作面起到定位基准的作用,用以标定导轨轴线。从测量调试过程中可知,选定的导轨两相邻工作面之间的垂直度对标定起到重要作用,因此在上光路调试前应尽量减小这两个侧面的垂直度误差。在实际测量中,其余两个工作面起到辅助标定的作用。类似地可将导轨轴线与端齿盘轴线的重合度偏差分解为俯仰和偏转两个方向的分量,将第一个侧面干涉条纹调节到最少,认为此时导轨轴线已经与端齿盘轴线重合。通过顺次调节各个侧面,使干涉条纹尽量不产生横条纹,根据四个侧面的耦合关系可知偏转误差为α/2。
综合上述分析,测量系统的误差主要是由端齿盘轴线的俯仰偏差和工件轴线与端齿盘轴线在偏转方向上的误差造成的,并且二者具有耦合关系。此外,端齿盘平面内的回转精度也会产生一定的影响。
如图8所示,x轴和y轴分别为工件理想侧面的法向,工件转动时理想回转轴线为z轴,实际回转轴线在以O为顶点,以z轴为对称轴的圆锥区域内,圆锥顶角为α。设A为竖坐标为1的圆锥面内一点,OA与z轴的角度是α/2,端齿盘回转误差为β,则测量误差最大为α/2+β。实际操作中,标准三十六棱镜一组平行面的平行度误差为0.4″,高精度端齿盘回转误差为0.2″,因此该测量系统的形位误差测量精度为0.4″。

图8 测量误差示意图Fig.8 Sketch of measurement error
4形位误差加工
由上述测量系统可以直接得到带有形位误差分布数据的长方体导轨各工作面面形,利用磁流变、小磨头数控加工等手段,使测得的工作面面形不断收敛,即可获得较高的形位误差精度。图5所示为本次加工导轨的最终误差测量结果,导轨的平行度和垂直度都在1μm以内,实现了长方体导轨形位误差的高精度测量和加工,证明了本测量系统对于长方体类光学元件形位误差测量和指导加工的有效性。
5结论
针对长方体类光学元件,基于波面干涉测量的形位误差高精度测量方法能够获得被测面综合的形状误差和位置误差全息分布数据,可以直
接指导确定性修形加工。通过实际加工实验,验证了方案的可行性。相比传统的测量方法,提出的检测和加工方案在精度和效率上都有较大的提升。
参考文献(References)
[1]郑育军, 黄富贵. 国内外形位误差研究进展[J]. 工具技术, 2006, 40(11):10-13.
ZHENG Yujun, HUANG Fugui. Summary of research and development on form & position errors in home and abroad[J].Tool Engineering, 2006, 40(11):10-13.(in Chinese)
[2]赵丽娟, 马和, 程俊廷. 激光在垂直度误差测量中的应用[J]. 工业计量, 2003, 13(5):35-36.
ZHAO Lijuan, MA He, CHENG Junting. Application of laser in verticality tolerance measurement[J].Industrial Measurement, 2003, 13(5):35-36.(in Chinese)
[3]李树波. 自准直仪在垂直度测量中的应用[J]. 计量技术, 2001, 1(2):58.
LI Shubo.The application of the autocollimator in the measurement of the verticality [J].Measurement Technique,2001, 1(2):58.(in Chinese)
[4]吴敏镜, 易维坤, 周安石.惯性器件制造技术[M].北京:中国宇航出版社, 1988:78-82.
WU Minjing,YI Weikun,ZHOU Anshi. Manufacturing technology for inertial component[M].Beijing:China Astronautic Publishing House, 1988:78-82.(in Chinese)
[5]郑子文, 刘景坡, 陈善勇. 内表面间垂直度的高精度测量方法设计与误差分析[J]. 国防科技大学学报, 2009, 31(4):36-41.
ZHENG Ziwen, LIU Jingpo, CHEN Shanyong.A high precision perpendicularity measurement method and analysis for internal surfaces[J].Journal of National University of Defense Technology, 2009, 31(4):36-41.(in Chinese)
[6]Vannoni M, Bertozzi R. Parallelism error characterization with mechanical and interferometric methods[J]. Optics and Lasers in Engineering, 2007, 45(6):719-722.
[7]Bhattacharya J C. Measurement of parallelism of the surfaces of a transparent sample[J]. Optics and Lasers in Engineering, 2001, 35(1):27-31.
[8]Vannoni M M V, Molesini G. Joint interferometric measurement of planarity and parallelism[J]. Optical Engineering, 2004, 43(5): 12-20.
http://journal.nudt.edu.cn
Shape and position error measurement of cuboid optical element in high precision
GUOMeng1,2,DAIYifan1,2,PENGXiaoqiang1,2,TIEGuipeng1,2
(1. College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China;
2. Hunan Key Laboratory of Ultra-precision Machining Technology, Changsha 410073, China)
Abstract:How to realize the high-precision measurement of the shape and position errors of the cuboid optical element and how to use the measurement data to correct these errors are the main problem in the manufacturing process. A shape and position errors measurement method of the cuboid optical elements based on the wave-front interference theory was presented and the measurement system with large aperture instrument and high-precision indexing plate was built. With the help of this system, the parallelism and verticality measurement of the cuboid optical element in the accuracy of 1μm/400mm was achieved and the high-accuracy integrated distribution data of shape and position errors were obtained. The high-accuracy machining of this kind of optical element was achieved by using modern optical machining technology as magnetorheological finishing and computer controlled optical surfacing.
Key words:cuboid optical element; form and position error; parallelism error; verticality error; face machining
中图分类号:TN95
文献标志码:A
文章编号:1001-2486(2015)06-021-05
作者简介:郭蒙(1988—),男,陕西榆林人,博士研究生,E-mail:gmfine-0618@163.com;铁贵鹏(通信作者),男,讲师,博士,E-mail:Tieguipeng@163.com
基金项目:国家自然科学基金资助项目(51275521)
收稿日期:*2015-10-28
doi:10.11887/j.cn.201506005

