线性可调音速喷嘴工作特性仿真*
成 鹏,李清廉,张新桥,康忠涛,陈慧源
(国防科技大学 高超声速冲压发动机技术重点实验室, 湖南 长沙 410073)
线性可调音速喷嘴工作特性仿真*
成鹏,李清廉,张新桥,康忠涛,陈慧源
(国防科技大学 高超声速冲压发动机技术重点实验室, 湖南 长沙410073)
摘要:为了满足组合发动机模态转换的要求,连续稳定调节推进剂流量十分关键。为此,针对气体推进剂,在常规音速喷嘴的基础上设计了一种可调音速喷嘴。通过塞锥改变音速喷嘴的节流面积,进而实现流量的连续调节。采用两次包络线方法设计塞锥型面,使得可调音速喷嘴具有线性的流量特性。采用计算流体动力学数值仿真研究可调音速喷嘴的工作特性。仿真结果表明反压小于临界反压时,可调音速喷嘴流量不受反压影响。可调音速喷嘴保持临界状态的临界反压比随流量的减小呈增大的趋势。线性可调音速喷嘴的流量与塞锥位置有较好的线性关系,其流量系数高且几乎不受塞锥位置的影响。
关键词:可调音速喷嘴;线性;流量特性;流量调节;反压
火箭基组合循环(Rocket-Based Combined Cycle, RBCC)与空气涡轮火箭(Air Turbo Rocket, ATR)推进系统是当前的研究热门[1]。大空域大速度范围飞行要求推进系统根据不同的飞行状态进行工作模态转换。比如RBCC从起飞到速度为3Ma过程中,发动机工作在引射模态,当飞行到一定速度后其工作在冲压模态,当飞行到低地球轨道后其又工作在纯火箭模态[2]。ATR同样也存在类似的工况转换。
不同工况之间的稳定转换对于发动机的正常高效工作意义重大。RBCC和ATR的核心部件之一分别是引射火箭和燃气发生器,工况的转换主要由引射火箭和燃气发生器完成。基于火箭发动机的引射火箭和燃气发生器的工况转换通过调节推进剂流量实现,因此能够在大范围内稳定快速调节推进剂流量十分关键。
目前,氧气/煤油推进剂由于具有无毒无污染、热值高的优点,在组合发动机领域应用前景被看好[3]。对于氧气这类气体流量的调节,目前广泛采用的一种比较有效的方法是调节阀[4],但是普通调节阀的流量调节受下游环境的影响较大,达不到快速、稳定、精确流量调节的要求。
音速喷嘴是最常用的气体标准流量计之一,因其结构简单坚固、准确度高、重复性好,有着广泛的应用[5-6],但音速喷嘴型面是固定的,只能用于流量校验或控制。由一维等熵流动理论可得音速喷嘴临界状态下的流量:

(1)
式中,p0,At,T0,γ,Rg分别为喷嘴入口总压、喉部面积、入口总温、比热比、气体常数。
由式(1)可以看出,音速喷嘴流量与喉部面积成正比,而与下游环境无关。因此在给定入口气体参数后,通过调节喉部面积对流量进行调节是一种直接有效的方法。在音速喷嘴的基础上,增加塞锥装置,通过轴向移动塞锥改变喉部面积进而调节流量,如图1所示。可调音速喷嘴继承了音速喷嘴流量不受下游环境影响的优点,在流动壅塞的前提下,改变出口压力不影响流量[7]。因此,当下游压力波动时,可调音速喷嘴仍然可以保持稳定的流量,这对发动机稳定工作意义重大。

图1 常规音速喷嘴(左)与可调音速喷嘴(右)剖视图Fig. 1 Normal sonic nozzle (left) and throttleable sonic nozzle (right)
音速喷嘴已经标准化,历史上对音速喷嘴进行了详细的研究。Park[8]通过试验研究了音速喷嘴入口形状对流量系数的影响,认为入口越长越有利于防止流动分离、提高流量系数。Bignell等[9]研究了温度对小音速喷嘴工作特性的影响。Li等[10]采用数值仿真的方法研究了音速喷嘴扩张角对流量系数的影响。Lim等[11]采用水蒸气作为流动介质,通过试验研究了气体湿度对音速喷嘴特性的影响。Chao等[12]研究了音速喷嘴壁面粗糙度对流量系数的影响。音速喷嘴的流量特性至关重要,因此研究者们针对音速喷嘴流量特性进行了大量的工作[13]。对于可调音速喷嘴,其流量特性同样十分重要。Cao等[14]给出了一种与可调音速喷嘴类似结构的流量调节阀并对阀门处于一个开度的工况进行了仿真研究。
目前,还没有公开文献对可调音速喷嘴在流量调节过程中的流量特性、工作范围进行相关报道。流量调节过程中,塞锥位置如何影响可调音速喷嘴流量特性以及保持临界状态的临界反压都还有待研究。掌握可调音速喷嘴流量调节过程中的工作特性,对指导可调音速喷嘴的设计和工程应用具有积极意义。
1数值仿真基础
1.1 线性可调音速喷嘴结构设计
变推力火箭发动机中一般都要求推力具有线性调节能力[15-16],这就要求流量调节与塞锥位移之间为线性关系。线性的流量特性使得整个调节范围内具有相同的流量调节分辨率,同时还将简化控制方法,更方便调节。张育林[17]给出了线性可调文氏管的设计思路,该方法通过修正锥形调节锥得到线性流量特性的调节锥型面。杨明[18]给出了一种基于包络线的阀芯型面设计方法,文献中给出了求解阀芯型面的理论分析。但是该方法不适用于一般阀座型面。采用两次包络线的方法能够弥补上述不足,能对具有一般阀座型面的阀芯型面进行设计[19]。可调音速喷嘴入口位置型面为圆弧,可采用两次包络线方法进行设计。
图2给出了可调音速喷嘴的结构示意图。可调音速喷嘴主要由音速喷嘴、塞锥和阀体构成。转动调节手轮,塞锥在丝杠作用下可以沿轴向运动实现喉部面积的调节。丝杠仅用在实验室研究可调音速喷嘴工作特性时调节塞锥,实际应用中塞锥采用电机驱动。
线性流量特性通过塞锥型面保证,因此线性可调音速喷嘴的关键在于塞锥型面。设计参数入口总压为2MPa,流量为0.4~1.4kg/s,塞锥总行程设计为50mm,流量在行程范围内随行程线性变化。采用二次包络线方法设计塞锥型面,图3给出了塞锥在其局部坐标下的型面曲线。设计流量和塞锥位置之间的关系为:

(2)

根据式(1)计算得到对应的节流面积为:
A=-4.71×10-6L+3.14×10-4
(3)
式中,A为节流面积,单位m2。
求得塞锥型面后采用搜索法得到实际节流面积与塞锥位移之间的关系,如图4所示。从图中可以看出节流面积线性程度高,残差小于1‰,节流面积与塞锥位移之间的拟合方程如式(4),与方程式(3)十分接近,可见型面满足设计要求。
A=-4.706×10-6L+3.139×10-4
(4)
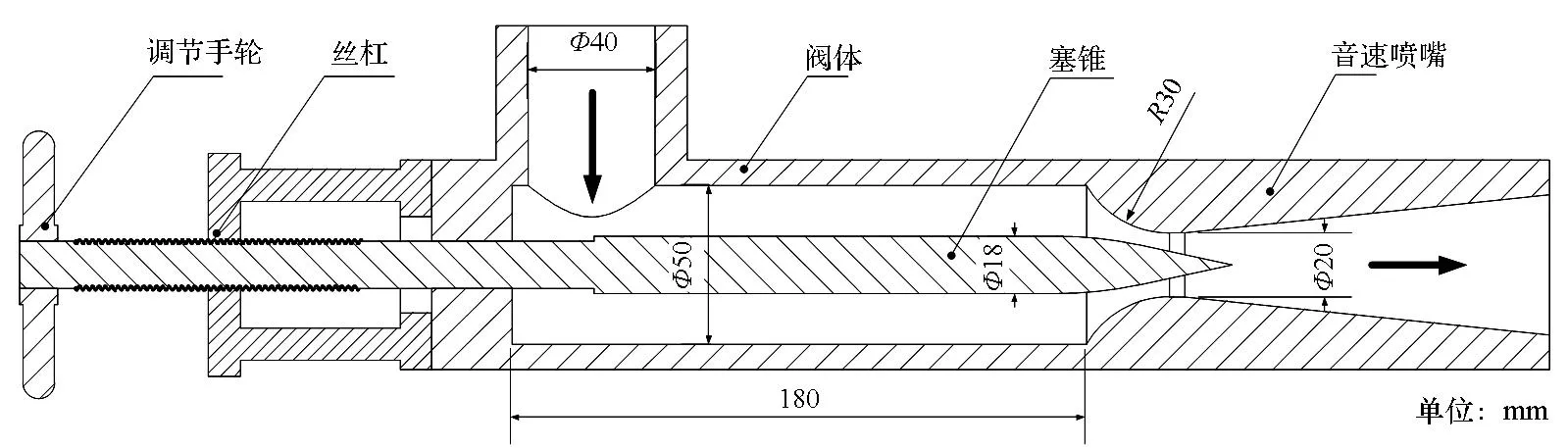
图2 可调音速喷嘴结构示意图Fig.2 Configuration of throttleable sonic nozzle

图3 塞锥型面设计结果Fig.3 Contour design of the plug

图4 塞锥型面设计数值验证结果Fig.4 Numerical verification of the plug contour
1.2 计算方法与网格
根据音速喷嘴内型面,适当简化后建立如图5所示的计算模型。为了方便划分结构网格,在90°转角位置采用了非一致网格。同时,在塞锥顶尖处用少量的非结构网格用以过渡。
在Fluent环境下进行数值仿真,采用基于密度的定常求解器求解三维N-S方程。假设气体介质为理想气体,湍流模型为标准k-ε模型。图5中同时给出了边界条件的设定,入口设置为压力入口(总压为2.0MPa),出口为压力出口(压力为1.5MPa),固体壁面为无滑移边界。用入口条件初始化全场进行迭代计算得到收敛解。
设计网格总数量约110万和170万两套网格进行网格无关性验证。图6给出了不同网格数量计算得到的直线上马赫数分布曲线,由图可见两套网格计算结果基本一致,因此后面的仿真研究网格数量均在110万左右。

图5 数值仿真计算网格及边界条件Fig.5 Meshes and boundary conditions of numerical simulation

图6 直线上马赫数分布曲线(x=0,z=0)Fig.6 Distribution of mach number along line(x=0,z=0)
2结果与讨论
保持正常工作的临界反压以及流量特性是可调音速喷嘴的两个重要工作特性。因此主要针对可调音速喷嘴在流量调节过程中塞锥位置对临界反压比和流量系数的影响进行讨论。
2.1 塞锥位置对临界反压比的影响
前文提到,可调音速喷嘴正常工作必须达到临界状态,即喉部流动速度达到声速。上游压力一定时,音速喷嘴出口压力低于临界反压[pe]才能达到临界状态。定义临界反压比为出口临界反压与入口总压的比值:
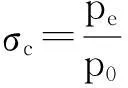
(5)
为了得到可调音速喷嘴在不同流量时正常工作的临界反压比,分别对塞锥位于0mm,10mm,20mm,30mm,40mm,50mm(流量依次减小)处进行了数值仿真。在仿真过程中不断提高反压,直到音速喷嘴失去临界状态,得到临界反压比。
图7给出了塞锥位于30mm时流量随反压变化曲线,从图中可以看出,当反压低于1.85MPa时流量均为0.778kg/s,当反压大于1.85Mpa后,流量迅速下降,因此可以近似认为临界反压为1.85MPa。

图7 塞锥位于30mm处流量随反压变化曲线Fig.7 Mass flow rate versus back pressure (L=30mm)
当喉部处于临界状态时,随着反压增大,在音速喷嘴扩张段内出现激波,且不断往喉部移动。图8是反压Pe为1.5MPa、塞锥位于30mm位置时对称面上的马赫数分布图,可以看到在扩张段内出现了激波,但此时喉部流动速度仍然处于临界状态,可调音速喷嘴正常工作。随着反压进一步增大,激波移动到无限接近喉部的位置。此时喉部流动速度仍然是声速,若反压继续增大,喉部将达不到声速,因此此时的反压即为临界反压。根据气体动力学理论,激波越靠近喉部,激波的强度越弱。当反压达到临界反压时,在喉部存在一个无限弱的激波,因此流动仍然是等熵的。由气体动力学知识[20],根据一维等熵理论由面积比可以得到:
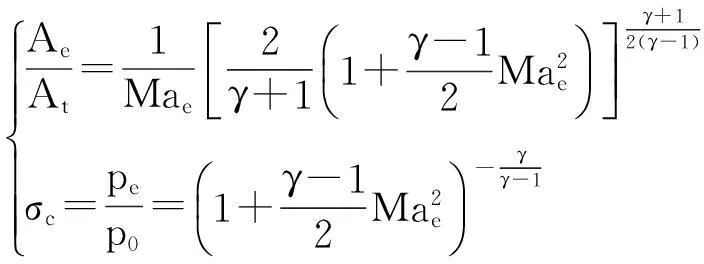
(6)

图8 对称面上马赫数分布图(L=30mm, pe=1.5MPa)Fig.8 Distribution of mach number in symmetry plane (L=30mm, pe=1.5MPa)
其中,At,Ae,γ,Mae分别为喉部面积、喷嘴出口面积、比热比、出口马赫数。
对于可调音速喷嘴,不同的塞锥位移对应不同的喉部面积,因此根据式(6)可以得到一维理论情况下的临界反压比与塞锥位置的变化曲线。图9给出了理论分析和仿真得到的临界反压比随塞锥位置变化的曲线。从图中可看到仿真得到的临界反压比低于理论计算值,这与理论计算为一维等熵假设有关。从图中还可以看出随着塞锥位置深入,流量减小,临界反压比略有增大,最后趋于稳定。
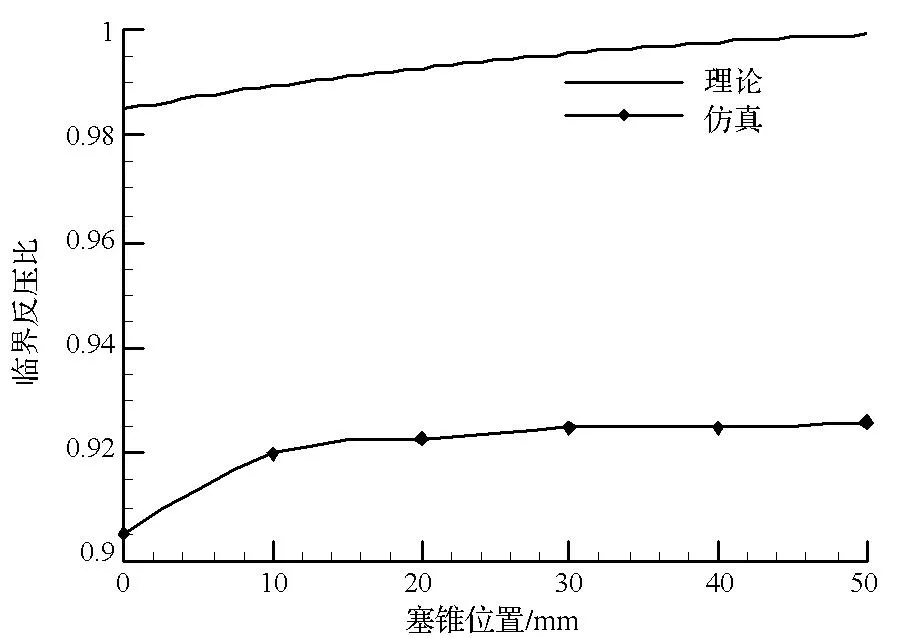
图9 临界反压比随塞锥位置的变化Fig.9 Critical back pressure ratio versus plug position
2.2 流量特性
线性可调音速喷嘴的塞锥型面采用两次包络线方法设计,具有线性的流量特性。
图10给出了线性可调音速喷嘴流量特性曲线,从图中可以看出可调音速喷嘴流量特性的线性程度高,仿真流量比较接近理论流量。采用线性模型对仿真流量进行拟合,拟合方程为式(7),其与式(2)中流量公式非常接近。拟合效果参数确定系数R2(adjusted)为0.999,十分接近1,由此可见线性拟合效果很好,流量特性线性程度高。

(7)
图中同时给出了流量系数Cd,流量系数定义为:

(8)

图10 可调音速喷嘴流量特性曲线Fig.10 Flow characteristic of throttleable sonic nozzle
从图中可以看到,塞锥位于10mm~50mm时,流量系数相差不大,约为0.963。工况中可调音速喷嘴节流面位置Re>106,而对于工业标准音速喷嘴,当Re>106时流量系数在0.99以上[13]。研究中可调音速喷嘴流量系数比较接近标准音速喷嘴,偏低的一个原因是塞锥对流场的干扰,另一个是塞锥增加了气体所受摩擦力。
另外,从图中还能看出塞锥位置为0mm时,流量系数明显低于其他位置,约为0.941。这是由于塞锥顶尖位于节流面附近,塞锥型面对流场的影响所导致。
图11为塞锥位于0mm和10mm位置喉部附近的马赫数分布。从等值线上可以看到,流场在几何对称轴上下略有不对称,这是由于气流在进入音速喷嘴前偏转90°所致。但是整体影响很小且没有影响可调音速喷嘴达到临界状态。

(a)L=0mm

(b)L=10mm图11 喉部附近马赫数分布Fig.11 Contour of mach number in the throat region
在无粘假设下,喷管的流量系数为[21]:
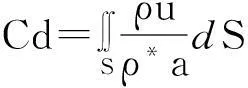
(9)
式中:S为节流面;ρ,u分别为当地的气体密度、流速;a,ρ*为声速和对应的临界密度。
对比节流面和音速线(Ma=1)可知,塞锥在0mm位置时实际的节流面积处大部分区域未达到临界状态,流速偏低。对比图11(a)与图11(b)并结合式(9)可知塞锥位置L=0mm的流量系数将较L=10mm的流量系数偏低。因此在设计塞锥时应该避免节流面位于塞锥顶尖位置。另外,节流面位于塞锥顶尖时还会导致塞锥顶尖附近的型面数据点过少(如图3)从而降低塞锥型面的精度。
3结论
通过两次包络线法方法设计了具有线性流量特性的可调音速喷嘴,并采用Fluent对线性可调音速喷嘴进行了三维数值仿真,对其临界反压比、流量特性和内部流场特性进行了研究。研究结果对可调音速喷嘴的设计具有指导意义。研究得到以下结论:
1)采用两次包络线方法设计的线性可调音速喷嘴流量调节过程中工作稳定,具有较好的线性流量特性。
2)可调音速喷嘴保持正常工作状态的临界反压比大于0.9,且临界反压比随流量减小而增大。
3)当节流面在塞锥顶尖位置时会显著降低可调音速喷嘴流量系数。当节流面不在塞锥顶尖位置时,可调音速喷嘴工作在不同流量时流量系数基本相同,约为0.963。
参考文献(References)
[1]Koupriyanov M, Etele J. Equivalence ratio and constriction effects on RBCC thrust augmentation [J]. Acta Astronautica, 2011, 68 (11/12):1839-1846.
[2]Olds J R, Saks G. A conceptual design tool for RBCC engine performance analysis [C]//Proceedings of 1997 Space Technology & Applications International Forum(STAIF-97), Albuquerque, NM, 1997.
[3]刘永兴, 王魁, 曹再勇. RBCC推进系统主火箭发动机气氧/煤油推力室研究 [J]. 火箭推进, 2009, 35 (6):23-26.
LIU Yongxing, WANG Kui, CAO Zaiyong. Investigation of GO2/kerosene thrust chamber of the main rocket engine for the RBCC propulsion system[J]. Journal of Rocket Propulsion, 2009, 35(6): 23-26.(in Chinese)
[4]马立坤. 燃气流量可调固体火箭冲压发动机动态响应过程研究 [D]. 长沙: 国防科学技术大学, 2011.
MA Likun. Investigation of the response process of variable flow ducted rocket[D]. Changsha: National University of Defence Technology, 2011. (in Chinese)
[5]李春辉, 彭晓峰, 李启明, 等. 微小流量测量音速喷嘴的流动特性 [J]. 热科学与技术, 2008, 7 (3):236-240.
LI Chunhui, PENG Xiaofeng,LI Qiming, et al. Flow characteristics of mini/micro sonic nozzles for micro-flow measurement[J]. Journal of Thermal Science and Technology, 2008, 7(3):236-240.(in Chinese)
[6]Cruz-Maya J A,Sánchez-Silva F, Quinto-Diez P. A new correlation to determine the discharge coefficient of a critical Venturi nozzle with turbulent boundary layer [J]. Flow Measurement and Instrumentation, 2006, 17 (5):258-266.
[7]Miralles B T. Preliminary considerations in the use of industrial sonic nozzles [J]. Flow Measurement and Instrumentation, 2000, 11 (4):345-350.
[8]Park K A. Effects of inlet shapes of critical venturi nozzles on discharge coefficients [J]. Flow Measurement and Instrumentation, 1995, 6 (1):15-19.
[9]Bignell N, Choi Y M. Thermal effects in small sonic nozzles[J]. Flow Measurement and Instrumentation, 2002, 13 (1/2):17-22.
[10]Li C H, Peng X F, Wang C. Influence of diffuser angle on discharge coefficient of sonic nozzles for flow-rate measurements [J]. Flow Measurement and Instrumentation, 2010, 21(4):531-537.
[11]Lim J M, Yoon B H, Oh Y K, et al. The humidity effect on air flow rates in a critical flow venturi nozzle [J]. Flow Measurement and Instrumentation, 2011, 22 (5):402-405.
[12]Wang C, Ding H B, Zhao Y K. Influence of wall roughness on discharge coefficient of sonic nozzles [J]. Flow Measurement and Instrumentation, 2014, 35:55-62.
[13]ASME PTC 19.5-2004. Flow measurement [S]. New York,USA: the American Society of Mechanical Engineers, 2005.
[14]Cao J Z, Zou X Z, Li H Z, et al. Characteristic analysis of laval nozzle in a fuel flow rate control valve at high temperature [J]. Hydromechatronics Engineering, 2012, 40(6): 48-53.
[15]D W Harvey. Throttling venturi valves for liquid rocket engines [C]//Proceedings of 6th Propulsion Joint Specialist Conference, AIAA-70-703, 1970.
[16]Dressier G A, Bauer J M. TRW pintle engine heritage and performance characteristics [C]// Proceedings of 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA-2000-3871, 2000.
[17]张育林. 变推力液体火箭发动机及其控制技术 [M]. 北京: 国防工业出版社, 2001.
ZHANG Yulin. Variable thrust liquid propellant rocket engine and its control techniques[M]. Beijing: National Defense Industry Press, 2001.(in Chinese)
[18]杨明, 安培文. 调节阀柱塞型阀芯形面数学模型推导[J]. 流体机械, 2009, 37 (10):34-37.
YANG Ming, AN Peiwen. Inferential reasoning on the mathematical model of valve plug of control valve[J]. Fluid Machinery, 2009, 37(10):34-37.(in Chinese)
[19]成鹏, 李清廉, 李春. 基于包络线法的调节阀阀芯型面改进设计方法 [J]. 流体机械, 2013, 41 (10):53-56.
CHENG Peng, LI Qinglian, LI Chun. Improved method for designing the contour of control valve plug based on the envelop method [J]. Fluid Machinery, 2013, 41 (10):53-56.(in Chinese)
[20]Zucrow M J, Holffman J D. Gas dynamics [M]. Toronto,Canada: John Wiley & Sons, 1977.
[21]Kliegel J R, Levine J N. Transonic flow in small throat radius of curvature nozzles[J]. AIAA Journal, 1969, 7(7): 1375-1378.
http://journal.nudt.edu.cn
Simulation on the performance of linear throttleable sonic nozzle
CHENGPeng,LIQinglian,ZHANGXinqiao,KANGZhongtao,CHENHuiyuan
(Science and Technology on Scramjet Laboratory, National University of Defense Technology, Changsha 410073, China)
Abstract:The mode transition of combined-cycle engine makes it necessary to throttle the mass flow rate of propellants continuously and stably. Aiming at gaseous propellant, a throttleable sonic nozzle was designed on the basis of normal sonic nozzle. The throttleable sonic nozzle achieves continuous throttling through a plug moving along axis. By adopting the twice-envelope method, the contour of the plug was designed to satisfy the linear characteristic of mass flow rate. Performances of the throttleable sonic nozzle were investigated through the numerical simulation of computational fluid dynamics. It is found that the mass flow rate is independent under the back pressure when the back pressure is lower than the critical back pressure and the critical back pressure ratio increases as mass flow rate decreases. The linear relationship between mass flow rate of linear throttleable sonic nozzle and location of plug was verified and results show that the discharge coefficient is high and hardly be affected by the location of plug.
Key words:throttleable sonic nozzle; linear; flow characteristic; mass flow rate throttling; back pressure
中图分类号:V435
文献标志码:A
文章编号:1001-2486(2015)06-048-06
作者简介:成鹏(1988—),男,湖南衡阳人,博士研究生,E-mail:imchengpeng@yeah.net;李清廉(通信作者),男,教授,博士,博士生导师,E-mail:peakdreamer@163.com
基金项目:新世纪优秀人才支持计划资助项目(NCET-13-0156)
收稿日期:*2014-12-11
doi:10.11887/j.cn.201506011

