外力对产生螺型位错的影响

段文山，张亚婕

(甘肃省原子分子物理与功能材料重点实验室，西北师范大学物理与电子工程学院,甘肃兰州　730070)

外力对产生螺型位错的影响

段文山，张亚婕

(甘肃省原子分子物理与功能材料重点实验室，西北师范大学物理与电子工程学院,甘肃兰州730070)

摘要：基于二维Frenkel-Kontorova模型,通过数值模拟,研究了在外驱动力作用下,交变力的频率和振幅对产生螺型位错的影响.结果表明，交变力的频率越低,振幅越大,越容易产生螺型位错.

关键词：螺型位错；FK模型；交变力；恒力

中图分类号：O 415

文献标志码：A

文章编号：1001-988Ⅹ(2015)03-0027-03

The effects of production of screw dislocations by the external forces

DUAN Wen-shan,ZHANG Ya-jie

(Key Laboratory of Atomic and Molecular Physics & Functional Materials of Gansu Province,

College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,Gansu,China)

Abstract:The effects of the frequencies and amplitudes of ac external driving forces on the production of screw dislocations by a two-dimensional(2D) Frenkel-Kontorova(FK) model are studied.The result shows it is very easy to produce the screw dislocation for lower frequencies and large amplitudes.

Key words:screw dislocations；FK modle；ac force；dc force

标准一维Frenkel-Kontorova(FK)模型[1-5]用于描述处于周期外势场中的一维原子链,相邻原子间的相互作用通过谐振势来描述.该模型最初用于描述位错中心附近的晶格运动[1].它既可以描述公度情况也可以描述非公度情况.当恒力和交变力作用在FK模型上,原子的固有频率和外加驱动力频率满足一定的关系时,就会出现动力学上的共振现象,即系统的平均速度呈现Shapiro台阶.近些年来,一些学者利用FK模型研究了外力作用下很多有趣现象[6-9],例如研究电荷密度波[10]、涡流晶体[11]、约瑟夫森结[12-16]和超导纳米[17,18]等.

当晶体在y方向受外加驱动力发生塑性变形时，在该方向会产生螺型位错.本文推广一维FK模型到二维FK模型，并借助二维FK模型研究外加驱动力对产生螺型位错的影响.

1模型

在FK模型中,采用六角形对称函数作为基底势函数,其形式为

(1)

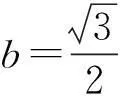
其中a为原子间的晶格常数，a=1.0，k0=1.0，λ=0.5.设该系统的每个原子的质量都是m=1,则所满足的动力学方程为

(2)

其中,F(t)=Fdc+Fac(t)为作用在每个原子的外加驱动力;恒力Fdc=Ay;交变力Fac(t)=Bsin(2πν0t)y;y为y方向的单位矢量；A为恒力振幅；B为交变力振幅；ν0为频率.

进行无量纲化,并用四阶龙格库塔法求解运动学方程(2).在数值模拟中,采用自由边界条件.取N×M=200×8,初始状态下体系的所有原子被固定在势能最低点.(2)式经过一个时间周期T=150.0使得系统达到一个平衡状态.

2计算结果及理论分析

基于以上模型,下面分别研究不同形式的外驱动力对螺型位错产生的影响.

2.1外驱动力的第一种形式

(3)

t0=100.0.图1a表示系统上层原子的初始状态,初始时刻上层平面的每个原子均匀的分布在下层周期势阱底.给上层左侧19列原子施加外驱动力F(t)后,看到左右两部分原子发生错动,即该系统左半部分原子相对于其余部分发生滑移,这就产生了螺型位错,如图1b所示.为了找出系统参量对螺型位错产生的影响,分别调节频率ν0、恒力振幅A和交变力振幅B给出对应的相图，如图2所示.

a 系统的初始状态；b 外力作用下系统产生螺型位错

首先取ν0为常量,看到A-B平面被分成两个不同区域，即出现螺型位错区域(AD)和不出现螺型位错区域(ND)，如图2a所示;其次取A为常量,看到随着ν0的增加,螺型位错越难产生如图2b所示;再次分别取B=3.0，10.0,看到当ν0较小时,容易产生螺型位错,但是随着ν0的增加,只有B较大时螺型位错更容易产生，如图2c，d所示.

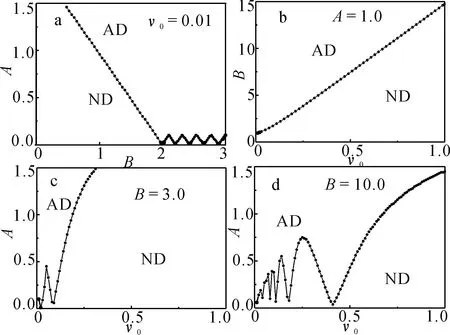
t0=100.0,AD表示产生螺型位错的区域,

2.2外驱动力的第二种形式

考虑外驱力的另一种形式

(3)

如图3所示,分别固定系统参量ν0,A,B.从图3a可以看出，当交变力的振幅大于某一临界值时，螺型位错很容易产生.与图2b比较,在图3b中也看到随着交变力频率增大,越来越难产生螺型位错.图3c，d说明当交变力的振幅较大时,更容易产生螺型位错.

2.3外驱动力的第三种形式

(4)

如图4,看到交变力的频率越低,振幅越大,越容易产生螺型位错.但是,在频率较大时,螺型位错很难产生.与图3b比较发现,当给系统加上一定的恒力时,更容易产生螺型位错.

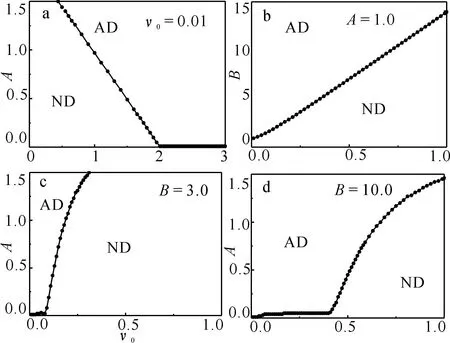
t0=100.0,n0=200

t0=100.0,n0=200

3结论

借助FK模型,研究了外驱动力作用下的二维弱阻尼系统中,交变力的频率和振幅对产生螺型位错的影响.数值模拟结果表明:① 交变力的频率ν0对系统产生螺型位错影响较明显,即ν0较小时,系统更容易产生螺型位错;② 交变力的振幅B对系统产生螺型位错影响较明显,即B较大时,系统更容易产生螺型位错.

参考文献：

[1]KONTOROVATA,FRENKELYI.OnthetheoryofplasticdeformationandtwinningⅠ[J].Zhurnal Eksperimental’noi i Teoreticheskoi Fiziki,1938,8:89-95.

[2]BRAUN O M,PCYRARD M.Ground state of the Frenkel-Kontorova model with a transverse degree of freedom[J].PhysicsReviewE,1995,51:4999-5005.

[3]XU H B ,WANG G R,CHEN S G. A generalized Frenkel-Kontorova model of the Ga/Si(112)dimerized overlayer system with vacancies[J].ChinesePhysics,2000,9:611-615.

[4]LI H B,ZHAO H,WANG Y H.The static properties of multi-chain Frenkel-Kontorova model:Ground state and static friction[J].PhysicsLettersA,2002,298:361-368.

[5]VANOSSI A,RODER J,BISHOP A R,et al.Underdamped commensurate dynamics in a driven Frenkel-Kontorova-type model[J].PhysicsReviewE,2003,67:016605-016610.

[6]INUI M,DONIACH S.Use of few-domain classical models to study mode locking in charge-density-wave systems[J].PhysicsReviewB,1987,35:6244-6250.

[7]FLORIA L M,FALO F.Shapiro steps in the steady-state dynamics of incommensurate structures[J].PhysicsReviewLetters,1992,68:2713-2716.

[8]FALO F,FLORIA L M,MARTINEZ P J,et al.Unlocking mechanism in the ac dynamics of the Frenkel-Kontorova model[J].PhysicsReviewB,1993,48:7434-7442.

[9]FLORIA L M,MAZO J J.Dissipative dynamics of the Frenkel-Kontorova model[J].AdvancedPhysics,1996,45(6):505-598.

[10]GRUNER G.The dynamics of charge-density waves[J].ReviewsofModernPhysics,1988,60:1129-1138.

[11]KOLTON A B,DOMINGUEZ D,GRONBECH-JENSEN N.Mode locking in ac-driven vortex lattices with random pinning[J].PhysicsReviewLetters,2001,86:4112-4115.

[12]JOSEPHSON D.Supercurrents through barriers[J].AdvancedPhysics,1965,14:419-451.

[13]SHAPIRO S J.Currents in superconducting tunneling:The effect of microwaves and other observations[J].PhysicsReviewLetters,1963,11:80-83.

[14]KOMISSINSKIY P,OVSYANNIKOV G A,CONSTANTINIAN K Y,et al.High-frequency dynamics of hybrid oxide Josephson heterostructures[J].PhysicsReviewB,2008,78:024501-024508.

[16]BENZ S P,RZCHOWSKI M S,TINKHAM M,et al.Fractional giant Shapiro steps and spatially correlated phase motion in 2D Josephson arrays[J].PhysicsReviewLetters,1990,64:693-696.

[17]BAE M H,DINSMORE Ⅲ R C,AREF T,et al.Current-phase relationship,thermal and quantum phase slips in superconducting nanowires made on a scaffold created using adhesive tape[J].NanoLetters,2009,9(5):1889-1896.

[18]DINSMORE III R C,BAE M H,BEZRYADIN A.Fractional order Shapiro steps in superconducting nanowires[J].AppliedPhysicsLetters,2008,93:192505-192509.

(责任编辑孙对兄)

作者简介：段文山(1962—)，男，甘肃民勤人，教授，博士，博士研究生导师．主要研究方向为非线性物理．

基金项目:国家自然科学基金资助项目(11275156)

收稿日期：2014-10-20;修改稿收到日期:2015-01-03

E-mail:duanws@nwnu.edu.cn