基于隐空间的低秩稀疏子空间聚类

刘建华

(浙江工商职业技术学院电子与信息工程学院，浙江宁波　315012)

基于隐空间的低秩稀疏子空间聚类

刘建华

(浙江工商职业技术学院电子与信息工程学院，浙江宁波315012)

摘要：提出了一种基于隐空间的低秩稀疏子空间聚类算法，在聚类的过程中可以对高维数据进行降维，同时在低维空间中利用稀疏表示和低秩表示对数据进行聚类，大大降低了算法的时间复杂度.在运动分割和人脸聚类问题上的实验证明了算法的有效性.

关键词：子空间聚类；稀疏表示；低秩表示；运动分割；人脸聚类

中图分类号：TP 391

文献标志码：A

文章编号：1001-988Ⅹ(2015)03-0049-05

Low-rank sparse subspace clustering in latent space

LIU Jian-Hua

(College of Electronics and Information Engineering,Zhejiang Business Technology Institute,

Ningbo 315012,Zhejiang,China)

Abstract:This paper proposed a novel algorithm named low-rank sparse subspace clustering in latent space(LatLRSSC),it can reduce the dimension and cluster the data lying in a union of subspaces simultaneously.The main advatages of our method is that it is computationally efficient.The effectiveness of the algorithm is demonstrated through experiments on motion segmentation and face clustering.

Key words:subspace clustering;sparse representation;low-rank representation;motion segmentation;face clustering

0引言

过去的几十年人们见证了数据的爆炸式增长，这对于数据的处理工作提出了巨大的挑战，特别是这些数据集通常都是高维数据.数据的高维特性不仅增加了计算时间，而且由于噪声和环境空间降低了算法的性能.实际上，这些数据的内在尺度往往比实际空间中小得多，这就促使人们运用一些技术发现高维数据的低维表示，比如低秩近似和稀疏表示等[1-3].实际上，在许多问题中，高维空间中的数据往往可以用低维子空间进行表示.子空间聚类算法就是挖掘数据低维子空间的一种聚类算法[4]，它已经被广泛地应用在许多领域，如计算机视觉中的运动分割和人脸聚类，控制领域的混合系统辨识，社交网络中的社区集群.为了解决高维数据聚类问题，目前已经提出了很多聚类算法，如混合高斯模型、NMF和一些代数方法(如k-subspace)、混合概率主成分分析(MPPCA)、多阶段学习与RANSAC.这些方法取得了一定的效果，但是还有很多局限性，如计算复杂度太高，对噪音敏感等.

最近，利用稀疏表示和低秩表示进行子空间聚类的研究得到了广泛的关注，研究人员提出了一系列相关的新型子空间聚类算法，如稀疏子空间聚类(SSC)[5,6]、低秩表示(LRR)[4,7]、低秩子空间聚类(LRSC)[8]和低秩稀疏子空间聚类(LRSSC)[9]，这些方法的本质是每一个数据点可以通过其他数据点稀疏表示或者低秩表示得到.尽管稀疏子空间聚类(SSC)和低秩表示(LRR)取得了巨大的成功，仍然有很多问题没有解决.特别是稀疏表示和低秩表示的计算复杂度相当高，尤其是当数据的维数很高的时候[6].为了解决这个问题，通常的做法是在应用这类聚类算法之前对数据进行降维预处理.一些降维方法如主成分分析(PCA)或者随机投影(RP)可以有效降低数据维数.然而，一个良好学习的投影矩阵可以在更低的数据维度上得到更好的聚类效果.基于低维隐空间的稀疏表示已经有学者提出了一些方法[10,11]，但是这些方法都是为分类问题进行设计，而非针对聚类问题.

基于上述问题，文中提出一种基于低维隐空间的低秩稀疏子空间聚类方法(LatLRSSC)，在数据降维的同时，发掘数据的稀疏和低秩表示.首先算法学习得到数据从原始空间到低维隐空间的变换矩阵，同时在这个低维的隐空间中得到数据的稀疏和低秩系数，最后利用谱聚类算法对数据样本进行分割.为了验证文中提出方法的有效性，分别在HOPKINS 155 数据集和extended Yale B 数据集上进行运动分割和人脸聚类的实验，实验结果表明，文中提出的LatLRSSC算法具有较好的聚类性能.

1相关工作

1.1稀疏子空间聚类

根据文献[5,6]，每一个数据点可以表示为其他数据点的稀疏线性组合，通过这些稀疏系数构造清河矩阵进行子空间聚类.也就是说，给定一个数据集X，希望找到一个系数矩阵C，满足X=XC并且diag(C)=0.可以通过求解(1)式得到解.

(1)

当数据集被噪声G污染时，SSC算法假设每个数据点可以表示为X=XC+G,可以通过求解凸优化问题(2)得到解.

(2)

1.2低秩表示(LRR)

低秩表示(LRR)算法和稀疏子空间聚类(SSC)算法非常类似，区别在于LRR算法的目标是寻找数据的低秩表示，而SSC算法在于寻找数据的稀疏表示.LRR通过求解凸优化问题(3)得到解.

(3)

当数据集被噪声G污染时，LRR通过求解凸优化问题(4)得到解.

(4)

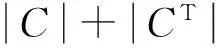
2基于低维隐空间的低秩稀疏子空间聚类

不同于传统的稀疏子空间聚类算法(SSC)和低秩表示(LRR)，文中将数据映射到一个低维的隐空间中，同时在这个低维空间中寻求数据的低秩稀疏系数.令P∈Rt×D为一个线性变换矩阵，它将数据从原始空间RD映射到一个维数为t的隐空间中.通过目标函数的最小化，可以同时得到变换矩阵和数据集的低秩稀疏系数:

(5)

其中

(6)

(6)式的第一项为求取数据集的低秩系数;第二项为求取数据集的稀疏系数;第三项的主要目的是去除噪声影响;最后一项是类似于PCA的正则项，主要目的是保证映射变换不能过多丢失一些原始空间的信息;λ1和λ2为非负常数.另外，要求P正交并且归一化，这样就避免了解的退化，并且保证了优化方法的计算效率.

可以注意到，(6)式是能够进行扩展的，这样就可以对位于仿射子空间中的数据进行处理.可以对优化问题(5)增加一个约束条件得到

(7)

2.1优化问题求解

根据上面的定义，有下面的命题.

命题1优化问题(5)存在一个最优化的解P*，对于某些Ψ∈RN×t，N为数据样本数，P*具有以下形式

直观上， 命题1是说投影变换可以写成数据样本的一个线性组合.文献[12]中，这个形式已经被应用在字典学习的框架中.

基于命题1，目标函数(6)可以写为

(8)

其中K=YTY.约束条件变为

(9)

所以，优化问题(5)可表示为

(10)

其中

这样，可分别通过Ψ和C来求解这个优化问题.

2.2Ψ的优化步骤

首先固定C，目标函数就变为

(11)

上式可以另写为

(12)

其中Q=ΨΨT∈RN×N.由约束条件ΨTKΨ=I可得到新的约束条件ΨΨTKΨΨT=ΨΨT或者QKQT=Q,目标函数(12)可以进一步简化为

(13)

使用同样的约束条件，并且知tr(K)为一个常数,利用K=VSVT的特征值分解，得到

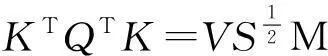
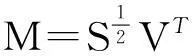
利用ΨTKΨ=MTM和变换

得到等价于问题(11)的优化问题:

(14)

优化问题(14)就是经典的最小特征值问题.它的解就是与Δ的前l个最小特征值相关联的l个特征向量.一旦得到了最优的M*，那么最优的Ψ*就可以利用(5)式得到:

(15)

2.3C的优化步骤

固定Ψ，通过求解下列优化问题来得到C

(16)

其中 B=ΨTK.

接下来，推导了一个解决优化问题(16)的有效方法.在ADMM框架下，引入两个辅助变量C=C1=C2来区分两个不同的范数，引入J来保证每一步都得到闭合解:

则增广拉格朗日方程为

其中μ1和μ2为可调参数.每一步中，通过分别求解J,C1和C2的梯度，更新对偶变量Λ1和Λ2，可以得到ADMM每一步的迭代公式.

(17)

(18)

Λ1和Λ2的更新规则如下:

3实验

分别验证文中提出的LatLRSSC算法在运动分割和人脸聚类两种问题上的性能.对于运动分割问题，采用Hopkins155数据集，包含155个视屏序列.对于人脸聚类问题，采用ExtendedYaleB数据集，包含38类人脸图像数据.

实验中，采用聚类错误率来评价聚类算法的性能：

对比算法采用了LRR，LRSC，SSC和LRSSC这4种应用较为广泛的子空间聚类算法.

3.1运动分割实验

运动分割是指从视频序列中对于不同的刚体运动提取一组二维点轨迹，对这些轨迹进行聚类，实现不同运动物体的分割.这里，数据集X为2F×N维，其中N为二维轨迹的数目，F为视频的帧数.在仿射投影模型中，这些与刚体运动相关联的二维轨迹位于维数为1,2或3的仿射子空间R2F中.

实验中，采用Hopkins155运动分割数据集，其中120个视频序列由2个运动构成，35个视频序列由3个运动构成.平均来说，每一个包含2个运动的视频序列包含N=256个特征轨迹和F=30帧画面，而每一个包含3个运动的视频序列包含N=398个特征轨迹和F=29帧画面.对于每一个视频序列，这些二维轨迹通过跟踪器自动提取，并且噪音点已经手动去除.

表1比较了不同算法在Hopkins155数据集上的聚类表现.实验中，除了文中提出的算法，对于其他算法，利用PCA进行预处理，将数据集降维到4n维(n为子空间数目).

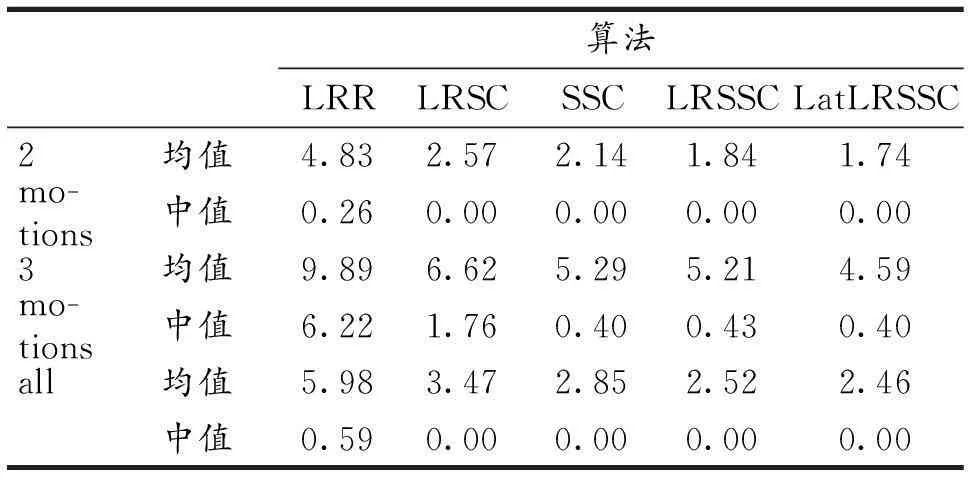
表1　不同聚类算法在Hopkins 155数据集上的

从表1 可以看出，对于2个或3个运动，文中提出的算法LatLRSSC相较于其他4种方法具有较好的聚类性能，说明LatLRSSC对于运动分割问题具有很好的效果.对比其他算法可知，相对于直接采用PCA进行降维操作，LatLRSSC通过对数据集的学习能够得到更加合理的映射矩阵.

3.2人脸聚类实验

给定多个人在同一角度、不同光照的人脸图像，希望将不同的人脸图像划分开来(图1).在Lambertian假设下，物体图像在固定角度、不同光照条件下位于一个近似的9维子空间中，因此，采集的多个人的人脸图像也位于这样的9维子空间中.

图1　人脸图像聚类示例

采用Extended Yale B数据集，数据集包含n=38个人的人脸图像(192×168像素)，每个人有Ni=64张在不同光照条件下的正面图像.为了降低计算成本和存储代价，将每幅人脸图像采样到48×42像素，并将图像向量化为2 016维，因此维度D=2 016.实验中，除了文中提出的算法，对于其他算法，依然利用PCA进行降维预处理.

为了研究这些算法对不同聚类数目的聚类性能，将38类人脸分成4组，前3组分别包含1～10,11～20,21～30个人的人脸图像，第四组包含31～38个人的人脸图像.对于前3组，取n∈{2,3,5,8,10}；对最后一组，取n∈{2,3,5,8}.实验结果如表2所示.

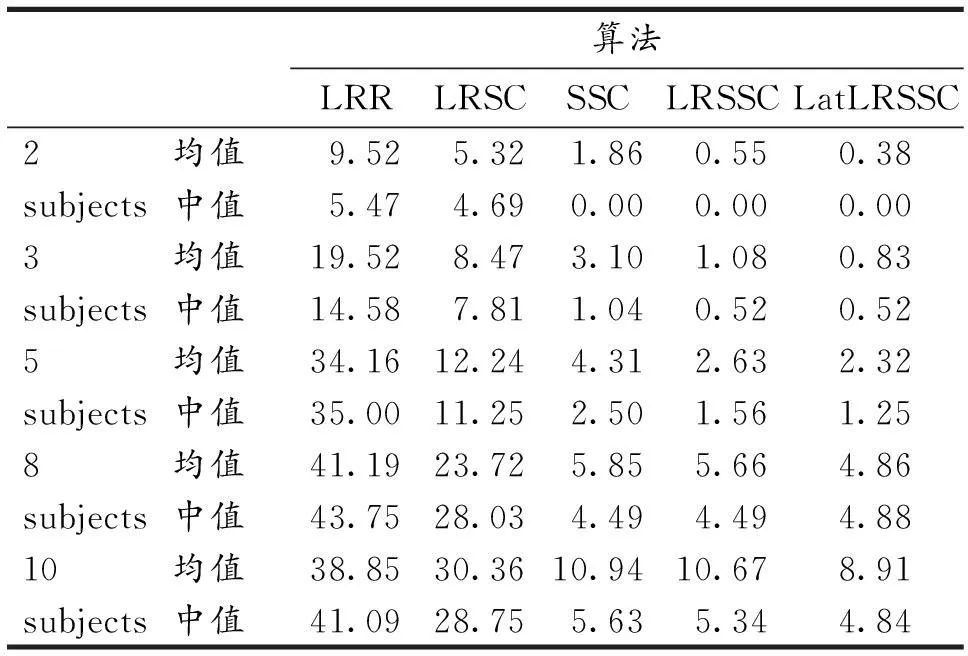
表2　不同算法在Extended Yale B 数据集上的

从表2可以看出，文中提出的LatLRSSC对不同的聚类数目均得到了更低的聚类错误率，说明了该算法优于其他算法.

4结束语

文中提出了一种基于隐空间的低秩稀疏子空间聚类算法.本算法是稀疏子空间聚类和低秩表示的一种扩展，该算法在聚类的过程中可以对高维数据进行降维，同时在低维空间中利用稀疏表示和低秩表示对数据进行聚类.在运动分割和人脸聚类上的实验表明，该算法具有很好的聚类性能.

与大多数子空间聚类算法一样，文中假设子空间是线性的，如何将本算法在非线性子空间上进行扩展是接下来需要继续研究的工作.

参考文献:

[1]ABDI H,WILLIAMS L J.Principal component analysis[J].WileyInterdisciplinaryReviews:ComputationalStatistics,2010,2(4):433-459.

[2]LAUERF,SCHNORRC.Spectralclusteringoflinearsubspacesformotionsegmentation[C]//Proceedings of the 12 th International Conference on Computer Vision.Kyoto:IEEE,2009:678-685.

[3]WRIGHTJ,YANGAY,GANESHA,etal.Robustfacerecognitionviasparserepresentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2):210-227.

[4]LIUG,LINZ,YUY.Robustsubspacesegmentationbylow-rankrepresentation[C]//Proceedings of the 27th International Conference on Machine Learning.Haifa:Omnipress,2010:663-670.

[5]ELHAMIFARE,VIDALR.Sparsesubspaceclustering[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Anchorage:IEEE,2009:2790-2792.

[6]ELHAMIFAR,VIDALR.Sparsesubspaceclustering:Algorithm,theory,andapplications[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(11):2765-2781.

[7]LIUG,LINZ,YANS.Robustrecoveryofsubspacestructuresbylow-rankrepresentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(1):171-184.

[8]FAVAROP,VIDALR,RAVICHANDRANA.Aclosedformsolutiontorobustsubspaceestimationandclustering[C]//Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition.Colorado:IEEE,2011:1801-1807.

[9]WANGYX,XUH,LENGC.Provablesubspaceclustering:WhenLRRmeetsSSC[C]//Advances in Neural Information Processing Systems.Nevada:MITPress,2013:64-72.

[10]MAIRALJ,BACHF,PONCEJTask-drivendictionarylearning[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(4):791-804.

[11]NGUYENHV,PATELVM,NASRABADINM,etal.Sparseembedding:Aframeworkforsparsitypromotingdimensionalityreduction[M]//Computer Vision—ECCV 2012.Berlin:Springer,2012:414-427.

[12]RUBINSTEINR,ZIBULEVSKYM,ELADM.Doublesparsity:Learningsparsedictionariesforsparsesignalapproximation[J].IEEE Transactions on Signal Processing,2010,58(3):1553-1564.

(责任编辑惠松骐)

作者简介：刘建华(1979—)，男，江西九江人，讲师，硕士.主要研究方向为模式识别与图像处理.

基金项目:浙江省自然科学基金资助项目(LY14F020009)

收稿日期：2015-01-19;修改稿收到日期:2015-03-24

E-mail:liujianhua_1979@126.com