考虑连锁故障的大电网可靠性评估

孙志媛，李海波，鲁宗相

(1.广西电网有限责任公司 电力科学研究院，广西 南宁 530023;2.清华大学电机系 电力系统国家重点实验室，北京 100084)

电力系统可靠性是对电力系统按可接受的质量标准和所需数量不间断地向电力用户供应电力和电能量能力的度量［1］，可靠性评估对于电网规划和运行有着十分重要的指导意义。近年来，巴西［2］、印度［3］、美墨［4］等一系列大停电事件的发生造成了巨大的经济损失和社会影响，从而引起了电力工作者对电力系统可靠性评估的高度重视。

国外对电力系统可靠性的研究工作开展较早，1969年R.Billinton教授即发表了第1篇论文，随后提出了可靠性测试标准系统［5］，为电力系统可靠性研究奠定了重要基础。随后大量学者投入到了电力系统可靠性研究领域中，从计算精度、速度及在电网规划运行中的应用等方面进行了大量研究，取得了丰硕成果。但是传统可靠性研究仅关注元件的独立故障，不考虑元件间故障的相关性，这样得出的结论是电网发生严重事故的概率极低，几乎不可能发生。而部分学者在对北美电网事故数据的统计分析中却发现，大停电事故规模与其发生概率呈现幂指数率(power law)［6－7］，这表明大停电事故的风险是存在的。为了克服传统可靠性的弊端，众多学者开始研究电网复杂性理论以及实际电网的连锁故障模型及停电机理，证明了电网具有自组织临界性，并提出了多种模型用来模拟系统连锁故障和电网演化过程［8－11］，如:OPA模型、CASCADE模型、分支过程模型等。但是，这些研究仅关注电网的连锁故障事故，没有将其融入到电力系统可靠性评估框架中，形成完整的评估体系。

考虑到上述不足，笔者基于元件连锁故障评估模型和传统发输电系统可靠性评估算法，提出考虑元件连锁故障的电力系统可靠性评估算法。在元件连锁停运模型中，考虑节点电压、线路潮流对线路故障率的影响［12］，采用直流最优潮流计算最小切负荷量，并将这些算法融入到传统电力系统可靠性评估流程中，计算结果既能反映电网的“高概率低后果”(High Probability Low Impact，HPLI)事件，也能反映传统算法无法体现的“低概率严重后果”(High Impact Low Probability，HILP)事件。

1 元件连锁停运模型

在实际运行中，电力系统元件发生故障的原因多种多样［12］，归纳起来主要有4类:①元件不正常运行时导致元件保护装置动作;②元件本身故障，例如制造缺陷、部件老化、设备发热、绝缘损坏等;③外界环境，如雷击、台风、暴雪、冰雹等恶劣天气;④人为误操作导致元件保护误动作等。综上所述，可知元件故障率主要由静态故障率和运行条件相依的故障率增量构成，即

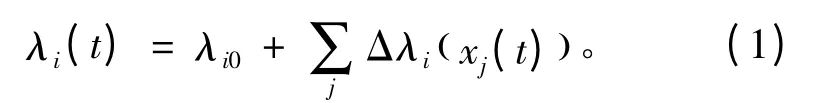
式中 λi(t)为元件i在时刻t的故障率;λi0为元件的静态故障率，即元件的多年统计故障率数据;Δλi为条件相依的故障率增量，其中xj(t)为因素j(如功率、电压等)在时刻t的物理量。

该文选取对元件故障率影响较大的电压、线路有功潮流作为变量修正元件的故障率。如果节点电压过高或过低，则与该节点相连的线路会跳闸，因此，线路故障率与节点电压有较强的相关性，其电压相依故障率增量与电压的关系如图1所示。

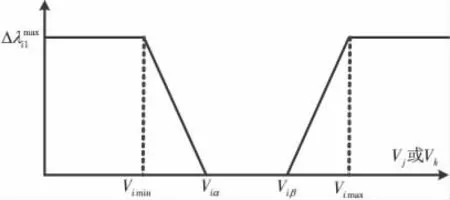
图1 电压相依故障率增量与节点电压的关系Figure 1 Relationship between the voltage-dependent failure rate and voltage

线路故障率与其经过的潮流也有明显的相关性，在较低的潮流水平下，线路故障率水平与静态故障率相同，随着线路潮流的增加(超过某阈值后)，线路由于发热、过载等原因，线路故障率会明显增加，其潮流相依故障率增量与潮流的关系如图2所示。

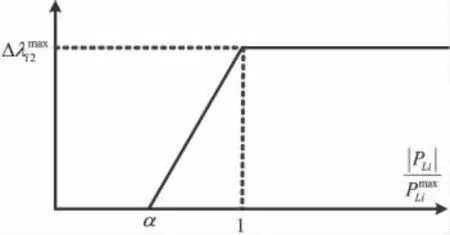
图2 潮流相依故障率增量与线路潮流的关系Figure 2 Relationship between the power flow-dependent failure rate and power flow

对于线路i(i=1，2，…，nL)，其故障率增量可表示为

其中，Δλi1和Δλi2分别表示电压相依故障率增量和潮流相依故障率增量，其余各参数含义参见图1，2。

为了模拟电网的连锁故障情况，笔者提出元件连锁停运模拟算法，其基本流程如下。

1)根据系统数据，计算初始交流潮流，并根据各节点电压、线路潮流，修正各线路的故障率;

2)生成随机数，对各线路进行抽样，得到电网元件故障集合;

3)计算最优切负荷量，为了提高计算效率，切负荷程序采用DC潮流，其优化模型为

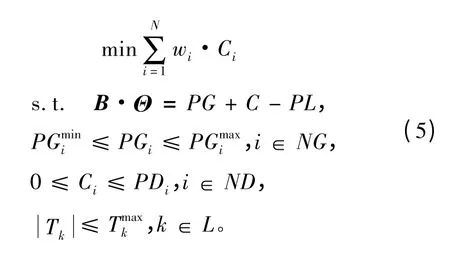
式中 B为节点导纳矩阵;Θ是节点电角度向量;PG，PL和C分别为发电机有功输出、负荷需求和切负荷量分别代表机组i最小和最大出力;PDi是节点i的负荷量;Tk是线路k的潮流，是其功率上限;

4)针对切负荷后的电网，重新计算交流潮流，根据各节点电压、线路潮流，生成随机数，并重新对各线路进行抽样，若抽样到新的线路故障，则转至步骤3进行最优切负荷计算;若没有新的元件故障，则模拟过程结束。模拟算法的流程框图如图3所示。

图3 元件连锁故障模拟流程示意Figure 3 Flowchart of the cascading simulation

2 电力系统可靠性评估及指标体系

在元件连锁停运模型的基础上，运用统计学方法，对多次模拟结果进行统计分析，最终得到系统综合可靠性指标，其模拟流程如下

1)根据输入系统数据，运行连锁故障模拟算法，得到系统状态S;

2)根据系统状态S，判断系统是否需要削减负荷以及最优切负荷量，若无切负荷，则转至步骤1;若有切负荷，则转至步骤3;

该文采用5个经典可靠性指标［13］:①切负荷概率LOLP，为系统年停电总时间与8 760的比值，无量纲;②切负荷频率LOLF，为系统年停电事件发生的次数，次/年;③平均切负荷持续时间LOLD，为系统平均每次停电的持续时间，h/次;④缺供电量EENS，为系统由于停电事件导致的年停电电量之和，GW·h/年;⑤系统分SI，为系统在最大负荷情况下，年停电分钟数，min。

3 算例分析

基于IEEE-RTS79系统进行仿真计算，运用该文提出的连锁停运模型计算，与不考虑连锁故障的传统算法结果进行对比，验证该文模型的合理性和正确性;针对广西电网2016年规划方案进行计算分析，为电网规划和运行提供指导。

3.1 IEEE-RTS79系统

IEEE-RTS79系统结构如图4所示，共有24条母线，38条支路，34台发电机，其装机容量为3 405 MW，年最大负荷为2 850 MW，取Vimin=0.95，Viα=0.98，Viβ=1.02，Vimax=1.05(标幺值)，α=0.85，ε=0.01，可得到传统可靠性评估结果［14］和基于该文提出的考虑连锁故障下的可靠性评估结果，如表1所示;模拟的故障重数分布如表2所示(模拟次数为10 000次)。

通过表1，2计算结果可知，考虑连锁故障的可靠性指标要比不考虑连锁故障的结果偏大，主要原因是考虑连锁故障后，电网的高重故障数量增加。仅考虑独立故障时，最高仅能抽样到2重故障，并且仅抽样到0.02%的2重故障与实际经验不符;若考虑连锁故障时，最高能够抽样到6重故障，并且2重故障的概率明显增加，接近1%。

如图5所示，可以看出，考虑连锁故障的事故规模概率分布较为分散，能够反映出系统大规模故障(损失负荷20%以上)的概率分布，而传统的方法无法反映大规模故障，仅能模拟到损失负荷18%以下的事件情况。

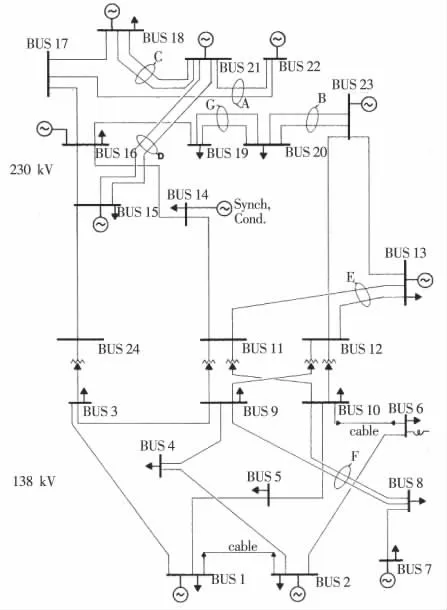
图4 IEEE-RTS79系统结构示意Figure 4 The schematic diagram of IEEE-RTS79 system

表1 该文算法和传统算法的可靠性评估结果对比Table 1 Comparison of the reliability indices between the conventional results and the proposed method

表2 该文算法和传统算法的故障重数模拟对比Table 2 Comparison of the failure modes between the conventional results and the proposed method

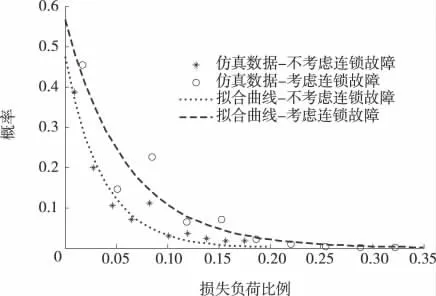
图5 连锁故障前、后的系统事故规模概率分布Figure 5 Probability distribution of system accident before and after cascading failure

3.2 广西电网2016年规划方案

以广西电网2016年规划方案为基础，计算其丰大运行方式下的可靠性指标。广西电网2016年规划方案负荷预测为35 627 MW，开机+备用容量为37 200 MW，共有110 kV及以上线路1 374条，母线923条。

参数同3.1节算例，分别计算不考虑连锁故障和考虑连锁故障2种情况，计算结果如表3所示;模拟到的故障重数分布如表4所示(模拟次数为10 000次)。

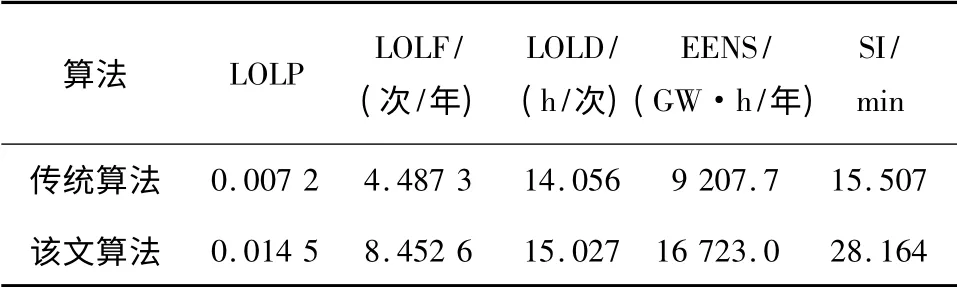
表3 该文算法和传统算法的可靠性评估结果对比Table 3 Comparison of the reliability indices between the conventional results and the proposed method

表4 该文算法和传统算法的故障重数模拟对比Table 4 Comparison of the failure modes between the conventional results and the proposed method

根据仿真结果，广西电网2016规划方案不同事故规模(损失负荷比例范围0.87%～33.46%)的概率密度分布如图6所示。

根据模拟结果，可得到广西电网2016年规划方案发生小规模停电事件(损失负荷1%左右)的概率为0.039 5，属于HPLI事件;发生大规模停电事件(损失负荷30%及以上)的概率为0.000 1(对应故障重数分布的7重故障)，属于HILP事件。

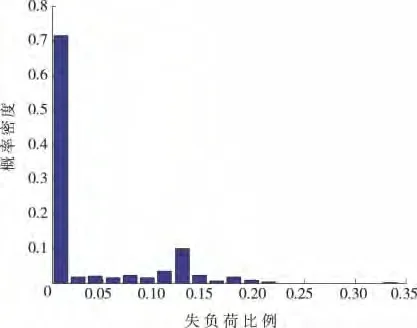
图6 广西电网2016年规划方案结构示意Figure 6 Schematic diagram of Guangxi power grid＇s planning scheme in 2016

4 结语

笔者基于电压、潮流对于线路故障率的影响机理，提出了元件连锁故障模型，并将其应用到发输电组合系统可靠性评估中，该方法优点有①采用交直流潮流交叉计算方法，利用直流最优潮流计算最少切负荷量，交流潮流计算节点电压、线路潮流，用来修正线路故障率，可大大提高计算效率;②将连锁故障模型融入到大电网可靠性评估模型中，避免了传统方法仅能抽样独立故障的缺陷，完善了可靠性评估算法;③仍然沿用了传统可靠性指标体系，能够实现与传统算法的兼容，指标计算结果便于指导电网规划、运行等。

通过对IEEE-RTS79系统及广西电网2016年规划方案的计算分析，可得出结论。

1)笔者提出的连锁故障模拟算法能够有效模拟到系统的高重故障，最高能够抽样到6重故障，并且2重故障的概率明显增加，接近1%;

2)考虑连锁故障的事故规模概率分布较为分散，能够反映出系统大规模故障(损失负荷20%以上)的概率分布，而传统的方法无法反映大规模故障，仅能模拟到损失负荷18%以下的事件情况。

3)广西电网2016年规划方案发生小规模停电事件(损失负荷1%左右)的概率为0.039 5，属于HPLI事件;发生大规模停电事件(损失负荷30%及以上)的概率为0.000 1(对应故障重数分布的7重故障)，属于HILP事件。

［1］文福拴，吉兴全，王钦.电力工业改革对电力系统可靠性的影响［J］.电力科学与技术学报，2007，22(3):1-11.WEN Fu-shuan，JI Xing-quan，WANG Qin.Influence of electric power industry reform on system reliability［J］.Journal of Electric Power Science and Technology，2007，22(3):1-11.

［2］陈亦平，洪军.巴西“11·10”大停电原因分析及对我国南方电网的启示［J］.电网技术，2010，34(5):77-82.CHEN Yi-ping，HONGJun.Analysis on causes of blackout occurred in Brazilian power grid on Nov.11，2009 and lessons drawn from it to China Southern Power Grid［J］.Power System Technology，2010，34(5):77-82.

［3］汤涌，卜广全，易俊.印度“7·30”、“7·31”大停电事故分析及启示［J］.中国电机工程学报，2012，32(25):167-174.TANG Yong，BU Guang-quan，YI Jun.Analysis and lessons of the blackout in indian power grid on July 30 and 31，2012［J］.Proceedings of the CSEE，2012，32(25):167-174.

［4］毛安家，张戈力，吕跃春，等.2011年9月8日美墨大停电事故的分析及其对我国电力调度运行管理的启示［J］.电网技术，2012，36(4):74-78.MAO An-jia，ZHANG Ge-li，LV Yue-chun，et al.Analysis on large-scale blackout occurred in South America and North Mexico interconnected power grid on Sept.8，2011 and lessons for electric power dispatching in China［J］.Power System Technology，2012，36(4):74-78.

［5］IEEE RTSTask Force of APM Subcommittee.IEEE reliability test system［J］.IEEE Transaction on PAS，1979，98(6):2 047-2 054.

［6］Carreras B A，Newman D E，Dobson I，et al.Initial evidence for self-organized criticality in electric power blackouts［C］.Proceedings of 33rd Hawaii International Conference on System Sciences，Maui，Hawaii，2000.

［7］林涛，范杏元，徐遐龄.电力系统脆弱性评估方法研究综述［J］.电力科学与技术学报，2010，25(4):20-24.LIN Tao，FAN Xing-yuan，XU Xia-ling.Summary of power system vulnerability assessment methods［J］.Journal of Electric Power Science and Technology，2010，25(4):20-24.

［8］Dobson I，Carreras B A，Newman D E.A probabilistic loading-dependent model of cascading failure and possible implication for blackouts［C］.Proceedings of 34th Hawaii International Conference on System Sciences，Maui，Hawaii，2003.

［9］Dobson I，Carreras B A，Newman D E.A branching process approximation to cascading load-dependent system failure［C］.Proceedings of 34th Hawaii International Conference on System Sciences，Maui，Hawaii，2004.

［10］陈亦平，赵曼勇，刘文涛，等.南方电网连锁故障风险分析及防御措施研究［J］.南方电网技术，2010，4(3):8-11.CHEN Yi-ping，ZHAO Man-yong，LIU Wen-tao，et al.The risks analysis and defensive measures research of cascading failures in China Southern Power Grid［J］.Southern Power System Technology，2010，4(3):8-11.

［11］胡澜.考虑连锁故障影响的检修优化［J］.电力科学与技术学报，2010，25(4):96-100 HU Lan.Maintenance optimization with cascading failures influence considering［J］.Journal of Electric Power Science and Technology，2010，25(4):96-100.

［12］刘海涛，程林，孙元章，等.基于实时运行条件的元件停运因素分析与停运率建模［J］.电力系统自动化，2007，31(7):6-11.LIU Hai-tao，CHENG Lin，SUN Yuan-zhang，et al.Outage factors analysis and outage rate model of components based on operating conditions［J］.Automation of Electric Power Systems，2007，31(7):6-11.

［13］Billinton R，Li Wenyuan.Reliability assessment of electric power systems using monte carlo methods［M］.New York and London:Plenum Press，1994.

［14］Billinton R，Li W.A system state transition sampling method for composite system reliability evaluation［J］.IEEE Transactions on Power Systems，1993，8(3):761-770.