基于条件风险方法的含风电系统旋转备用优化调度

周任军，张 浩，范文帅，邓学华

(1.长沙理工大学 智能电网运行与控制湖南省重点实验室，湖南 长沙 410004;2.中国能源建设集团有限公司 湖南省电力勘测设计院，湖南 长沙 410007)

为应对负荷预测偏差和发电机故障停运等不确定性因素的影响，电力系统通常需要预留一定的旋转备用容量来保证其安全稳定运行。传统的旋转备用一般通过确定性方法求得，如取系统负荷或总装机容量的固定比例，也可取系统中单机最大容量，这些方法应用广泛，计算简单，但其经济性并不理想［1］，且较少考虑不确定随机因素对旋转备用总量的影响。随着风电场并网规模日益增大，且风电出力预测困难，传统的备用容量确定方法已不足以解决系统安全稳定运行的问题。

文献［2］以旋转备用购买成本最小为目标，其模型中计及了发电机组故障停运和负荷误差;文献［3］以系统发电成本和期望停电成本最小为目标，兼顾了风电出力偏差对系统运行可靠性和经济性的影响，求解出系统所需的最优旋转备用;文献［4］改变了传统模型中旋转备用容量采取确定性方法获取的方式，采用机会约束规划法，设定获取的备用容量满足系统要求的概率大于一定的置信水平;文献［5］研究了旋转备用分配方案对系统可靠性和经济成本的影响，提出了基于成本和风险的旋转备用分配方法;文献［6］的目标函数中计及了发电成本和备用成本，通过引入正、负旋转备用约束来应对风电功率预测误差带来的影响，通过确定性方法求得结果。以上方法或者没有考虑到非常规机组的随机性，或者用进化规划处理随机性问题，对不确定性因素引起的风险度量缺少刻画，或者度量风险中未考虑置信水平以外的尾部风险。

笔者引入条件风险价值CVaR(Conditional Value-at-Risk)求解系统旋转备用容量。条件风险价值作为目前广泛应用的一种风险度量工具，主要用于处理经济学中的各类随机性问题，在电力系统中的研究一般集中在电力市场方面［7－8］，其实质仍是属于经济领域和市场范畴的风险计量方法，将条件风险价值引申至电力系统技术研究范围还不多见［9］。笔者通过其在处理随机性问题中良好的数学特性来应对电力系统中风电出力不确定性因素的影响，用以解决具有随机性特点的系统旋转备用问题，建立新的旋转备用约束模型。在确定系统所需备用大小的同时，也直观描述系统获取的风险水平，便于决策者根据不同情况在经济性和可靠性之间进行度量分析。

1 考虑旋转备用的系统调度模型

1.1 目标函数

1)发电成本函数。

系统经济调度的目标函数为常规机组的发电成本，其表达式为

式中 ai，bi，ci为常规机组i的发电成本系数为常规机组i输出的有功功率。

2)旋转备用成本函数。

风电出力预测较负荷预测准确性差，因此，系统需提供更多的备用容量来维持其可靠性。而在市场环境下，旋转备用不再由发电商无偿提供，应计入经济调度目标函数中。

为应对大规模风电场出力不确定性对系统造成的影响，引入正、负旋转备用［10］。当风电出力突然下降时，常规机组必须有能力增加发电出力来满足系统功率平衡，即系统所需的正旋转备用容量riu，其成本γi1riu通过风电出力降低时机组出力不够所导致的失负荷价值来衡量;反之，当风电出力突然上升时，常规机组要能降低发电出力使风能得到充分利用，费用γi2rid则通过风电出力上升时，系统预留负旋转备用不够而造成的弃风损失和削减部分发电出力的补偿损失来评估。因此，机组i的旋转备用成本函数表达为

式中 riu，rid分别为机组i的正、负旋转备用容量;γi1，γi2分别为正、负旋转备用成本系数。

3)调度总费用函数。

综上所述，以降低系统调度总费用为目标，考虑发电计划和备用计划联合建模，最小化常规机组发电成本和旋转备用成本，构建目标函数:

式中 N为系统常规发电机组总数;C为所有常规发电机组的调度总费用。

1.2 约束条件

1)功率平衡约束。

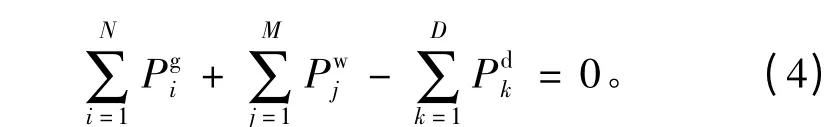
2)发电机组出力约束。

3)系统正、负旋转备用容量约束。

式中 RU，RD分别为系统规定的总的正、负旋转备用容量，一般取系统总负荷的5%左右。

该文侧重点在系统备用容量的获取上，暂不考虑机组爬坡、阀点效应、线路功率越限等因素的影响。

2 条件风险方法的旋转备用调度模型

传统的经济调度模型，约束条件中的正、负旋转备用总量通过确定性方法确定，没有考虑风电场并入后波动性和间歇性的特点，不利于系统安全可靠的运行;同时，对不同风电出力情况下采取固定的备用容量获取方式，并未考虑正、负备用容量的实际充裕水平，从经济角度来讲也不是最优的。因此，需要采用随机性理论方法定量分析由风电不确定性引起的系统旋转备用。

2.1 风险与条件风险

在金融领域风险价值VaR(Value-at-Risk)被广泛应用于风险计量，但存在不满足一致性公理、缺乏次可加性，以及尾部损失测量非充分性等缺陷。因此，为克服其不足，Rockafeller和Uryasev提出条件风险价值CVaR［11］，它是指在一定置信水平上损失超过VaR的条件均值，反映了损失超过VaR阈值时可能遭受的平均潜在损失的大小。CVaR较VaR更能体现潜在风险价值且满足一致性风险度量，具有凸性，适用于任何有风险的优化问题上。

设X为目标组合可行集，X⊂Rn;令f(x，y)为损失函数。其中，x∈X⊂Rn为决策变量，y∈Rm为随机变量;若随机变量y的概率密度函数为ρ(y)，对于确定的x，由y引起的损失f(x，y)是R上服从某一分布的随机变量，其不超过临界值α的分布函数为

对于任意固定的x，ψ(x，α)作为α的函数是在投资组合x下的损失累积分布函数，且它对α非减且右连续。

对于给定的置信度β，VaR和CVaR分别由公式可得［9］，即

由于式(10)fCVaRβ(x)项中含有fVaRβ(x)项，而fVaRβ(x)的解析式难以求出，Rockafeller和Uryasev引入一个函数Fβ(x，α)来计算CVaR:

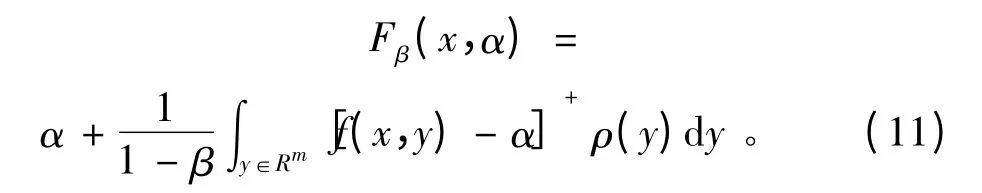
式中［t］+=max {t，0};一般情况下概率密度函数ρ(y)的解析表达式难以得到，可以利用随机变量y的蒙特卡罗模拟样本数据给出式(11)中积分的估计。设y1，y2，…，yM为y的M个样本，则函数Fβ(x，α)的估计值为

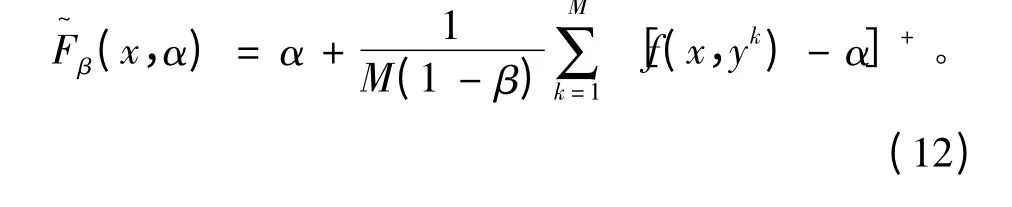
2.2 效益函数的CVaR计算值

条件风险理论中的条件风险值CVaR原本是针对风险的随机性计算方法，风险函数属于成本型函数，即函数值越小越好;而对于系统的旋转备用容量，则属于效益函数，即函数值越大越好。由于效益函数CVaR值的物理意义不再是风险度量，而只是一种随机处理的计算值，为了不与风险概念混淆，称其为效益函数的CVaR值。

2.3 正、负旋转备用函数

电力系统安全调度中，为保证风电并网后的系统功率平衡，引入正、负旋转备用容量。将系统功率平衡等式约束式(4)代入不等式(6)、(7)的左式，以便处理风电随机变量Pwj，因此，可定义正、负旋转备用函数为

2.4 旋转备用的CVaR值

1)满足备用的风电出力概率。

采用CVaR理论对系统正、负旋转备用函数进行刻画，使其在一定置信水平上成立，结合式(8)，应有正、负旋转备用函数u1，u2分别不小于阈值α1，α2的风电出力概率:

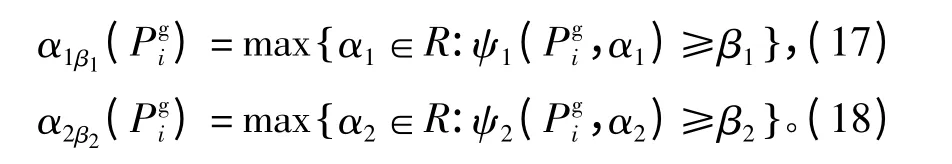
2)旋转备用的CVaR值。

基于以上描述，对照式(9)，由式(10)定义正、负旋转备用的CVaR值:

式(19)、(20)是旋转备用的CVaR值，其代表在风力发电随机因素影响下，满足置信水平β1，β2的系统旋转备用值。

2.5 旋转备用CVaR值的解析表达

1)旋转备用CVaR值的等效函数。

由于式(19)、(20)解析困难，为便于计算，等效计算函数［9，11］为

2)等效函数的离散化。

根据式(11)、(12)的推导，采用蒙特卡罗模拟，通过构造一个功能函数转化为一个凸函数的优化问题，并引入辅助变量zk来化简模型，用离散点去近似代替积分函数，将式(21)、(22)化为

正、负旋转备用的CVaR值反映了系统运行的安全情况，有效考虑了风电、负荷等随机因素对系统安全运行造成的潜在风险，比较符合系统实际运行的要求。

2.6 基于条件风险方法的旋转备用优化模型

模型中目标函数和其他约束条件均不改变，新优化模型中系统旋转备用约束如下。

1)系统正旋转备用容量约束。

2)系统负旋转备用容量约束。

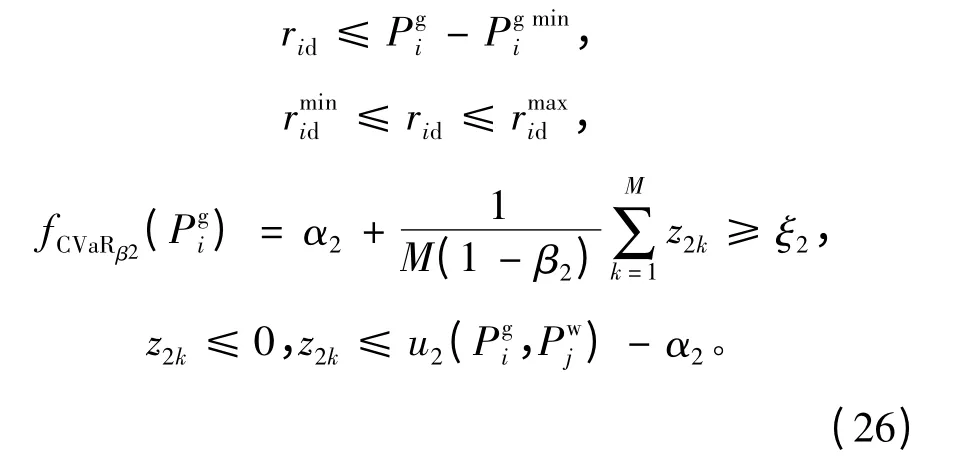
式(25)、(26)中，Pgi，riu，rid为决策变量，风电出力Pwj为随机变量，正、负旋转备用CVaR的取值范围ξ1，ξ2采用线性加权法求取，具体方法可参考文献［12］。

3 算例分析

3.1 算例参数

以文献［13］的IEEE 118节点14机系统为例应用如上方法。第24节点为风电场并网节点，由180台最大出力为2.5 MW的风电机组组成，额定总有功功率为450 MW;系统有功总负荷为2 874 MW;风电功率预测采用Weibull分布，其形状系数k=2.0，尺度系数c=8.5;正、负旋转备用成本系数γi1，γi2均取100$/MW;功率基值为100 MV·A。

3.2 结果分析

1)当风电注入功率为221.33 MW时，在不同置信水平下，系统对应的调度结果如表1所示，可以看出，随着置信水平的提高，正、负旋转备用的CVaR值变大，即对系统运行要求越高，系统所需正、负旋转备用容量越大，此时常规机组调度总费用增加，系统的经济性变差。

2)对比传统的正、负旋转备用模型，即正、负旋转备用总量RU、RD为系统总负荷的5%时的系统发电费用和调度结果如表2所示，表1中条件风险方法的旋转备用模型计算得到的备用容量要大。这是由于考虑了风电出力不确定因素的影响，能更大限度地利用风能资源而减少常规机组出力，因此，不计风能成本的调度总费用比传统确定性模型的要少，符合智能调度的理念。

3)当置信度水平为0.95时，对应不同的风电出力，系统所获取的正、负旋转备用容量和调度费用之间的关系如图1，2所示，可以看出，随着风电出力的增大，常规机组出力降低，因而不计风能成本的系统总调度费用减少。同时，风电出力增加意味着系统不确定性发电量所占比例增大，因此，系统需要更多的正旋转备用来预防这部分随时可能缺失的风电功率;而此时风电出力上升的空间越有限，即风电出力可增加的量越小，其他机组需压低的出力越小，对系统负旋转备用的要求也随之降低。当风电出力降低时，情况相反。

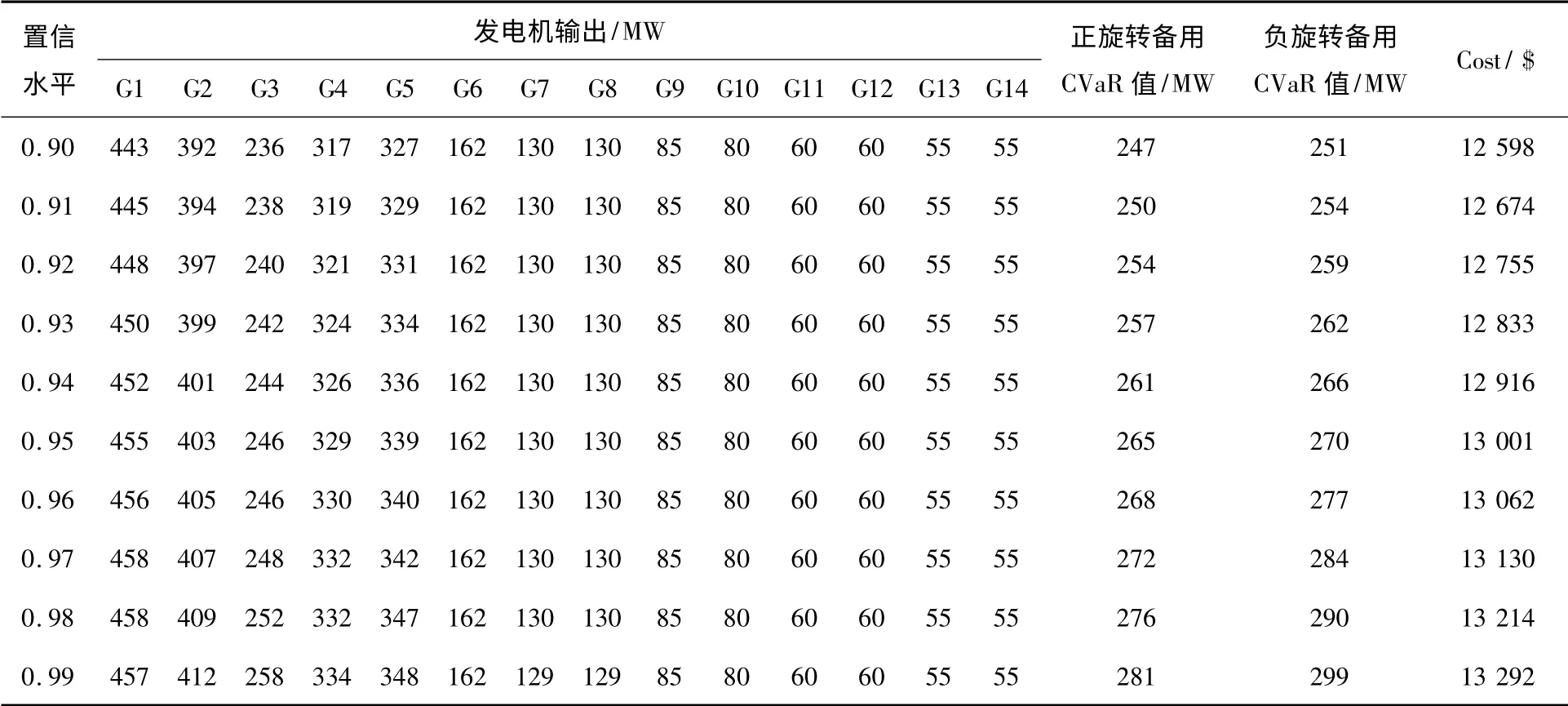
表1 不同置信水平下调度结果及正、负旋转备用CVaR值Table 1 Scheduling results and CVaR value of up and down spinning reserve at different confidence levels

表2 传统模型调度结果Table 2 Traditional scheduling results

图1 调度总费用与风电出力Figure 1 Total cost of scheduling and wind power output

图2 正、负旋转备用CVaR值与风电出力Figure 2 CVaR value of up/down spinning reserve and wind power output

4 结语

条件风险计算方法定量地处理含风电系统旋转备用问题中风电出力随机性带来的影响，可直观地描述旋转备用容量和系统调度费用之间的关系。

目标函数综合考虑了系统发电成本和旋转备用成本;对旋转备用函数取其CVaR值，得到计及随机性和置信水平的旋转备用值，将其计入正、负旋转备用约束中;模型求解采用蒙特卡罗模拟和解析法相结合，快速简捷。

考虑随机因素模型的旋转备用CVaR值比传统确定性计算得到的备用容量要大，因此备用费用增加;但可更大限度地利用风能资源，从而减少常规机组出力，因此调度总费用更低。

不同置信水平对应得到不同的旋转备用CVaR值;置信水平越高，旋转备用值越大;说明旋转备用CVaR值的模型和方法刻画了系统备用容量与经济水平之间的关系。

条件风险方法计算随机性因素，不仅可以解决一般旋转备用问题，也可处理计及潮流约束、机组爬坡约束等因素，并可推广用于电力系统其他随机优化研究。

［1］林勇，陈筱中，郑秀波，等.电力系统旋转事故备用容量的配置研究［J］.电力系统自动化，2014，38(19):114-121.LIN Yong，CHEN Xiao-zhong，ZHENGXiu-bo，et al.Estimation of spinning contingency reserve capacity in power systems［J］.Automation of Electric Power System，2014，38(19):114-121.

［2］赵渊，何媛，芦晶晶.旋转备用对电网可靠性的影响及优化配置研究［J］.电力系统保护与控制，2014，42(8):40-46.ZHAO Yuan，HE Yuan，LU Jing-jing.Allocation optimization of spinning reserve and its effect on bulk power systems reliability［J］.Power System Protection and Control，2014，42(8):40-46.

［3］苏鹏，刘天琪，李兴源.含风电的系统最优旋转备用的确定［J］.电网技术，2010，34(12):158-162.SU Peng，LIU Tian-qi，LI Xing-yuan.Determination of optimal spinning reserve of power grid containing wind［J］.Power System Technology，2010，34(12):158-162.

［4］葛矩，王飞，张粒子.含风电场电力系统旋转备用获取模型［J］.电力系统自动化，2010，34(6):32-35.GE Ju，WANG Fei，ZHANG Li-zi.Spinning reserve model in the wind power integrated power system［J］.Automation of Electric Power System，2010，34(6):32-35.

［5］张放，刘继春，高红均，等.基于风电不确定性的电力系统备用容量获取［J］.电力系统保护与控制，2013，41(13):14-19.ZHANG Fang，LIU Ji-chun，GAO Hong-jun，et al.Reserve capacity model based on the uncertainty of wind power in the power system［J］.Power System Protection and Control，2013，41(13):14-19.

［6］王卿然，谢国辉，张粒子.含风电系统的发用电一体化调度模型［J］.电力系统自动化，2011，35(5):15-18.WANG Qing-ran，XIE Guo-hui，ZHANG Li-zi.An integrated generation consumption dispatch model with wind power［J］.Automation of Electric Power System，2011，35(5):15-18.

［7］杨甲甲，何洋，邹波，等.电力市场环境下燃煤电厂电煤库存优化的CVaR模型［J］.电力系统自动化，2014，38(4):51-59.YANG Jia-jia，HE Yang，ZOU Bo，et al.A CVaR-based coal inventory optimization model for coal-fired power plants in electricity market environment［J］.Automation of Electric Power System，2014，38(4):51-59.

［8］薛志英，周明，李庚银.基于条件风险价值的电力系统短期充裕性决策［J］.中国电机工程学报，2014，34(1):96-104.XUEZhi-ying，ZHOUMing，LIGeng-yin.Short-term adequacy decision of power systems based on CVaR［J］.Proceedings of the CSEE，2014，34(1):96-104.

［9］周任军，刘志勇，闵雄帮，等.不确定性优化方法在电力系统研究中的应用［J］.电力科学与技术学报，2014，29(2):21-29.ZHOU Ren-jun，LIU Zhi-yong，MIN Xiong-bang，et al.A review on application of uncertainty optimization method in power systems［J］.Journal of Electric Power Science and Technology，2014，29(2):21-29.

［10］周玮，孙辉，顾宏，等.计及风险备用约束的含风电场电力系统动态经济调度［J］.中国电机工程学报，2012，32(1):47-55.ZHOU Wei，SUN Hui，GU Hong，et al.Dynamic economic dispatch of wind integrated power systems based on risk reserve constraints［J］.Proceedings of the CSEE，2012，32(1):47-55.

［11］Rockefeller R T，Uryasev S.Conditional value-at-risk forgeneral loss distributions［J］.Journal of Banking and Finance，2002(26):1 443-1 471.

［12］孙欣，吕跃春，高军，等.电网经济性与安全性的精益化协调方法［J］.电网技术，2009，33(11):12-17.SUN Xin，LV Yue-chun，GAO Jun，et al.Power grid economy and security coordination lean method［J］.Power System Technology，2009，33(11):12-17.

［13］Venkatesh P，Gnanadass R，Padhy N P.Comparison and application of evolutionary programming techniques to combined economic emission dispatch with line flow constraints［J］.IEEE Transations on Power Systems，2003，18(2):688-697.