基于代数多项式模型的用电量预测研究

盛立锃，曾喆昭，李 莎

(长沙理工大学 电气与信息工程学院，湖南 长沙 410004)

随着国民经济的快速发展与发展方式的转型、人们生活水平的不断提高，社会用电量均在不断地攀升。由于影响用电量的因素较多且各个因素之间可能相互影响，存在较强的相关性，加上预测的时间长短、精度控制的要求不一，因此，目前对于用电量的预测方法各不相同。

用电量预测的主要思路:通过找出全社会用电量的时序发展规律及其各种相关因素的历史相关性，建立数学模型，通过外推的方法实现预测。目前，常用的单一预测方法一般有插值法［1－2］、灰色预测法［3－4］、回归分析预测法［5－6］、时间序列法［7－10］以及人工智能方法中的人工神经网络［11－12］，这些方法在用电量的预测中均取得了一定的效果。由于单一的预测方法都是基于某一个或几个变化规律的分析，忽略了其他一些因素，因此存在一定的局限性。如何将各种方法合理地组合起来，取长补短，实现优势互补，是解决单一预测法缺陷的一种途径。

组合预测方法的主要思想:选取多个预测模型，按照某个原则(如预测有效度和残差)求取最优组合权系数，将多个模型的预测结果进行拟合。组合预测能有效降低单个模型预测风险，提高预测精度。如贝叶斯理论与支持向量机的结合［13］可以有效地克服数据的不确定性、相关性和非线性的影响;ARIMA模型与神经网络模型的结合［14］可对误差进行修正，改善预测结果;模拟退火算法与神经网络模型结合［15］、粒子群优化算法与神经网络结合［16］可实现神经网络参数优化，改善神经网络的泛化能力。由于组合预测模型在拟合阶段的要求是目标函数值取全局误差平方和最优，因此，所有组合预测都无法避免地要对权重问题进行讨论。用电量受社会、经济、自然条件等众多因素的影响，是一个典型的非线性系统，仅仅依靠有限的因素进行预测显然不足。

为了进一步完善理论体系，笔者提出基于多项式模型与递推最小二乘算法相结合的曲线拟合预测方法，该方法的明显优点在于根据历史数据刻画出模拟函数，找到数据变化的内在变化趋势，实现对模型参数估计。仿真结果表明，笔者提出的方法简单、有效，并且能实现中长期用电量预测。

1 代数多项式神经网络模型

1.1 代数多项式模型

设fd(x)表示x时刻的采样值，f(x)为x时刻的预测值，x∈［a，b］，对x做等效变换:t=(2x－ab)/(b－a)，则－1≤t≤1。

设代数多项式预测模型为

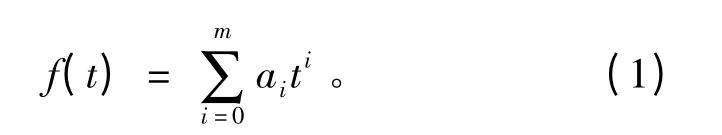
式中 ai(i=0，1，…，m)为加权系数。

为了确定加权系数ai，首先对式(1)离散化，得

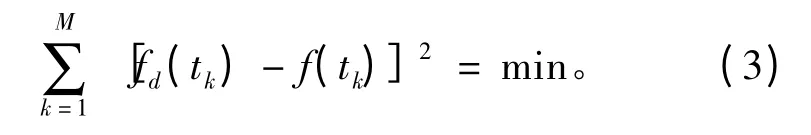
则预测模型是最优的，其中ai为最优预测系数。

设向量:

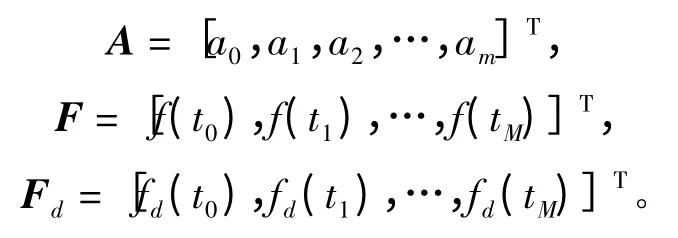
多项式矩阵设为

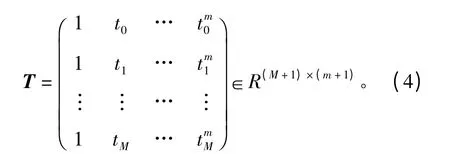
则离散模型式(2)可改写为

或

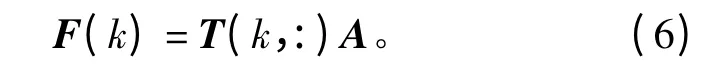
1.2 神经网络模型

根据式(6)可以构建神经网络模型。设输入层至隐含层的权值恒为1，以T(k，j)作为神经网络的隐层神经元激励函数，以A=(a0，a1，…，am)T作为隐层至输出层的权值，神经网络输出为F(k)，神经网络的训练样本集为{k，Fd(k)|k=0，1，…，M}，则神经网络模型如图1所示。

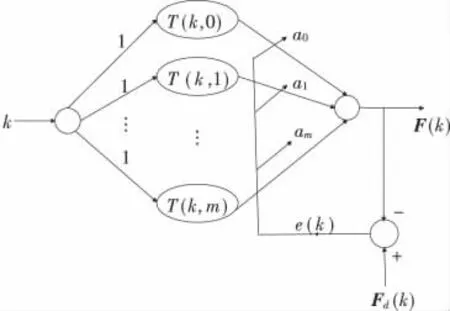
图1 神经网络模型Figure 1 Neural network modal

由图1可知神经网络的输出为

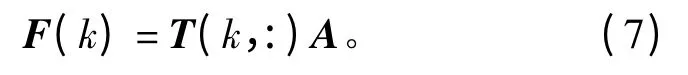
误差函数:

性能指标:

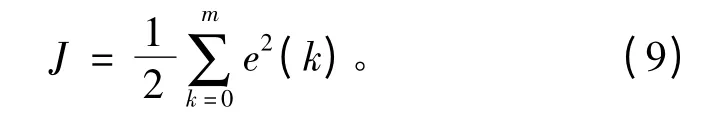
设J=min的权值向量A是一个多变量线性优化问题，因此，根据可得到递推最小二乘法［1，21］:

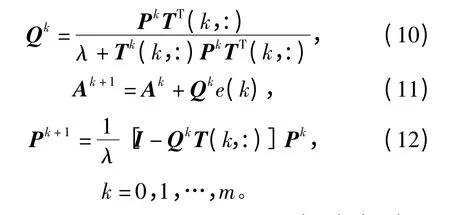
其中，初始协方差矩阵为P0=αI⊂R(m+1)×(m+1)，α是足够大的正数，一般取α=106～109，I∈R(m+1)×(m+1)是单位矩阵;0.90≤λ≤1，若λ=1时，则为基本的递推最小二乘法，通过对样本数据的训练，可获得最优权值向量A。采用迭代方法求解式(5)、(6)，当矩阵T的条件数较大时，收敛速度往往很慢，故T可以采用迭代改善方法求解方程式的收敛速度。

1.3 基于RLS的残差修正方法

假设A*是TA=Fd的准确解，A1是采用RLS方法得到的近似解，则A1的剩余向量［20］为r1=Fd－TA1。

如果y1是Ty=r1的准确解，则A2=A1+y1=A1+T－1r1=A1+T－1(F^d－T^A1)=A1+A*－A1=A*，因此，A2是式(12)的精确解。但是在实际计算的过程中由于舍入误差的影响，A2不会是准确解。于是，再从A2出发计算得A2的剩余向量r2=Fd－T A2，采用RLS方法解方程组Ty=r2，可得y2，再令A3=A2+y2。

重复上述过程可得迭代格式:①计算剩余向量rs=Fd－T As;②采用RLS解方程组Ty=rs得到ys;③更新权值As+1=As+ys;直到满足给定的误差要求结束训练，输出权值向量As+1。

1.4 算法步骤

1)给定多项式的最高次数m，随机产生初始权值向量A=rand(m+1，1);设J=0，0.90≤λ≤1，α=103～106，给定任意小正实数Tol、初始协方差矩阵P0=αI;构造样本向量Fd=［fd(t0)，fd(t1)，…，fd(tM)］T;用式(4)构造多项式矩阵T。

2)k=0，1，…，M，计算神经网络输出F(k)=误差函数e(k)=Fd(k)－F(k)。

4)对权值A采用基于RLS的残差修正方法进行修正;计算误差e1(k)=Fd(k)－TA、性能指标当k≤M+1时，返回步骤2，否则，若J≤Tol，则输出训练权值A，并且计算拟合值F=TA。若都不满足，则返回步骤2重复上述计算。

5)根据预测的时间变量重新构造形如式(4)的多项式矩阵Tp，并利用训练好的权值向量A进行预测计算Fp=TpA。

2 仿真实验

根据中华人民共和国国家统计局提供的2008—2013年各季度的用电量数据对2014—2020年各季度用电总量进行中长期的用电量预测。由于每个季度用电量的变化特性存在差异，故为了便于分析，从4个季度分别进行仿真实验研究，然后将4个季度的用电量合成得到年用电量数据。

在仿真实验中，给定λ=0.90，α=106，每季度多项式曲线拟合的最高次数m分别取值20，25，2，30。仿真结果分别如图2～5所示，每年的实际值与预测值之间的结果对比如图6所示(图中的圆圈表示2008—2013年的采集数据);计算结果分别如表1～5所示。

图2 第1季度用电量拟合与预测结果(m=20)Figure 2 Prediction results of power consumption in the First Quarter(m=20)

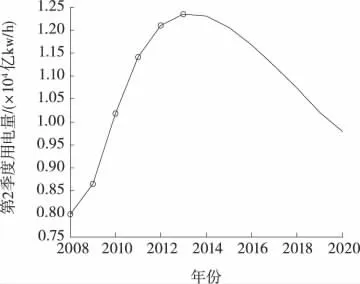
图3 第2季度用电量拟合与预测结果(m=25)Figure 3 Prediction results of power consumption in the Second Quarter(m=25)

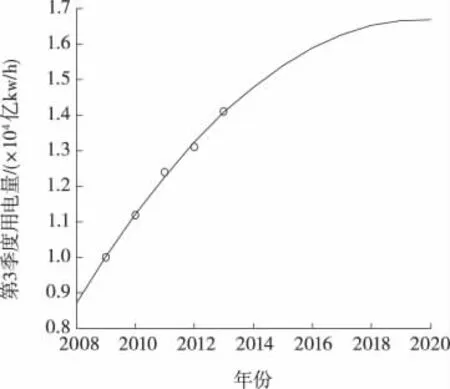
图4 第3季度用电量拟合与预测结果(m=2)Figure 4 Prediction results of power consumption in the Third Quarter(m=2)

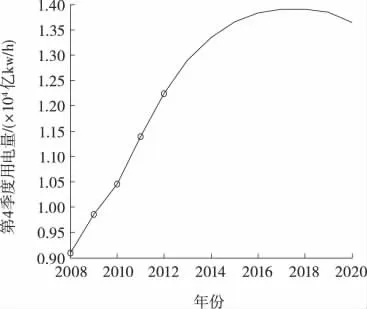
图5 第4季度用电量拟合与预测结果(m=30)Figure 5 Prediction results of power consumption in the Forth Quarter(m=30)

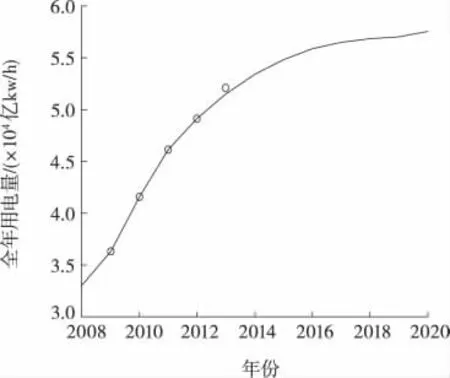
图6 年用电量的实际值与拟合值对比Figure 6 Annual power consumption compare between pratical value and fitting value

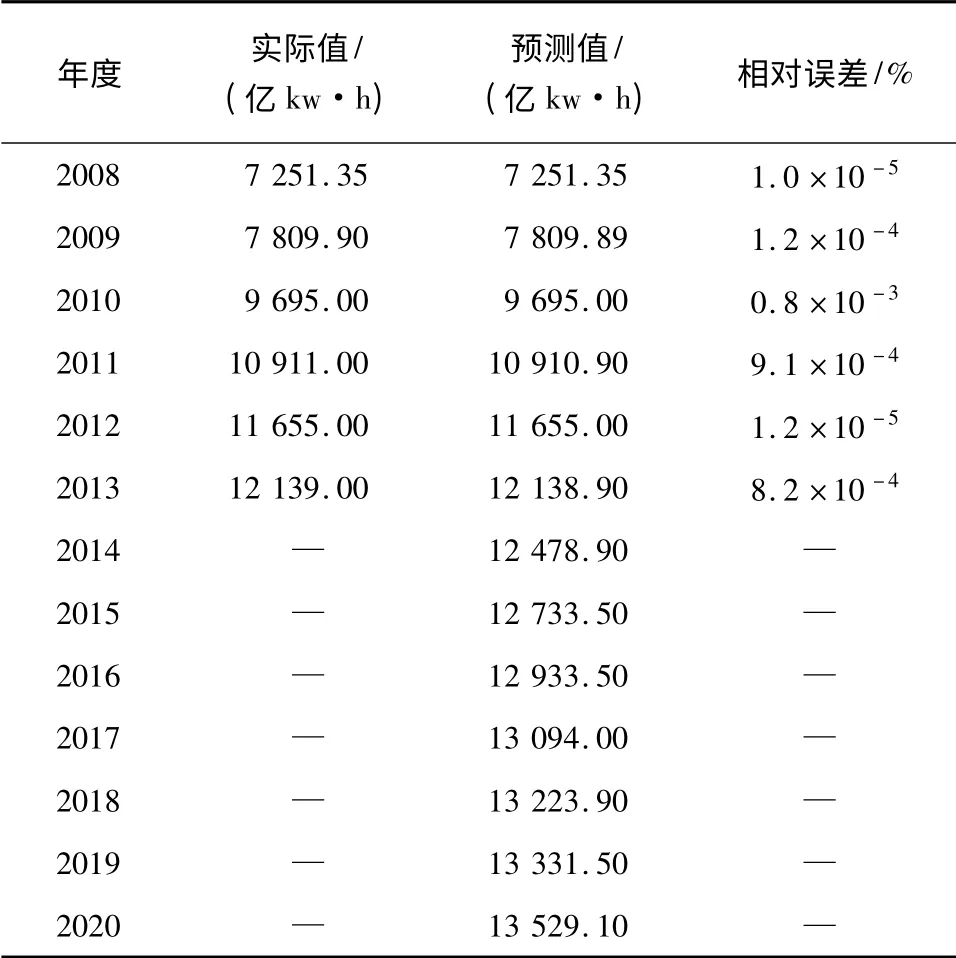
表1 2008—2020年第1季度用电量拟合与预测结果Table 1 Power consumption fitting and prediction results in the first quarter from 2008 to 2020

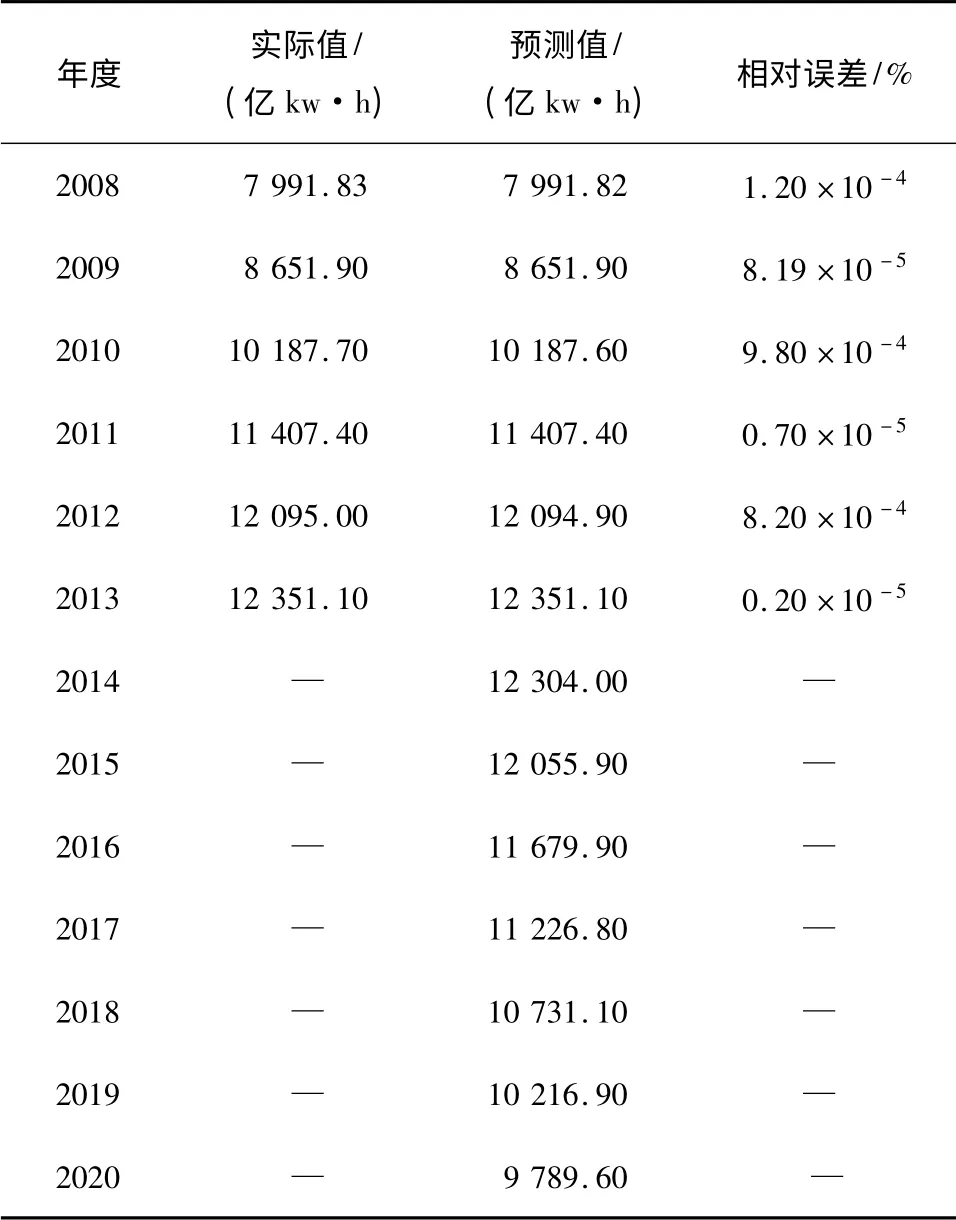
表2 2008－2020年第2季度用电量拟合与预测结果Table 2 Power consumption fitting and prediction results in the second quarter from 2008 to 2020

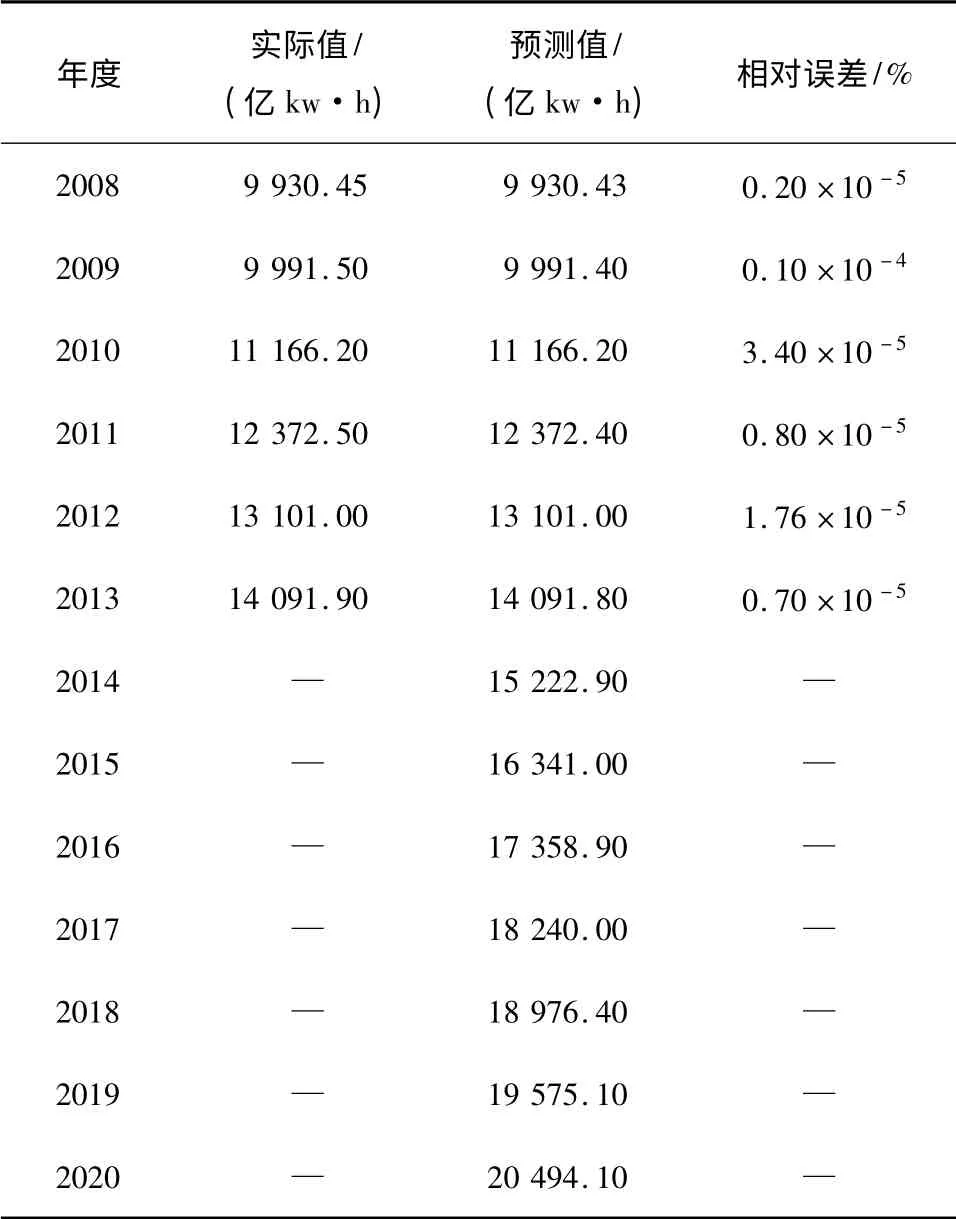
表3 2008－2020年第3季度用电量拟合与预测结果Table 3 Power consumption fitting and prediction results in the third quarter from 2008 to 2020

表4 2008－2020年第4季度用电量拟合与预测结果Table 4 Power consumption fitting and prediction results in the forth quarter from 2008 to 2020

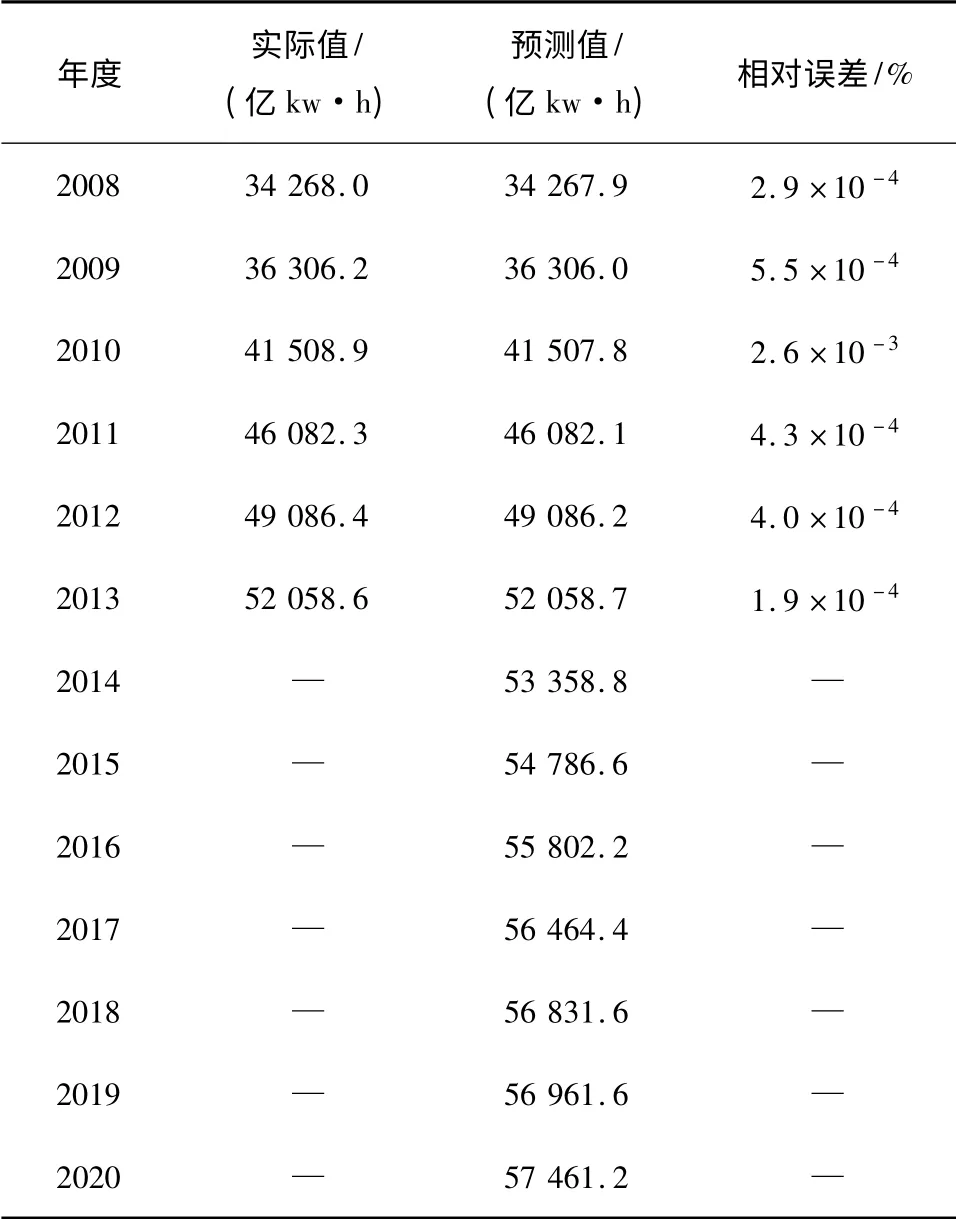
表5 2008－2020年年度用电量拟合与预测结果Table 5 Power consumption fitting and prediction results from 2008 to 2020

图6是根据图2～5合成得到的年用电量变化曲线，由图可知，2014年后年用电量呈缓慢上升的趋势，符合实际情况。由表5可知，年用电量的拟合精度可以达到2.6×10－3%以上，计算结果与文献［8］的预测结果相比，预测精度提高了3个数量级。此外，从文献［8］对2012和2013年度的预测结果来看，与实际情况相差很大。笔者认为，文献［8］尽管在现有研究基础上做了大量的改进工作，并取得了明显研究结果，但是仍然存在较大的模型误差。

3 结语

研究结果表明，笔者提出的基于代数多项式神经网络预测方法不仅拟合精度高，而且能有效实现中长期的用电量预测，因而是一种有效的预测方法，可为决策部门提供有效的用电量预测依据。

［1］曾喆昭，黄创霞，周富照.数值计算方法与应用(第1版)［M］.北京:科学出版社，2013.

［2］王晓佳，沈建新，杨善林.基于Gauss插值的正交化预测方法在智能电网用电量预测中的应用研究［J］.电力系统保护与控制，2010，38(21):141-145，151.WANG Xiao-jia，SHEN Jian-xin，YANG Shan-lin.Application research on Gaussian orthogonal interpolation method for electricity consumption of smart grid［J］.Power System Protection and Control，2010，38(21):141-145，151.

［3］李咏凯，张建华，王国栋，等.一种新的灰色模型在城市年用电量预测中的应用［J］.现代电力，2010，27(4):13-16.LI Yong-kai，ZHANG Jian-hua，WANG Guo-dong，et al.Application of a new grey model to city electricity demand forecasting［J］.Modern Power，2010，27(4):13-16.

［4］周德强.基于最小一乘法的GM(1.1)模型及在负荷预测中的应用［J］.电力系统保护与控制，2011，39(1):100-103.ZHOU De-qiang.GM(1.1)model based on least absolute deviation and its application in the power load forecasting［J］.Power System Protection and Control，2011，39(1):100-103.

［5］曾鸣，李定林，孙晓菲，等.贵州省2015—2020年用电量预测及其比较［J］.水电能源科学，2013，31(4):229-232.ZENG Ming，LI Ding-lin，SUN Xiao-fei，et al.Forecasting the requirements of electricity in guizhou province in 2015—2020 and its comparison［J］.Water Resources and Power，2013，31(4):229-232.

［6］仇芝，党耀国.用电量的灰色—多元回归耦合模型预测［J］.华东电力，2006，34(3):4-7.QIU Zhi，DANG Yao-guo.Electricity consumption forecasting by coupled models of gray forecast and multiple regression［J］.East China Electric Power，2006，34(3):4-7.

［7］雷绍兰，孙才新，周湶，等.电力短期负荷的多变量时间序列线性回归预测方法研究［J］.中国电机工程学报，2006，26(2):25-29.LEI Shao-lan，SUN Cai-xin，ZHOU Quan，et al.The research of line modle of short-term electrical load on multivariate time series［J］.Proceedings of the CSEE，2006，26(2):25-29.

［8］范德成，王韶华，张伟.季度周期模型在我国用电量预测中的应用研究［J］.电网技术，2012，36(7):106-110.FAN De-cheng，WANG Shao-hua，ZHANG Wei.Study on application of seasonal cycle model in China’s power load forecasting［J］.Power System Technology，2012，36(7):106-110.

［9］刘晓娟，方建安.综合权重的模糊时间序列的电力负荷预测方法［J］华东电力，2012，40(4):518-540.LIU Xiao-juan，FANG Jian-an.Weighted fuzzy time-series method for power load forecasting［J］.East China Electric Power，2012，40(4):518-540.

［10］刘辉，田红旗，李燕飞.基于小波分析法与滚动式时间序列法的风电场风速短期预测优化算法［J］.中南大学学报:自然科学版，2010，41(1):370-375.LIU Hui，TIAN Hong-qi，LI Yan-fei.Short-term forecast optimization algorithm forwind speed from wind farms based on wavelet analysis methodand rolling time series method［J］.Journal of Central South University:Science and Technology，2010，41(1):370-375.

［11］陈国初.文化微粒群神经网络在用电量预测中的应用［J］.电力系统及其自动化学报，2011，23(2):31-37.CHEN Guo-chu.Application of cultural particle swarm optimization neural network in electricity load forecast［J］.Proceedings of the CSU-EPSA，2011，23(2):31-37.

［12］崔亚，任明炜.基于多重分类器模型的微网短期负荷预测［J］.电力科学与技术学报，2014，29(1):55-58.CUI Ya，REN Ming-wei.The application of multiple classifier system in microgrid＇s short term load forecasting［J］.Journal of Electric power Science and Technology，2014，29(1):55-58.

［13］呼文亮，王惠文.基于贝叶斯准则的支持向量机预测模型［J］.北京航空航天大学学报，2010，36(4):486-489.HU Wen-liang，WANG Hui-wen.Prediction modeling based on Bayes support vector machine［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36(4):486-489.

［14］刘全，刘汀.基于ARIMA的多元时间序列神经网络预测模型研究［J］.统计与决策，2009(11):23-25.LIU Quan，LIU Ting.Multivariate time series neural network prediction model based on ARIMA［J］.Theoretical Research，2009，11:23-25.

［15］杨天鹏，马齐爽，谢清明.基于神经网络的电磁干扰的预测［J］.北京航空航天大学学报，2013，39(5):698-705.YANG Tian-peng，MA Qi-shuang，XIE Qing-ming.Prediction of electromagnetic interference based on neural network［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39(5):698-705.

［16］陆宁，周建中，何耀耀.粒子群优化的神经网络模型在短期负荷预测中的应用［J］.电力系统保护与控制，2010，38(12):65-68.LU Ning，ZHOU Jian-zhong，HE Yao-yao.Particle swarm optimization-based neural network model for short-term load forecasting［J］.Power System Protection and Control，2010，38(12):65-68.

［17］赵军辉，吕宸.基于多项式拟合的OFDM系统符号盲同步算法［J］.系统工程与电子技术，2013，35(3):619-623.ZHAO Jun-hui，LV Chen.Blind symbol synchronization arithmetic for OFDM system based on polynomial fitting［J］.Systems Engineering and Electronics，2013，35(3):619-623.

［18］刘慧婷，张旻，程家兴.基于多项式拟合算法的EMD端点问题的处理［J］.计算机工程与应用，2004(16):84-86，100.LIU Hui-ting，ZHANG Min，CHENG Jia-xing.Dealing with the end issue of EMD based on polynomial fitting algorithm［J］.Computer Engineering and Applications，2004(16):84-86.

［19］赵静，尹慧芳，党亚民，等.基于多项式拟合的移去恢复法求解对流层天顶延迟的研究［J］.测绘科学，2013，38(4):52-54.ZHAO Jing，YIN Hui-fang，DANG Ya-min，et al.A solution of zenith tropospheric delay based on polynomial fitting［J］.Science of Surveying and Mapping，2013，38(4):52-54.

［20］曾喆昭，文卉.数值计算(第1版)［M］.北京:清华大学出版社，2005.

［21］曾喆昭.神经计算原理及其应用技术(第1版)［M］.北京:科学出版社，2012.