结合RANSAC的SIFT算法在交通视频检测中的稳像技术研究

吴承隆

（1.同济大学 电子与信息工程学院，上海 201804；2.宁波市杭州湾大桥发展有限公司 浙江 宁波 315327）

利用视频事件检测设备对公路突发事件进行检测的应用目前已极为普遍，多数高速公路的隧道、桥梁、岔路口等区域均基本安装了视频交通事件检测器，其有着24小时不间断实时检测的优势，对及时发现交通异常事件、降低事故发生有着重要作用。此外，其作为智能交通领域发展的一项重要内容，近年来也始终被作为领域内研究的热点[1]。

但由于视频检测设备需依靠监控视频作为分析基础，因此视频源的稳定与成像质量是保证检测准确率的重要条件，对于一些气候环境较为恶劣的区域，如跨海长桥、山区、沿海公路等，大风、雨、雾天气众多，由于摄像机安装位置普遍较高，受风后易抖动，从而造成采集的视频图像不稳定，给视频分析造成干扰，因此，需对视频作进一步的稳像处理，以便得到稳定的视频来提高目标匹配的准确性。

电子稳像技术是一种新型的图像稳定技术，与传统的机械和光学稳像系统相比具有易操作、稳像精度高、灵活性强、高智能化等优点，且在图像拼接、图像增强、信息融合、目标识别、目标更正方面能较好地得以运用。目前，视频图像稳定的方法众多，在特制提取匹配中有块匹配法、光流法、角点检测法、像素递归法等[2-4]。

现有交通事件的智能检测普遍是基于监控视频，但对于一些气候环境较为恶劣的区域，如大风、雨、雾天气，给视频的动态检测带来了困难，尤其是在大风天气，摄像机自身的抖动导致图像的不稳定，且对视频分析造成干扰的特征明显。

针对大风恶劣环境下，摄像机存在抖动、偏移使图像序列存在复杂抖动噪声的问题，本文提出了一种结合RANSAC[5]和SIFT[6]算法的视频稳像技术：首先用SIFT算法找到相邻两帧的匹配点，然后用RANSAC算法去除一些无效点，并最终利用最小二乘法估计两帧之间的旋转角θ和位移Δx、Δy。

1 SIFT算法

1999年David G.LoweSIFT在总结基于不变量技术的特征提取方法上，提出了一种对图像旋转、缩放或仿射变换保持不变性的、基于尺度空间的图像局部描述特征算子，并在2004年对其进行了进一步的发展与完善。SIFT算子具有旋转、平移、尺度的不变性，且对仿射变换、3维投影变换和光照变化具有一定的鲁棒性。Mikolajczyk对10种包括SIFT算子在内的局部描述特征做了不变性对比实验，证实SIFT与其扩展算法在同类描述特征中具有最强鲁棒性。

其的特下如点：1）唯一性。SIFT算法对于每个特征点均有相应的特征描述子，适于在大量特征数据库中准确、快速地进行匹配。2）多量性。即使少数几个物体也可产生大量SIFT特征向量组，完全可反映出图像中的信息。3）适应性。对于缩放、旋转及光照等情景的视频，SIFT算法具有良好的适应性，且经过优化可满足一定的实时性要求。4）可扩展性。能方便地与其他类型的特征点和特征向量相结合，具有良好的相容性。SIFT应用范围广泛，其中包括目标识别、机器人视觉、图像检索、3D建模、图像拼接、动态匹配、视频跟踪和手势识别。

SIFT算法实现步骤实现如下：

1）检测得到极值点尺度空间。

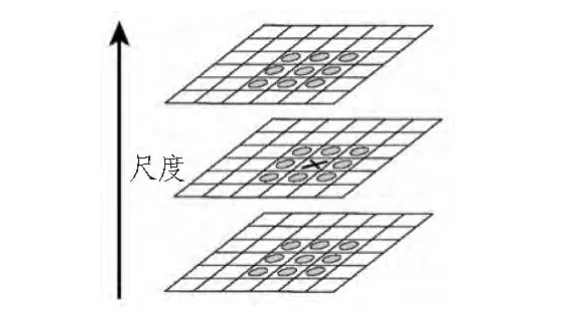
图1 DoG尺度空间局部极值点检测Fig.1 DoG scale space local extreme point detection

图1 所示3个相邻的DoG空间尺度。在尺度空间极值检测时，标记点有必要和穿过周围同等规模附近的89×2像素与相邻像素周围的刻度对应位置的邻域在整个26个像素相比较，以确保在尺度空间和二维图像空间中均可检测到局部最小值。

2）通过拟合的二次函数来准确判定关键点的三维位置及尺度，同时除去关键点与不稳定点的低对比度边缘 （因DoG算子会产生强烈的边缘响应）响应，以增强匹配的稳定性，从而提高抗噪声能力。

3）梯度方向使用关键点的邻近像素分布特征为在指定方向参数，每一关键点，使算子有旋转不变性

式（1）为（x，y）的梯度方向和模量。 其中，L 的尺度是用于每个关键点所在的尺度。在实际计算中，利用以关键点为中心的窗口采样，邻近像素的梯度方向用直方图统计。0°～360°为梯度直方图的范围。其中，每列隔10°，总共36列。直方图的峰代表关键点的梯度主方向，其可作为关键点的方向。图2为利用梯度确定主方向的示例。

图2 由梯度方向直方图的主梯度方向确定Fig.2 Main gradient direction is determined by the gradient direction histogram

梯度方向直方图中，当存在另外80%对应于该峰的主峰能量时，则该方向是辅助关键点的方向。一键可与多个方向（一个主方向，一个以上的辅助方向），增强匹配的鲁棒性来指定。在这一点上，图像的关键点已完成检测，每个关键点有3条信息：位置、方向和尺度。其可决定一个SIFT的特征区域。

4）SIFT特征向量生成。首先，对关键点的方向旋转轴线，以确保旋转的不变性。

图3 由关键点邻域梯度信息生成特征向量Fig.3 Feature vectors generated by the critical point neighborhood gradient information

在该窗口中心的下一个关键点取8×8中部的黑点，在图3中为当前关键点的左侧部分，代表各小邻域内的关键点像素网格的位置。其中尺度空间中，箭头表示其像素值的梯度方向渐变模式的长度，蓝色图形高斯彩色圆圈代表加权范围（像素梯度方向接近的信息贡献的关键点更大）。随后直方图计算8个方向中绘制每个梯度的累积值方向上每4×4块的梯度方向，并可将种子点右侧部，如图3中的一个关键点来形成图中的4个2×2种子之和，每个种子点的矢量信息有8个方向。邻域的共同方向信息的概念提高了抗噪算法的能力，其包括定位误差匹配功能，且还提供了一个更好的容错能力。

在实际的计算过程中，为了增强匹配的鲁棒性，Lowe建议使用4×4得16的每个关键点来描述种子点。因此，对于一个关键点数据，可产生128个数据，该最终维的SIFT特征向量。此时，SIFT特征向量已被移除几何畸变因子尺度变化，旋转效果，然后继续该特征矢量归一化的长度，则可进一步去除光照变化所带来的影响。

当两个图像SIFT特征向量生成，文中使用欧几里德距离的关键特征矢量下一个步骤，以确定两个图像测量一个关键点的相似性。关键点取一个的图像，并发现这两个关键点的欧几里德距离与图像中的两个最近的前两个关键点中，若最近的距离除以小于该比率阈值，则由时间接近的距离验收这对匹配点。由此，降低了该阈值比率，虽SIFT匹配点的数量减少，但却更加稳定。

2 RANSAC算法

基本假设RANSAC算法是将样品中包含正确的数据（inliers可由数据模型来描述）和异常数据（Outliers从正常范围偏离较远，无法适应数据的数学模型），该数据集包含的噪声。这些异常可能是由于错误的数据测量和错误的假设在误差的计算中产生。同时，RANSAC还假定，给定一组正确的数据，有一种方法来计算模型参数与这些数据相一致。

RANSAC基本思想如下所述：1）虑n最小可能的模型样本组 （n为初始化模型参数所需的最小采样数）和P的样本集，样本的数量设定在P＃（P）＞N，在P中所含的随机NP样本初始化模式子集SM；2）在错误的模型M设定SC=P/S小于一组阈值t与样本集S构成S*。S*认为是点的集合，其构成了一个集合 S（Consensus Set）一致；3）如 ＃（S*）≥N，认为要得到正确的模型参数，并利用集合S*（内点inliers）采用最小二乘法重新计算新模型M*，再随机选择新的S，重复上述过程。由此确定最大一致性组的内部和外部点；4）完成一定数目的样本后，若该算法找到一致集失败，反之被抽选时，算法结束。

综上所述，有两种可能的算法优化策略。 1）若可尝试到一些具体方案的选择使用已知的特性或具有约束选择的S随机选择的子集，以取代完全随机选择的原件；2）当一致集为S*M*计算模型后，可成为模型误差的所有PM*小于样本 t加入S*，再重新计算 M*。

RANSAC算法包括3个输入参数：1）确定样品是否满足误差容忍度t。t可被看作是噪声方差的一个内部点被假定为不同的输入数据，需通过预先设定阈值的方式进行人工干预，且参数对RANSAC性能有较大影响；2）随机选取的样本集合S倍。该参数直接影响所涉及的SC模型参数，进而也会影响该算法的效率；3）鉴定，一致集大小S*N。为了保证获得数据集P模式的正确表征，与设置足够大的总体要求相一致。此外，样本一致较多，使重新估计模型参数更为精确。RANSAC算法通常用于在计算机视觉。例如，在立体视觉摄像机的视场，同时解决的匹配点问题的计算和基本矩阵。

3 最小二乘法

3.1 线性模型

在等权、独立、无系统误差的n个测量条件下，通常可写成如下线性模型

式中 l（n×1）是决定于直接测量值的已知向量，A（n×t）是决定于测量方案和程序的已知设计矩阵，测量值l1，…，ln的方差σ2和参数x（t×1）待求，若在最小方差意义下求得的x估计值为x^，则 E（l）=Ax，也可写为 v=l－Ax^。 此处，v（n×1）为残差向量，求解时约定 n≥t，rkA=t。

3.2 最小方差意义下线性无偏估计及其协差阵

由前知方差与残差平方和成正比，欲使解得的量具有最小方差，则可使v′v=min，即最小二乘法，现令

注意到式（2）、（3）则有

所以

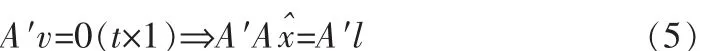
上式通常称为法方程或正规方程，因 rk（A′A）=t，故 A′A的逆存在，可得到唯一解

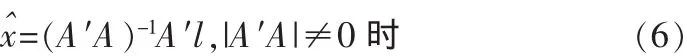
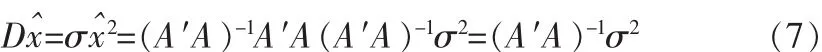
3.3 伪逆矩阵

1）右伪逆矩阵。定义 1设A是m×n阶矩阵，规定ARM=A′（AA′）－1叫右伪逆矩阵。由此，定义的右伪逆矩阵确实具有逆矩阵的性质

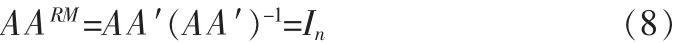
2）左伪逆矩阵。定义2设A是m×n阶矩阵 ，规定ALM=（AA′）－1A′叫左伪逆矩阵。由此，定义的左伪逆矩阵确实具有逆矩阵的性质

则式（6）可写为

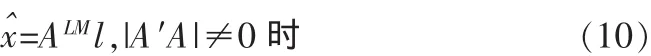
4 稳像技术步骤及实验结果

1）利用SIFT算法计算前后两帧的关键点，并找出两帧之间的匹配点对；

2）采用RANSAC算法去除无效的匹配点对；

3）利用最小二乘法估算两帧之间的旋转角θ和位移Δx、Δy参数。

4）根据计算得到的旋转角和位移参数[7]旋转并平移后一帧。

实验将相邻的三帧合成RGB图，其结果如图4、图5所示。

图4 稳像前的三帧RGB合成图Fig.4 Three frames RGB composite image stabilization before

图5 稳像后的三帧RGB合成图Fig.5 Three frames RGB composite image after image stabilization

由上图可知，稳像前的图片较为模糊且有重影，因相机存在抖动，而稳像后的图片则较清晰。

5 结束语

本文提出了一种结合RANSAC和SIFT算法的视频稳像技术，并将其应用于实际的项目中。实践结果表明，在大风恶劣的实际情况下，导致摄像机抖动、偏移，并使图像序列存在复杂抖动噪声等问题，均可通过该方法得到了有效解决。

[1]赵菲.视频稳像技术研究[D].长沙:国防科学技术大学，2007.

[2]张国栋.基于电子稳像技术的视频稳像技术研究 [D].太原:中北大学，2010.

[3]张翠，吴诚，郑晟，等.基于TMS320C642电子稳像算法的实现[J].电子科技，2011，24（4）:57-58.ZHANG Cui，WU Cheng，ZHENG Sheng，et al.Based on TMS320C642 electronic image stabilization algorithm implementation[J].Electronic Technology，2011，24（4）:57-58.

[4]刘玉红，涂丹.数字图像稳像算法研究 [J].计算机仿真，2008，25（27）:200-204.LIU Yu-hong，TU Dan.Digital image stabilization algorithm research as[J].Computer Simulation，2008，25（27）:200-204.

[5]曾雪莲.一种新的快速智能电子稳像算法[J].兵工学报，2008，29（11）:1384-1388.ZENG Xue-lian.A new fast algorithm for intelligent electronic imagestabilization[J].Ordnance，2008，29 （11）:1384-1388.

[6]刘明，赵跃进，周渝斌.电子稳像中的运动补偿矢量处理方法的研究[J].光学技术，2005，31（3）:457-462.LIU Ming，ZHAO Yue-jin，ZHOU Yu-bin.Research on electronic image stabilization motion compensation vector processing method[J].Optical Technology，2005，31（3）:457-462.

[7]何志勇，宋少伟，邓长华，等.瞬态时域数据合成冲击响应谱算法研究[J].火箭推进，2013（5）：55-59.HE Zhi-yong，SONG Shao-wei，DENG Chang-hua，et al.Research on transient time-domain data synthesis of shock response spectrum[J].Journal of Rocket Propulsion，2013（5）：55-59.