大锥度线切割加工电极丝中心轨迹的一种线性化方法

冯锡平，谭 民，郭 岗

（1.中国科学院自动化研究所复杂系统管理与控制国家重点实验室，北京100190；2.北京南讯威达科技有限公司，北京100096）

大锥度线切割机床是加工成形刀具、塑料模、拉丝模、挤出模的主要设备之一，随着工件形状的不断变化和大锥度机床机械结构的改进，上下异形的复杂直纹面加工越来越普遍。在“无锥度”的直升面加工时，电极丝与工件端面始终垂直，电极丝的中心轨迹可通过等距离偏移工件轮廓来生成。当加工锥度工件时，电极丝将倾斜，其在工件上、下表面的横截面将从“圆形”变为“椭圆形”；当电极丝倾斜角度＞15°时，“椭圆度误差”成为影响加工精度的主要因素之一[1]。因此，在大锥度加工时，如何精确求取电极丝的中心轨迹是提高加工精度的关键所在。为此，研究人员提出了“椭圆偏置法”[2-3]和“广义电极丝模型”方法[4]。更进一步，在大锥度异形加工时，用上述两种方法求取的“工件上、下表面电极丝中心轨迹曲线”为非规则曲线，无法用文献[5]所提的方法进行线性化。因此，必须找到一种线性化方法，将“工件上、下表面电极丝中心轨迹的非规则曲线”同步线性化为多组“小直线对”，以满足大锥度线切割加工的要求。

本文首先介绍了如何使用 “广义电极丝模型”方法来求取电极丝的中心轨迹，在此基础上，提出了用“二次高分辨率采样方法”同步线性化非规则的上、下表面电极丝中心轨迹曲线，并给出了算法的实现过程，最后通过仿真验证了算法的正确性。

1 电极丝中心轨迹求取分析

混合直纹面基本理论是“广义电极丝模型”（图1）[4]方法的基础，混合直纹面上任意一点S的坐标可表示为：

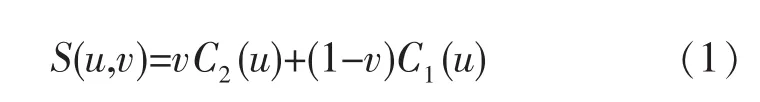
式中：u 为路程参数；v∈[0,1]。

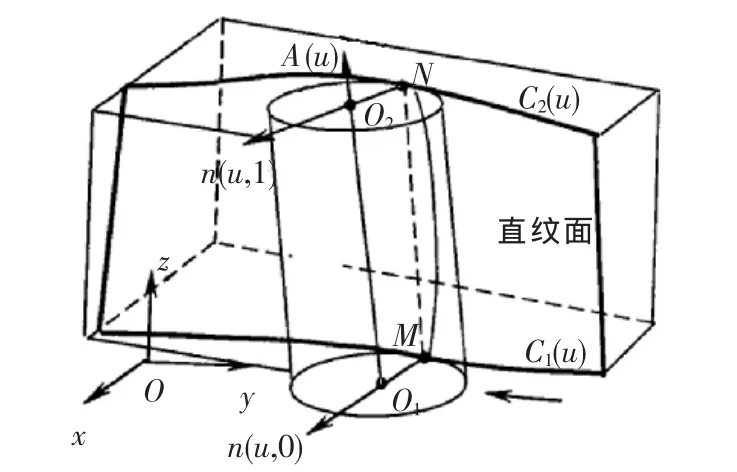
图1 广义电极丝模型

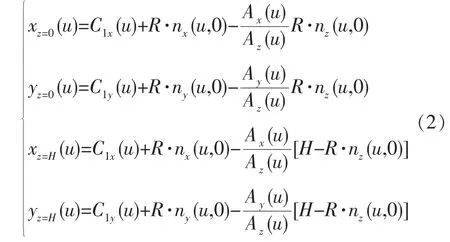
式中：C1x(u)和C1y(u)为工件下表面曲线的x和y坐标，可根据路程参数u的值求出；R为广义电极丝半径的值，是加工所用的“电极丝半径”、“放电间隙”及“单边余量”3 个值的总和；nx(u,0)、ny(u,0)和 nz(u,0)分别为直纹面S导线C1(u)上的法向矢量n(u,0)在x、y和z轴的分量，可由式（3）计算得出：

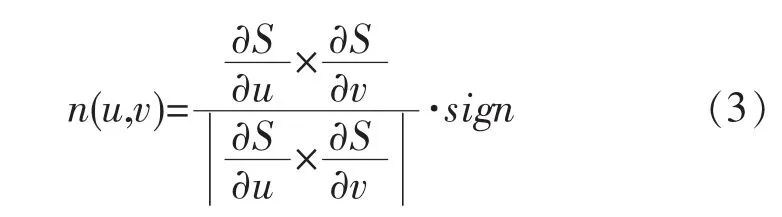
式中：sign为符号函数，根据轨迹方向和补偿方向的不同，取值为+1或-1。

由式（3）可知，当导线 C1(u)和 C2(u)已知时，n(u,0)为路径参数 u的函数，可知 nx(u,0)、ny(u,0)和 nz(u,0)也为路径参数 u 的函数。式（2）中的 Ax(u)、Ay(u)和Az(u)为图1所示电极丝轴线O1O2的方向矢量A(u)在X、Y和Z轴的分量，由式（4）计算得出：

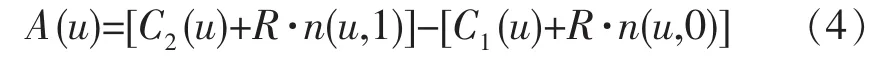
由式（4）可知，当导线 C1(u)、C2(u)和 R 已知时，Ax(u)、Ay(u)和Az(u)也是路程参数u的函数。

通过上述说明和讨论可知，当导线C1(u)和C2(u)方程已知，且R和H值已知时，可通过代入路程参数u求出工件上、下表面的电极丝中心轨迹坐标。本文用MATLAB实现文献[4]给出的“广义电极丝模型”方法，并给出用该方法求取“大锥度加工电极丝中心轨迹”的几个仿真实例。

仿真1：上、下表面均为直线；直线方程分别为上表面 y1=x1，x1∈[-5，8]，下表面 y2=-x2，x2∈[-5，8]；工件厚度H=20 mm；广义电极丝半径R=0.2 mm；外补偿。仿真结果见图2。

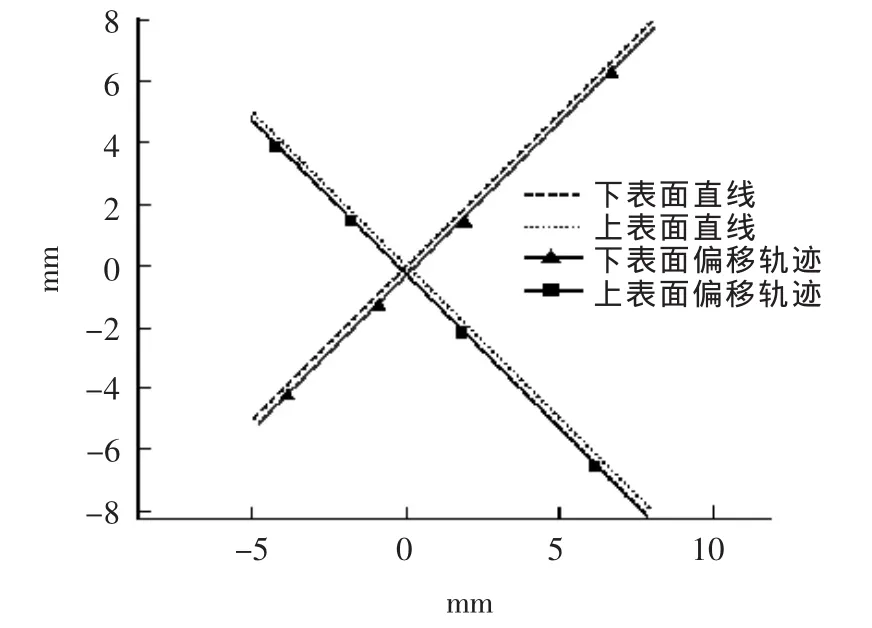
图2 上下表面均为直线及其偏移后的电极丝中心轨迹

在无锥度和小锥度加工轨迹编程时，如果已知“待加工工件”的轨迹（原始轨迹）和广义电极丝半径R值，可对“待加工工件”的轨迹做等距离偏移生成新的轨迹（偏移轨迹）。原始轨迹和偏移轨迹的偏移距离为定值，即广义电极丝半径R的值。在仿真1中，通过仿真给出“广义电极丝模型”方法生成大锥度加工电极丝中心轨迹与原始轨迹之间的距离差值，并在此基础上减去广义电极丝半径R的值，结果见图3。

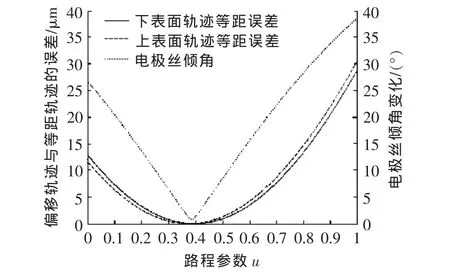
图3 上下均为直线的电极丝倾角变化及等距误差

从图3可看出，仿真1给出的偏移后的电极丝中心轨迹非直线，如果此时对原始轨迹做等距离偏移，那么，偏移后的轨迹与大锥度实际加工时电极丝的理论中心轨迹之间将产生最大30 μm的切割误差。因此，必须找到一种线性化方法，将用广义电极丝模型方法求取出的大锥度线切割加工的上下表面电极丝中心轨迹线性化为小直线，将由于大锥度加工时电极丝倾斜导致的横截面变为椭圆带来的编程误差控制在允许的范围内。

仿真2：下表面加工轨迹为直线，直线的起始坐标为[-10.607，0]，终点坐标为[0，-10.607]；上表面加工代码为圆弧，其圆心坐标为[0，0]，起始角和终止角为[π，1.5π]，半径为 15 mm；工件厚度 H=10 mm；广义电极丝半径R=0.18 mm；外补偿。仿真结果见图4和图5。

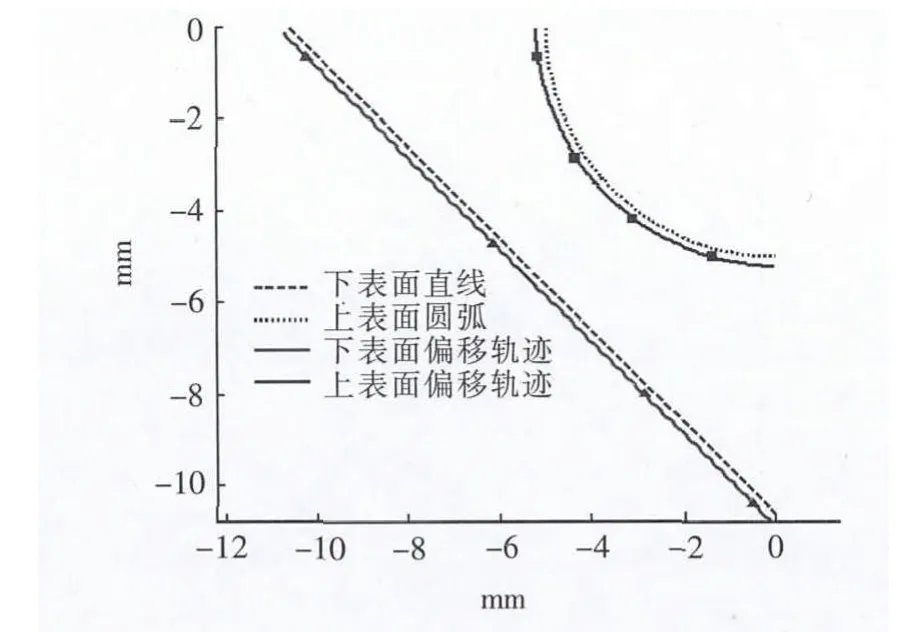
图4 上表面圆弧、下表面直线的中心轨迹图

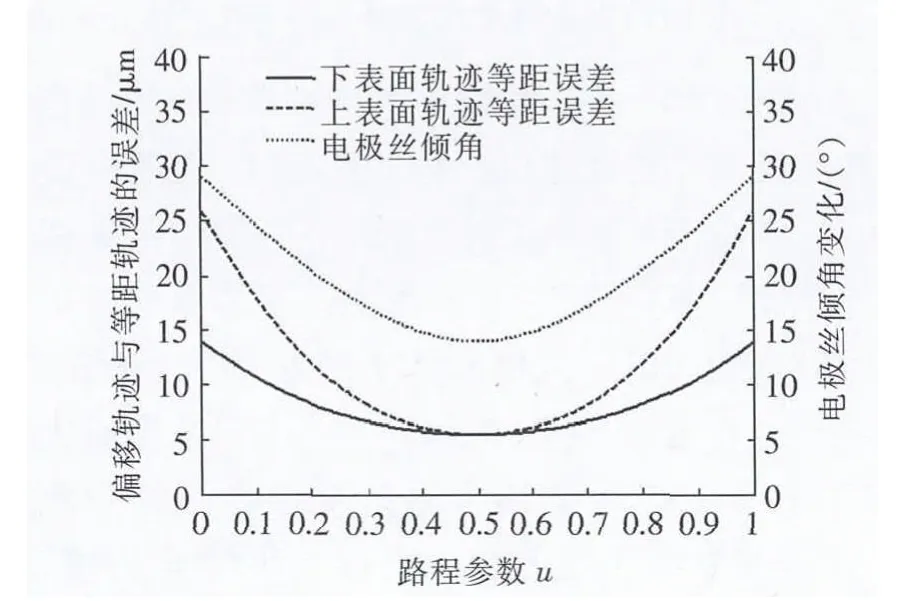
图5 上表面圆弧、下表面直线的电极丝倾角及误差

从图4和图5可看出，下表面为直线、上表面为圆弧的大锥度加工，其上、下表面电极丝的中心轨迹都发生了“畸变”，而非简单的圆和直线。如果采用传统方法做等距离偏移并加工，将导致下表面产生最大14 μm的加工误差，上表面产生最大25 μm的加工误差。

仿真3：下表面加工代码为圆弧，其圆心坐标为[0，0]，起始角和终止角为[π，1.5π]，半径为 15 mm；上表面加工代码为圆弧，其圆心坐标为[1，2]，起始角和终止角为[π，1.8π]，半径为 5 mm；工件厚度 H=15 mm；广义电极丝半径R=0.18 mm；外补偿。仿真结果见图6和图7。

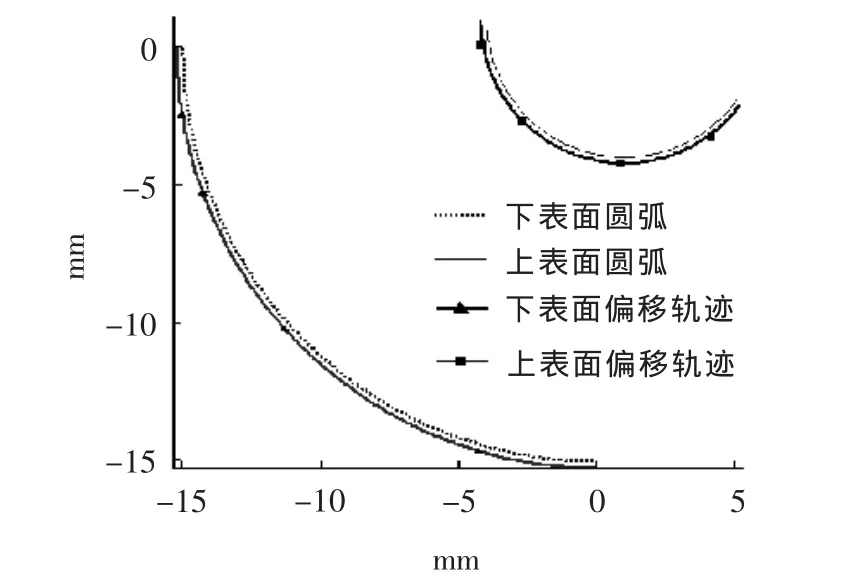
图6 上下表面均为圆弧的电极丝中心轨迹

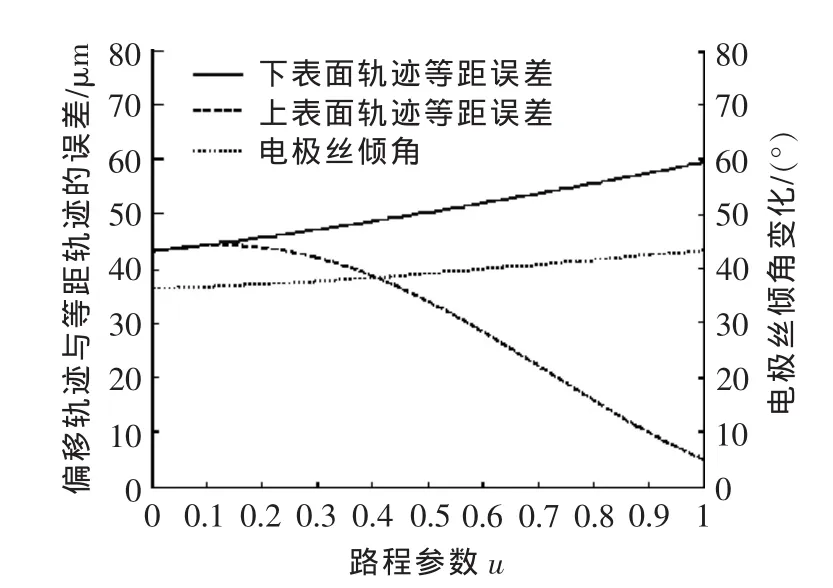
图7 上下表面均为圆弧的电极丝倾角变化及等距误差

从图6和图7可看出，电极丝的上、下表面中心轨迹都发生了“畸变”。如果采用传统方法做等距离偏移并加工，将导致下表面产生最大60 μm的误差，上表面产生最大45 μm的误差。

从上述3个仿真可看出，大锥度线切割加工时，利用广义电极丝模型方法求出的电极丝中心轨迹有着较复杂的变化，这种变化与加工轨迹本身的曲线特性、电极丝倾角和广义电极丝半径R有关，不能用简单的等距离偏轨迹移来替代电极丝的中心轨迹，否则会带来较大的编程误差和加工误差。

2 二次高分辨率采样方法线性化电极丝中心轨迹

利用广义电极丝模型方法可补偿大锥度加工时电极丝倾斜产生的椭圆度误差，并精确求出加工轨迹。通过上述仿真和分析得知，在修正误差后，大锥度线切割加工电极丝的中心轨迹是一个复杂的曲线，而目前的线切割控制软件只能实现对直线和圆弧的插补，必须找到一种方法，将电极丝中心轨迹曲线转换为能直接用于加工的线切割标准代码。

2.1 方法的分析

通过式（2）可知，当导线 C1(u)和 C2(u)方程已知，且广义电极丝半径R和工件厚度H值已知时，可通过代入路程参数u求出工件上、下表面的电极丝偏移轨迹曲线。如果将路程参数u足够细分，即采用高分辨率采样方法对上、下表面电极丝偏移轨迹曲线同时采样，那么，可将这对轨迹曲线线性化为多组“小直线对”的组合；如果采样分辨率足够高，那么，可保证连续的“小直线对”与上、下表面电极丝的偏移轨迹曲线之间的“逼近误差”足够小。同时，根据直纹面理论，对路程参数u进行同步采样，可保证上、下表面轨迹的同步线性化。

进一步，当加工所允许的最大逼近误差确定后，可用二次高分辨率采样方法确定“小直线对”的数目和每段小直线的起点和终点坐标。本文以下表面轨迹曲线为例，给出二次高分辨率采样方法的实现过程。从图 8 可看出，当初始点坐标为（X0，Y0），经过第一次高分辨率采样后，轨迹曲线离散化为（X0，Y0）…（Xi，Yi）（X1，Y1）（Xj，Yj）…（X2，Y2）…等一系列离散点的组合。采用初始点（X0，Y0）和任意一个离散点（X1，Y1）（当前离散点）所作的直线，可定义为“参考直线”。当确定参考直线后，从初始点开始按采样顺序计算初始点和当前离散点之间的所有离散点与参考直线的距离Δd，并与最大逼近误差σ作比较。如果每个Δd均小于最大逼近误差σ，则取下一个离散点（Xj，Yj）为当前离散点，并生成新的参考直线，然后重新从初始点开始按采样顺序计算初始点（X0，Y0）与（Xj，Yj）之间所有的离散点与新的参考直线之间的距离。当任意一个离散点与新的参考直线之间的距离满足Δd＞σ时，结束当前的计算工作，取（X0，Y0）为小直线的初始点坐标，上一个“当前离散点”（X1，Y1）为小直线的“结束点坐标”，形成加工代码。在下一个线性化周期，取上一个线性化周期的结束点（X1，Y1）为新的初始点坐标。重复上面的工作，可找到新的初始点所对应的新的结束点（X2，Y2）。重复上述方法，可找到轨迹曲线上的全部初始点及其对应的结束点，并生成对应的小直线。

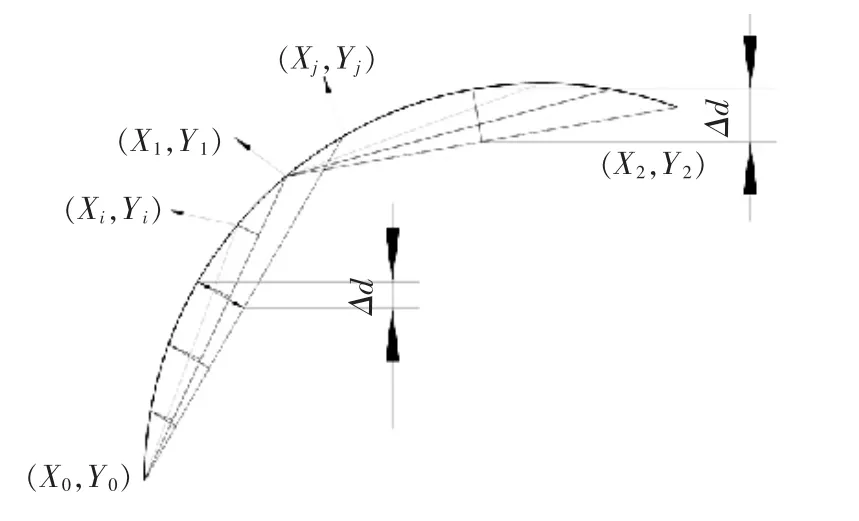
图8 二次高分辨率采样线性化方法流程图

针对大锥度线切割加工电极丝中心轨迹的线性化需要同时同步对上、下表面进行线性化的要求，通过同步对u高频次采样，可保证每个采样点的工件上、下表面的坐标与轨迹的总长度成正比，只是在判断“离散点”与“参考直线”之间的距离是否小于“加工所允许的最大逼近误差”时，多了一个判断条件，即任意一面有离散点满足Δd＞σ时，结束当前的采样和计算工作，取上、下表面当前线性化周期各自的“初始点坐标”和“结束点坐标”，形成一对加工代码对。

2.2 方法的实现

按上述分析给出“二次高分辨率采样方法线性化电极丝中心轨迹”的实现流程：

（1）读取上、下表面的一对原始加工代码（直线或圆弧），并根据设定的广义电极丝半径R及工件厚度H，用“广义电极丝模型”求出电极丝的中心轨迹曲线。

（2）根据原始加工代码的长度，选择适合的采样分辨率，并根据采样分辨率的值对路径参数u进行离散化，使路径参数的取值为u0…ui…ue。

（3）代入初始路径参数值u0，取得上、下表面轨迹线性化的第一对小直线的初始坐标；在此基础上，代入路径参数u1、u2和u3并计算坐标值。根据u0和u3的坐标值形成上、下表面两条小直线，可计算u2点坐标值（x2，y2）（u2，v2）到各自小直线的距离 Δd1和Δd2，并判断是否大于逼近误差σ。如果其中任意一个大于σ，则选择u2点的坐标为结束坐标，形成第一个小直线对；如果Δd1和Δd2都小于σ，则初始化u4的坐标，形成u0和u4的直线，并依次计算u1、u2、u3点到该直线的距离。如果其中任意一个大于σ，则选择u3点的坐标为结束坐标，形成第一个小直线对。

（4）按步骤（3）给出的方法，找到第一个满足“Δd1i和Δd2i其中一个值大于σ”的路径参数离散点ui，取ui-1的坐标值为第一个“小直线对”的结束坐标值，形成第一个小直线对。

（5）取ui-1的坐标值为下一个小直线对的初始坐标值，按步骤（3）～（4）给出的方法，找到结束坐标值，形成新的小直线对。

（6）按步骤（3）～（5）的方法完成上、下表面轨迹的线性化工作，形成小直线对的组合，并形成对应的加工代码。

3 方法的验证与仿真

采用二次高分辨率采样方法线性化电极丝中心轨迹，并对上述3个仿真结果进行进一步的仿真验证。

针对仿真1，设定最大逼近误差为0.5 μm，仿真结果见图9。可看出，上、下表面线性化为7个小直线对，上、下表面的小直线一一对应，且轨迹同步，与理论轨迹的逼近误差小于0.5 μm。

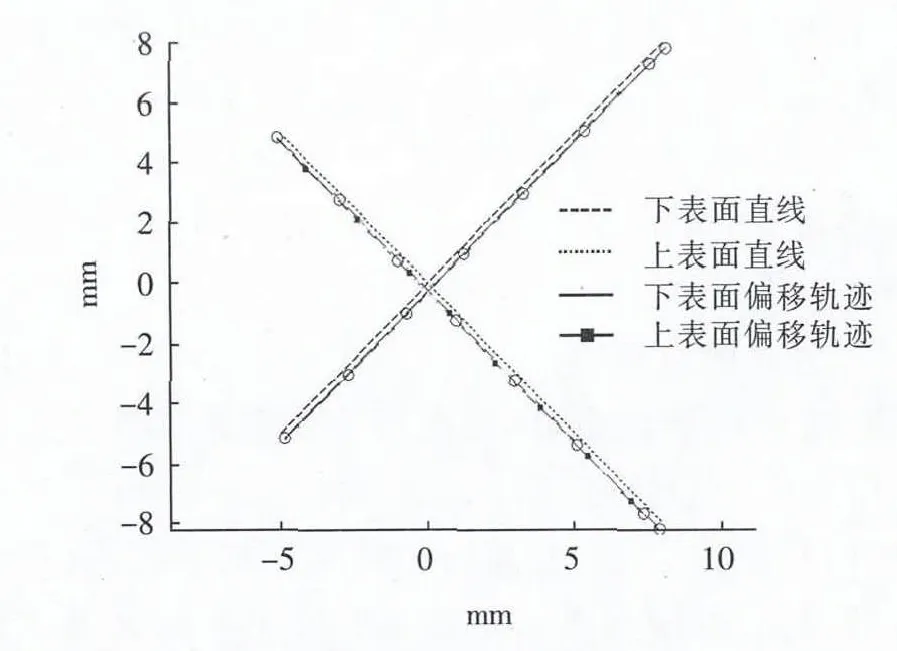
图9 上下表面均为直线的电极丝中心轨迹线性化

针对仿真2，设定最大逼近误差为2 μm，仿真结果见图10。可看出，上、下表面线性化为30个小直线对，上、下表面的小直线一一对应，且轨迹同步，与理论轨迹的逼近误差小于2 μm。

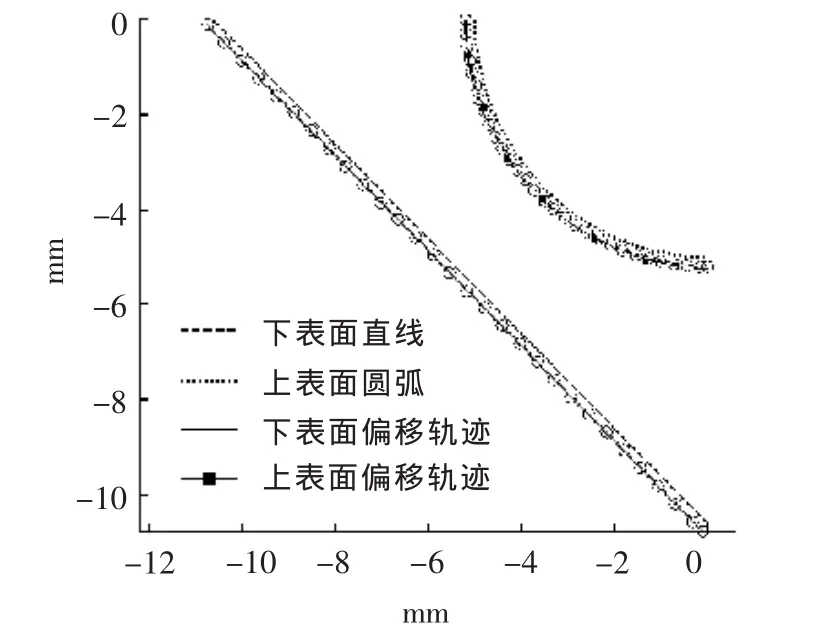
图10 下表面直线、上表面圆弧的电极丝中心轨迹线性化

针对仿真3，设定最大逼近误差为2 μm，仿真结果见图11。可看出，上、下表面线性化为51个小直线对，上、下表面的小直线一一对应，且轨迹同步，与理论轨迹的逼近误差小于2 μm。

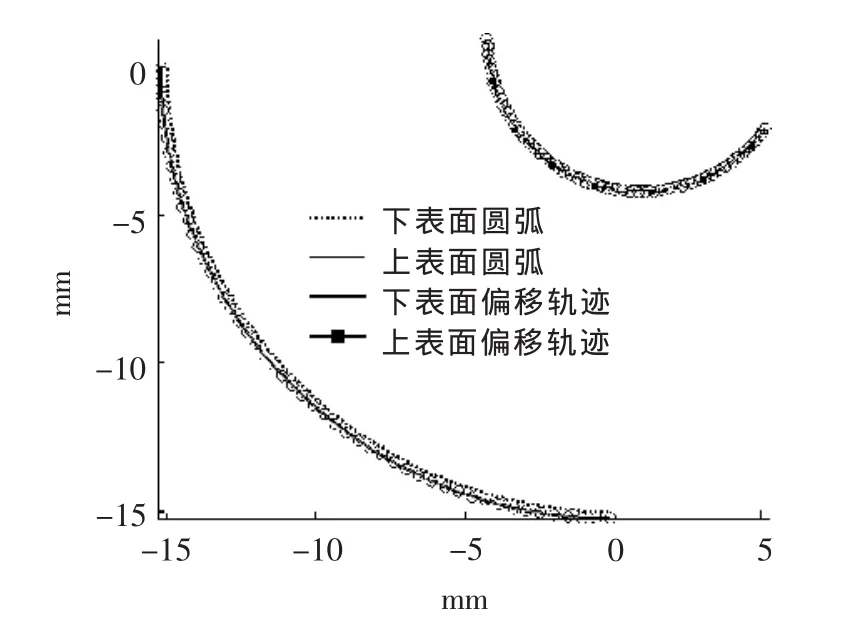
图11 上下表面均为圆弧的电极丝中心轨迹线性化

4 结论

本文介绍了使用“广义电极丝模型”方法求取大锥度线切割加工时工件上、下表面电极丝的中心轨迹，用MATLAB实现了该方法并给出了3个仿真实验。结果表明，大锥度加工时，电极丝中心轨迹与工件上、下表面的加工代码、工件厚度H和广义电极丝半径R均有关，是一个复杂的非规则曲线，不能用原始加工代码做等距离偏移来替代，否则会产生较大的替代误差。

为此，本文提出用“二次高分辨率采样方法”线性化电极丝中心轨迹。理论分析和仿真结果表明，用该方法能将大锥度加工电极丝中心轨迹的非规则曲线线性化为“多组小直线对”，并将逼近误差控制在加工精度要求所设定的范围内，线性化后的“小直线对”可直接用于锥度线切割加工。

[1] 周坚.线切割锥度加工电极丝水平截面的椭圆度误差及补偿[J].电加工，1991（6）：9-13.

[2] Lee Y S，Koc B.Ellipse-offset approach and inclined zig-zag method for multi-axis roughing of ruled surface pockets[J].Computer-Aided Design，1998，30（12）：957-971.

[3] 李论，赵万生，王刚，等.用椭圆偏置法计算线切割直纹面加工的电极丝中心轨迹[J].电加工与模具，2001（2）：35-38.

[4] 翟洪军，任艳芳，刘正埙.复杂直纹面加工中电极丝中心轨迹的求取算法研究 [J].电加工与模具，2004（4）：23-26.

[5] 翟红军，汪炜，安鲁陵，等.电火花线切割加工中上下异形体轨迹合成的同步线性化 [J].电加工与模具，2003（6）：25-27.