微细电火花放电通道扩展的研究
朱凯,王春梅,张怡茹,褚旭阳
(厦门大学物理与机电工程学院,福建厦门361005)
微细电火花放电通道扩展的研究
朱凯,王春梅,张怡茹,褚旭阳
(厦门大学物理与机电工程学院,福建厦门361005)
为了模拟微细电火花放电通道扩展的过程,对放电等离子体通道进行了深入研究,建立了一个适用于微细电火花放电加工的等离子体扩展模型。基于介质击穿机理和磁流体力学的相关知识,模型综合考虑了等离子体扩展过程中的粘性力、表面张力及磁场箍缩力等各个作用力,使扩展过程更接近于真实。最后,通过比较微细电火花RC单脉冲放电的模型计算直径与实际加工直径,验证了等离子体扩展模型的正确性。
微细电火花加工;RC脉冲;磁流体力学;等离子体模型
微细电火花加工作为微制造领域的精密加工方法之一,拥有非接触加工、宏观作用力小等特点,在航天航空、微型模具制造、生物医疗仪器等行业发挥着重要作用。在电火花加工过程中,放电能量是通过放电通道来传输的,而放电通道的形成、扩张和消散将直接影响加工效果。因此,对于放电通道的研究十分必要。
电火花放电过程在空间和时间上都高度集中,同时涉及了电磁学、电动力学、热力学和流体动力学等多门学科,放电过程的理论研究较困难。20世纪70年代初,一些学者就尝试建立等离子体通道的数学模型。Eubank运用流体动力学方程、能量平衡方程、辐射方程及等离子体状态方程,建立了一个变质量圆柱等离子体模型[1],为等离子体通道的研究提供了一个新方向;在此基础上,Sandeep运用新型击穿理论得到放电初始条件,同时考虑了放电过程中的粘性力和表面张力,从而建立了新的等离子通道模型[2]。前人的理论对推动等离子通道扩张机制的发展做出了巨大贡献,但微细电火花加工相对传统电火花加工具有放电时间短、放电能量小的特点,因此,前人在建立等离子体扩展模型过程中简化的条件(箍缩磁场力、粘性力和表面张力等扩张作用力)都是不容忽视的。
本文综合考虑了放电过程中的各个因素,建立了适合微细电火花加工的等离子通道模型,计算出了放电通道时变的半径、压强和温度,并在相同的加工条件下进行了微细电火花放电加工实验,将实验数据与理论仿真结果进行了比较。
1 等离子体模型
在微细电火花放电过程中,电子高速向正极运动并撞击工作液介质中的分子或中性原子,产生碰撞电离,从而在两极之间形成一个等离子体通道。整个过程可分为击穿、扩张、消电离3个阶段。
1.1 等离子体击穿模型
早期建立的模型主要是基于气泡机制的,研究认为在击穿过程的初始阶段,气泡是由电极尖端周围的液体受热气化形成的,当气泡不断扩张达到一定阈值就会引起放电[3-4]。基于气泡机制的击穿时间通常在微秒级别,而微细电火花RC脉冲放电一般都在纳秒级别,液体中放电通道的扩张速度在104~105m/s[4],简单的气泡动力学扩张机制不足以解释微细加工的快速放电。因此,Sandeep将气泡机制和电子机制相结合,建立适合微细电火花加工的等离子体击穿模型[2],较符合实际情况。在该击穿模型中,负极首先产生成核气泡,由于气泡的扩张,局部介电质密度逐渐降低;当气泡到达电子撞击标准时,立即引发电子碰撞电离,完成击穿。
本文在分析了微细电火花RC脉冲放电的击穿机理后,决定采用Sandeep的击穿模型,并计算出气泡在扩张到电子激活状态并即将进入等离子体扩张阶段时的初始半径ra、初始压力Pa、初始温度Ta,这些初始条件将被运用到等离子体扩张模型中。
1.2 等离子体扩张模型
虽然等离子体扩张模型在能量平衡方面不断被修正和完善,但建模过程中往往忽略了绝缘介质的粘性力、表面张力及磁箍缩力等作用力。特别是在微细电火花加工中,等离子体有着较快的扩展速度和较强的爆发力,放电过程中的这些作用力是不能忽略的。因此,本文将建立一个适用于微细电火花RC脉冲放电的等离子体通道扩展模型。如图1所示,等离子体的上下两端被工件和工具电极限制,而工件和电极被认为是两个相互平行的刚性边界,它们之间的距离被定义为放电间隙。等离子体的径向被液体放电介质所包围,在其界面上作用着各种约束力。

图1 等离子体通道扩张
(1)磁流体动力学方程
在放电过程中,等离子体通道内部压强变化幅度大、过程短,通常将其视作不可压缩流体。因此,通道边界层的Navier-Stokes方程可缩写为:
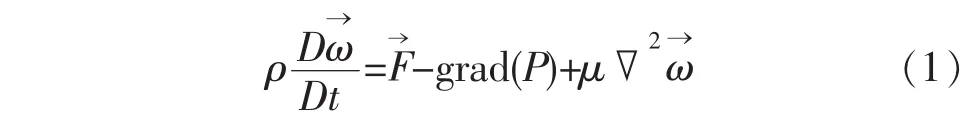
式中:▽2为Laplace算子,;μ为粘性系数;t为时间。
其中,体积力F为放电过程中等立体边界受到的各种径向力。磁场箍缩力就是体积力的一种,它是由等离子体内的电流束相互作用而引起的。通道半径越小、电流越大,等离子体柱受到的径向箍缩作用力就越大。因此,在微细电火花加工中,磁场箍缩力不容忽视。假设等离子体通道半径为a,柱内电流密度为j(r)、磁感应强度为B(r)、压强分布为P(r),μ0为磁导率,则麦克斯韦方程在柱坐标系中可表示为:
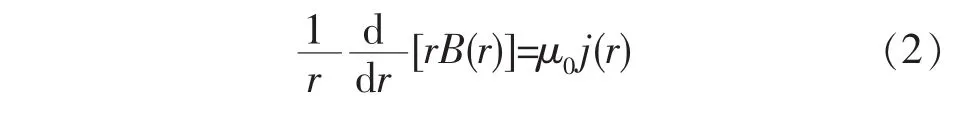
由上式解得等离子体内的磁场分布为:

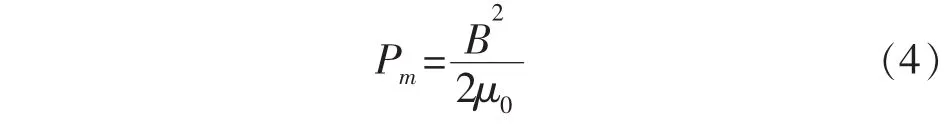
由于微细电火花放电等离子体通道很窄,可假设通道内部的电流密度j是均匀分布的,那么,等离子体内的磁场分布式(3)可简化为:

式中:I为放电电流;a为等离子体通道半径。
将式(5)代入磁压强表达式(4),可得磁压强在通道半径a内的分布式:

为便于模型的计算,本文通过式(6)求得半径为a的等离子通道内平均磁压强表达式为:

由于等离子体通道只在径向扩张,可将式(1)化简成柱坐标形式:

式中:vr为径向扩展速度;Pr为径向压强;Fr为径向体积力。
考虑液体表面张力S,由上述分析可得某一时刻体积力的表达式:)

在等离子体通道外选择点f作为参考点,rf为点f到等离子体中心的距离,Pf为参考点f的压强(图2)。因此,等离子体通道扩展的流体动力学方程为:
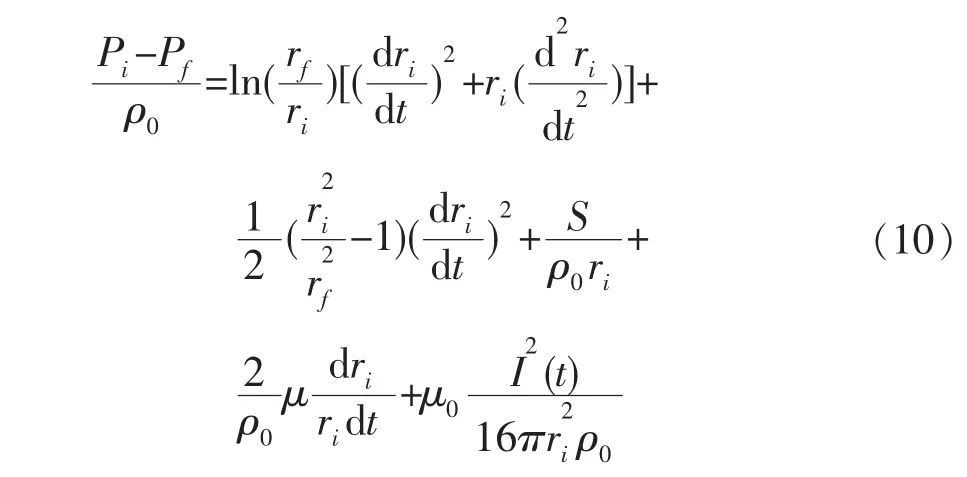
式中:ri为等离子体半径;ρ0为液体介质的密度;Pi为等离子体内部压强;I(t)为时变放电电流。

图2 等离子体截面图
式(10)全面表达了等离子通道扩张的流体动力学,包含了液体边界的粘性力、表面张力和磁场箍缩力。从式(10)可看出,要求解扩张方程,必须得到每个时刻等离子体通道内部的压强。下文通过一系列传热方程及等离子体理论知识计算求得内部压强。
(2)能量平衡方程
由上述流体动力学分析可看出,分配到等离子体通道的能量主要用于克服粘性力、表面张力、磁场箍缩力及液体介质的汽化和相关焓变。其中,克服粘性力、表面张力和箍缩力所消耗能量的表达式为:

由于微细电火花加工脉冲时间在微秒甚至纳秒级别,对于周围流体介质无法在这么短的时间内通过传导和对流进行热传递,忽略由传导和对流所损失的部分能量后,热辐射成为主要的能量传递机制。假设等离子体通道作为一个黑体,液体介质汽化和分解的有效能量表达式[1]为:
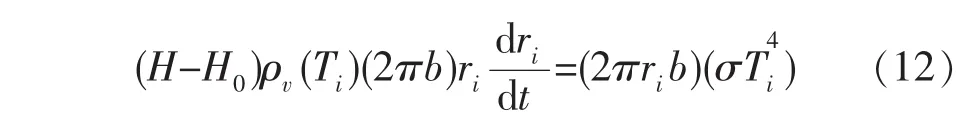
式中:σ为Stefen-Boltzmann常数;H为等离子体的热焓;H0为液体介质的热焓;b为加工间隙;Ti为等离子体温度;ρv为气态密度。
Eubank等[1]在分析等离子体扩张过程的能量平衡时,只考虑了液体介质气化和相关焓变的能量,未考虑到克服粘性力、表面张力和磁场箍缩力所消耗的能量。本文通过对等离子体通道受力的分析,增添了这部分能量,完善了等离子体通道扩张时的能量分配机制。因此,分配到等离子体通道的能量可表达为:

(3)电离方程
等离子体可看作一种导电流体,当外部施加能量时,物质就会被离解成正、负电荷状态。在外加电压作用下,电子、离子流动而产生电流。对于电子只与每个电荷数为Z的带电粒子碰撞的情况,整体等离子体电导率为:
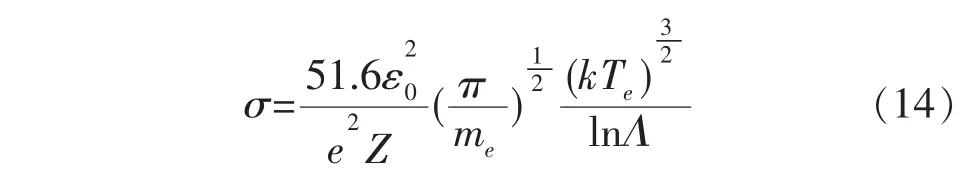
式中:lnΛ为库伦对数;ε0为真空介电常数;k为玻尔兹曼常数;Te为电子温度;σ为Spitzer电导率;e为电子电荷;me为电子质量。
在放电产生的高温高压等离子体中,电流密度J与粒子平均漂移速度vd和粒子密度N成正比,即J=evdN。利用迁移率μ,可将漂移速度写成简单正比于电场的形式:
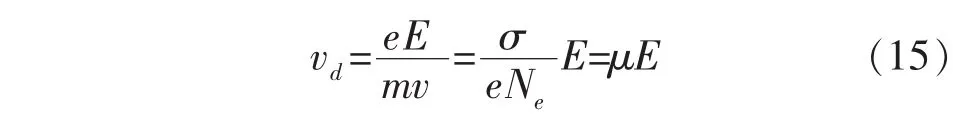
式中:m为单个介质分子质量。
由式(15)可推出电导率与电场强度、电流密度的关系:

将Spitzer电导率公式(14)与相关参数值代入式(16)得:

等离子体通道实际上是高温电离气体,假设单一电离,可近似Ni=Ne,则等离子体动压强公式为:

式中:Ni为离子密度;Ne为电子密度。
1.3 扩展模型的计算流程
将等离子体的扩张方程、能量方程和压强方程综合起来,建立了等离子体扩展的计算模型。该模型的计算流程为:
(1)运用放电参数和击穿阶段的理论公式,计算出等离子体扩张阶段的初始条件;利用这些初始条件和等离子体径向扩张方程[式(10)]可计算出每一迭代步的等离子体通道半径。
(2)结合该通道半径和电介质的物性参数,利用能量守恒方程[式(12)]计算出该时间步结束时等离子体的温度。
(3)使用该时刻的温度,利用电离方程和压强方程[式(17)、式(18)]计算出该时间步结束时等离子体的电子密度和压强。
(4)将计算出的压强代入等离子扩展方程,作为下一个时间步的初始条件继续计算。通过不断迭代计算直到放电时间结束,就能得到放电过程中等离子体通道的半径、温度和压强曲线。
2 等离子体扩展模型的验证
由于微细电火花放电过程的复杂性、快速性,放电通道的扩张过程极难被观测到,因此,很难获得放电过程中等离子体通道的半径。Nagahanumaiah等通过光谱学的方法观测等离子体通道半径[5],但该方法被很多学者认为是不能准确观测到等离子体通道半径的。现代学者普遍认为放电凹坑的直径就是放电通道的最终直径,通过测量各个参数下的放电凹坑形貌来获得放电经验公式,并依靠经验公式来计算放电凹坑直径,从而间接获得放电通道的直径[6-8]。基于前人的研究,本文认为等离子体通道半径与放电凹坑半径应该是不相等的,但增长的趋势应该是一致的,从而得出了验证上述已建模型的方法。为了验证上述模型是否正确,本文不但运用已建的通道扩展模型计算了不同放电条件下的通道直径,还进行了相应的微细电火花RC脉冲放电加工实验,并借助扫描电镜获得放电凹坑的直径;同时,与理论计算所得的等离子体通道直径进行增长趋势的对比,分析验证模型的正确性。
2.1 模型的计算
微细电火花加工在煤油介质中进行,由于煤油组成的复杂性,实际的热物属性难以确定。于是,本文选用煤油的主要成分烷烃来代替煤油进行计算。在放电间隙和放电电容一定的条件下,利用等离子体模型计算了不同电压下放电通道的扩展情况,计算结果见图3。放电条件如下:放电电压40~100 V,放电电容10 000 pF,时变电流由采集得到。
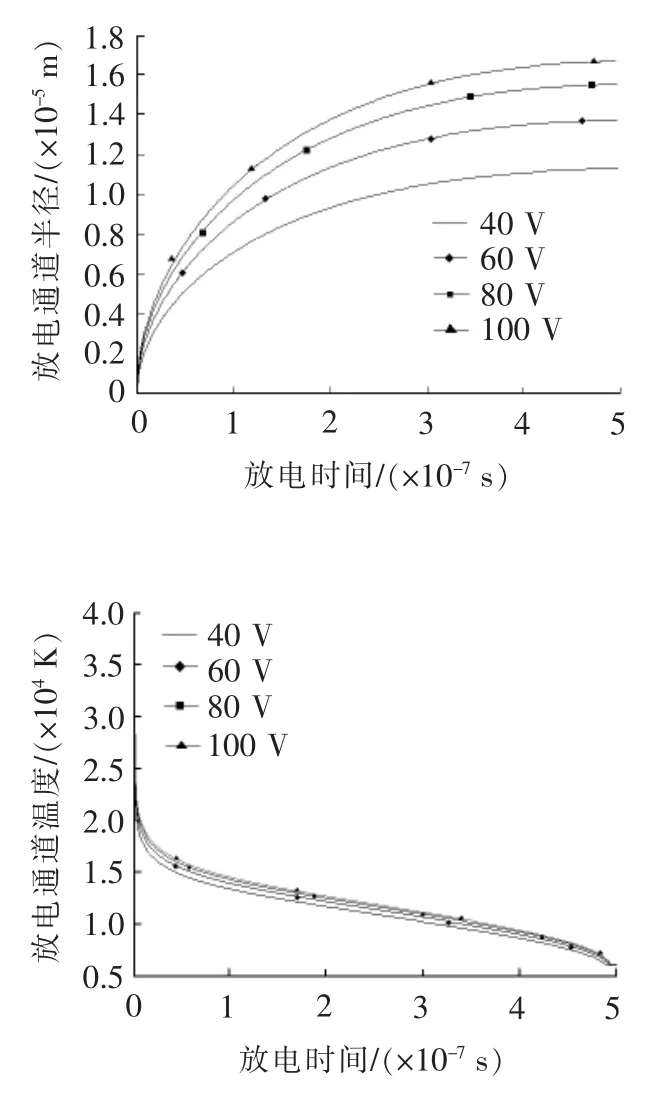
图3 10 000 pF时不同电压对等离子体的影响
2.2 单脉冲放电实验
本文还进行了与上述计算条件相同的微细电火花加工实验,通过比较RC脉冲放电产生的凹坑直径与理论计算所得的等离子体通道直径,验证模型的正确性。
(1)实验设备
实验在自行研制的微细电火花加工装置上进行,该装置的Z轴采用直线电机驱动,用0.05μm光栅尺作为反馈元件,且能实现高精度全闭环控制。加工电源采用RC式脉冲电源,放电电压可在0~300 V范围内调节,电容可在1000~20 000 PF范围内调节。绝缘介质为煤油,电极材料为黄铜,工件材料为钛合金。用Tektronix TPS2014示波器采集电压,用Tektronix TCPA300电流检测设备采集电流。参照计算模型所使用的参数,进行了不同放电电压的加工实验,加工参数见表1。

表1 加工参数
(2)实验结果
图4是利用XL30ESEM扫描电镜获得的放电凹坑形貌。可见,工件表面形成了碗状的蚀坑,在碗状蚀坑内部有一些残余的碎屑未被抛蚀。随着放电能量的增加,蚀坑直径显著增大,与理论分析一致。

图4 凹坑形貌
2.3 模型评估
蚀坑直径与等离子体模型理论计算的放电通道直径的比较结果见图5。可看出,理论计算的通道直径与实验凹坑直径随电压的增长趋势是一样的,这和上文分析的结果一致。从数值上来看,理论计算的通道直径比实验获得的放电凹坑直径大,这是因为热源是高斯分布的,加载到工件上的热源主要集中在小于热源半径的范围内,导致工件上受热作用的范围必然小于热源半径。因此,实验结果可验证已建的等离子体通道模型是可行的。

图5 不同电压下的理论计算与加工实验对比
3 结论
(1)在击穿阶段,本文采用了气泡机制和电子机制相结合的击穿机制。该机制更符合微细电火花加工中时间短、能量密度大等特点,可解释放电过程中的众多现象。
(2)在等离子体扩张阶段,本文基于磁流体力学和边界层理论,综合考虑了放电过程中的各个放电力(如磁场箍缩力、表面张力和粘性力),并推导了磁场箍缩力的计算公式。通过对这些放电力的推导和添加,完善了等离子体扩张模型,并通过比较理论计算的通道直径与加工实验所得的凹坑直径,验证了模型的可行性。
(3)在模型计算阶段,将实验采集的时变放电电压和放电电流应用到理论计算模型中,可增加模型的计算精度。加工实验结果表明,该计算模型能很好地仿真等离子体通道的扩展情况。
[1]Eubank P T,Patel M R,Barrufet M A,et al.Theoretical models of the electrical dischargemachining process.Ⅲ. The variablemass,cylindrical plasmamodel[J].Journal of Applied Physics,1993,73(11):7900-7909.
[2]Dhanik S,Joshi S S.Modeling of a single resistance capacitance pulse discharge in micro-electro dischargemachining[J].Journal of Manufacturing Science and Engineering,2005,127(4):759-767.
[3]Watson P K,Chadband W G,Sadeghzadeh-Araghi M. The role of electrostatic and hydrodynamic forces in the negative-point breakdown of liquid dielectrics[J].IEEE Transactions on Electrical Insulation,1991,26(4):543-559.
[4]Beroual A.Electronic and gaseous processes in the prebreakdown phenomena of dielectric liquids[J].Journal of Applied Physics,1993,73(9):4528-4533.
[5]Nagahanumaiah,Ramkumar J,Glumac N,et al.Characterization of plasma in micro-EDM discharge using optical spectroscopy[J].Journal of Manufacturing Processes,2009,11(2):82-87.
[6]Marafona J,Chousal J A G.A finite element model of EDM based on the Joule effect[J].International Journal of Machine Tools and Manufacture,2006,46(6):595-602.
[7]Zhang Y,Liu Y,Shen Y,etal.A new method of investigation the characteristic of the heat flux of EDM plasma[J]. Procedia CIRP,2013,6(7):450-455.
[8]Erden A.Effect ofmaterials on themechanism of electric discharge machining(EDM)[J].Journal of Engineering Materials and Technology,1983,105(2):132-138.
Study on Expansion of M icro-EDM Discharge Channel
Zhu Kai,Wang Chunmei,Zhang Yiru,Chu Xuyang
(SchoolofPhysicsandMechanical&ElectricalEngineering,Xiamen University,Xiamen361005,China)
To simulate the process ofmicro-EDM discharge channel expansion,discharge plasma channel has been studied.A suitable plasma expansion model of micro-EDM has been established. Based on the dielectric breakdown mechanism and relevant knowledge of MHD,the various forces such as viscous force,surface tension and magnetic pinch force,in the process of plasma expansion has been considered,which makes the expansion process closer to the real.Finally,comparing the calculation diameter of micro-EDM RC single pulse discharge model with the actual machining diameter,the correctness of plasma expansionmodel is verified.
micro-EDM;RC pulse;MHD;plasmamodel
TG661
A
1009-279X(2015)03-0021-05
2015-01-13
朱凯,男,1989年生,硕士研究生。

