用于六轴联动数控电火花加工的广义单位弧长增量插补法

陈 默，陈 昊，奚学程，赵万生

（上海交通大学机械与动力工程学院，上海200240）

随着航空航天工业的不断发展，对含有复杂形状型腔的零件（如航空航天发动机中的闭式整体叶盘类零件）加工的需求日益旺盛，其加工通常需要工具电极相对于工件沿着复杂轨迹运动。近年来，在切削加工领域中，参数曲线以其数据量小、平顺性高的优点，越来越多地被用于复杂轨迹的描述，许多学者针对参数曲线的插补方法做了研究[1-4]，主流商用数控系统厂商（如Siemens、FANUC）也纷纷推出了具有参数曲线插补功能的数控系统[5-7]。这些插补方法大多属于针对切削加工而改进的数据采样法，根据曲线局部特性和机械系统限制来对曲线进行粗插补，生成一系列直线段并规划尽可能高的运动速度，由此会造成粗插补采样间距较大，导致粗插补与精插补的总误差比脉冲增量法大[8]。

与切削加工不同，电火花加工是一种慢速、且进给速度难以事先规划的运动。因此，脉冲增量法比数据采样法更适合电火花加工轨迹插补[9-10]。但脉冲增量法可插补的曲线类型十分有限，现有电火花成形加工机床数控系统的运动轨迹插补指令大多仍采用直线或圆弧指令来给出，而对于参数曲线描述的复杂运动轨迹的插补法的研究和应用还不多。李志勇[11]提出了用于多轴联动电火花加工的Huffman树插补器和DDA插补器；黄海鹏[10]和刘丽丽[12]将运动轴进行两两逐层组合，再借助平面曲线插补法二轴联动的思想实现多轴联动插补，并提出了可逆插补算法以实现反向插补。但上述方法仅能实施直线和圆弧的插补，对于一般参数曲线的插补还难以胜任。此外，研究人员还提出了针对电火花铣削加工的参数曲线插补器[13-15]，丰富了电火花加工运动可插补轨迹的种类，但还不能直接用于多轴联动电火花成形加工所需直线轴与旋转轴的同步插补。

为解决曲线同步插补的问题，本研究团队基于脉冲增量法中的数字积分法的思想，提出了单位弧长增量法，并将其运用于线切割上下异形面的加工轨迹插补中[16]。本文在此基础上，进一步将单位弧长增量法推广到六轴联动电火花成形加工中，提出了广义单位弧长增量法，实现了复杂参数曲线的正反双向插补及直线轴与旋转轴的联动插补，并通过仿真和加工实验进行了验证。

1 多轴联动参数曲线轨迹插补原理

1.1 参数曲线的正反双向插补法

在传统的电火花加工机床数控系统中，加工轨迹多以直线和圆弧来描述。脉冲增量插补法具有对直线和圆弧进行直接精插补的能力，且精度比一般的数据采样法高。脉冲增量插补法中较常用的有逐点比较法、最小偏差法和数字积分法。分析这些方法对直线和圆弧的插补原理可知，逐点比较法和最小偏差法的思想是计算插补点与理想曲线之间的位置偏差，根据位置偏差的符号或大小来选取下一步的插补点，是偏向于轮廓误差控制的插补法；数字积分法的本质是计算理想曲线某点的一定长度的切线段在各坐标轴上的投影长度，通过判断各轴长度累计的状况来决定轴是否进给，是一种偏向于插补进度控制的插补法。

电火花加工是一种需不断调整工具电极与工件之间间隙的、有进有退的运动过程，而进给方向上的间隙与运动轨迹的插补进度直接相关。因此，基于插补进度控制的数字积分插补法与其他脉冲增量法相比，更便于实现进给方向上的间隙调整。然而，运用数字积分法虽然解决了进度控制的问题，但还要考虑如何限制轮廓误差。对于直线插补，数字积分法可将轮廓误差限制在1个脉冲当量（Basic Length Unit，BLU）以内；对于圆弧插补，数字积分法采用1 BLU长度的切线代替1 BLU长度的弧线来递推下一插补点的坐标，从微积分的角度来看，相当于将各轴插补点坐标的递推式以泰勒公式展开至一阶：

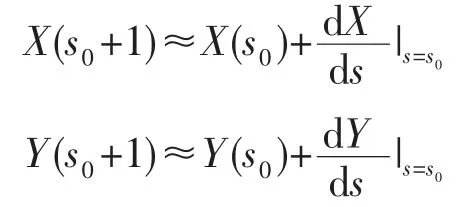
式中：s为弧长参数；（X(s)，Y(s)）T为参数 s处的插补点坐标。

需要反向插补时，只需将一阶导数项前的正号变为负号即可。然而，一阶泰勒展开式的截断误差较大，在插补一段距离后，坐标计算误差逐渐累积，插补点会逐渐且明显地偏离理想圆弧（图1a）。为解决该问题，单位弧长增量法将各轴插补点坐标的递推式以泰勒公式展开至二阶甚至更高阶（以X轴为例）：

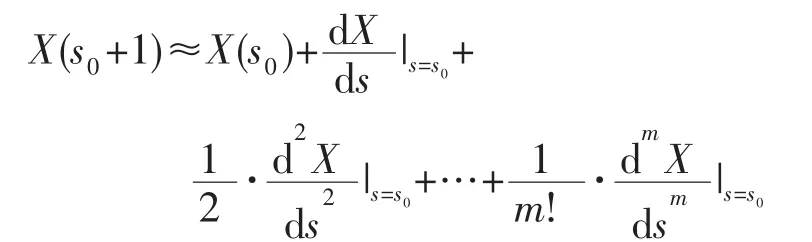
通常只要取展开阶数m=2，就能明显降低泰勒展开式的截断误差，从而提高圆弧插补的轮廓精度（图1b）。对于直线和圆弧的插补，单位弧长增量法和其他脉冲增量法一样，能避免浮点数运算[16]。

圆弧是非常特殊的参数曲线，拥有良好的几何性质，使坐标递推泰勒展开式的截断误差与坐标增量相比很小，因此，依靠提高泰勒展开的阶数就能很好地降低轮廓误差。然而，对于复杂形状零件的加工轨迹（如多轴联动电火花成形加工的轨迹），当采用参数曲线代替小直线段来描述轨迹时，往往选用灵活性较大的B样条曲线或NURBS（Non-Uniform Rational B-Splines）[17]。 但使用 NURBS 存在的问题是：由于复杂轨迹参数曲线的切矢量和曲率变化多样，故无法确定坐标递推泰勒展开式的截断误差大小。由于每步使用坐标递推泰勒展开式都会引入新的截断误差，该误差将随着插补的进行而一直累计下去，使推算的坐标值偏差越来越大，轮廓误差难以控制。

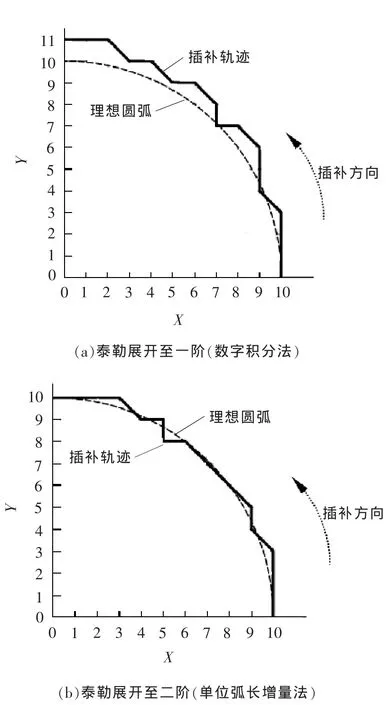
图1 泰勒展开阶数对插补误差累积的影响

要限制坐标值误差的累积，就要从递推方法上做出改变。设三维空间中的一条参数曲线的表达式为 P(u)=（X(u)，Y(u)，Z(u)）T。 对于一般的非圆参数曲线，不再采用类似于数字积分法插补圆弧时的“坐标递推”方式，而改为采用数据采样法粗插补阶段的“参数递推”方式。也就是说，不是由坐标泰勒展开式

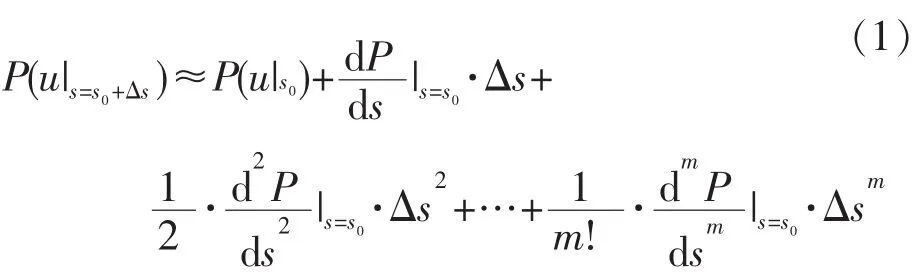
去递推下一插补点坐标（图2a），而是先递推出曲线P(u)在下一插补点的参数值 u｜s=s0+Δs后，再将 u｜s=s0+Δs代入 P(u)表达式中，求出 P(u｜s0+Δs)（图 2b）。 与坐标递推类似，参数递推也是一种近似计算，常见的方法有泰勒展开法、龙格-库塔法、预估-校正法等[18]。采用二阶泰勒展开法进行参数递推时，有：

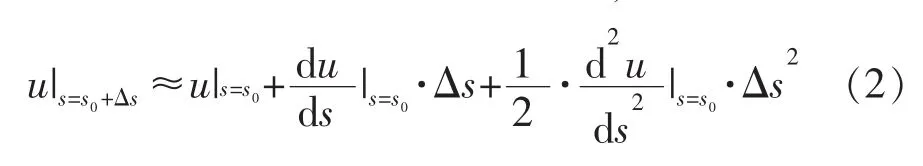
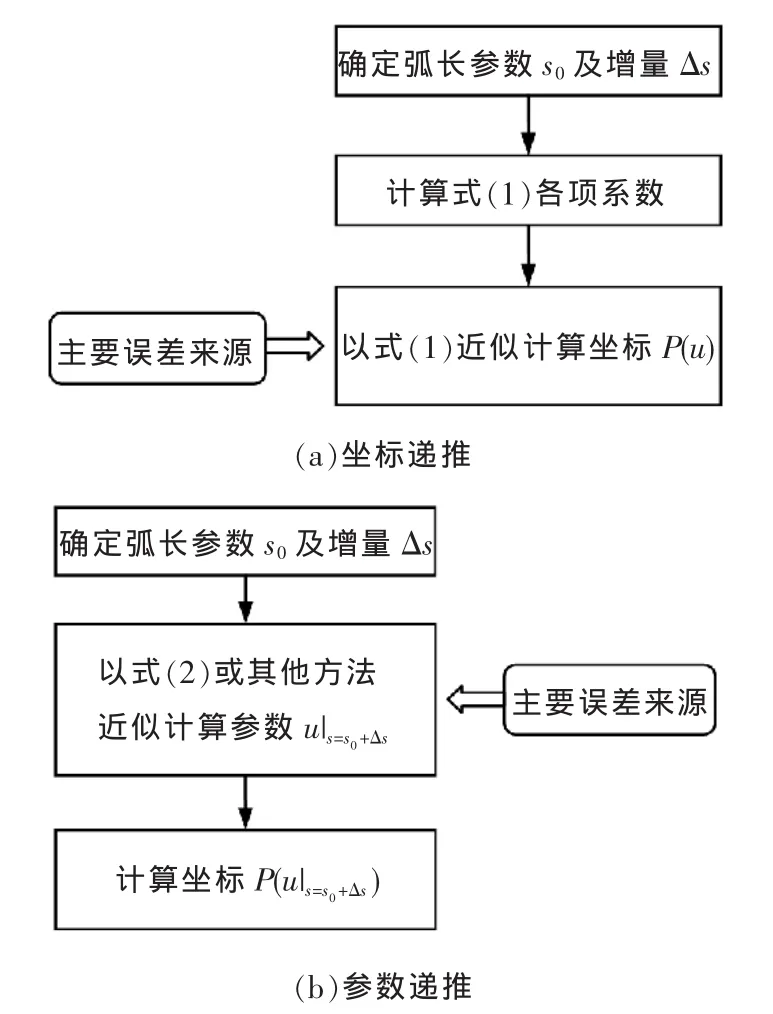
图2 两种递推方式的区别

把对坐标的近似计算改为对参数的近似计算后，插补误差的来源便从坐标递推式转移到了参数递推式中，这样能保证每步递推所得的坐标值均落在曲线P(u)上，使插补点处的轮廓误差≤1 BLU。然而，数据采样法粗插补的缺陷在于其弧长增量值Δs是不确定的，有时远大于1 BLU，导致在相邻采样点之间的弦线上运动时，仍有可能与理想曲线P(u)偏离较大，即引起较大的弓高误差。为解决这一问题，单位弧长增量法取定每步沿曲线进给方向的弧长增量Δs=1 BLU，这时只要参数递推足够精确，就能保证每步进给的曲线段在每个轴上的投影都≤1 BLU，达到和脉冲增量法类似的精插补效果，使每个生成的插补点都能经四舍五入圆整为以BLU为单位的整数后直接作为精插补结果、直接生成进给脉冲（图 3）。

将式（2）代入 P(u)，并取 Δs=1 BLU，可得曲线弧长参数s=s0处正向递推s=s0+1处的插补点的公式：

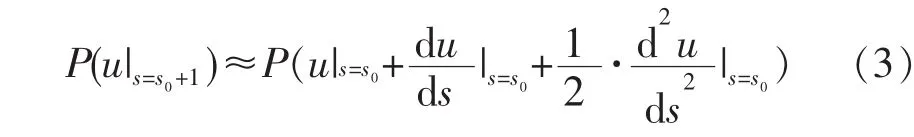
对于反向插补，Δs=-1 BLU，即由曲线弧长参数s=s0处反向递推s=s0-1处的插补点的情形，只需将式（3）右侧泰勒展开式中的一阶项符号变为负号：

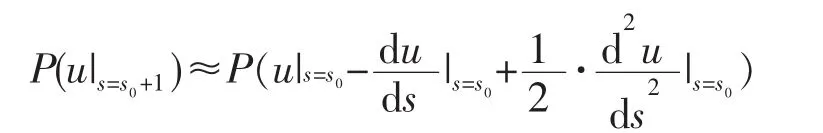
由此可见，单位弧长增量法能灵活实现沿参数曲线轨迹的正反双向插补，有利于实现电火花成形加工中的短路回退、抬刀、暂停/退刀等需沿原路径精确回退的特殊功能。

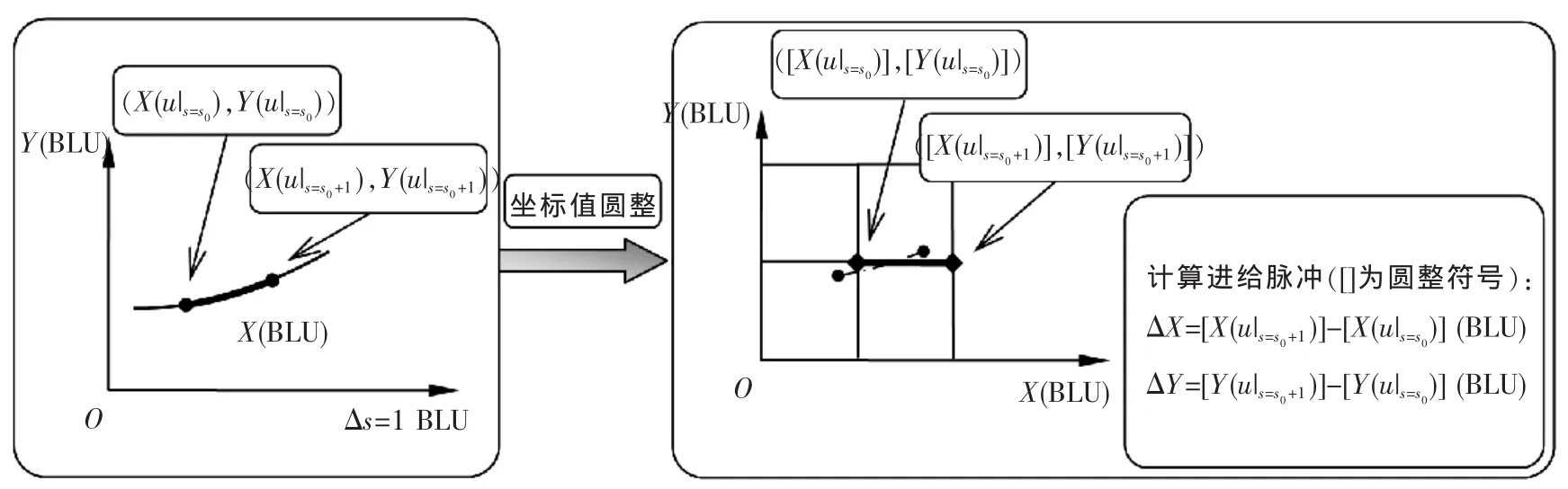
图3 单位弧长增量法的直接精插补

1.2 直线轴与旋转轴同步运动的实现

多轴联动电火花成形加工包含直线轴和旋转轴的同步运动，但直线轴通常使用长度单位mm，旋转轴通常使用角度单位 °。因此，要实现同步，首先需实现单位的统一，方法是将插补指令的各轴坐标分别乘以各自的分辨率，化为以BLU为单位的坐标值。以A轴为例，设其分辨率为1000 counts/°，则有1 count=1 BLU=0.001°；此时，若A轴的当前坐标值为5.5°，则A轴的当前坐标值可表示为5.5×1000=5500(BLU)。在下文中，各轴坐标值和各个弧长值均以BLU为单位。

多轴联动运动轨迹可采用不同的方式进行描述，依加工需求、数控系统解释器规定和CAM系统对轨迹的表示形式而定。在传统的多轴联动加工机床数控系统中，一般只处理G01直线指令，也就是各轴运动之间互为线性关系的情况（以六轴为例）：

式中：(Xs,Ys,Zs,As,Bs,Cs)T=F(us)和(Xe,Ye,Ze,Ae,Be,Ce)T=F(ue)分别为G01指令的起点坐标和终点坐标；us和ue分别为起点参数值和终点参数值。为了简化描述，分别记 X=x1、Y=x2、Z=x3、A=x4、B=x5、C=x6， 则式（4）可简单表达为：

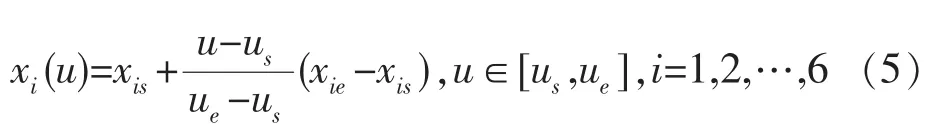
在描述多轴联动加工闭式整体叶盘的运动轨迹时，可将X、Y、Z 3个直线轴运动视为一个合成运动M1，其表达式不再限于直线描述形式，而允许以3次B样条曲线描述，拥有一个弧长参数s1，即：

式中：u为曲线参数，由s1决定；Nk,3(u)为3次 B样条曲线的基函数；)T为第k个控制点的坐标。

而 A、B、C 3 个旋转轴运动 M4、M5和 M6仍以直线形式进行描述，分别拥有各自的弧长参数s4、s5和s6，即：

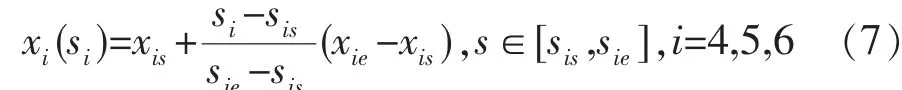
式（7）实际上就是式（5）的弧长参数表示形式。事实上，由于每个旋转轴运动只包含一个旋转轴，故每个旋转轴运动从起点到终点的弧长(sie-sis)就是起点和终点坐标之差的绝对值。直线轴合成运动与3个旋转轴运动（共4个运动）的4个弧长参数(s1,s4,s5,s6)代表了4个运动的插补进度，通过等比例的线性关系相对应（图4a）：

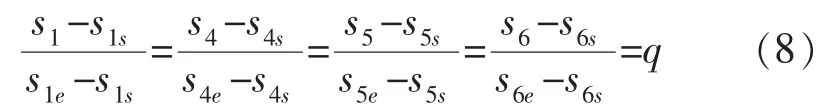
式中：q相当于当前插补进度占总插补长度的百分比。例如：在曲线段起点处，q=0，4个运动的弧长参数(s1,s4,s5,s6)=(s1s,s4s,s5s,s6s)，即起点处的弧长参数值；在曲线段终点处，q=100%，(s1,s4,s5,s6)=(s1e,s4e,s5e,s6e)，即终点处的弧长参数值；插补到曲线段中点时，q=50%，4个弧长参数正好分别处于起点弧长参数和终点弧长参数的中间值：

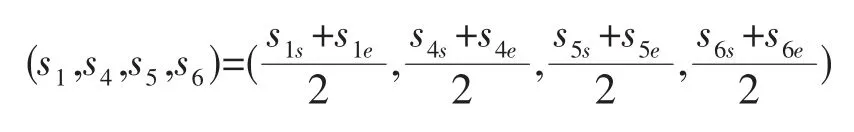
以式（6）作为直线轴合成运动M1的表达式，以式（7）作为旋转轴运动 M4、M5和 M6的表达式，以式（8）作为联系4个运动的纽带，这3个式子联合描述了一段多轴联动轨迹。

通过式（8）确立了分别属于4个运动的6个轴的同步关系后，剩下的问题就是确定每步插补时各个运动的弧长参数的增量。如1.1节所述，为了实现对曲线的直接精插补，就需满足“每步进给的曲线段在每个轴上的投影都≤1 BLU”的要求，单位弧长增量法取定每步插补的弧长增量值为Δs=1 BLU。而4个运动拥有4个弧长参数，每步插补时的每个弧长参数增量Δsi可能不一样，因此，为满足上述要求，就要使每步弧长参数增量最大的那个运动Mimax的Δsimax=1 BLU，其他3个运动的弧长参数增量自然就不会大于1 BLU（图4b）。各个运动的弧长增量计算方法用数学语言描述，即：

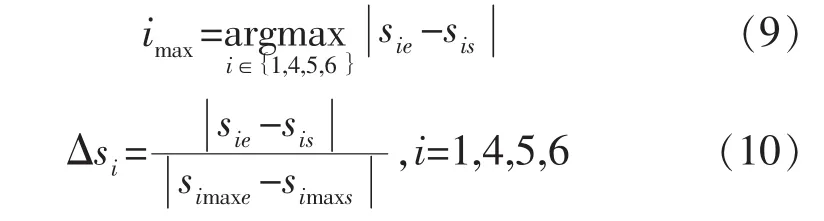
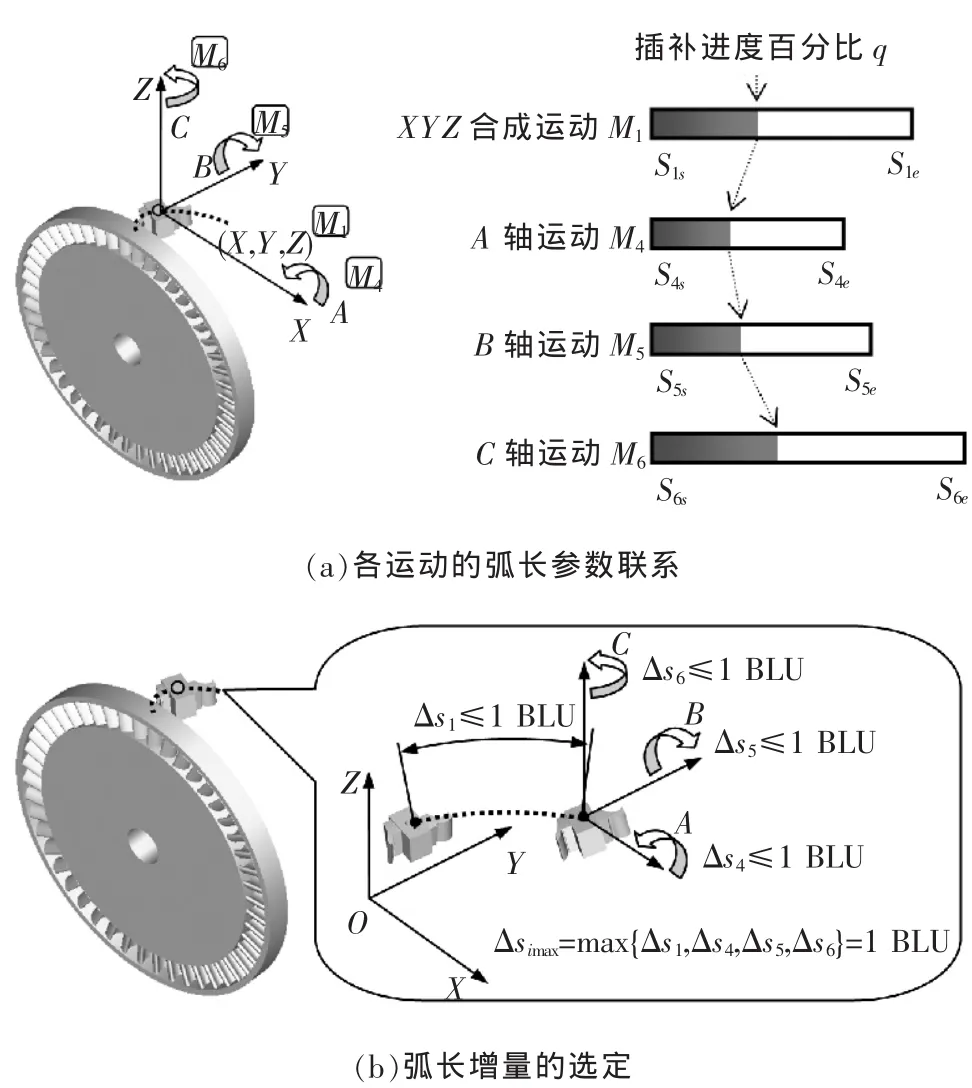
图4 直线轴与旋转轴的同步

注意到这时直线轴合成运动M1的弧长增量Δs1未必等于1 BLU，因此，在每步插补中，按1.1节所述的方法，先用二阶泰勒展开法计算直线轴合成运动曲线的参数：

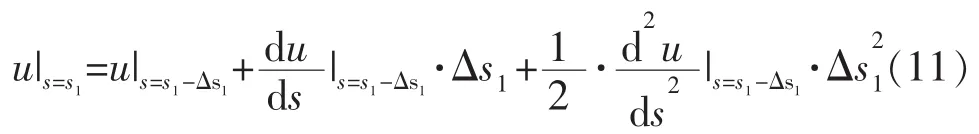
再代入式（6）求出X、Y、Z轴的插补点坐标。

将上述插补原理进行总结，可得到如图5所示的流程图。由于使用单位弧长增量法进行多轴联动插补时的弧长增量不是一般曲线意义下的弧长增量，而是将单位弧长增量法进行推广到直线轴和旋转轴联动的情形下选取出来的弧长增量。因此，将本插补方法称为“广义单位弧长增量法”。

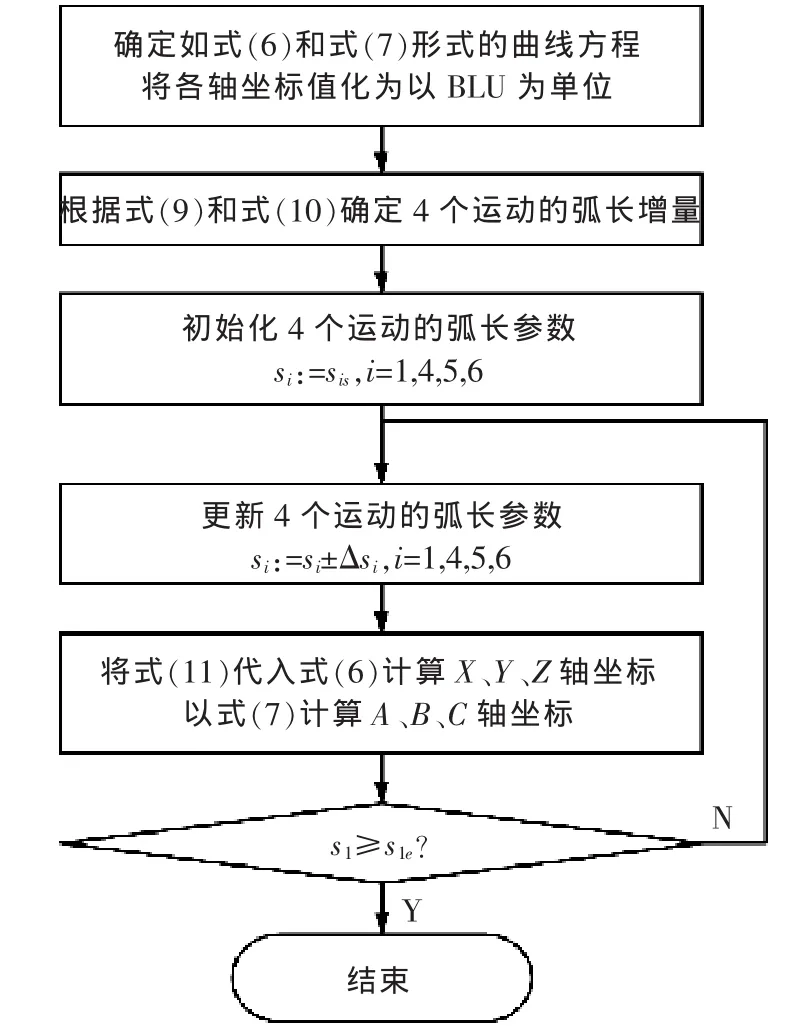
图5 广义单位弧长增量法插补一段多轴联动参数曲线轨迹的流程图

2 仿真与加工实验验证

2.1 闭式整体叶盘加工轨迹插补仿真

为了验证广义单位弧长增量法比传统数据采样法具有更高的精度和更少的存储空间消耗量，分别采用两种方法对闭式整体叶盘加工的一段参数曲线轨迹进行了插补仿真实验。直线轴合成运动M1以3次B样条曲线描述，其节点向量为：

{0.000 000 0，0.000 000 0，0.000 000 0，

0.000 000 0，0.015 289 8，0.041 548 9，

0.059 151 5，0.077 535 2，0.096 709 1，

0.116 667 6，0.137 415 7，0.144 276 6，

0.165 805 5，0.188 120 7，0.195 127 7，

0.218 193 9，0.242 769 3，0.249 331 0，

0.257 049 7，0.282 379 1，0.307 176 5，

0.331 428 5，0.335 833 0，0.358 138 5，

0.380 894 0，0.399 672 4，0.417 860 4，

0.434 732 8，0.451 001 4，0.459 105 1，

0.472 625 7，0.480 582 4，0.491 384 9，

0.501 215 9，0.510 697 6，0.521 109 8，

0.529 286 6，0.536 214 9，0.542 549 8，

0.548 316 7，0.553 534 2，0.557 568 2，

0.568 988 6，0.576 956 2，0.580 765 6，

0.584 556 7，0.587 897 7，0.591 361 6，

0.594 619 0，0.597 834 8，0.601 850 7，

0.610 777 0，0.618 991 7，0.627 191 3，

0.631 082 6，0.634 253 4，0.638 059 8，

0.641 822 7，0.646 040 3，0.650 222 1，

0.654 365 0，0.658 472 5，0.663 100 3，

0.674 476 1，0.679 812 0，0.691 842 3，

0.696 585 6，0.701 049 9，0.707 378 6，

0.714 357 5，0.720 639 7，0.728 265 7，

0.735 186 2，0.742 081 3，0.749 643 4，

0.757 189 0，0.764 030 8，0.771 537 1，

0.779 022 5，0.787 187 5，0.793 950 5，

0.802 076 8，0.809 484 2，0.817 568 9，

0.820 364 2，0.834 123 1，0.837 226 1，

0.844 516 4，0.847 262 0，0.855 880 8，

0.865 187 9，0.873 067 6，0.881 626 5，

0.890 165 5，0.898 683 0，0.907 174 2，

0.915 644 1，0.919 529 2，0.933 670 2，

0.937 526 2，0.940 857 5，0.950 570 3，

0.958 846 5，0.961 563 2，0.967 112 8，

0.974 059 1，0.977 404 2，0.980 371 1，

0.988 915 6，1.000 000 0，1.000 000 0，

1.000 000 0，1.000 000 0}

3个旋转轴运动则以直线形式进行描述。为了简化说明，取该多轴联动轨迹中的一段进行仿真实验比较，曲线数据见表1。

X、Y、Z、A、B 轴的分辨率均为 1000 BLU/°，C 轴的分辨率为2777.78 BLU/°。传统的数据采样法对直线轴合成运动M1执行离线粗插补，设其采样间隔弧长为10 BLU。广义单位弧长增量法的4个运动的弧长增量 Δs1、Δs4、Δs5和 Δs6的计算过程如下：

（1）求该段曲线内4个运动的弧长

（2）由式（9）可知 imax=6°

（3）由式（10）可求得各运动的每步弧长增量

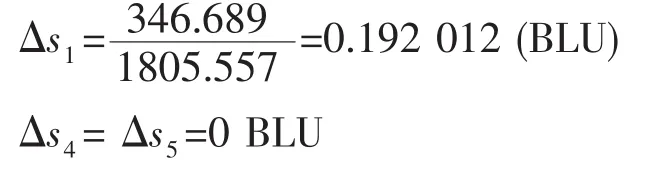
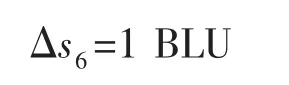
可见，C轴运动M6的弧长最长，故M6每步的弧长增量为1 BLU；其余3个运动的弧长增量都不大于1 BLU。

表1 仿真轨迹数据

两种插补法对所给曲线段的插补结果见表2。其中，弓高误差来自于直线轴合成运动的参数曲线插补，其定义和计算方法来自文献[19]。传统数据采样法粗插补生成了36个采样点，6个轴共需216个变量来存储采样点；广义单位弧长增量法存储数据个数为节点向量中的数据个数（113）、控制点数据个数（3×4=12）、弧长参数个数（2）和旋转轴端点个数（6）之和。注意到以广义单位弧长增量法插补所给曲线段实际上只需用到节点向量中的一部分节点值，因此，实际上要存储的数据个数可小于133。由表2可见，与传统数据采样法相比，广义单位弧长增量法以较小的存储空间实现了更高的插补精度，使弓高误差远小于1 BLU，在插补误差中只占极小的一部分，主要的插补误差由机床各轴的BLU长度决定，因而插补精度能控制在与机床分辨率相近的范围内。

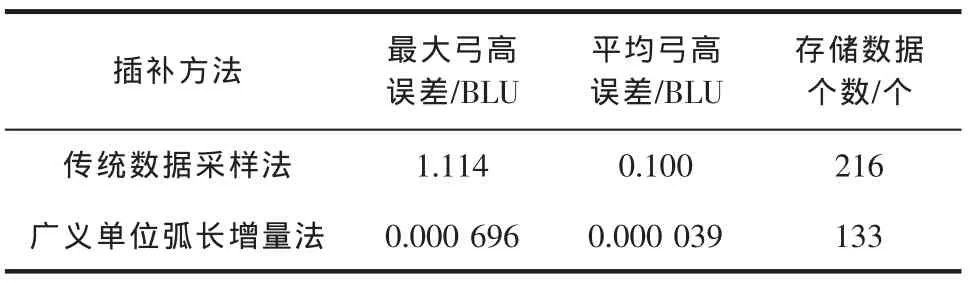
表2 一段多轴联动轨迹的插补仿真结果

2.2 闭式整体叶盘加工实验

为验证广义单位弧长增量法的稳定性和可靠性，在HE70型六轴联动电火花加工机床的数控系统上实现了广义单位弧长增量法，并进行了闭式整体叶盘加工试验。图6是加工样件。加工过程稳定，直线轴和旋转轴均按所给指令执行同步进给运动，所有需要反向插补的抬刀、短路回退和暂停/退刀功能在执行过程中均能准确地沿原轨迹回退和前进，工具电极与工件之间无干涉现象出现，证明广义单位弧长增量法适用于多轴联动电火花成形加工的场合。

图6 闭式整体叶盘加工样件

3 结语

本文从电火花加工数控系统插补器中常用的脉冲增量法出发，将单位弧长增量法推广到多轴联动电火花加工的应用中，形成了具有直线轴运动与旋转轴运动同步功能的广义单位弧长增量法。其中，直线轴的合成运动允许以一般的参数曲线形式进行描述，每个旋转轴运动分别以直线形式描述，各运动之间以弧长参数为纽带，按弧长比例决定每个运动的插补进度，并取定弧长最长的运动的每步弧长增量为1 BLU，使插补误差控制在与机床分辨率相近的范围内。由于该方法属于能直接生成各轴进给脉冲的精插补方法，因此，不论是采用伺服电机还是步进电机的机床均可应用。

对闭式整体叶盘加工轨迹的插补仿真表明，广义单位弧长增量法与传统的数据采样法相比，具有较低的存储空间消耗和较高的插补精度。通过闭式整体叶盘加工实验验证了广义单位弧长增量法的稳定性和可靠性。

[1] Shpitalni M，Koren Y，Lo C C.Realtime curve interpolators[J].Computer-Aided Design，1994，26（11）：832-838.

[2] Fleisig R V，Spence A D.A constant feed and reduced angular acceleration interpolation algorithm for multi-axis machining[J].Computer-Aided Design，2001，33（1）：1-1 5.

[3] Heng M，Erkorkmaz K.Design of a NURBS interpolator with minimalfeed fluctuation and continuous feed modulation capability[J].International Journal of Machine Tools and Manufacture，2010，50（3）：281-293.

[4] Yeh S S，Hsu P L.Adaptive-feedrate interpolation for parametric curves with a confined chord error[J].Computer-Aided Design，2002，34（3）：229-237.

[5] 刘萍，王民权，范进桢，等.FANUC系统中实时前瞻的NURBS插补研究与实现[J].机械科学与技术，2012（5）：791-795.

[6] 李佳特.FANUC最新数控和伺服技术[J].机械工人（冷加工），2007（2）：20-22.

[7] 谭天.西门子公司在IMTS2000上的新产品 [J].世界制造技术与装备市场，2002（1）：60.

[8] Suh S H.Theory and design of CNC systems[M].New York：Springer，2008.

[9] 杨大勇，付伟，任连生，等.五轴联动精密电火花加工复杂轨迹控制技术研究[C]//第13届全国特种加工学术会议论文集[M].哈尔滨：哈尔滨工业大学出版社，2009：63-69.

[10]黄海鹏.多轴联动电火花加工数控系统软件构建及其应用研究[D].哈尔滨：哈尔滨工业大学，2010.

[11]李志勇.基于Linux多轴联动电火花加工数控系统及相关技术研究[D].哈尔滨：哈尔滨工业大学，2004.

[12]刘丽丽.五轴微细电火花加工数控系统关键技术研究[D].哈尔滨：哈尔滨工业大学，2013.

[13]Chang Y F，Hong R C.Parametric curve machining of a CNC milling EDM[J].International Journal of Machine Tools and Manufacture，2005，45（7）：941-948.

[14]魏力.微细电火花铣削加工插补技术与轨迹规划研究[D].大连：大连理工大学，2012.

[15]Liang Su，Zhao Wansheng，Xi Xuesheng.Design of a real-time NURBS interpolator with constant segment length for milling EDM [J].International Journal of Advanced Manufacturing Technology，2013，67 （1-4）：427-440.

[16]陈默，陈昊，赵万生.电火花线切割机床四轴联动单位弧长增量插补法[C]//第15届全国特种加工学术会议论文集（上）.南京，2013：259-265.

[17]Piegl L，Tiller W.The NURBS book[M].2nd edn.New York：Springer，1997.

[18]Cheng M Y，Tsai M C，Kuo J C.Real-time NURBS command generators forCNC servo controllers[J].International Journal of Machine Tools and Manufacture，2002，42（7）：801-813.

[19]赵世田，赵东标，付莹莹.自由曲面加工刀具路径生成高精度变步长算法研究[J].机械科学与技术，2010（1）：32-35.