单脉冲放电移动放电点温度场研究

彭威震，郭常宁，雍耀维

（上海交通大学机械与动力工程学院，上海200240）

作为最常用的非传统加工方式之一，电火花加工以其非接触、宏观力小等特点，在热处理材料、微细加工、陶瓷材料加工和现代复合材料加工等领域得到广泛应用。然而，电火花加工理论研究的滞后在很大程度上阻碍了电火花加工技术应用的进一步发展。关于材料的去除机理，现在一般认为在脉冲放电时间较长时，熔化、气化是材料去除的主要形式。针对放电通道中等离子体的扩张及引起的温度场变化，很多学者做了深入研究。热源也由原来的简化热源到考虑通道扩张，以各种经验公式为等效输入的热源半径，随半径变化而引起的热流密度的变化、相变，且考虑到材料在不同温度下不同的热物性[1]。

在一次连续脉冲的放电中，各个时刻放电点的中心位置是不断变化的。Kunieda等[2]通过实验观测到单脉冲放电过程中放电点的移动，亓利伟[3]和楼乐明[4]利用放电通道波动性的观点解释了该现象，并提出了放电通道位形的概念。现有的材料去除模型均假设放电点中心不移动，没有考虑放电通道震荡使放电点中心移动引起热源在空间分布上的变化，进而对温度场分布产生影响。为此，本文在建立单脉冲放电热源时考虑了放电点中心移动，利用有限元软件进行了数值模拟，并选定了几组电流和脉宽进行了单脉冲放电实验，验证本文所提模型的有效性。

1 放电通道的扩张与放电点移动

在放电过程中，放电通道是由数目大致相等的电子和正离子组成，对外呈电中性。等离子体中间密度高，边缘密度低，整体呈现出高斯分布。将等离子体看成热源，经推导得到的热源表达式为[5]：

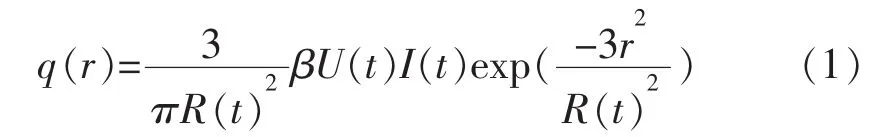
式中：U（t）为放电时的维持电压，V；I（t）为加工平均电流，A；一般来说，电压和电流值是震荡的，但变化不大，可当成定值；β为能量分配系数；R（t）为通道半径。

夏恒[6]以油为工作液、工件和工具电极均为铜进行了试验和理论分析，认为分配到阴极的能量占总能量的25%，分配到阳极的能量占40%，其余的35%能量损失在放电通道中，且能量分配系数与放电脉冲宽度无关。结合实验，本文取分配到阳极的能量占总能量的40%。

从放电开始到一定时间内，通道半径由小到大扩张。放电通道的等效热量输入半径经验公式为：

式中：Rp（t）为通道中等离子体半径，μm；Ip为加工平均电流，A，计算时代替I（t）；ton为放电脉冲宽度，μs。

等离子体易受到干扰而产生振荡，中心点位置不会固定于一点，而会在一定区域内移动。经优化得到放电通道的位形半径公式为[4]：

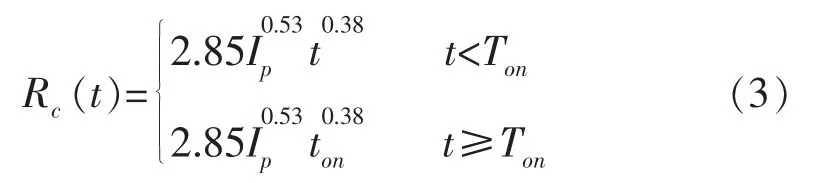
式中：Rc（t）为放电通道形位半径，μm；Ip为加工电流，A；Ton是最佳脉宽，μs。最佳脉宽对应的形位半径为最优半径，可由式（4）得到[5]：

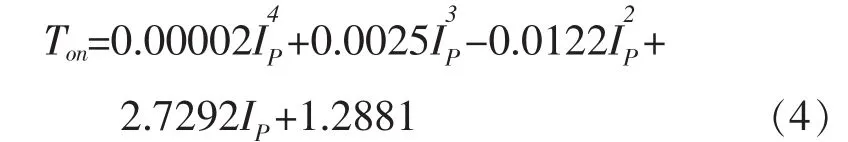
进行热源加载时，需在时间上离散化处理，即将热源分为有限步进行加载。在每个载荷步下，热流密度不变，而通道半径随着加载步骤的增加而增大。在放电过程的某一时刻，放电通道的热源半径与位形半径是两个重要概念，形位半径所得到的圆（形位圆）包括等效热源半径所得到的圆（热源圆）。在放电的某一时刻，热源以等效热量输入半径得到的高斯热源作为加载热源，在下次加载时，放电中心点可能不在同一位置，但加载区域会被限制在该时刻的形位圆内。在整个放电过程中，放电形位半径的中心点不变，大小由式（3）决定；而等效热量输入半径的大小由式（2）决定，热源中心点的位置由该时刻的形位圆和热源圆共同决定。在放电通道的形位半径没有达到最优半径之前，形位半径和等效输入半径都按式（3）和式（2）扩张。当达到最优半径后，为简便起见，形位半径和等效输入半径均停止扩张，其位置关系见图1。

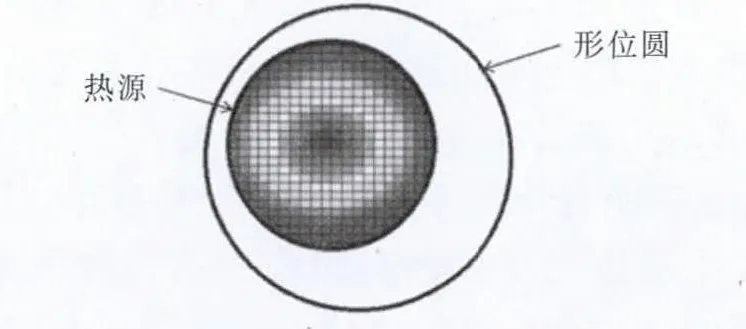
图1 形位圆与热源位置关系

2 工件温度场模型的建立

电火花加工过程中，工件和电极受到放电通道中高温等离子体的作用而产生熔化、气化，将与电极接触的等离子体看成热源。工件和电极的内部升温是由热传导引起的。考虑到材料在不同温度下具有不同的热学物理参数，由傅里叶定律可得三维热传导方程：

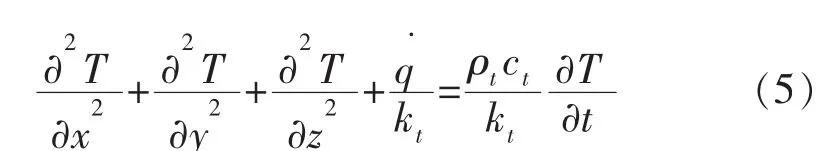
式中：kt、ρt、ct分别为材料的热传导率、 密度和比热容。

本文采用有限元软件ANSYS进行数值仿真，首先需确定整个几何模型的尺寸。由于放电时间较短，受热区域较小，离放电区域较远的地方温度梯度较小，结合实验所用的电流及放电脉宽，几何模型的尺寸为 600 μm×600 μm×300 μm。 分析时，单元类型选择为SOLID70，这是一个在三维瞬态热分析经常用到的单元，由于热源加载表面的载荷为热流，而非加载区域要和周围介质产生对流，因此还需一个表面效应单元SURF152。在热源加载表面，将随时间和位置变化的热源加载在表面效应单元SURF152上，而SOLID70上加载对流载荷。网格的大小直接影响着计算时间和计算精度。综合以上分析结合实际仿真得到的结果，在放电区域实现均匀网格划分，网格的大小为 1 μm×1 μm，而远离放电区域实行非均匀等比划分。网格模型见图2。

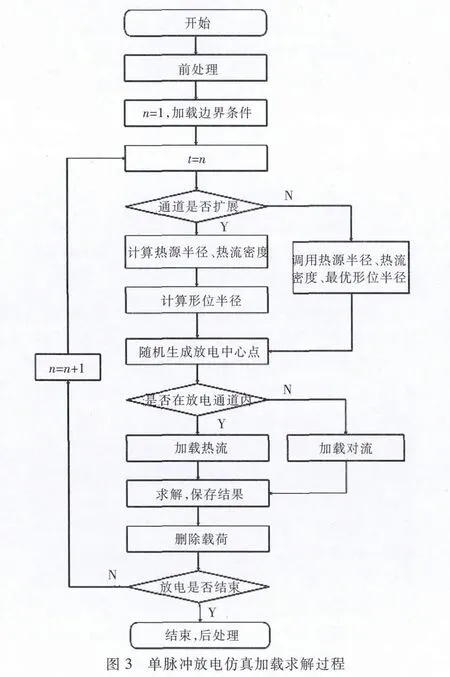
由于热源较复杂，加载位置随时间不断变化，整个ANSYS模型的前处理和热源加载均用ANSYS参数化设计语言编写。放电点位置的随机性是通过ANSYS内部的随机函数实现的，热流加载方法及过程如下：在放电的某一时刻，首先判断通道是否扩张，计算在该时刻放电通道的形位半径和等效热源半径；然后生成2个随机数，分别表示极坐标下放电中心点在全局坐标系下的极半径和角度，且必须保证放电通道的形位圆对热源圆的包含关系；接着，以放电点为中心建立局部坐标系，实现高斯热源的加载和其他区域热对流的加载；最后，实现求解并删除热流。整个加载与求解过程见图3。

为验证模型的有效性，将仿真得到的结果与单脉冲放电实验结果进行对比。实验在ROBOFORM 35机床上进行。选取3组电流参数（表1），加工电流与最佳脉宽的关系由式（4）得出，每组电流下选取4组脉冲宽度进行加工，通过对比实验结果和仿真结果，给出相应的解释和讨论。实验用电极材料为紫铜，工件材料为高速钢M2，工作液为煤油，加工极性为正极性加工，其他加工条件见表2。

表1 不同加工电流下的最佳脉宽

表2 实验条件

3 仿真及实验结果

图4a是加工电流为4 A、脉冲宽度为50 μs时热源最后一步加载完成后，工件热流加载区域表面的温度场分布。图4b是单脉冲放电实验得到的放电坑。从图4c可看出，放电结束后，中心位置温度高，但由于放电过程中等离子体的中心点不固定，温度最高点并不在几何模型的中心处，而等温线也不是绝对的圆形。

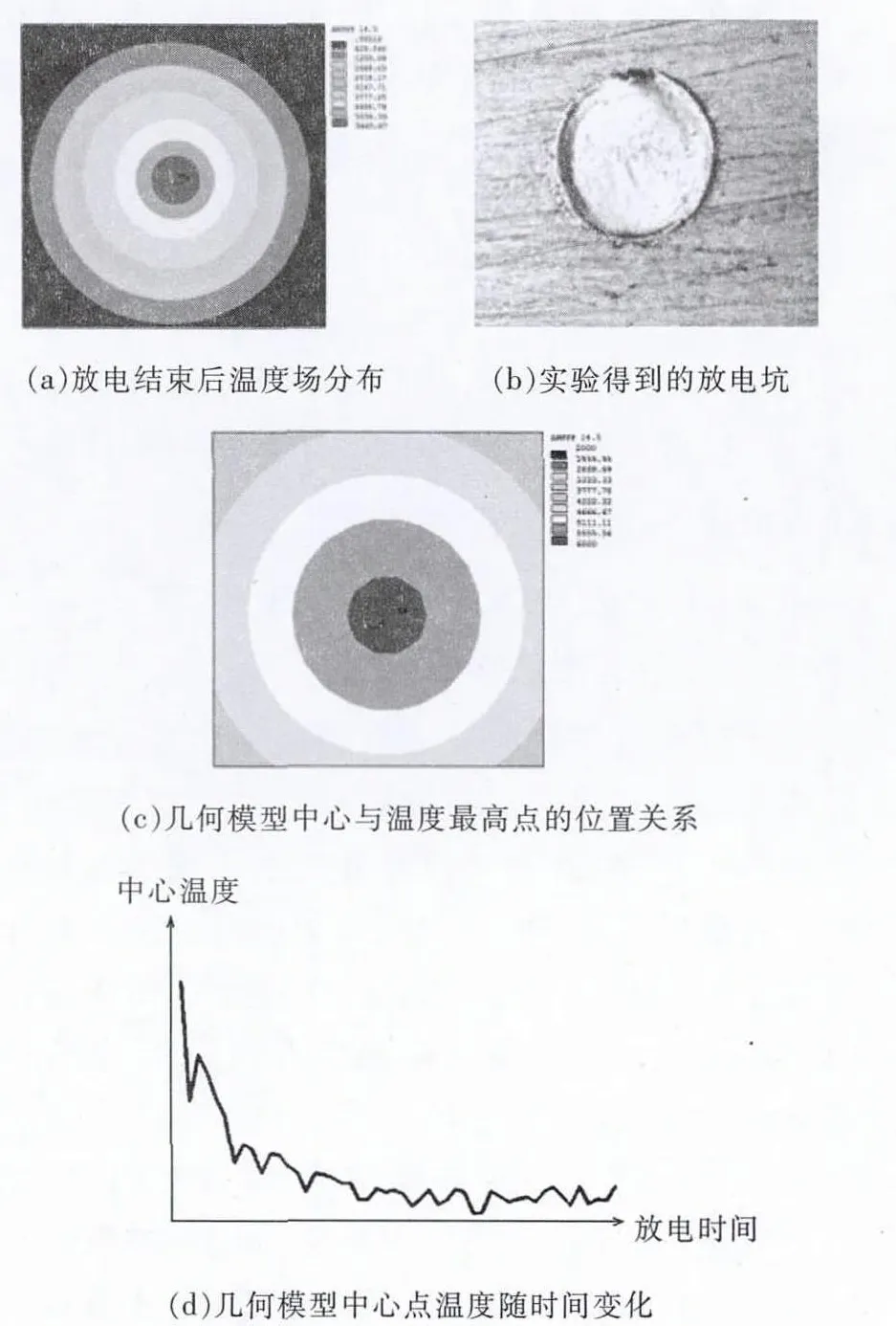
图4 仿真与实验结果

图4 d是几何模型（形位圆）中心的节点温度随时间的变化曲线。可看出，放电刚开始时，放电通道的等离子体半径小，热流密度大，材料的气化是材料去除的主要形式，这符合短脉冲加工时的材料去除规律；随着放电的继续，中心处的温度降低，且由于放电点的移动，中心温度会有一定的波动，此时，熔化是材料去除的主要形式。

从图5可看出，在加工电流相同的条件下，随着脉冲宽度的增加，无论实际测量得到的放电坑半径值还是仿真得到的放电坑半径值均增大。这是因为当加工电流不变时，随着脉冲宽度的增加，传递到工件和工具电极上的能量也越多，将有更多的材料受热熔化、气化，因而放电坑的半径会增大。但随着放电时间成倍增加，放电坑半径却没有相应成倍增加，如在加工电流为4 A时，脉冲宽度为100 μs是脉冲宽度为12.8 μs的将近8倍。但无论仿真还是实验得到的数值，前者放电坑的半径均不到后者的2倍。这是因为随着脉冲宽度的增加，放电通道中热源半径更大，会有更多的能量以热传导的形式散失出去，而不能有效地去除材料。

图5 不同脉宽下的放电坑半径实验值与仿真值比较

将仿真得到的放电坑半径与实验得到的放电坑半径之比定义为模型的精度。由图6可看出，在选定的电流和脉宽参数下，模型在大部分情况下拥有70%以上的精度，最差的情况下也有65%的精度。导致模型出现误差的原因有以下几点：第一，计算模型所得半径时只考虑了最后一步时超过熔点部分的区域，但由于放电点的跳动，导致模型在一些节点上温度并不一直升高，这就导致在中间某一段时间超过了熔点的区域由于远离了放电点在最后一步时，最终单元显示温度却在熔点以下，因而带来了误差；第二，模型在热源加载过程中并未考虑材料的去除，这就导致很多超过熔化甚至气化温度的材料还在吸收热量，而实际上这部分热量应该传递到内部；第三，建立模型的简化所带来的误差，如材料的热物性在较高的温度很难准确获得，放电点移动的模式等。

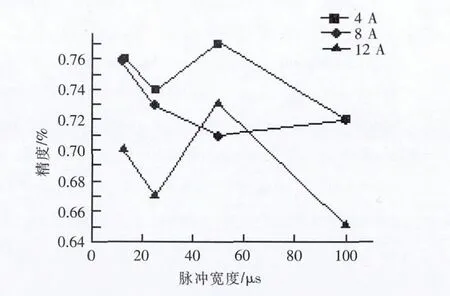
图6 不同加工电流和脉冲宽度下模型的精度

图7 是脉冲宽度为12.8 μs时，不同加工电流下的放电坑半径实验值与仿真值比较。可看出，在相同的脉冲宽度下，随着加工电流的增大，无论仿真还是实验结果，放电坑的半径均增大。这是因为在脉宽不变的情况下，随着加工电流的增加，有更多的能量用来去除材料。

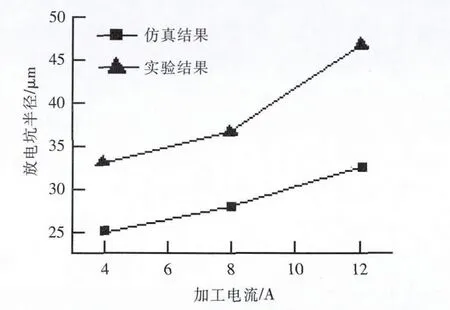
图7 脉冲宽度为12.8μs下，不同加工电流的放电坑半径实验值与仿真值比较

4 结论

（1）通过将放电通道中等离子体产生的高斯热源限定在形位圆内，建立了移动放电中心点材料去除热学模型。模型显示，放电结束后温度的最高点并不在几何模型表面的中心；几何模型表面中心温度在放电刚开始时较高，之后下降，由于放电中心点的移动，温度会出现波动。

（2）利用现有的电火花加工机床进行了单脉冲实验，并比较了不同电流和脉冲宽度下放电坑半径的实验值和仿真值。结果表明，模型具有70%左右的预测精度。

[1] 解宝成.微小孔及阵列孔微细电火花加工的若干基础问题研究[D].哈尔滨：哈尔滨工业大学，2013.

[2] Kunieda M，Xia H，Nishiwaki N.Observation of arc column movement during monopulse discharge in EDM[J].CIRP Annals-Manufacturing Technology，1992，41 （1）：227-230.

[3] 亓利伟，楼乐明，李明辉.放电通道的波动性与电火花加工机理 [J].上海交通大学学报，2001，35 （7）：989-992，997.

[4] 楼乐明.电火花加工计算机仿真研究[D].上海：上海交通大学，2000.

[5] 崔景芝.微细电火花加工的基本规律及其仿真研究[D].哈尔滨：哈尔滨工业大学，2007.

[6] Xia H，Kunieda M，NishiwakiN.Removalamount difference between anode and cathode in EDM process[J].International Journal of Electrical Machining，1996，1：45-52.