基于实例分析的单因素方差探究

□陈 悦 魏巍巍

方差分析在实际应用中出现于20 世纪20年代，由英国统计学家R．A．Fisher 提出并予以应用。方差分析主要是应用于自变量对因变量的影响。在检验多个总体的均值是否相等时，借助方差分析，对数据的误差来源进行检查，从而判断一个或多个因素对总体均值的影响。由此，方差分析根据因素的多少分为单因素方差分析和多因素方差分析。传统方差分析的应用受诸多因素的限制，尤其是其计算量对普及应用方差分析的影响。但随着现代计算机技术的不断发展，方差分析更多地被应用于生活领域，如经济、生物医药、社会学等多个方面。为此，本文借助实例分析的方法，探索单因素方差分析在实际应用中存在的优点和缺点。

一、单因素方差分析的工作原理

方差分析在实际应用中是在一定情况下的统计假设试验。方差分析的对象是试验所得数据，目的是对客观规律的发现和揭示。单因素方差分析涉及到因素、水平以及单因素试验三个层次，所谓因素是指对研究对象具有影响的某一指标、变量;所谓的水平是指影响因素在不同状态和变化下的划分等级或组别;所谓单因素试验是指每次试验只考虑一个因素的试验。以下将举例说明单因素方差分析的工作原理，以便于更好地理解和认识单因素方差分析。

例如以不同种类的抗生素同血浆蛋白质结合状况，分析抗生素与血浆蛋白质结合的百分比，为使用药量和测定药效提供参考。如表1，实验数据所示，五种不同的抗生素在注入羊的体内后，测定的抗生素与血浆蛋白质结合的百分比。假设各总体服从正态分布，并且各总体方差相同，其中α=0．05代表显著性水平，百分比检查均值并无显著性差异。本次试验先根据实际情况提出原假设H0 与备择假设H1，然后寻找适当的检验统计量进行假设检验。以抗生素为单一因素，以血浆蛋白质与抗生素的结合百分比为实验指标，以5种不同抗生素代表单一因素的5 种不同水平。其余一切在本实验中都被视为条件相同。以此检查血浆蛋白质与抗生素结合百分比均值差异性，探索单一因素抗生素对二者结合百分比的显著性影响。

表1 五种不同抗生素与血浆蛋白质结合的百分比(%)

(一)检验假设。假设，因素A(即抗生素)有s(=5)个水平A1，A2…A5，在每一个水平Aj(j =1，2，…，s)下进行了= 4次独立试验，得到如表1 所示的结果。所有实验结果都是一个随机变量。表1 中的数据可以视作来自s 个不同总体的样本值，其中每个水平对应一个总体，形成一一对应的关系。将各个总体的均值依次记为μμμ，则依据题意进行检验假设。

Η0:μ1=μ2…μs。

Η0:μ1，μ2，…μs不全相等。

为了便于讨论单一因素方差分析过程，现在引入总平均μ，得出下列公式:

在引入总平均μ 的基础上，再引入水平的效应，得出下列公式:

依据假设则有n1δ1+n2δ2+…n8δ8=0，表示水平下的总体平均值与总平均的差异。

在以上检验假设的基础上，本案例的假设:

H0:δ1=δ2…=δ8=0。

H1:δ1，δ2，…，δ8不全为零。

因此，单因素方差分析的目标就是检验s 个总体的均值是否相等，也即是检验各水平的效应是否都等于零。

(二)检验所需的统计量。如果所有体均服从正态分布，而且所有方差相等，也即是假定各个水平Ajj…s 下的样本xjxjxnjj 来自正态总体N(，)，和未知，且设不同水平下的样本之间相互独立，由此可以通过从总平方和的分解中得到单因素方差分析所需的检验统计量。接下来先引入样本各种水平下的样本平均值、数据总平均值以及总平方和公式:

水平下的样本平均值:

数据的总平均:

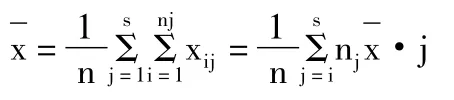
总平方和:

总变差ST 和总平方能够反映全部试验数据之间的差异，因此将总变差ST 分解，其中:

综上所述各项(xij－x·j)2代表在水平下，由随机误差所引起的样本观察值与样本均值的差异，因此，称为误差平方和。由水平以及随机误差所引起的样本平均值与数据总平均的差异，因此，称为因素A 的效应平方和。由上述可以证明与相互独立，且当H0=δ1=δ2=…=δs=0 为真时，与分别服从自由度为s －1，n－ s 的分布，即

由此，当H0:δ1=δ2=…δs=0 为真时F(s －1，n －s)则为单因素方差分析所需的服从F 分布的检验统计量。

二、单因素方差分析应用实例

对于上述实例，假定给定显著性水平α=0．05，我们可以求出5 个因素的样本均值分别为=26．8，=28．3，=22．5，=31．1，=24．8。由此可见因素的四个总体均值的确存在差异。

借助Excel 中单因素方差分析工具，对上述实例进行分析，可以得到表2 的分析结果。

表2 方差分析——单因素方差分析

通过分析我们发现，F =12．0172 ＞=1．6082，由此可见，在显著性水平α=0．05 时，可以相信5 种不同抗生素与血浆蛋白质结合百分比存在显著性差异。

三、结语

方差分析能够较好地应用于统计推断之中，也即是根据部分资料，对全部研究对象进行科学的统计推断，以得到有价值的结论。目前，随着计算机技术的不断发展，借助计算机技术解决了方差分析计算量大的问题，从而提高了方差分析在生活各领域的应用，如生物领域、医药领域、经济领域等等。尤其是单因素方差分析，在分析单因素对多组群实验数据进行方差分析过程中，呈现出诸多优势，而被社会各领域广泛应用。

单因素方差分析方法作为方差分析方法的一种，随着计算机技术的不断发展，在对比分析观测变量总的误差平方和各部分所占比例方面具有显著的优势，对于研究自然变量与因变量之间的关系，具有重要的意义。因变量的变动与自变量之间具有密切的联系，借助单因素方差分析，若在总的误差平方和中，组间误差平方和所占比例过大，则说明自变量引起因变量的改变。可以从自变量的角度揭示因变量的变动原因。反之，则不能够从自变量的角度解析因变量的变动，也即是自变量的不同水平对于因变量的影响不显著。其变动由随机变量因素决定。

单因素方差分析法的一个突出优势是判定自变量是否为影响因变量变化的显著性影响因素。如果通过单因素方差分析确定自变量诱发因变量的变动，对因变量具有显著性影响，则可以说明实验中各总体均值间存在显著性差异。但这种显著性差异并不代表每两个总体均值间均存在显著性差异。换言之，单因素方差分析能够确定各总体间均值差异是否显著，对于哪两个总体间均值差异是否显著，并未有效证实。为此，在探析多个总体间均值差异中的每两个总体间均值是否显著差异，仍然需要进行总体间的两两均值比较。这也就是多重比较，即在多个总体均值之间进行两两总体均值的显著差异化比较。

［1］李玉毛．单因素方差分析在经济数据分析中的应用［J］．赤峰学院学报(自然科学版)，2012，28(2):18～19

［2］印德中．EXCEL 在方差分析中的应用［J］．中国现代教育装备，2011，17:23～25

［3］林伟初．概率论与数理统计［M］．上海:同济大学出版社，2009:153～159