改进型钢管混凝土柱单腹板肩梁有限元分析及设计方法
王宗让,苏明周,董振平
(1.陕西师范大学基建处,陕西 西安710061;2.西安建筑科技大学土木工程学院,陕西 西安 710055 )
钢管混凝土结构能有效利用钢材与混凝土材料的力学特性,承载力高且经济性好,被广泛应用于房屋建筑工程结构中.工业厂房结构也大量采用钢管混凝土斜腹杆双肢柱形式作为竖向承重构件,然而由于我国工业厂房应用钢管混凝土构件时间不长,且相关研究不够深入,从结构设计到施工仍存在一些不足.从实际使用过程中出现的问题来看,主要为肩梁等构造连接性能难以保证,钢管内混凝土浇注密实度不足,以及后期结构维护不当.
国内部分学者对钢管混凝土肩梁进行了一定研究.于安林、童根树教授[1-4]对钢管混凝土双肢柱单腹板肩梁节点进行了承载力试验研究和理论分析,提出了一种考虑翼缘部分有效的实用设计公式.通过对钢管混凝土四肢柱人字形缀杆以及单斜缀杆双腹板肩梁承载力的研究发现,人字形缀杆结构与单斜缀杆相比承载力大约提高20%,但人字形缀杆会对肩梁腹板产生较大反力,导致腹板过早发生屈曲.金天德、饶芝英[5]对钢管混凝土柱肩梁进行了只考虑弹性阶段的有限元分析,得出腹板与钢管采用嵌入形式可有效提高钢管承载力的结论.沈祖炎和郑沂[6]对钢管混凝土柱肩梁极限承载力和整体刚度计算进行了研究,提出了一种肩梁转动刚度的简化计算方法.本文在1:3模型试验的基础上,对改进型钢管混凝土柱单腹板肩梁进行了有限元参数分析,探讨了肩梁高厚比与高跨比对构件承载能力的影响,并给出了设计公式.为这种改进型肩梁在工程中应用打下了一定的基础.
1 工程背景及试验介绍
1.1 工程背景
宝钢在其冶金厂房中使用双肢单腹板肩梁结构,在使用过程中出现一定程度的破损情况,具体破坏形式见图1、表1和表2.针对上述情况,西安建筑科技大学结构安全研究所提出了一种单腹板肩梁的改进形式,并进行相关试验,对改进型肩梁的承载能力、受力性能及破坏形式进行研究,研究结果对肩梁结构的设计以及维修管理工作具有积极的意义.本文在此基础上,进行有限元参数分析,并根据分析结果,提出了设计建议.1.2 改进型单腹板肩梁试验概况

图1 肩梁具体破坏形式Fig.1 Damage forms of shoulder beam

表1 吊车梁与支座连接损伤情况[7]Tab.1 Damage of crane beam and support connection[7]
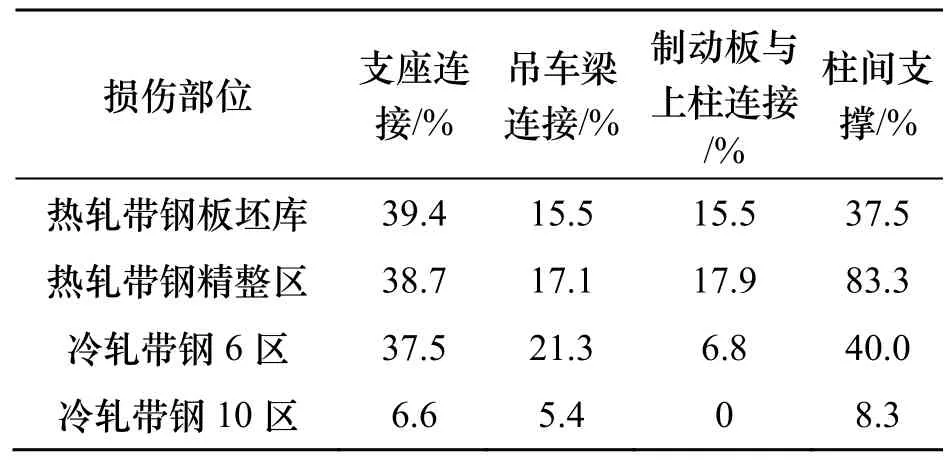
表2 吊车梁伤统计结果[7]Tab.2 Statistical results of crane beam damage [7]
试验试件根据《钢结构设计规范》(GB50017-2003)[8],《建筑抗震设计规范》(GB-50011-2001)[9]进行设计.设计了2个钢管混凝土中柱肩梁试件 (ZJ-1、ZJ-2),2个钢管混凝土边柱肩梁试件 (BJ-1,BJ-2),试件采用 1:3缩尺模型.模型具体形式、尺寸,试验加载方案及制度见文献[10].试件ZJ-1、ZJ-2破过程式为:当肩梁承载力接近屈服荷载时,腹板受压区域出现了屈曲,随着荷载增大,变形逐渐向斜下方发展,直至出现一条与水平线成大约45o的斜压带,引起翼缘屈曲,最终结构由于变形过大而丧失承载能力.具体破坏形式见图 2,荷载位移曲线见图 4.中柱肩梁在荷载作用下,柱受压翼缘基本未发生破坏,而肩梁腹板发生较大变形;随着荷载继续增大,塑性区继续扩展,最终,肩梁由于腹板变形过大而丧失承载力,中柱肩梁的破坏模式为腹板屈曲而引起截面破坏.
BJ-1,BJ-2的破坏过程与试件 ZJ-1、ZJ-2不同.表现为当肩梁承载力接近屈服荷载时,受压翼缘发生轻微屈曲变形;随着荷载增大,腹板受压区域出现了屈曲,形成了一条与水平线成约 45°的斜压带,最终结构由于变形过大而丧失承载能力.具体破坏形式见图 3,荷载位移曲线见图 5.边柱肩梁的破坏由受压翼缘开始,翼缘发生屈曲后,对腹板的约束减弱,进而腹板发生较大变形,整个截面发生屈服而丧失承载力,边柱肩梁的破坏模式为翼缘屈曲而引起的截面破坏.

图2 试件ZJ-1、ZJ-2破坏情况Fig.2 Damage forms of specimen ZJ-1 and ZJ-2

图3 试件BJ-1、BJ-2破坏情况Fig.3 Damage forms of specimen BJ-1 and BJ-2

图4 试件ZJ-1、ZJ-2荷载-位移曲线Fig.4 Load -displacement curve of specimen ZJ-1 and ZJ-2

图5 试件BJ-1、BJ-2荷载-位移曲线Fig.5 Load -displacement curve of specimen BJ-1 and BJ-2
2 有限元模型分析
采用有限元软件ANSYS进行建模分析,钢材与混凝土的本构关系根据试验试件的材性试验确定,钢材采用Solid45单元,混凝土采用Solid65单元.Q345钢的弹性模量E=1.92×105N/mm2,泊松比ν=0.3,屈服强度fy=414 N/mm2,极限抗拉强度fu=569 N/mm2.Q235钢的弹性模量 E=2.0×105N/mm2,泊松比 ν=0.3,屈服强度 fy=311 N/mm2,极限抗拉强度fu=472 N/mm2;混凝土标号为C30,不考虑包辛格效应影响.钢材与混凝土的本构模型见图 6,有限元模型见图 7.将有限元计算结果与试验结果进行比较,见图8和图9,荷载位移曲线对比见图10.经过对比可知计算结果与试验结果能够较好吻合.
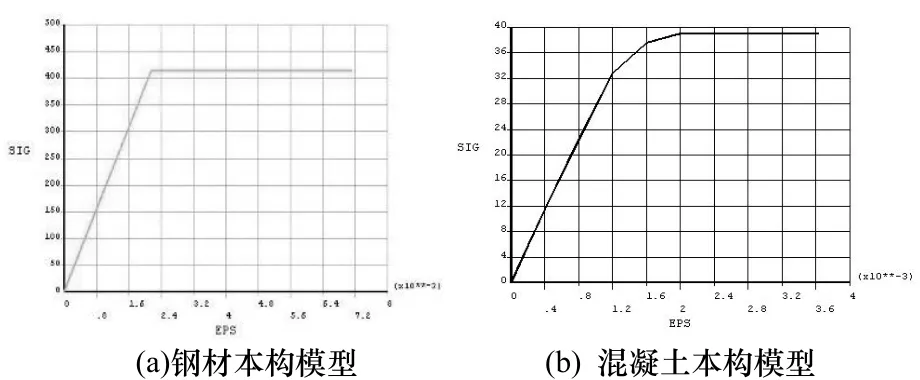
图6 材料本构模型Fig.6 Material constitutive model
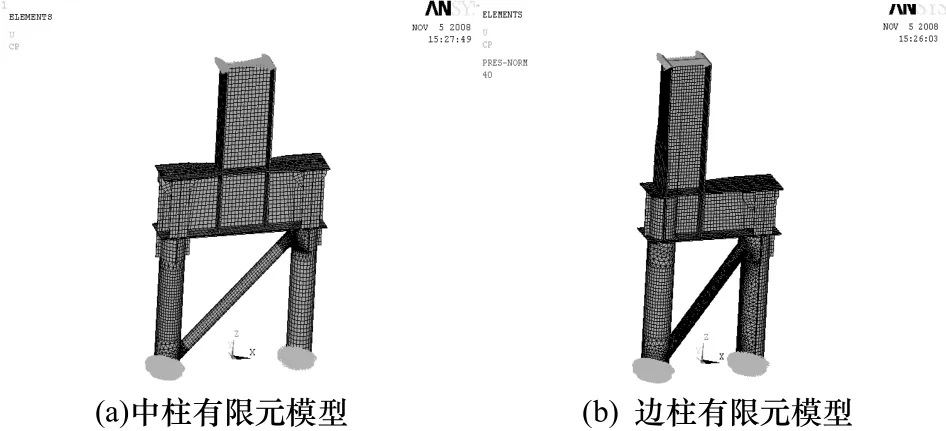
图7 有限元模型Fig.7 Finite element model
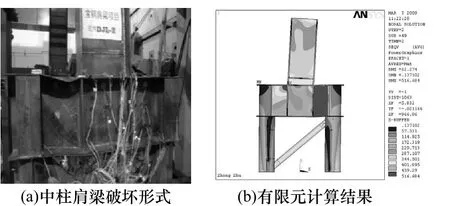
图8 中柱试件破坏形式比较Fig.8 Comparison of damage forms of middle column specimen
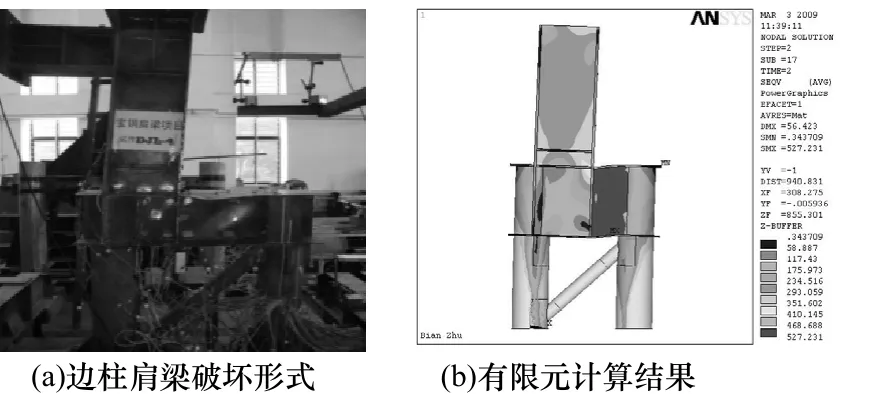
图9 边柱试件破坏形式比较Fig.9 Comparison of damage forms of side column specimen
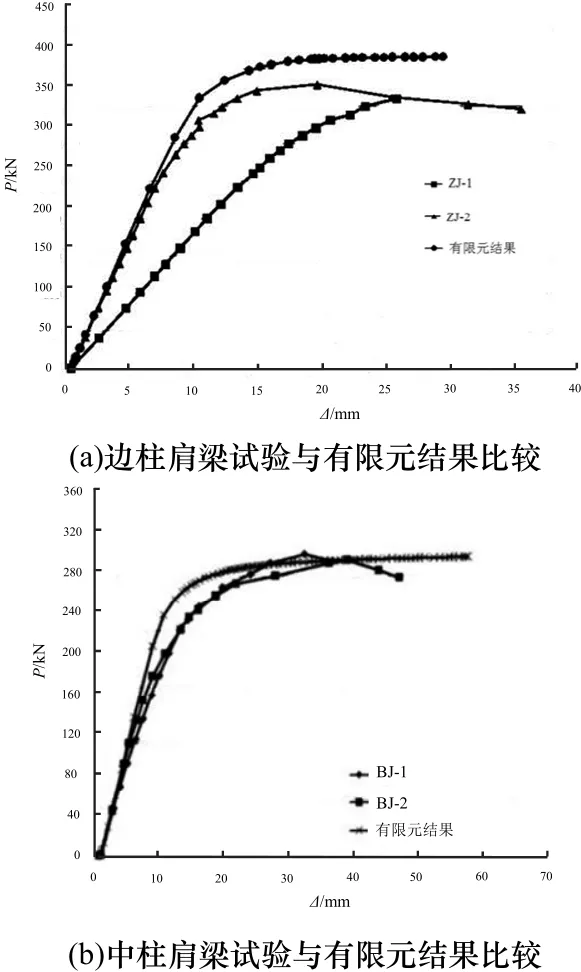
图10 试验与有限元荷载-位移曲线比较Fig.10 Comparison of load -displacement curves
3 有限元参数分析
3.1 高厚比影响
钢管混凝土柱肩梁边柱高厚比有限元参数分析共设置 5个模型(GHB1~GHB5),中柱试件共 5个模型(GHZ1~GHZ5).经有限元计算,边柱高厚比模型荷载-位移关系对比见图11,具体数值见表3;中柱高厚比模型荷载-位移关系对比见图 12,具体数值见表 4.通过比较发现:边、中柱肩梁的屈服荷载与极限荷载增加速度随着高厚比的减小(腹板厚度增加)而减慢.边柱肩梁腹板厚度每增大2 mm屈服荷载增加约152 kN;中柱肩梁腹板厚度每增加2 mm极限荷载增大约204 kN.但随着高厚比的减小,Py/Pu值逐渐增大,两者数值逐渐接近,将对结构的安全产生不利影响.
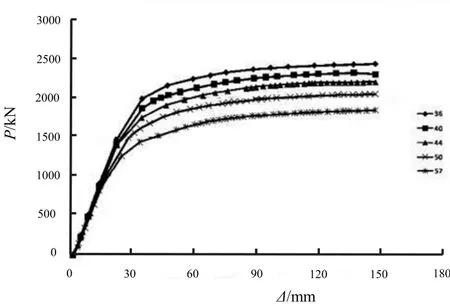
图11 不同高厚比边柱肩梁荷载-位移曲线Fig.11 Load -displacement curves of different depth-thickness ratio side column

图12 不同高厚比中柱肩梁荷载-位移曲线Fig.12 Load -displacement curves of different depth-thickness ratio middle column

表3 不同肩梁腹板高厚比边柱肩梁尺寸和荷载值Tab.3 Geometrical dimensions and loads of different depth-thickness ratio side column

表4 不同肩梁腹板高厚比中柱肩梁尺寸和荷载值Tab.4 Geometrical dimensions and loads of different depth-thickness ratio middle column
3.2 高跨比影响
钢管混凝土柱肩梁边柱高跨比有限元参数分析共设置 4个模型(GKB1~GKB4),中柱试件共 4个模型(GKZ1~GKZ4).经有限元计算,边柱高跨比模型荷载-位移关系对比见图13,具体数值见表5;中柱高跨比模型荷载-位移关系对比见图 14,具体数值见表 6.通过比较发现:边柱肩梁的屈服荷载与极限荷载增加速度随着高跨比的减小(腹板高度增加)而减慢;中柱肩梁随着高跨比的减小,屈服荷载增速基本不变,而极限荷载增速加大.可见,肩梁采用中柱布置形式,承载力提高更具明显.边柱肩梁高跨比每增加0.1,屈服荷载增加约235 kN;中柱肩梁高跨比每增加 0.1,屈服荷载增加约 284 kN.但随着高厚比的减小,Py/Pu值逐渐增大,两者数值逐渐接近,将对结构的安全产生不利影响.
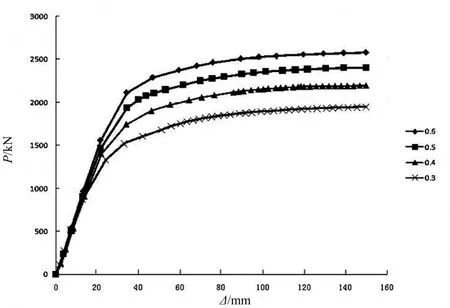
图13 不同高跨比边柱肩梁荷载-位移曲线Fig.13 Load -displacement curves of different high-span ratio side column
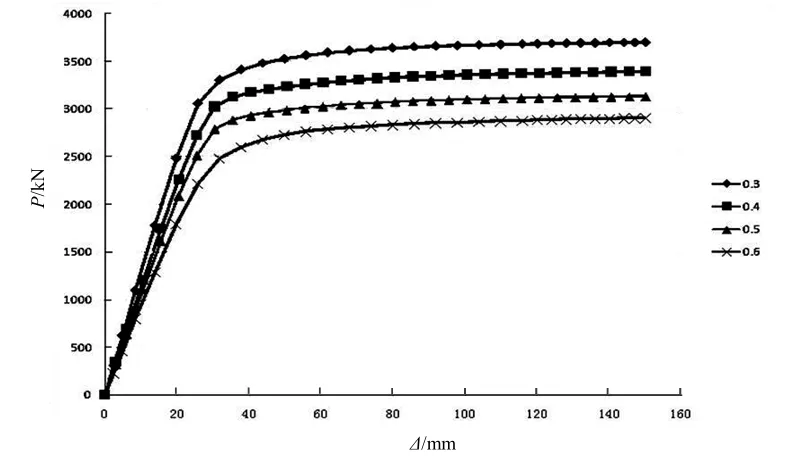
图14 不同高跨比中柱肩梁荷载-位移曲线Fig.14 Load -displacement curves of different high-span ratio middle column

表5 不同高跨比边柱肩梁尺寸和荷载值Tab.5 Geometrical dimensions and loads of different high-span ratio side column
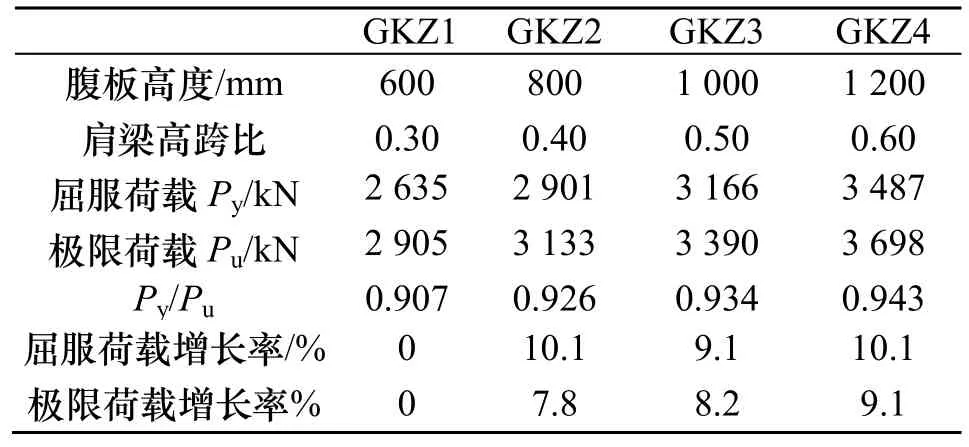
表6 不同高跨比中柱肩梁尺寸和荷载值Tab.6 Geometrical dimensions and loads of different high-span ratio middle column
4 设计方法研究
根据试验及有限元分析结果,肩梁的破坏主要由腹板受剪形成一条斜压带引起,进而导致整体结构变形过大而丧失承载力.故肩梁的承载力设计应采用考虑剪力作用下腹板受剪破坏控制的方法.剪力起控制作用下:
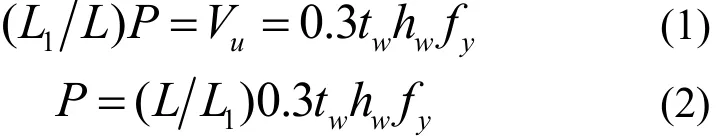
弯矩起控制作用下:
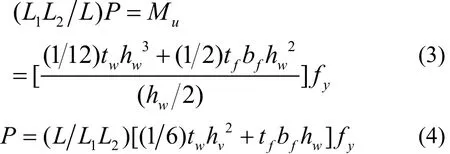
令:

当0.3≤ (hwL2)[(1 6)+()]时,剪力起控制作用.一般比值 twhwtfbf<2.0,偏于安全时,取 twhwtfbf=2.0,代入上式得:hwL2≥ 0 . 45.
肩梁在剪力起控制作用下,即 hw/L2≥0 . 45的条件下,承载力计算公式为

实用设计公式

式中:maxV 为由上柱传来的轴心力对肩梁腹板所产生的剪力;wt为肩梁腹板厚度;wh为肩梁腹板高度.
对实用公式进行验证,可靠指标 β=3.7,由于肩梁不同于其它构件,其破坏形式通常为强度破坏,为了保证其安全性,根据相关规范,肩梁的可靠度为β=3.7(理论计算结果乘以系数1.2后,与有限元计算屈服荷载进行比较),具体结果见图 15.经比较可发现:边柱和中柱肩梁按公式(6)所确定的承载力与有限元分析结果总体趋势一致,边柱的计算结果吻合较好,中柱计算结果虽然存在一定差距,但总体仍可以保证其满足可靠度要求指标.按实用公式确定的肩梁承载力可以满足设计要求.
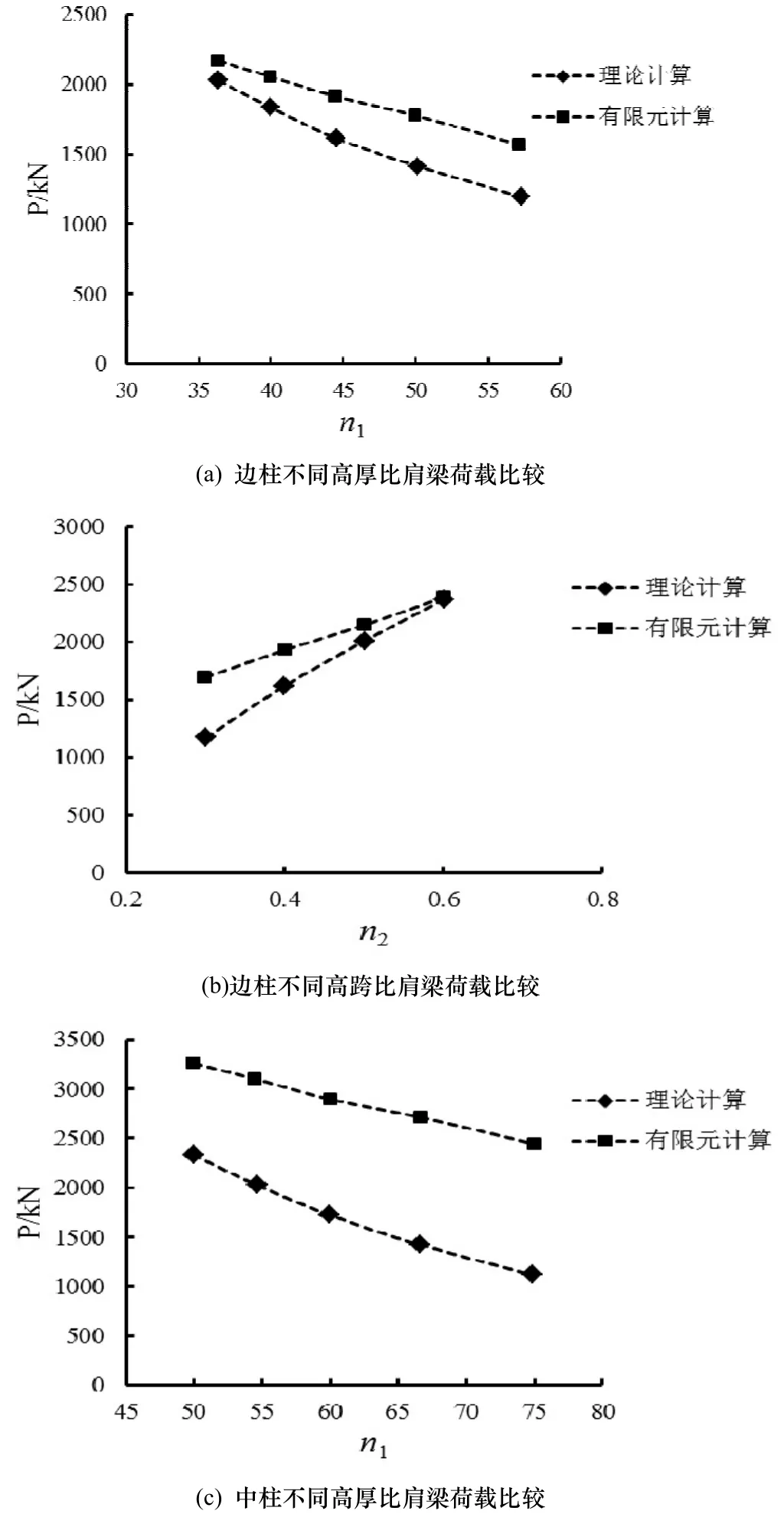

图15 计算承载力与有限元计算结果对比Fig.15 Comparison of formula and finite element calculation results
5 结论
通过对改进型钢管混凝土柱单腹板肩梁有限元分析及设计方法研究,可得到以下结论:
(1)边、中柱肩梁的屈服与极限荷载增加速度随着高厚比的减小而减慢;边柱肩梁的屈服与极限荷载增加速度随着高跨比的减小而减慢;但中柱肩梁随着高跨比的减小,屈服荷载增速不变,而极限荷载增速加大.
(2)肩梁采用中柱形式,承载力提高更具优势.但随着肩梁高厚比、高跨比的减小,Py/Pu值逐渐增大,对结构的安全产生不利影响,设计时应严格控制肩梁的高厚比与高跨比取值.
(3)肩梁的破坏主要由腹板受剪形成一条斜压带引起,进而导致整体结构变形过大丧失承载力.
(4)按考虑剪力作用下腹板受剪破坏控制的肩梁承载力实用公式可满足结构可靠度规定指标的要求.
References
[1] 于安林, 童根树. 钢管混凝土四肢柱单斜缀杆双腹板肩梁的受力性能[J].西安公路交通大学学报, 1998,18(2):36-38.YU Anlin, TONG Genshu. On bearing behaviors of single diagnial lacing double web stay member of open concrete filled steel tube with four main elements[J].Journal of Xi'an Highway University, 1998,18(2): 36-38.
[2] 于安林, 童根树. 钢管混凝土四肢柱人字形缀杆双腹板肩梁的受力性能[J].西安建筑科技大学学报:自然科学版,1998,30(2):112-114.YU Anlin, TONG Genshu. Carrying behaviors of herringbone lacing double-web stay member of open concrete-filled steel tube with four main elements[J]. J.Xi′an Univ. of Arch. & Tech.: Natural Science Edition,1998,30(2):112-114.
[3] 于安林, 童根树. 钢管砼柱肩梁研究总结及建议[J].西安建筑科技大学学报:自然科学版,1998,30(3):247-249.YU Anlin, TONG Genshu. Study conclusion and design proposal on stay member of concrete filled steel tube [J].J. Xi′an Univ. of Arch. & Tech.: Natural Science Edition,1998,30(3):247-249.
[4] 于安林, 童根树. 钢管混凝土双肢柱单腹板肩梁的试验研究和理论分析[J]. 工业建筑,1998,28(4):24-26.Yu Anlin,Tong Genshu. Test study and theory analysis on the single web stay member of open concrete filled steel tube with two main elements[J].Industrial Construction,1998,28(4):24-26.
[5] 金天德, 饶芝英. 钢管混凝土柱肩梁应力分析[J].浙江建筑,1997(5):12-15.JIN Tiande, RAO Zhiying. Shoulder beam stress analysis of concrete filled steel tube columns [J].Zhejiang Construction, 1997(5): 12-15.
[6] 沈祖炎, 郑沂. 多肢柱肩梁刚度的分析[J].建筑结构,1999,29(7):50-52.SHEN Zuyan, ZHENG Yi. Analysis of the stiffness of shoulder beams[J].Building Structure, 1999,29(7):50-52.
[7] 董振平. 钢管混凝土双肢柱肩梁受力性能与设计方法研究[D].西安: 西安建筑科技大学,2011.DONG ZhenPin. Study on Performance and Design Method of CFST Column's Shoulder Beam[D]. Xi′an:Xi′an Univ. of Arch. & Tech., 2011.
[8] GB50017-2003. 钢结构设计规范 [S].北京:中国计划出版社,2003.GB50017-2003.Code for design of Steel structures [S].Beijing: China planning press, 2003.
[9] GB50011-2010. 建筑抗震设计规范 [S].北京:中国建筑工业出版社,2002.GB50011-2010. Code for seismic design of buildings[S].Beijing: China Architecture&Building press, 2002.
[10] 苏明周, 黄智光, 王亚军, 等.钢管混凝土双肢柱改进型单腹板肩梁承载能力试验研究[J].西安建筑科技大学学报:自然科学版,2010,42(4):473-479.SU Mingzhou, HUANG Zhiguang, WANG Yajun, et al.Experimental study on the bearing capacity of improved single web shoulder beam member with double concrete-filled steel tube column[J]. J. Xi′an Univ. of Arch. & Tech.: Natural Science Edition, 2010, 42(4):473-479.

