基于GIS及改进微分进化算法的变电站选址研究
马 威,李章维,徐 毅
(浙江工业大学信息工程学院,浙江杭州320000)
0 引言
国内外在变电站选址方面已经开展了大量的研究。近年来,随着计算机技术不断进步及人工智能技术的快速发展,为变电站的选址提供了一些新思路。遗传算法、蚂蚁算法、粒子群算法等一系列智能优化算法用于解决变电站的优化选址方面,并且取得了很大进展[1-5],但这些优化算法并非尽善尽美,也存在着运算效率不高、最优解容易陷入误区、不考虑变电站实际地理情况等问题,而且单纯地把变电站选址看成是数学上的非线性规划,不考虑变电站实际地理情况,变电站很可能建立在实际上并不适合建站的位置。因此,本研究在文献[6]基础上提出改进微分进化算法及GIS 相结合新的寻址方式。
本研究首先阐述微分进化算法(DE)的原理,然后对改进微分进化算法效果进行验证,最后通过算例分析来验证规划方案的可行性。
1 微分进化算法
1.1 基本DE 算法
微分进化(DE)算法是由Kenneth Price 和Rainer Storn 为了解决切比雪夫多项式的问题而提出的一种群体智能优化算法。它可对非线性不可微连续空间函数进行最小化处理,具有高效性、收敛性、鲁棒性等优点。其算法如下[7-9]:
(1)初始化。DE 算法利用NP 个参数向量作为每一代的种群,通常情况下,初始种群是从给定边界约束内从整个参数空间里随机选取的。第g 代种群的个体可以表示为:
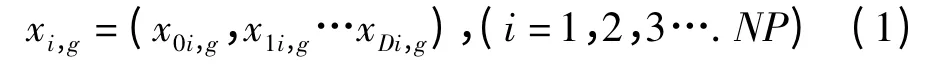
式中:D—问题解空间的维数,其中第一代的个体向量的各个分量由下式随机得到:

式中:i—个体在种群中的序列;NP—种群规模,rand为[0,1]之间的均匀分布随机数;—第i 个个体的第j 个分量的上界和下界,其中j=1,2…D。
(2)变异。对于第g 代的个体向量xi,g,其对应的变异个体向量产生如下式:
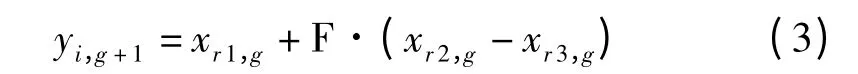
式中:r1,r2,r3∈[1,NP],且随机选择的序号r1≠r2≠r3≠i;比例系数F∈[0,2]—一个实常数因数,控制着偏差变量的放大作用。
(3)交叉。为了保持种群的多样性,就要增加干扰参数向量的多态性,引入交叉操作。试验向量变为:

式中:rand(j)∈[0,1]—一个均匀分布的随机数;rnbr(i)∈[1,D]—一个随机选择的整数,它确保zi,g+1至少从yi,g+1获得一个分量;CR∈[0,1]—交叉因数,控制选择变异个体分量代替当前个体分量的概率。
(4)选择。本研究在试验向量zi,g+1和目标向量xi,g之间通过贪婪方式进行选择。如果zi,g+1的适应度比xi,g的适应度好,那么zi,g+1将取代xi,g才进入到下一代,否则xi,g保留。对于最小化问题,选择操作可表述为:
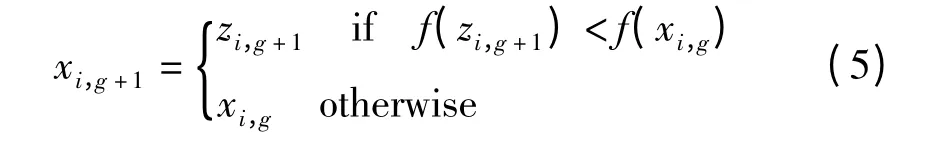
(5)参数设置。DE 算法中有3 个基本控制参数:种群规模NF、比例系数F、交叉因数CR。控制参数的选取值很大程度上影响DE 算法的搜索性能。种群数量NP 的维数最好选取在5~10 倍之间,并且NP 的数值要大于4。F 在在进化过程中取值区间一般取[0.4,0.9],而交叉因数CR 取值区间可为[0.3,0.8],它们的具体优化值依赖于目标函数的特性[10]。
1.2 改进DE 算法(IDE)
1.2.1 动态调整控制参数
在基本DE 算法中,F 和CR 一般是不发生改变的。F 和CR 会影响搜索过程的稳定性和收敛速度。F 取值较大时,可以得到较好的搜索结果,但此时算法的收敛速度会变得相对较慢;而当F 取值较小时,又会使算法陷入局部最优。
对CR 来说,过小的取值,种群在交叉操作后产生较少的新个体,减弱了算法开拓新空间的能力;过大的CR 取值,又使得种群不能很好地保持鲁棒性。所以,在基本DE 算法中,搜索到全局最优解附近时,种群多样性往往会发生改变,使搜索过程相对缓慢或因早熟而陷入局部最优。
因此,改善DE 算法性能的关键之处就是设法保持种群的多样性以及良好的选择机制,受粒子群算法中惯性权重动态调整思想的启发,本研究对F 和CR采用进化动态调整的策略[9],第i 次进化过程中Fi和CRi如下式所示:
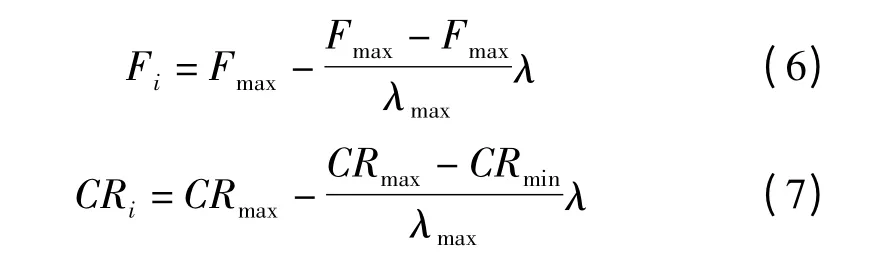
式中:Fmax,Fmin—F 设定最大值和最小值;CRmax,CRmin—CR 设定的的最大值和最小值;λmax,λ—设定的最大迭代次数与当前迭代次数。
1.2.2 改进算法的性能测试
本研究通过选取3 个经典测试函数,来测试IDE算法的性能,并与标准DE 算法进行比较[12]。这3 个函数如下:

3 个测试函数设置种群数量均为60 个,最大迭代次数1 000 次。DE7 代表DE 基本算法DE/rand/1/bin,DE 其他参数设置为:F=0.5,CR=0.4。两种算法都对3 个测试函数运行100 次,测试结果如表1所示。
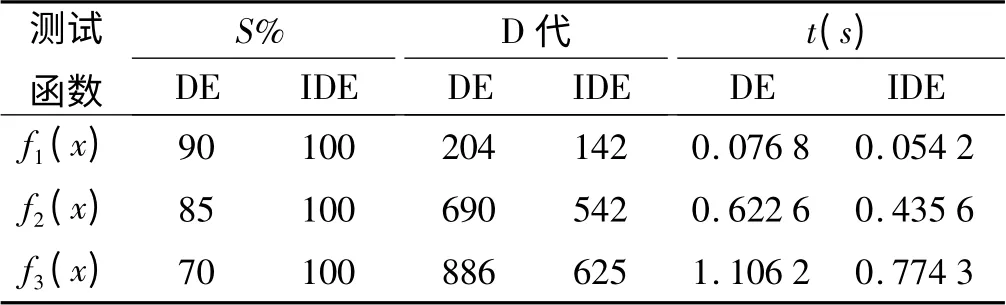
表1 IDE 与DE 算法结果比较
3 个函数的维数分别是2、10、30,它们的复杂程度逐渐增加。从表1 可以明显看出,通过动态调整F、CR的取值,IDE 算法搜索成功率明显高于基本DE 算法,并且IDE 算法在保证搜索成功率的基础上,明显降低了收敛所需的迭代次数和时间。可见,IDE 算法比DE算法的搜索效率更高,全局寻优能力更好。
2 改进DE 算法及GIS 在变电站选址定容的应用
2.1 数学建模
变电站选址的一般方法是:首先通过负荷预测,得出规划水平年的负荷需求,然后在满足规划水平年负荷需求的基础上,使变电站的初始固定投资成本、可变运行成本、网损费用最小为原则,确定待建变电站的位置,容量和供电范围。具体可以建立如下数学模型[13]:
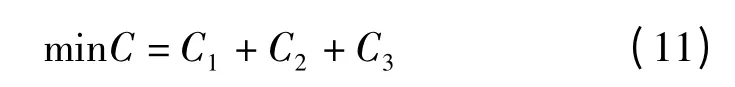
式中:C1—每年的变电站的投资及运行费用,C2—每年的变电站低压侧线综合投资年费用,C3—变电站低压侧线年网损用。

式(12~14)中:n—规划区新建变电站的个数,f(Si)—第i 个新建变电站的的投资费用,g(Si)—第i 个新建变电站的运行费用,k—贴现率或资金回收率,m—变电站的折旧年限,α—单位线路投资费用,N—已有和新建变电站的总数,j—变电站i 的一个负荷点,Ji—变电站i 供电的所有负荷点,lij—变电站i 到负荷点j 的距离,β—线路网损折算系数,Pj—负荷点j 的负荷大小。
变电站的结束条件如下式所示:

式中:Si—第i 个变电站的总容量;e(Si)—第i 个变电站的负载率;cosφ—变电站的功率因数;Ri—第i 个变电站的供电半径;qij—j 负荷点是否由i 变电站供电的标志,qij=0 表示“否”,qij=1表示“是”。
一般情况下,变电站可看作是点状实体,而变电站可建地块看成一个闭合的区域,在规划区内,先明确不可建区域,再结合市政建设规划确定可建变电站区域。研究者通过IDE 算法,得到变电站的候选坐标向量,并把这些坐标向量作为一组解,代入到目标函数中,通过考虑投资及运行费用的多少来判定变电站址的优劣。
本研究以外点法来构造适应度函数,直接将约束条件以罚函数形式计入函数中,目标函数为:

式中:λ,ω—很大的正整数,用以惩罚因子。φ 函数定义如下式所示:

2.2 GIS 中地理信息的分析处理
电网GIS 规划多采用图层来管理和存储数据,并提供多种数据可视化方式,通过将规划区域的电子地图与电网电子地图通过空间数据库进行单层或多层叠加分析,可以满足用户单层或多层叠加浏览的需要,大大提高变电站的寻优效率[14]。
本研究利用MapInfo 公司开发的MAPX 控件产品作为GIS 平台,通过对地理信息图层的查询形成空地图层,然后利用模糊综合理论对空地块进行地理、环境等因素的综合评价,最后形成规划的适用地块图层,这样要判断变电站选址的地点是否可行,只要知道该地址是否落在这个图层的适用地块内即可。地理信息处理的过程如下:
2.2.1 地理上空白地块图层的形成
根据规划区的地理情况,本研究选择变电站选址过程中要参考一些地理因素,然后再准备相应的地理信息图层文件,如湖泊、道路、建筑物、居民地等。
首先,每个地理信息图层要先设置一个条件(如建筑物图层:该图层在某一区域内没有对象)。其次,建立一个空白图层,以单位变电站的占地面积为步长,遍历整个规划区,判断在地理信息的每一个图层的地块上是否满足设定条件。如果满足的话,就在空白地图的相应位置上,创建一个单位步长的空白地块对象,并且画出空白地块。最后,检测空白地块之间的连贯性,进行对象合并,进而减少对象的个数。
2.2.2 供电地块的综合评判
在进行变电站选址时,不是所有的空白地块都能作为变电站候选范围,要考虑城市的用地规划情况、交通状况等很多因素。因此可把规划区分为多个供电地块,利用模糊综合评价理论,评价每个地块是否可以作为变电站选址的适应值。
模糊综合评判的数学模型可表示如下:假设评价涉及到的p 个因素集合是U={u1,u2,…,up},并且n个评定语的集合可为V={v1,v2,…,vn}。由实际情况来看,评语集合可取为{很适宜,适宜,一般,不太适宜,不适宜}。若第i 个因素对第j 种评语的隶属度可用rij来表示,则可用评价矩阵R 来表示因素论域与评语论域之间的模糊关系:

式中:0≤rij=μR(ui,vj)≤1,i=1,2,…p。
全面评价对象的时候,要考虑到所有的p 个因素。但做最后结论时,各个因素的参考价值却是不一样的。因此,在进行评价之前,应考虑到各种因素的权重,可看成是因素集U 的模糊子集A=(a1a2…ap)(0≤ai≤1,i=1,2,…m),并把A 与R 的合成B 看作综合各种因素后,而对被评对象做出的最终评价,即模糊综合评判。因此模糊综合评判的数学模型可表示为:
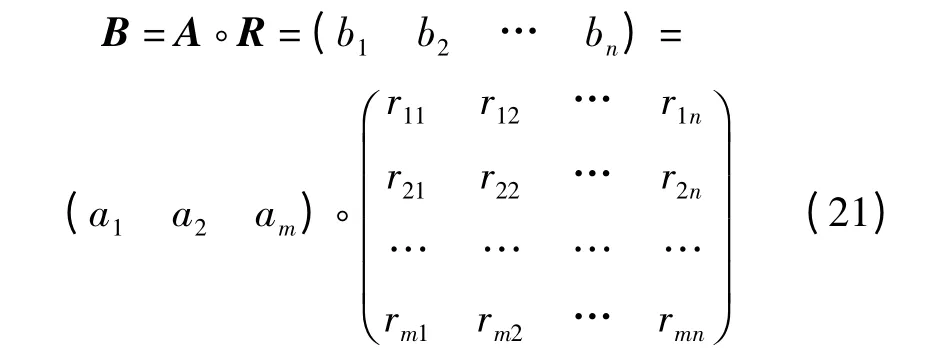
式中:“·”—模糊运算符,该运算符不同的定义对应着4 种不同的模糊综合评判模型。在判断某个地块是否为变电站适用地块的时候,不仅要考虑影响选址的主要因素,也要关注次要的因素,所以选择了加权平均模型,其中bj的计算如下式:
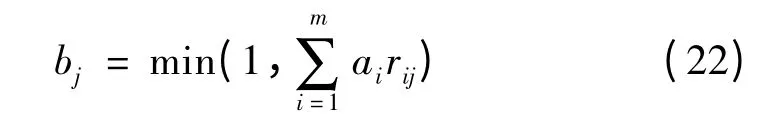
据此,整体模型可表示为:
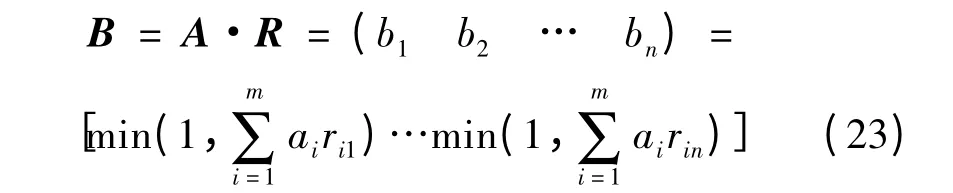
2.2.3 通过图层整合形成适用地块
通过2.2.1 节与2.2.2 节得到了2 个图层:一个是空白地块的图层,另一个是有评判分值的供电地块图层,然后,需要对这2 个图层进行综合,以便找到最合适的变电站候选地块,具体方法为:以空白地为线索,把空白地块位置在供电地块的评分,叠加到空白地块的数据表上,这样每个空白地块就是带有适应分值的地块了,通过设定评分值条件,能选择其中的一些地块作为变电站选址的可行性地块,然后删除图层中其他对象,这样就能得到规划区域内变电站的可建区域。
2.3 基于改进DE 算法及GIS 的变电站选址
变电站选址定容的步骤如下[15]:
(1)初始化算法参数(变量维数D、种群数量NP,比例系数F 和交叉因数CR 的范围等),根据规划区的变电站可选容量及规划年的负荷总量确定变电站数量、容量;
(2)随机初始化DE 群体个体位置(变电站落点);
(3)根据地理信息,判断变电站落点的可行性,并且把落点在不可行区域内的个体,按照就近原则重新给定位置;
(4)对种群个体进行变异操作;
(5)对种群个体进行交叉操作;
(6)对变异交叉后的种群,根据个体位置,判断变电站落点的可行性,并把落在不可行区域的落点重新给定位置;
(7)利用就近原则,把负荷分配给各变电站,,再由变电站所带负荷大小确定其容量等因素。利用式(18)计算个体适应度,并找出全局极值点xgbest;
(8)判断算法是否收敛,若收敛,输出全局极值点xgbest和对应变电站容量及所带负荷,搜索结束;若不收敛,转向步骤(4),重新执行后续步骤。
3 算例分析
某地规划区域面积为48.4 km2,该次规划基准年取2014年,规划年到2025年,基准年的最大负荷为76.68 MW,负荷预测后,得出规划水平年的最大负荷为153.2 MW,等效集中负荷点共有134 个。本研究参照《城市电力规划规范》的规定,结合该区实际情况,得到规划区的负荷分布预测结果,2025年该地区分类负荷预测结果如表2所示。

表2 规划区分类负荷预测结果
考虑到当地供电公司和该区发展要求,可对已有两座变电站进行增容,并将规划区的东侧地块作为规划新区;到2025年,着重发展一类负荷,逐步形成居民居住区、工业园区。因此可考虑在该区域新建变电站。根据城市电力网规划设计导则,容载比可取1.8~2.1,可确定规划年变电站总容量范围为273.24~318.78 MVA,故可将已有变电站增容到2 ×35 MVA,并新建两座2 × 40 MVA 的变电站,此时总容量为300 MVA,规划区的容载比为1.96,满足电网规划导则,保证电网运行的科学性和经济性。
变电站地理信息中考虑的图层有:公路,河流,建筑物,居民地等,地块评估涉及的因素有交通因素、经济因素、地质因素、用地性质等,目标函数参数设置如下:功率因数cosφ=0.8;资金贴现率k=0.08;变电站综合投资为28 万元/MVA;变电站运行费用为0.6万元/MW,资金回收年限25年,网损折算系数为0.18,单位线路的投资费用α=50 万元/km;惩罚因子λ=420 万元。IDE 算法的参数设置:种群规模50,最大迭代次数500 次,最大比例系数Fmax取0.7,最小比例系数Fmin取0.2,最大交叉因数CRmax为0.8,最小交叉因数CRmin为0.4。
以式(18)为目标函数,在未考虑地理信息的情况下,变电站规划结果如图1所示。
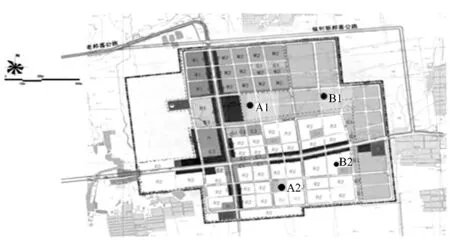
图1 未考虑地理信息基于IDE 的变电站规划结果
在未考虑地理信息时,变电站的落点可能会落在道路、湖泊等一些不可建站区域,当在考虑地理信息时,就可以避免出现这类问题,使得规划结果更加合理。采用IDE 算法,考虑地理信息,用地性质等建站综合因素后,规划站址如图2所示。

图2 考虑地理信息基于IDE 的变电站规划结果
对比图1 可知,已有变电站A1,A2位置不发生改变,并且新建变电站B1位置也不变,而变电站B2地理位置有所变化,未考虑地理因素时,B2落在规划道路上,这显然是不符合规划要求的,考虑地理因素时,基于GIS 和IDE 进行规划,B2落在了公共绿化地块,使规划结果更加可行、实际,由此得到的最优经济方案的目标函数值为5 896 万元。
4 结束语
本研究通过规划区实际算例分析,得到如下结论:
(1)改进微分进化算法计算速度快、全局寻优能力强,与DE 算法相比,具有较好的综合寻优能力。
(2)利用模糊综合评判理论对供电地块的各种因素进行综合评判,产生适用地块,为变电站选址定容提供了良好的地理数据基础。
(3)本研究在分析变电站选址时,综合考虑了建站投资、线路投资和网络运行费对站址的影响,并把地理信息融入到IDE 算法中去,使得规划结果更加合理,科学。
[1]王成山,刘 涛,谢莹华.基于混合遗传算法的变电站选址定容[J].电力系统自动化,2006,30(6):30.34,47.
[2]付 郁.基于放进遗传算法的某发动机T 装配线平衡研究[J].机械,2014(5):16-21.
[3]赵 强,敬 东,李 正.蚁群算法在配电网规划中的应用[J].电力自动化设备,2003,23(2):52.54.
[4]武从猛,王公宝.遗传一蚁群算法在目标分配问题中的应用研究[J].兵工自动化,2014(4):12-15,25.
[5]刘自发.张建华.基于改进多组织粒子群优化算法的配电网络变电站选址定容[J].中国电机工程学报,2007,27(1):105-1l1.
[6]牛卫平,刘自发,张建华,等.基于GIS 和微分进化算法的变电站选址及定容[J].电力系统自动化,2007,31(18):82-86.
[7]STORN R.System design by constraint adaptation and differential evolution[J].IEEE Trans on Evolutionary Computation,1999,3(1):22-34.
[8]PATER S,GOSWAMI S K,GOSWAMI B,Differential evolution algorithm for solving unit commitment with ramp constraints[J].Electric Power Components and System,2008,36(8):771-787.
[9]刘自发,闫景信,张建华,等.基于改进微分进化算法的电力系统无功优化[J].电网技术,2007,31(18):68-72.
[10]杨丽徙,王家耀,贾德峰,等.GIS 与模糊模式理论在变电站选址中的应用[J].电力系统自动化,2003,27(18):87-89.
[11]徐毅虎.基于地理信息和改进微分进化算法的变电站优化规划[D].北京:华北电力大学,2012
[12]许童羽,孙艳辉.基于GIS 和改进微分进化算法的农网变电站选址定容[J].电力系统保护与控制,2009,37(22):34-39.
[13]赵光权,彭喜元,孙 宁.带局部增强算子的微分进化改进算法[J].电子学报,2007,35(5):849-853.
[14]刘自发,张 伟.基于地理信息因子及自适应小生境微分进化算法的变电站规划[J].电力自动化设备,2012,32(10):42-47.
[15]刘清海,杨建华,杨 普,等.农村电网变电站优化规划[J].农机化研究,2010(2):199-202.

