风电机组耦合系统的模态分析
程传玉
(中国电建集团昆明勘测设计研究院有限公司,云南昆明650051)
0 引言
风力发电作为新型绿色能源一直受到国家高度重视,截止到2013年底,全国累计装机量达80 GW[1],在总装量方面保持全球领先的地位。然而国内风电机组运行稳定性及发电效率并不理想,由于风电机组由多个子系统耦合组成,且设计准确性、材料质量、装配及安装工艺合理性等问题的存在,机组设计与现场情况存在一定的偏差,耦合振动故障是机组安全运行重大隐患。
根据GL 规范和行业振动标准要求,为了保证风电机组安全运行,要求机组各主要结构件固有频率及激振频率不产生交叉或重合现象,如无法避免,要求采取相应的措施,保证机组快速通过交叉点,且通过时振幅达到有效控制,避免发生耦合共振现象,但未给出机组及部件模态分析方法和固有频率推荐值[2-4]。
目前,国内外研究风电机组模态特性普遍基于分析力学、多体力学、有限元分析方法[5-8],通过仿真模拟或实验室方法对机组和主要部件进行模态分析。然而风电机组长期处于恶劣的现场环境中运行,多部件柔性耦合,且各个子系统边界连接条件复杂、交叉影响,缺乏现场实测数据,很难仅通过仿真模拟或实验室方式得到风电机组可靠的模态特性参数[9-10]。
因此,本研究针对风电机组设计上如何避免耦合共振的问题,以兆瓦级风电机组为研究对象,采用拉格朗日法建立机组动力学方程,解耦得到整机模态参数,随后展开机组风场实测工作,获取实测模态参数,同时研究理论模型及子系统边界简化方式是否符合现场实际情况、理论数据与实测数据偏差及开展机组稳定性分析。
1 动力学模型建立
风电机组低频振动主要为3 种形态:风轮、机舱和塔架耦合轴向(前后)振动;风轮、机舱和塔架耦合横向(左右)振动;风轮、机舱和塔架耦合扭转振动[11-14]。整机耦合振动模型如图1所示。以下简单简述3 种振动形态产生的机理:
(1)机组横向(左、右)耦合振动,主要激振源为:风轮质量分布不平衡和风轮气动力不平衡产生横向力分量;机舱质心不在轴线上产生偏心力等。
(2)机组轴向(前、后)耦合振动,主要激振源为:湍流、阵风等风速波动引起的风轮推力变化;竖直方向上风切变引起的载荷差异等。
(3)机组扭转耦合振动,主要激振源为:风向波动引起的载荷波动;横向风切变引起的载荷差异等。
在自然风况下,风电机组以轴向(前、后)耦合振动最为严重,该耦合振动可分解为塔架耦合系统前、后方向运动和风轮系统在旋转面外俯仰运动。

图1 整机耦合振动模型
本研究采用拉格朗日法建立机组动力学方程,首先定义广义坐标零点为整机质心,x 轴为机组轴向方向,y 轴为机组左右方向,z 轴为竖直向上;然后定义桨叶、轮毂和塔架坐标系如图2所示;最后定义风轮系统前后方向位移量为χz,桨叶变形角为β,桨叶弹性变形为γ,塔架耦合系统的前后变形位移为yz,风轮转速为ω,外部风载为F。
考虑到两个子系统的模态方程跟各自惯性矩、边界连接刚度及约束条件有关,故合理简化耦合系统模型边界连接条件不仅可以使问题简单化,又可反映出耦合运动的规律。考虑到桨叶、轮毂、机舱和塔架的结构特性和长宽比,故假设桨叶和塔架为质量集中在中心轴上的弹性梁,轮毂和机舱为质量集中的刚性块;轮毂和主轴、机舱和塔架均为刚性连接,地基为刚性基础[15-16]。首先建立风轮系统动力学模型,如式(1~3);其次建立塔架耦合系统动力学模型,如式(4);最后联立两个子系统方程获得耦合系统动力学方程:

式中:m1—单片桨叶质量,kg;m2—轮毂系统质量,kg;m3—机舱质量,kg;m4—塔架质量,kg;l—机舱长度,m;w—机舱宽度,m;r—塔架顶部半径,m;t—塔架顶部壁厚,m;S—单片桨叶质量矩,kg·m;α—风轮系统锥角,°;I—单片桨叶转动惯量,kg·m2;E—弹性模量,Pa;ω—风轮系统转速,rad;ct—塔架阻尼系数;cn—机舱阻尼系数;kn—机舱刚度系数,N/m;Sz—桨叶和机舱质量矩,kg·m;g—重力加速度,m/s2;h—塔架高度,m;L—整机质心到轮毂中心距离,m。
利用风轮前、后方向位移变形和塔架耦合系统前后方向位移变形的一致性,即χz=yz,联立方程(1~4)获得整机动力学方程:

式中:


机组固有频率是系统固有特性,与质量、刚度和阻尼有关,考虑到空气粘滞阻尼对整机影响很小,故可忽略阻尼影响。因此,令[C]=[0],{F}={0},则式(5)可简化为:

令

把式(7)代入式(6)求解得主阵型矩阵[A],然后对刚度矩阵和质量矩阵进行解耦可得:

则式(8)可化简为:
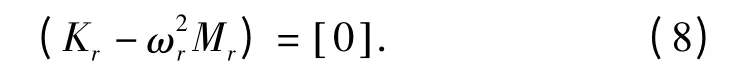
式中:Kr—第r 阶模态刚度,Mr—第r 阶模态质量,ωr—第r 阶模态频率。
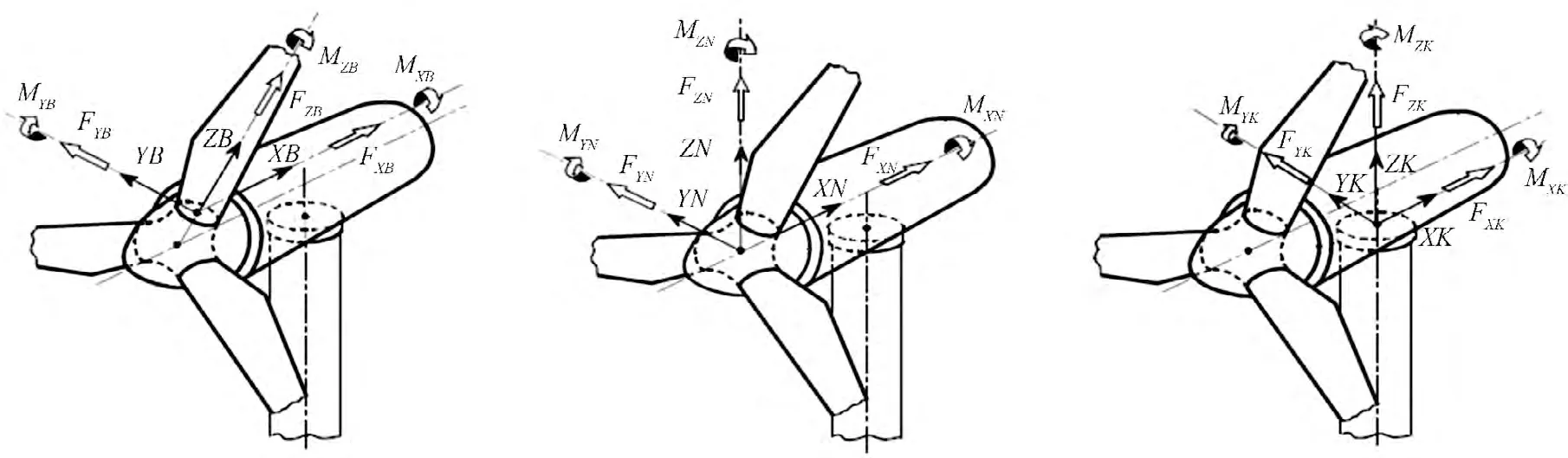
图2 风电机组桨叶、轮毂和塔架顶部坐标系
本研究以1 500 kW 变速变桨双馈机型为计算对象,轮毂中心高度70 m,风轮直径82 m,桨叶长度40.3 m,风轮转速范围9.9 r/min~17.4 r/min,额定转速17.4 rpm。输入1 500 kW 机组刚度矩阵[K]和质量矩阵[M]参数,求得机组固有频率如表1所示。

表1 机组固有频率
2 机组现场测试
2.1 风轮系统测试
考虑到动力学模型是假设各子系统刚性连接的情况下建立的,而现场桨叶通过变桨轴承连接至轮毂上,连接刚性有一定程度的下降。为了准确获得风轮系统现场情况下的固有频率,本研究选取云南省大理市某1 500 kW风场23#机组展开现场测试。笔者任意选择机组某片桨叶,在离桨叶叶根约20 m 处挥舞和摆阵方向各安装一个ICP 加速度传感器(频响范围0.2 kHz~10 kHz),采用24 位AD/102.4 kHz 数据采集仪,参数设置:采样频率:32 Hz,谱线数:6 400 线,分辨率:0.005 Hz。采集桨叶桨距角分别在0°和90°两种情况下受自然风载激励的响应数据,测试结果如图3、图4所示。

图3 23#机组桨叶桨距角0°方向挥舞和摆阵频谱图

图4 23#机组桨叶桨距角90°方向挥舞和摆阵频谱图
当桨距角在0°时,挥舞方向动态响应数据较为明显,从图3 中可知,其主要尖峰频率为塔架耦合系统前后一阶固有频率为0.4 Hz,风轮系统一阶挥舞频率为0.75 Hz,塔架耦合系统扭转一阶频率为1.05 Hz,风轮系统一阶摆阵频率为1.325 Hz。当桨距角为90°时,摆阵方向动态响应数据较为明显,从图4 可知,其主要尖峰为塔架耦合系统前后一阶固有频率为0.4 Hz,风轮系统一阶挥舞频率为0.8 Hz,塔架耦合系统扭转一阶频率为1.075 Hz,风轮系统一阶摆阵频率为1.375 Hz。
2.2 塔架耦合系统测试
考虑到动力学模型是在假设地基为刚性的情况下建立的,而现场机组地基刚度受土壤条件、灌注方式、钢筋水泥结构等影响。为了准确地获得塔架耦合系统现场情况下的固有频率,笔者采用24 位A/D 转换卡数据采集仪,参数设置:采样频率:32 Hz,谱线数:6 400线,分辨率:0.005 Hz。分别在离塔架顶端约0.5 m处,爬梯和与爬梯成90°夹角方向上各安装一个ICP加速度传感器(频响范围0.2 kHz~10 kHz),在机组运行工况(风速约10 m/s~14 m/s 波动)中采集振动数据。结果如图5所示,塔架耦合系统前、后和左、右一阶固有频率约为0.42 Hz。
3 数据分析
3.1 数据比对与分析

图5 23#机组塔架耦合系统前、后和左、右方向频谱图
根据动力学模型计算结果可知,机组一阶模态振型主要表现为塔架耦合系统前后方向俯仰运动,机组二阶模态振型主要表现为风轮系统挥舞方向(旋转面外)运行,机组三阶模态振型主要表现为风轮系统摆阵方向(旋转面内)运动。
理论模型数据与实测数据比对如表2所示,从表2 可知,整机动力学模型理论计算数据与现场实测数据偏差均在10%以内,两者具有较好的一致性。这说明整机动力学模型及边界连接条件简化方式基本符合现场实际情况,具有较高的可靠性。

表2 理论模型数据与实测数据比对
3.2 整机稳定性分析
根据耦合系统实测数据可知,风轮转频1P 为0.165 Hz~0.29 Hz,3P 为0.495 Hz~0.87 Hz,塔架耦合系统前、后和左、右一阶固有频率约为0.420 Hz;风轮系统一阶挥舞频率约为0.750 Hz,风轮系统一阶摆阵频率约为1.375 Hz。
风电机组坎贝尔图如图6所示,风轮转频1P、3P与塔架耦合系统一阶固有频率,风轮系统一阶摆阵频率相距甚远,不存在交叉或重合现象,当风轮转速为15 r/min 时,风轮3P 与风轮一阶挥舞频率有交叉点。由于机组额定转速为17.4 r/min,15 r/min 为机组升速区过程某节点,故机组控制策略在该节点采用增加传动链阻尼和快速通过相结合方式有效控制机组通过该节点时振动能量,从而保证机组安全稳定运行,符合工程设计及运行要求。

图6 风电机组坎贝尔图
4 结束语
随着兆瓦级风电机组大型化发展,塔架高度不断增加,系统刚度下降,且各子系统边界连接刚度下降。因此,可能存在塔架耦合系统受到风轮转频1P、3P 或风轮系统挥舞、摆阵频率激励,导致机组耦合共振的现象,本研究通过建立整机动力学模型和现场实测工作,得到以下结论:
(1)耦合系统动力学模型计算结果与实测数据偏差均在10%以内,数据具有很好的一致性。说明耦合系统动力学模型及各子系统边界连接条件简化方式符合现场情况,具有较高的精准性,为机组研发、设计和优化提供理论指导依据。
(2)利用所建理论模型和实测数据对该款机型进行稳定性分析,验证了该塔架耦合系统一阶固有频率、风轮转频1P、3P 与风轮系统一阶摆阵固有频率不存在交叉与重合现象。仅当风轮转速为15 r/min 时,风轮3P 与风轮系统一阶挥舞固有频率存在交叉。由于该节点为机组加速区间段,机组制策略在该节点采用增加传动链阻尼和快速通过相结合方式有效控制机组通过此节点时振动能量,从而保证机组安全稳定运行,符合工程设计及运行要求。
[1]李俊峰.中国风电发展报告2013[M].北京:中国环境科学出版社,2013.
[2]Germanischer Lloyd.Guideline for the Certification of Wind Turbines Edition 2003/2004[S].Hamburg:Germantis cher Lloyd,2003.
[3]全国风力机械标准化技术领会.GB/T 19072—2003,风力发电机组塔架[S].北京:中国标准化出版社,2003.
[4]全国风力机械标准化技术领会.GB/T 25383—2010,风力发电机组风轮叶片[S].北京:中国标准化出版社,2010.
[5]THOMAS G C,ARLO N.Modal testing of a rotating wind turbine[R].SAND82-0631 Sandia:Sandia National Laboratories,1983.
[6]WRIGHT A D,KELLEY N D,OSGOOD R M.Validation of a Model for a Two-bladed Flexible Rotor System:Progress to Date[C]//Proceeding of the 37th AIAA Aerospace Sciences Meeting and Exhibit.Reno Nevada.[s.n],1999:293-307.
[7]LEE D,HODEGS D H,PATIL M J.Multi-flexible-body dynamic analysis of horizontal axis wind turbines[J].Wind Energy,2002(5):281-300.
[8]GENTILE C A.Ambient vibration testing of historic masonry towers for structural identification and damage assessment[J].Construction and Materials,2007,21(6):1311-1321.
[9]何玉林,黄 伟,李成武,等.大型风力发电机传动链多柔体动力学建模与仿真分析[J].机械工程学报,2014,50(1):61-69.
[10]王 峰,方宗德,李声晋.多载荷工况下人字齿轮传动系统振动特性分析[J].振动与冲击,2013,32(1):49-52.
[11]贺德馨.风工程与工业空气动力学[M].北京:国防工业出版社,2006.
[12]TONY B.风能技术[M].武鑫译.北京:科学出版社,2007.
[13]李本立,宋宪耕,贺德馨,等.风力机结构动力学[M].北京:北京航空航天大学出版社,1999.
[14]李 金,袁 魏.对转风力机的设计及流场数值模拟[J].流体机械,2013(5):22-28.
[15]周 进,房 宁,郭 鹏.基于相对主元分析的风电机组塔架振动状态监测与故障诊断[J].电力建设,2014,35(8):125-129.
[16]刘亚昆,吴兴伟.风力发电机组振动故障及信号分析技术综述[J].沈阳工程学院学报,2014,10(4):298-301.

