基于PCA-BP算法的汽车涂装线烘房系统故障诊断研究*

叶永伟，叶连强，钱志勤，任设东

(浙江工业大学机械工程学院，浙江杭州310014)

0 引言

汽车涂装线由前处理系统、电泳系统、烘房系统等组成，是一个具有不确定性、繁杂多变的对象。对涂装线设备参数进行可靠、准确地监测和潜在故障的及时预警和诊断是保证各系统设备稳定运行的基本条件。其中，如何从采集到的原始数据中提取最显著的特征，并通过特征参数对设备故障及时在线预警和诊断是机电设备信号特征提取、状态监测的关键技术［1］。

特征提取是分类器设计前对原始特征进行筛选的过程，合适的特征提取方法对后续的分类器设计有很大帮助。目前特征提取研究方法多，邵衍振等［2］提出一种基于提升小波包变换变化公式，给出移频算法，选择合适的小波进行提升小波包变换来提取状态特征向量。张家良等［3］提出一种非线性频谱特征与核主元分析相结合的设备故障参数提取方法，解决因非线性频谱数据量庞大，无法直接检测与分类的困难。统计特征提取方法中的主成分分析法(principal component analysis，PCA)［4-5］广泛地应用在参数特征提取中。谭啸峰等［6］采用PCA 算法对空间手写字符轨迹进行平面处理，成功将空间手写识别问题回归平面手写识别问题。张小桃等［7］对影响过热气温的12 个过程变量的运行数据进行主元分析，确定过热器喷水流量是引起过热汽温变化的主导因素。刁广州等［8］引入动态可调主元分析法，解决了复杂产品制造过程中由多元质量数据自相关引起的大量虚发报警问题。

设备故障诊断技术涉及的学科领域广，主要分为基于数学模型的方法、基于知识的方法和基于信号处理的方法三大类［9-10］。基于神经网络的诊断方法，诊断实质是建立从征兆到故障部件的映射过程。BP 神经网络广泛用于解决复杂、高度非线性问题，但是存在收敛速度慢，易陷入局部极值的缺点［11］。基于专家系统的故障诊断方法是利用领域专家在长期实践中积累起来的经验建立知识库，并设计一套计算机程序模拟人类专家的推理和决策过程进行故障诊断。李增芳［12］实现了以神经网络推理为主的多种人工智能技术集成的发动机故障诊断测试专家系统。基于信号处理的故障诊断是利用各种信号处理方法进行分析处理，提取相关故障信号的时域与频域特征用于故障诊断，主要包括小波变换方法和谱分析方法［13］。

本研究结合PCA-BP 方法，实现原始特征参数双重降维和诊断过程不易陷入局部极值的效果，研究分析汽车涂装线烘房系统设备故障频发的问题。首先，笔者给出PCA 建模原理及降维改进过程，然后给出BP 算法具体改进步骤，最后以烘房加热系统为例，验证该方法的可行性。

1 PCA 建模原理及模型改进

1.1 设备监测参数PCA 建模

设某个过程监测，有n 组样本点m 个变量的样本集合矩阵为X(X∈Rnxm)，协方差矩阵为∑(∑∈Rnxm)。则相应的PCA 模型数据矩阵为Xn×m，其中行表示一组样本，列表示设备监测过程变量。

为消除不同变量不同量纲的影响，需要对X 进行标准化处理，为了书写方便，标准化后的矩阵仍记为X。其标准化公式为:

其PCA 建模过程如下:

(1)计算X 的协方差矩阵:

(2)计算∑的m 个特征值λ1≥λ2≥…≥λm，以及对应的正交特征向量P1，P2，…，Pm;

(3)求取主元向量Y 为:Y=XP;

其中元素Yh为:

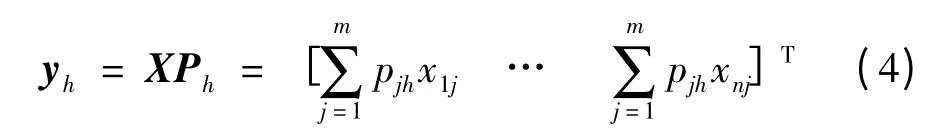
式中:Pjh—主轴Ph的第j 个分量。

(4)计算各主成分的贡献率和累积贡献率:

贡献率:

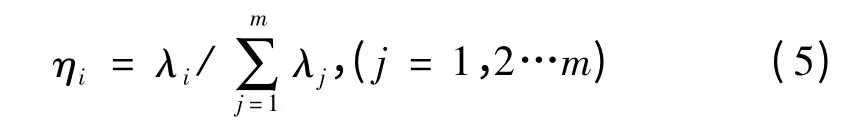
累积贡献率:

式中:λi—数据矩阵X 的协方差矩阵∑的特征值，且λ1≥λ2≥…≥λm≥0。工程上要求βk在85%以上，可以认为已求的k 个主成分可以反映原数据足够多的信息，可确定主成分个数为k。

(5)利用公式(4)来进行提取前k(k ＜m)个主成分，得到压缩后的向量，即各方向主成分yk。

1.2 PCA 模型改进

经过以上处理后，可用k(k ＜m)个主成分来表示原有数据的信息，各主成分降维模型:

式中:X—特征向量，X=(x1，x2，…，xm);Pi=(Pi1，Pi2，…，Pim)表示主成分系数向量。各主成分是原来特征参数的线性组合，可知监测参数空间并没有得到降维。为使监测空间得到降维，综合考虑主成分贡献率ηi和各特征对主成分贡献程度的大小，对模型改进:

(1)对主成分系数向量进行取正，取正后仍记为Pi=(|Pi1|，|Pi2|，…，|Pim|)，并对特征影响程度大小排序;

(2)由前k 个主成分贡献率ηi，优先考虑贡献率大的主成分，找出对主成分的影响程度大的特征参数，剔出不重要的特征;

(3)去除特征之后的各维数和原特征进行对比分析，找出最佳维数。

原模型通过改进后，剔出影响不大的特征量，缩小原始特征监测空间，同时用k(k ＜m)个主元来表示原始信息，达到双重降维的效果。

2 BP 算法

2.1 BP 算法原理

BP 神经网络由输入层、隐层和输出层构成，其模型结构简单而被广泛用于工程中。BP 算法的本质是梯度下降法，是一种局部搜索的优化方法。当BP 算法用于求解复杂的非线性函数的全局极值，就很有可能陷入局部极值，导致训练失败。因此需要对BP 算法作出改进。

2.2 BP 算法的改进

BP 算法改进具体步骤如下:

(1)预设网络各连接权值，试运行神经网络，生成训练样本，计算网络输出误差函数E(t);

式中:η+，η－—增加因子、减小因子，且满足0 ＜η－＜1 ＜η+，通常取η－=0.5，η+=1.2;∂E(t)/∂wji—指标函数E(t)对权值wij的梯度。

(4)计算网络权值的调整公式，如下式所示:

改进后的BP 算法抛开了传统算法中偏导数大小的概念，而采用偏导数符号的改变来调整网权值，有效避免了BP 算法容易陷入局部极值的缺陷。

3 实验分析与讨论

汽车涂装线烘房系统由燃烧加热、热风循环以及废气处理3 个子系统组成，本研究以烘房燃烧加热系统为研究对象，建立其PCA 特征提取模型，通过BP 网络进行故障诊断。设备监测结构如图1所示。

图1 烘房加热系统参数监测

3.1 基于PCA 的烘房燃烧加热系统分析

根据现场需要，烘房加热系统需测定的特征参数如表1所示。

表1 烘房燃烧加热系统特征参数

现本研究从烘房燃烧加热系统运行的历史数据中提取38 组样本，包含表1 的全部17 个指标。对原始数据标准化处理，并在Matlab 中进行PCA 分析，绘制结果如图2所示。

图2 PCA 各主成分贡献率和累积贡献率

17 维特征对前8 个主成分的影响程度如图3所示，各系列对应各主成分。横坐标表示17 维特征变量，纵坐标表示各特征对主成分影响程度值。根据图中的特征影响程度排序，排除影响不大的特征，采取占用主成分的比例和主成分贡献率多少的方法，选择最佳的维数，选取结果如图4所示。

图3 各特征对主成分的影响程度图

从图4 中得出，系列6 在第8 个主成分的贡献率处出现陡变，与原来的贡献率差别大，说明此处已丢失一些数据信息，故11 维指标会丢失过多的数据信息不可选;系列5 在第8 个主成分之后的主成分贡献率越来越小，主要的贡献率都来自前8 个主成分，在选择最佳维数时，优先考了处理空间维数，也缩减了监测空间维数。

图4 降维效果比较图

基于以上分析，燃烧加热系统的最佳监测维数为12 维，其特征为删除第6、8、13、14、17 特征的其余特征。这样通过采用主成分分析法即降低了处理空间维数，也缩减了监测空间维数。

3.2 BP 模型的建立及故障诊断

根据PCA 降维分析结果，本研究将提取12 维在线监测参数作为BP 神经网络输入模型。根据烘房加热系统故障经验分析，系统可能发生故障:调节阀阻塞Q1、输送管道堵塞Q2、燃气水分含量过多Q3、助燃风机压力不足Q4、原油含水Q5、电机转子故障Q6，建立6 维的网络输出层模型。隐层节点数m 根据经验公式确定，取m=13。构建烘房加热系统BP 神经网络诊断模型如图5所示。

图5 烘房系统网络模型

网络模型确立后，本研究对其进行充分的训练，神经元激活函数全部取对数Sigmoid 函数。具体的训练步骤如下:

(2)计算网络可变参数对网络误差的一阶偏导数∂E(t)/∂wij，并根据式(8)计算;

“颜晓晨，这里有空位！”沈侯站起来，冲她招手，示意她过去。在同学们诡异的目光下，颜晓晨挤了过去，坐到沈侯旁边，“你怎么没坐最后一排？”

(4)计算所有样本的误差平方和err，t=t+1，如果err＜g 或t ＞e，则训练结束，否则跳到步骤2。

网络参数设置如下:

目标误差:g=10－3;

最大循环次数:e=2 000;

最大权更新值:Δmax=50.0.

设置好各参数后，使用Matlab 软件对其进行建模、训练，在模型达到预设的要求以后，运用到实际实验中去。该次实验测得有效数据38 组，选取其中5 组样本进行故障诊断分析，各监测点源数据如表2所示。并由式x*=(x－xmin)/(xmax－xmin)进行数据的归一化处理，处理结果如表3所示。

表2 各监测点源数据

表3 源数据归一化处理后数据

本研究将表3 中的样本数据分别输入已训练的改进BP 算法，得到实际输出值如表4所示。

表4 改进BP 算法故障诊断输出值

表4 中，输出节点分别对应6 种故障类型，每组样本数据对应6 种输出，取值分0、1，其中0 表示系统状态对应项处于正常，1 表示系统设备出现故障。如样本3节点1 输出值为1，说明系统该时刻可能出现调节阀阻塞问题，而样本1 则说明此时输送管道堵塞，这两种情况都表明系统出现了故障。根据BP 网络输出值得到系统最终诊断结果，各组样本对应的系统状态如表5所示。

表5 各组样本对应的系统状态

4 结束语

本研究将PCA 应用于涂装线设备信号特征提取中，通过初步降维使得缩减后的特征在保证信息丢失最少的前提下，充分反映设备运行状态;通过二次降维，缩减了监测变量的维数，使得结果更优。笔者将降维后的监测样本特征作为改进BP 网络的输入参数，达到诊断过程收敛速度快、不易陷入局部极值的良好效果，并实现了对烘房加热系统的故障诊断。

［1］何正嘉，曹宏瑞，訾艳阳，等.机械设备运行可靠性评估的发展与思考［J］.机械工程学报，2014，50(2):171-186.

［2］邵衍振，曹建军，王艳霞，等.提升小波包变换及在振动故障诊断中的应用［J］.科学技术与工程，2008，8(15):4095-4098.

［3］张家良，曹建福，高 峰，等.结合非线性频谱与核主元分析的复杂系统故障诊断方法［J］.控制理论与应用，2012，29(12):1558-1564.

［4］TURE M，KURT I，AKTURK Z.Comparison of dimension reduction methods using patient satisfaction data［J］.Expert System with Applications，2007，32(1):422-426.

［5］TAMURA M，TSUJITA S.A study on the number of principal components and sensitivity of fault detection using PCA［J］.Computers and Chemical Engineering，2007(31):1035-1046.

［6］谭啸峰，沈海斌.基于主元分析的空间手写平面化预处理技术［J］.机电工程，2011，28(8):965-969.

［7］张小桃，倪维斗，李 政，等.基于主元分析与现场数据的过热汽温动态建模研究［J］.中国电机工程学报，2005，25(5):131-135.

［8］刁广州，赵丽萍，要义勇.动态可调主元分析的多元自相关质量控制方法［J］.西安交通大学学报，2013，47(3):24-29.

［9］高 伟，李 春，叶 舟.基于滑移网络的H 型垂直轴动态气态特性分析［J］.流体机械，2013，41(10):36-40.

［10］周东华，胡艳艳.动态系统的故障诊断技术［J］.自动化学报，2009，35(6):748-758.

［11］丛 爽，向 微.BP 网络结构、参数及训练方法的设计与选择［J］.计算机工程，2001，27(10):36-38.

［12］李增芳.基于人工智能和虚拟仪器技术的发动机故障诊断专家系统研究［D］.杭州:浙江大学生物系统工程与食品科学学院，2004.

［13］张 萍，王桂增，周东华.动态系统的故障诊断方法［J］.控制理论与应用，2000，17(2):153-158.