基于响应面法的鱼类饲料颗粒密度预测模型研究

■宋 欣 李艳聪 万志生 李艳琳 郑爽爽

（1.天津农学院工程技术学院，天津300384；2.天津市世昌科技发展有限公司，天津301508）

科学合理的饲料加工工艺是保证饲料适口性、改善消化率和提高动物生产性能的关键。其中，颗粒饲料加工质量的评价指标主要有颗粒大小、含水率、粉化率和硬度等。但是鱼类不同于畜禽类，其消化器官比较简单而且较短，消化肠长度只相当于猪的1/10，而且鱼类的摄食方式、摄食环境也不同于畜禽，因此就要求水产饲料要更易消化，而且其颗粒形状、大小和水中沉浮性必须与鱼的大小、种类和自然采食习惯相适应。由于饲料密度决定了饲料在水中的沉浮特性，并且对生产能力、饲料外观和喷涂物的吸收效果等指标均有影响，因此常被作为评价水产颗粒饲料质量的关键指标之一。影响饲料颗粒密度的因素有很多，如成型工艺及参数、成型设备结构参数、饲料原料与配方等，但目前国内外文献中对于饲料颗粒密度的研究很少，仅局限于对其影响因素和控制方法的定性分析，或者从饲料原料和配方角度分析对密度的影响，而在成型设备和工艺参数的影响方面研究甚少，仅有李艳聪等（2006）中对制粒机颗粒密度特性与环模结构间的关系进行了研究，并建立了环模、压辊结构参数和粉料密度、颗粒料密度间的映射关系模型。但该模型中没有考虑成型工艺参数的影响。另外，吴劲峰等（2007）通过环模制粒试验得出了苜蓿草粉制粒挤出力与粒度、制粒密度间的关系。连潇等（2012）中以苜蓿草粉制粒密度为试验指标，进行了挤出力、含水率及草粉粒度的正交试验，确定出了草颗粒产品成型工艺的最优参数组合。上述研究成果对于本研究的开展具有一定的借鉴意义。

为此，本文采用响应面试验设计方法，对颗粒密度与压缩比、压制速度之间的影响规律进行研究分析，旨在实现饲料颗粒密度的预测，以及为成型设备主要结构参数优化和成型工艺方案的选择提供理论依据。

1 颗粒压制试验装置

该颗粒压制试验装置用于模拟颗粒饲料在环模孔中的成型过程。主要由孔径模具、加压柱、加热电阻丝、外套、顶盖和底座构成(见图1)。其中，核心部件是孔径模具，为可更换件，不同模具具有不同的孔径和孔深。试验中通过更换模具，即可达到改变模孔压缩比(孔径/有效孔深)的目的。此外，为了考虑温度对颗粒性能的影响，在装置中嵌入了加热电阻丝和温控元件。

试验时将此试验装置放在电子万能试验机上，通过试验机控制进料的压力和速度，由试验机的顶杆推动加压柱，对粉状饲料进行施压，实现饲料颗粒的成型。

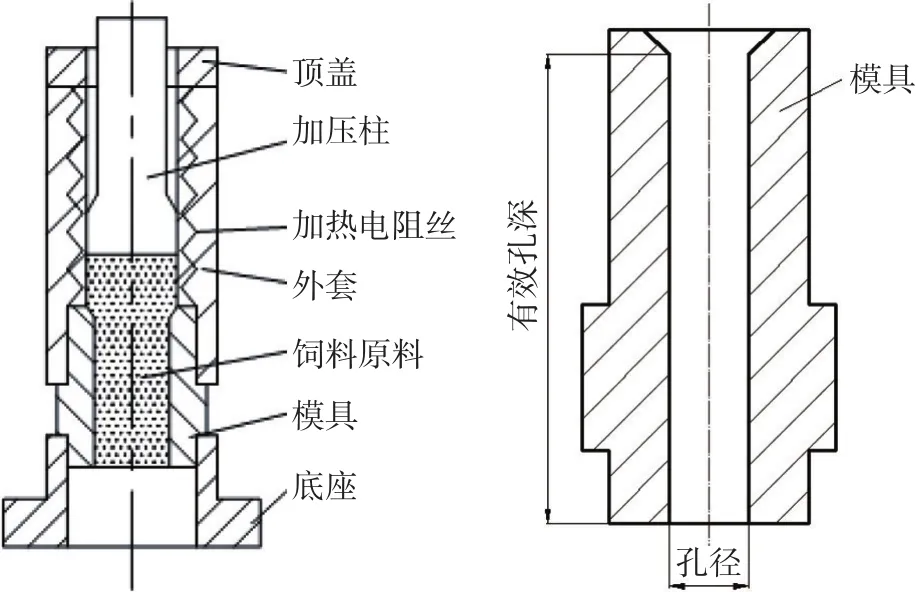
图1 颗粒压制试验装置

2 材料与方法

2.1 试验材料

试验选用的粉料是鲫鱼颗粒料原料，其粉料配比见表1。由于鲫鱼习惯生活在水面的中下层，需要饲料颗粒具备良好的下沉性，因此，该饲料颗粒密度要大于水面生活鱼类的饲料颗粒密度。

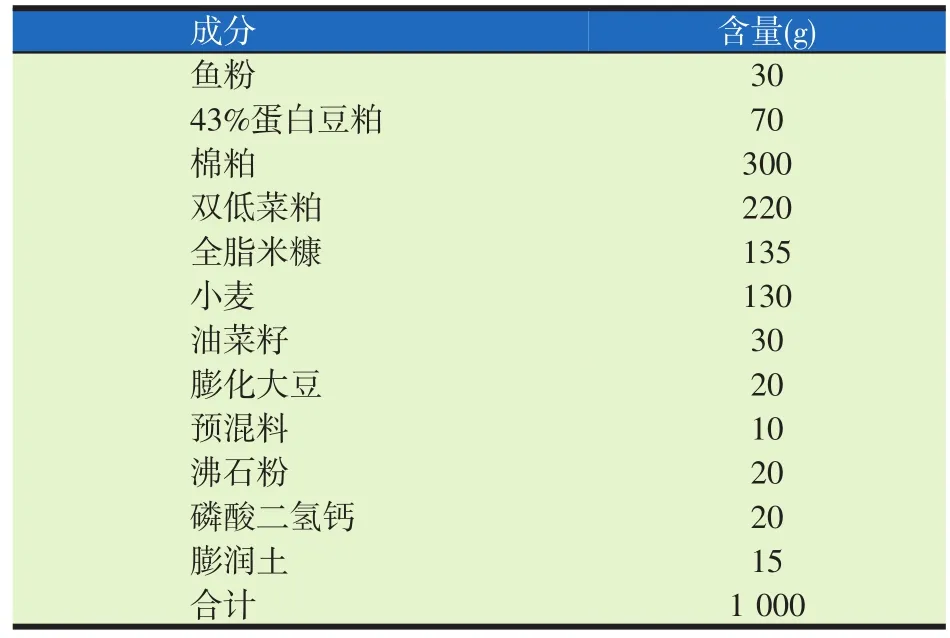
表1 粉料配方

2.2 试验设备

颗粒压制试验装置、电子万能试验机(美斯特CMT6502型)、游标卡尺(精度：0.01 mm)、分析天平(精度：0.1 mg，量程：100～300 g)、量筒。

2.3 响应面法试验设计

2.3.1 响应面试验方案：模具选用鱼类饲料压制普遍使用的模孔尺寸Φ2 mm。根据不同的压缩比要求，对应不同的有效孔深，如表2所示，压缩比越大，有效孔深越深。试验中，以饲料颗粒密度为响应值，以压制速度和压缩比为影响因子，采用中心复合实验设计(central composite design，CCD)，确定2因素5水平共25个试验点的试验方案。

表2 不同压缩比下的有效孔深

影响因子的取值范围及各自水平确定如下：鱼类饲料压制成型中，环模压缩比通常为1∶10～1∶18，如果此值过低，会导致饲料颗粒的致密度和耐水性不好，而过大则会容易造成出料难甚至塞料现象，因此试验中将压缩比分别设置为1∶10、1∶12、1∶14、1∶16和1∶18五个水平。压制速度决定了粉料在模具中的压制时间和流动速率，将其分别设定为2、4、6、8、10 mm/s五个水平。

此外，对于试验装置温度的设定，通常粉碎后的原料经调质进入环模制粒前的物料温度要求达到85～91℃，因此为了模拟的真实性，将试验装置的加热温度设定为90℃，并且在模拟压制的过程中，制粒温度始终保持在这一温度。

2.3.2 饲料颗粒密度计算：参考杨俊成等(2000)中蹾实后表观密度的测量方法：首先，在量筒中装入200 cm3饲料并进行蹾实(蹾实的目的是为了尽量减少物料内的空隙)。然后，测定量筒内饲料的质量和体积。最后，计算蹾实后的表观密度，等于量筒内饲料质量/量筒内饲料体积，单位为g/cm3。

2.4 结果与分析

按照试验方案重复做两次，得到两组试验结果，如表3所示。选取第一组试验结果，得到饲料颗粒密度Y与压缩比A、压制速度B的二阶响应面回归模型：

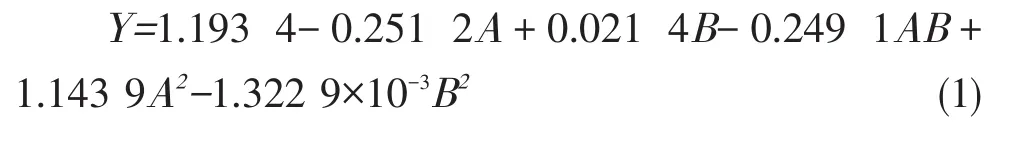
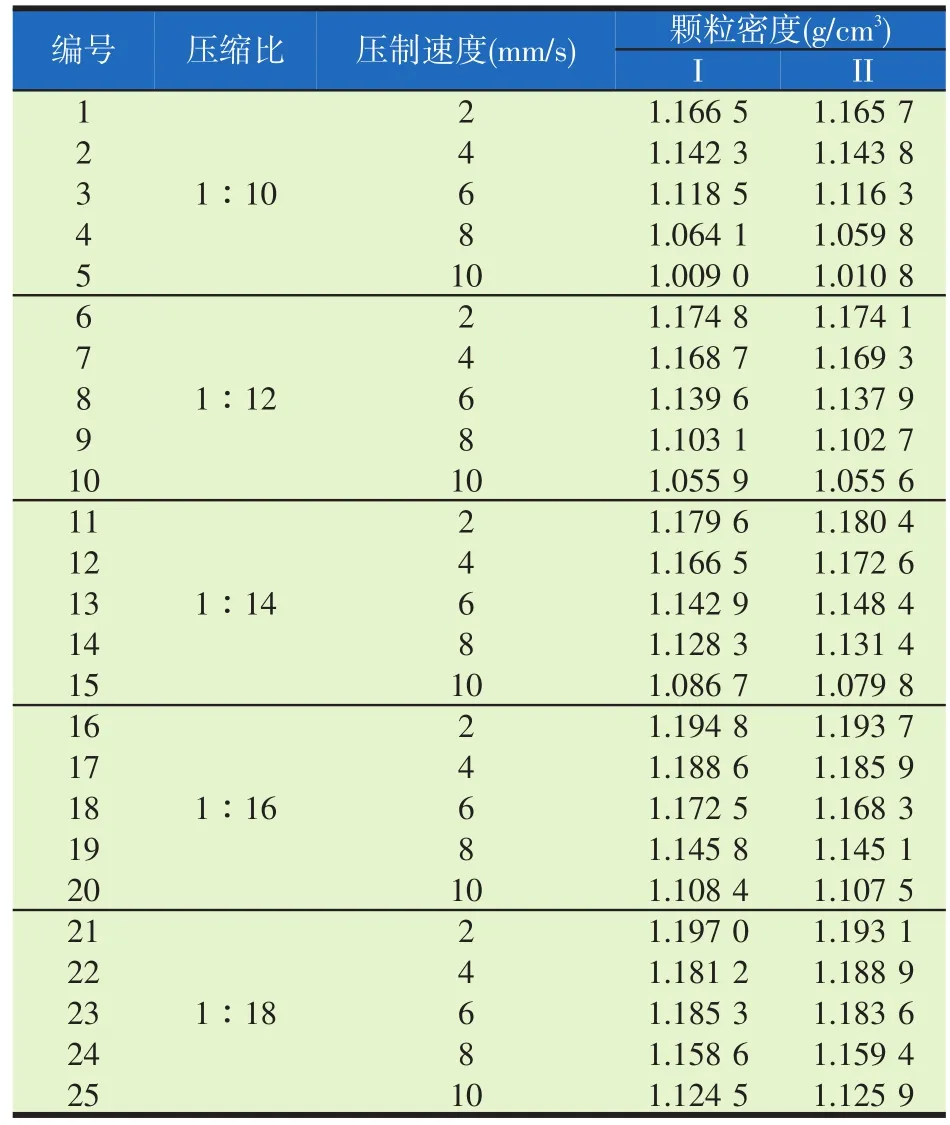
表3 饲料颗粒密度与压制速度、压缩比关系试验结果

响应面回归模型的方差分析如表4所示，回归模型的F值为334.12，P<0.000 1，差异极为显著，证明试验是可靠的。模型决定系数R2=0.988 8，校正决定系数Adj R2=0.985 8，表明模型可以解释98.58%的响应变化，模型拟合度高，试验误差小，能够很好的描述各影响因子与响应值之间的关系。依据回归模型中的系数和方差分析可知，响应面试验范围内各影响因子的主效应关系为：压制速度>压缩比>压制速度和压缩比的交互作用。

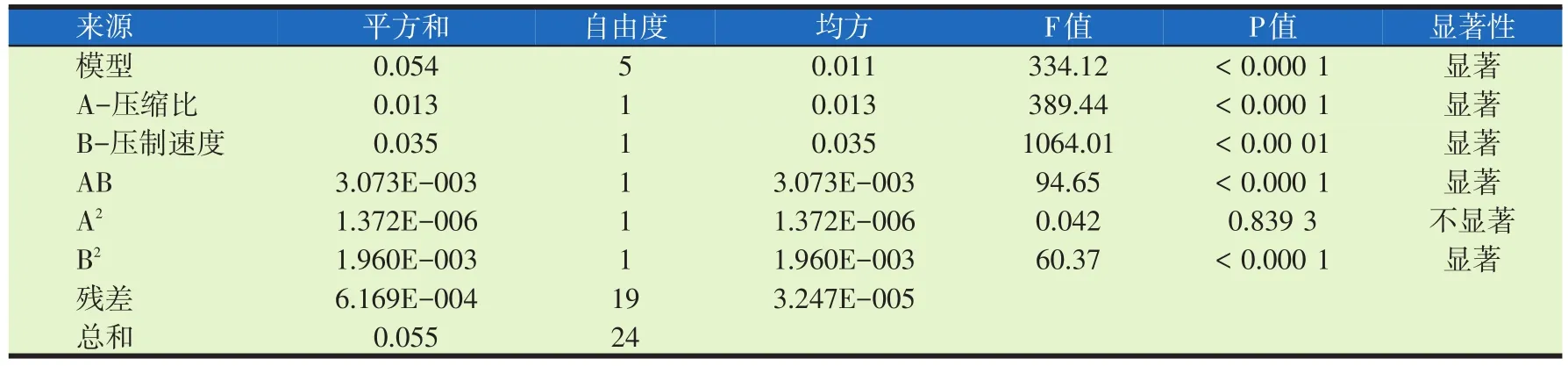
表4 回归模型的方差分析

2.4.1 单一影响因子对饲料颗粒密度的影响分析

图2中的平滑曲线由二阶响应面回归模型得到，图中散点为影响因子各水平下的试验结果。其中图2(a)为压制速度6 mm/s时，压缩比对颗粒密度的影响，可以看出当压制速度一定的情况下，颗粒密度随压缩比的增加而提高；图2(b)为压缩比为1∶14时，压制速度对颗粒密度的影响，可以得到当压缩比一定的情况下，颗粒密度会随着压制速度的提升而降低。上述结论与生产中的实际情况相符。

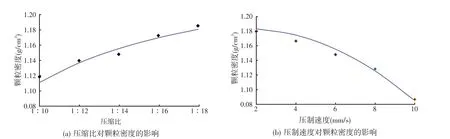
图2 单一因素对饲料颗粒密度的影响

2.4.2 影响因子交互作用下对饲料颗粒密度的影响

图3分别用响应曲面和等高线图两种方式表达了影响因子交互作用下对颗粒密度的影响，图中圆点为试验数据。响应曲面坡度越陡峭，表明响应值对于影响因子的改变越敏感；反之曲面坡度越平缓，影响因子的改变对响应值的影响也就越小。图3(a)直观地反映了压缩比和压制速度交互作用对颗粒密度的影响程度。图3(b)中显示，当颗粒密度一定时，选用环模的压缩比越小，所需设置的压制速度则越慢；反之，压缩比越大，压制速度则需要相应提高。较低的压制速度和较高的压缩比作用下可获得高颗粒密度，反之，较高的压制速度和较低的压缩比作用可获得低颗粒密度。从等高线的变化趋势来看，当压缩比增加到一定数值后，压制速度的变化将不再会对颗粒密度产生显著的影响。根据该等高线图，可以确定出获得某指定颗粒密度所需的压缩比和压制速度的选择范围，并且可以制定出多种压制速度和压缩比组合的压制方案，为成型设备结构参数优化以及工艺参数设置提供理论依据，或者根据现有的压制速度和压缩比组合方案，预测出所获得的饲料颗粒的密度。

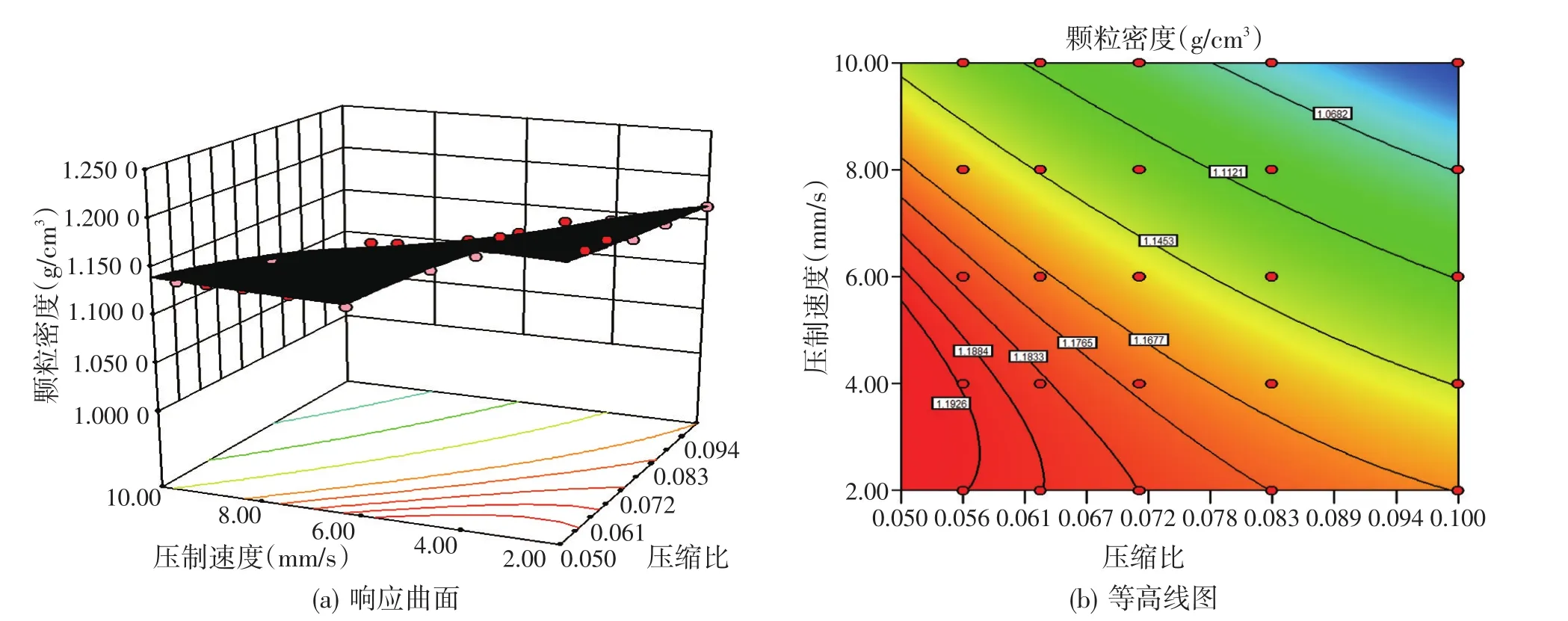
图3 影响因子交互作用下对饲料颗粒密度的影响

3 预测模型准确性验证

利用第II组试验数据进行二阶响应模型预测准确性验证，结果如表5所示。预测结果与试验结果的相对误差率在0.024 5%～0.675 9%之间，平均误差率为0.247 3%。由此可知，该二阶响应回归模型具备一定的准确性，可以在生产实践中用于颗粒密度的预测、成型设备结构参数优化以及工艺方案的选择。

表5 预测效果验证

4 结论

本文以饲料颗粒密度为响应值，以环模压缩比和压制速度为影响因子进行了鱼类颗粒饲料的压制模拟试验。依据试验结果拟合出饲料颗粒密度的二阶响应面回归模型，基于该响应面模型分析出了因子单一作用和交互作用下对饲料颗粒密度的影响。此外，还利用另一组试验数据对该模型的准确性进行了验证，结果表明该模型可以用于饲料颗粒密度的预测、成型设备主要结构参数优化和工艺方案的选择，具有一定的应用价值。