基于改进矩阵束算法的水轮机控制系统参数辨识
刘俊敏,李兴源,王 曦,丁理杰
(1.四川大学电气信息学院,成都 610065;2.四川电力科学研究院,成都 610065)
0 引言
随着电力系统的规模越来越大,运行状态越来越复杂,电网安全及其稳定运行问题的重要性也日益突出。水电机组的运行状况对维持电网频率的稳定和安全至关重要,水轮机控制系统参数的设置不当将严重影响水电机组调频功能的发挥,因此对水轮机控制系统参数的辨识是不容忽视的[1]。
目前,针对连续系统直接进行参数辨识存在的微分信号不易获得且对其近似处理会加剧噪声的问题[2],专家学者们进行了广泛的研究。常用的参数辨识方法有最小二乘法、prony算法等。基于最小二乘法的参数辨识需对连续的时间系统进行离散处理,存在原理和计算方面的误差,使得辨识结果不准确。而 prony算法由于其系统模态阶数难以确定,所以辨识过程复杂且结果不能尽如人意[3-5]。
近年来,矩阵束算法被广泛应用于连续系统参数辨识,且在电力系统分析和控制及信号处理等多个领域的应用中取得了不错效果。矩阵束算法采用内积形式,有较强的抗噪能力,且其运算属于非迭代过程,不存在迭代解法中初值限定、累积误差及高运算量等问题,是一种高效实时的计算方法[6-7]。文献[6]利用矩阵束算法实现对同步电机参数的准确辨识,文献[7]利用改进的矩阵束算法对电力系统振荡模态进行分析研究,提高参数辨识的精度,减少计算量。本文将改进矩阵束算法进行拓展,将其应用于水轮机控制系统的参数辨识中,在 Matlab中编制辨识程序,并基于Simulink模型仿真对水轮机控制系统进行参数辨识。结果表明,改进矩阵束算法在对水轮机控制系统参数辨识方面是精确快速的。
1 水轮机控制系统模型[8]
水轮机调节系统是由水轮机控制系统和被控制系统组成的闭环系统[8],结构如图1所示。
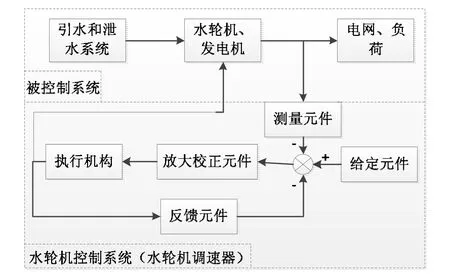
图1 水轮机调节系统结构框图
水轮机控制系统由调速器系统和水轮机及其引水系统组成。调速器模型模拟导叶开度的动作情况,以此通过水轮机及其引水系统模型仿真得到输出功率。
近年来,国内水轮机调速器的主导调节规律多采用以并联PID为基础的调节规律,随动系统采用两级放大的机械液压随动系统,调速器及随动系统模型框图如图2所示。

图2 调速器及随动系统模型
图2 中,Fg为频率给定值;Ft为机组频率;Yg为开度给定值;Pg为功率给定值;P为机组功率;Ef为人工频率死区;KP、KI、KD分别为比例、积分、微分增益;bp为永态调差系数;Tn为微分时间常数;Ty为主接力器反应时间常数;Ty1为中间接力器反应时间常数;G为导叶开度输出。
原动机模型采用简单水轮机模型,水轮机及其引水系统模型结构框图如图3所示。

图3 水轮机及其引水系统模型
图3 中,eh,ey分别为水轮机转矩的水头传递系数和接力器行程传递系数,eqh,eqy分别为水轮机流量的水头传递系数和接力器行程传递系数,通常取eh=1.5,ey=1.0,eqh=0.5,eqy=1.0;TW为引水系统水流惯性时间常数;mt为功率输出。
2 基本原理
2.1 矩阵束原理
矩阵束算法可以用于从系统的扰动响应中直接提取与信号有关的信息,如信号的频率、相位、幅值等[9]。
矩阵束算法采用等间距采样点,设观测到的系统响应为y(kΔt),其离散时间的函数形式为:
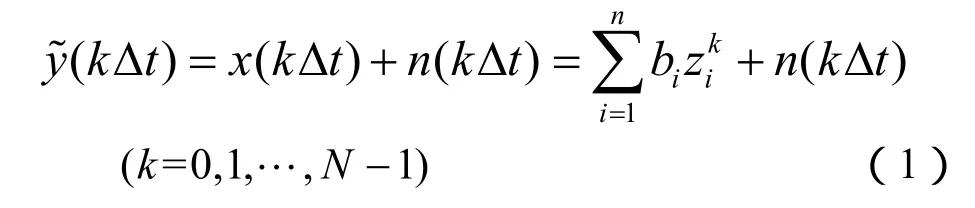
式中:x(kΔt)为不含噪声的响应;n(kΔt)为系统噪声;N为采样点数;Δt为采样间隔。
将y~(kΔt)作为实际采样点y(kΔt)的近似。式(1)中,假定bi和zi为复数,即

式中:Ai为幅值;θi为相位,rad;αi为衰减因子;fi为振荡频率。
步骤1:由采样序列y(kΔt)构造(N-L)×(L+1)阶Hankel矩阵Y,L为矩阵束的参数,恰当的选取L可以有效地抑制噪声干扰,通常L=N/ 4—N/3。
步骤2:对矩阵Y进行奇异值分解

式中:S为(N-L) × (N-L)的正交矩阵;D为(L+ 1 )×(L+ 1 )的正交矩阵;V为(N-L)×(L+ 1 )的对角阵,其对角元素σi即为Hankel矩阵的第i个奇异值。
对于不含噪声的信号,Y有L+1个奇异值σi,将其中非零值按下标由小到大构造一个非增序列。从σi中筛选出最大值σmax,若满足σi/σmax≥μ,则可将最大模态数记为n=i,式中μ为设定的阈值。由V的前n个奇异值形成的新矩阵为

式中,V'为(N-L)×n矩阵,前n行是由Y的前n个非零奇异值组成的n×n方阵,后N-L-n行全为0 。
步骤 3:取矩阵D的前n个主导右特征向量构成(L+1)×n的矩阵D',删去D'的最后一行形成L×n的矩阵D1,删去D'的第一行形成L×n的矩阵D2。定义

Y1和Y2为2个(N-L)×L阶矩阵。
由Y1和Y2组成矩阵束Y2-λY1,并求解其广义特征值,即求解

式中:为Y1的伪逆矩阵。
矩阵束Y2-λY1的广义特征值记为λi(i= 1 ,2,3,… ,n),利用矩阵相关原理可知,此特征值即为采样信号的极点。
步骤4:根据式(6),可计算得到参数b。

步骤5:利用式(2)、(3)可计算出各分量的幅值、相位、衰减因子和频率。
2.2 改进的矩阵束算法
Hankel 矩阵Y中的奇异值iσ越小,则所能反映的信息量越少,因此为降低复杂程度,引入信息熵来确定模态阶数。将奇异值iσ所占的比重定义为pi,则奇异值的信息熵可以表示为

奇异值σi越小,其所占比重pi越小,从而信息熵H(Y)迅速收敛至有界值。当取到奇异值σm时,信息熵H(Y)最接近有界值,此时模态阶数可以设定为n=m。
3 基于改进矩阵束算法的参数辨识方法
利用改进矩阵束算法辨识水轮机控制系统参数的步骤如下。
步骤1:对水轮机控制系统模型施加扰动信号,对输出信号进行采样。
步骤2:确定改进矩阵束算法中的模态阶数。
步骤 3:利用改进矩阵束算法对采样数据进行运算,确定采样信号的极点,留数等特征量。
步骤4:利用得到的特征量对调速系统各参数进行辨识。
系统辨识的基本流程如图4所示。

图4 参数辨识流程图
4 模型仿真实例
本文通过matlab/simulink建立图2、图3所示的水轮机控制系统模型,遵循GB/T9652.1-2007《水轮机控制系统技术条件》、GB/T9652.2-2007《水轮机控制系统试验规程》的标准,设定调速系统各参数值如下:Ef=0.06%,KP=1.28,KI=0.285,KD=1.25,Tn=0.28s,bp=0.02,Ty=0.65s,Ty1=0.5s,TW=2.0s。水轮机稳定运行于95%出力工况,55s时通过一次调频使水轮机出力减少 10%,为了验证改进矩阵束算法对噪声的抑制能力强及辨识精度高的特点,进行三组对比试验,其中两组在输入信号中加入高斯白噪声,分别采用改进矩阵束算法和 prony算法对水轮机控制系统参数进行辨识。辨识结果如表1所示。
由表1可知,在加噪声与不加噪声两种情况下,改进矩阵束算法的辨识值均与系统真实值很接近,误差均在5%以下,表明该方法对干扰具有较强的抑制能力。而同在加噪声情况下,改进矩阵束算法的辨识精度远高于prony算法的辨识精度。

表1 水轮机控制系统参数辨识结果
将表1的三种辨识结果分别代入到模型中进行仿真,导叶开度输出和功率输出曲线如图5和图6所示,图中曲线1为实际系统输出结果,曲线2为理想情况下改进矩阵束算法辨识得到的参数模型的仿真输出结果,曲线3为加噪声时改进矩阵束算法辨识得到的参数模型的仿真输出结果,曲线4为加噪声时prony算法辨识得到的参数模型的仿真输出结果。

图5 导叶开度输出

图6 功率输出
从图5和图6可以看出,系统输出功率的变化规律与导叶开度的动作情况一致,且曲线2、3与曲线1基本一致,利用改进矩阵束算法得到的辨识模型的仿真输出曲线与系统的实际输出曲线基本吻合,模型的整体辨识精度很高,且由曲线3、4的仿真输出结果可知,改进矩阵束算法在高斯噪声干扰下的参数辨识结果更贴近实际。
5 结语
改进矩阵束算法利用奇异值分解和矩阵的低秩近似等方法,对噪声干扰有较强的抑制能力,适合应用于实际工程中,且能较为容易且有效地确定模态阶数,提高辨识的效率和精度。
改进矩阵束算法在水轮机控制系统参数辨识方面的应用还是首次,经本文检验了其有效性,从而丰富了水轮机控制系统模型参数辨识方法。
[1]龚强, 吴道平.水轮机控制系统参数辨识与系统建模测试简介[J].江西电力, 2011, 35(3):36-39.
[2]李超顺, 周建中, 雷慧, 等.基于 Hartley变换的水轮机调速器参数辨识[J].大电机技术, 2009, 3:57-61.
[3]芦晶晶, 郭剑, 田芳, 等.基于Prony方法的电力系统振荡模式分析及PSS参数设计[J].电网技术,2004, 28(15):31-34.
[4]刘红超, 李兴源. 基于 Prony辨识的交直流并联输电系统直流阻尼控制的研究[J]. 中国电机工程学报, 2002, 22(7):55-57.
[5]戚军, 江全元, 曹一家.电力系统传递函数的通用Prony辨识算法[J].中国电机工程学报, 2008,28(28):41-45.
[6]朱瑞可, 李兴源, 赵睿, 等.矩阵束算法在同步电机参数辨识中的应用[J].电力系统自动化, 2012,36(6):52-55.
[7]李宽, 李兴源, 赵睿, 等.基于改进矩阵束的高压直流次同步振荡检测[J].电网技术, 2012,36,(4):28-132.
[8]魏守平.水轮机调节系统仿真[M].武汉:华中科技大学出版社, 2011.
[9]王宇静, 于继来.电力系统振荡模态的矩阵束辨识法[J].中国电机工程学报, 2007, 27(19):12-17.

