一种天波超视距雷达电离层相位污染的校正算法

于文启,陈建文,杨春山

(1.空军预警学院研究生管理大队,湖北武汉430019;2.空军预警学院,湖北武汉430019)

0 引言

天波超视距雷达(Over-the-Horizon Radar,OTHR)工作在3～30 MHz高频频段,利用电离层后向返回散射传播机理,对地平面以下的目标进行检测。电离层的时变不规则运动会对回波信号的相位路径进行调制,在长相干积累的情况下目标信号和杂波在多普勒域展宽,严重影响了OTHR对低速海面目标的检测性能。因此使回波谱锐化、校正电离层调制带来的相位污染就显得尤为重要。

目前已存在很多方法用来从展宽的杂波谱中提取电离层相位污染信息,第一种是在时域上将回波数据分为若干短序列,可以利用低阶多项式来估计相位,如基于匹配傅里叶变换的方法[1]和分段多项式相位建模法[2];第二种是利用标校信号自相关函数的性质,通过特征分解求解污染相位序列,如基于子空间的校正法[3]和最大似然法[4];第三种是基于瞬时频率的估计,如相位梯度法(Phase Gradient Autofocus,PGA)[5];第四种将回波数据进行分段,短时间认为是线性的,如最大熵谱估计法(Maximum Entropy Spectrum Analysis,MESA)[6]和特征分解法[7]。但是使用以上四类方法需要提取标校信号(通常是杂波中能量较大的Bragg峰),其性能依赖于标校信号的完整度,通过带通滤波器提取标校信号时滤波器的带通频率应该尽可能包含不失真的单频信号,同时要尽可能地抑制其他的杂波、噪声和干扰成分,因此带通频率的选择尤为重要。当电离层相位调制的幅度较大时,回波谱正负Bragg峰彼此重叠,给标校信号的提取带来极大的困难。

针对这类情况,文献[8]利用改进的MESA法进行校正,但是当对分段数据估计出的频率误差较大时,该方法性能严重下降;文献[9]和[10]利用级联校正的方法对回波信号进行相位污染校正,基本原理是利用时频分析方法对回波谱进行初步相位补偿,然后再进行精确校正。常用的时频分析方法有短时傅里叶变换法(Short Time Fourier Transform,STFT)和伪维纳分布法(Pseudo Wigner-Vill Distribution,PWVD),但是PWVD对交叉项极为敏感,STFT存在着时频分辨率的矛盾,影响它们的实际应用。目前小波变换是优于傅里叶变换的一种有效的信号处理工具,在时、频域上同时具有良好的局部化特性,文献[11]利用小波变换对多径相位污染的回波信号进行了污染校正。本文针对单模传播长相干积累情况下电离层的大幅度相位调制导致正负Bragg峰重叠的情况,提出一种基于小波变换和模型假设的联合校正方法,将其简称为WTM法。WTM法能够克服PWVD受交叉项敏感以及STFT时频分辨率的矛盾,有效地校正电离层带来的相位污染。

1 信号模型

在点目标前提下,并且只考虑电离层相位污染调制,天波雷达系统的接收信号x(t)可以写成:

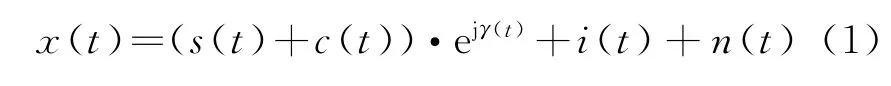
式中,s(t)为目标回波,c(t)为杂波(包括地杂波和海杂波,这里只考虑海杂波)时域响应,γ(t)为电离层信道扰动相位,n(t)为噪声。i(t)包括瞬态干扰和非平稳干扰回波,分别可以通过自适应时域挖除和空域滤波来抑制,这里不考虑。

根据Bragg模型,海杂波分量c(t)可以表示为

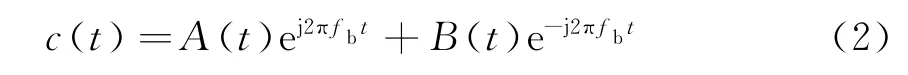
式中,A(t)和B(t)分别为正、负Bragg峰的幅度,fb为Bragg峰频率。电离层带来的相位扰动,导致回波信号频率随机波动,短时间内目标和杂波谱发生频移,在长相干积累时高频回波谱展宽甚至发生分裂。

2 WTM法校正电离层相位污染

2.1 WTM原理描述

在电离层小幅度慢相径污染的情况下,利用现有的补偿算法可以有效地校正回波谱受到的相位污染。但是电离层相位调制的幅度较大时,会使得正负Bragg峰交叠难以准确提取标校信号,现有的补偿算法性能会严重下滑。针对这类情况,采取联合校正以及迭代算法可以有效地校正回波中的污染相位。下面对WTM法进行简述。

2.1.1 小波变换

小波变换是一种有效的信号处理工具,可以应用于对展宽的回波谱进行初步的相位污染校正,其定义式为

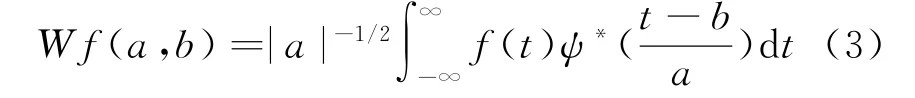
式中,f(t)为平方可积函数,ψ(t)为基本小波或者母小波为小波变换的基函数,a为伸缩因子(也称尺度因子),b为平移因子,式(3)又称为连续小波变换(Continueous Wavelet Transform,CWT)。小波变换伸缩因子a大,频率分辨率高,时间分辨率低;伸缩因子a小,频率分辨率低,时间分辨率高,具有多分辨率的特性,而STFT窗函数的窗口大小不会发生变化,无法同时在两域提高分辨率。

由于时频面内信号的能量几乎分布在瞬时频率附近,对回波信号进行小波变换后,可以在时频域采用谱峰检测的方法进行瞬时频率的估计,文献[10]进行了详细论述。利用估计出的瞬时频率减去fb,进而积分得到污染相位序列进行污染校正,fb可利用式(4)进行计算。

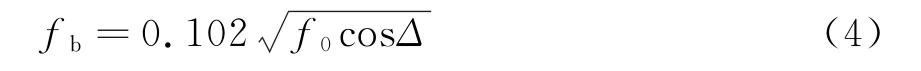
式中,f0为雷达工作频率,Δ为高频信号的入射余角。

2.1.2 自适应标校信号提取

通过2.1.1节的小波变换方法补偿电离层的相位扰动后,展宽的频谱得到一定程度的锐化,正负峰可以初步区分,此时可以提取标校信号进行后续精确的相位污染校正。标校信号的提取通常采用加窗的方式,窗的长度对数据的影响远大于窗的类型[12],同时考虑当电离层扰动较为剧烈时,窗的中心位置可能偏离Bragg峰最大值对应的频率,因此窗中轴位置的选择也影响着标校信号的完整度。由于正、负一阶展宽的Bragg峰一般都在[0,2fb]和[-2fb,0]区间内[13]。这里提出一种基于功率比的滑窗自适应标校信号提取方法,该方法可以选择合适的带通频率进行滤波。提取流程步骤如下:

Step1:计算污染回波X(f)较大Bragg峰对应区间的功率或[-2fb,0]。

Step2:设计一组矩阵滤波器,假设第一个滤波器中心频率为fp=±fb/3,Δf为多普勒分辨率,l为滤波器长度参数,则滤波器对应的截止频率为fp-l·Δf和fp+l·Δf。通过改变滤波器的中心频率fp,使得固定长度的窗(通常采用矩形窗)滑过对应的Bragg峰区间,计算滤出的功率为该组滤波器对应的个数,J k是该组第k个滤波器对应的频率区间。

Step3:计算功率比ξk=P k/G。找到该组滤波器计算出的最大ξ=max{ξ1,ξ2,…,ξm}。

Step4:设置合理的判决门限η,当ξ≥η时,找到ξ对应的第k个滤波器,利用该滤波器取出标校信号,否则增加滤波器长度l回到Step2继续循环。

需要注意的是,基于功率比的滑窗自适应提取方式需要选择合理的判决门限,后续仿真时发现,当η≥90%时提取的标校信号完整度较高。

2.1.3 基于模型的相位污染估计

利用提取的标校信号(假设为正Bragg峰)在时域进行相位污染估计。根据第1节,标校信号z(t)可以表示为

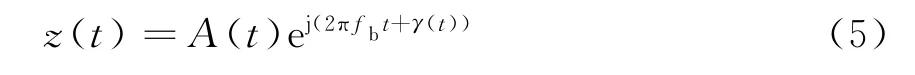
在进行相位污染估计时不考虑幅度污染,认为A(t)是实数,可以忽略幅度变化,此时不影响相位污染校正。则式(5)可以写成如下形式:

将数据写成离散矩阵的形式,则有下式成立:

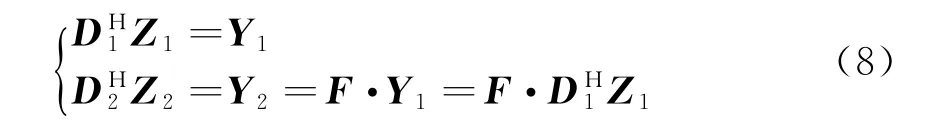
式中:D j(j=1或2)为(N-1)×(N-1)维对角阵;d ij(i=1,2,…,N-1)为D j的对角线元素;D1,D2和Y1,Y2分别对应D,Y的前N-1和后N-1个数据;F为(N-1)×(N-1)维对角阵,其中ωyi表示第i个时刻的污染频率;Z1,Z2分别对应Z的前N-1和后N-1个回波数据,Z j=[z ij],i=1,2,…,N-1。

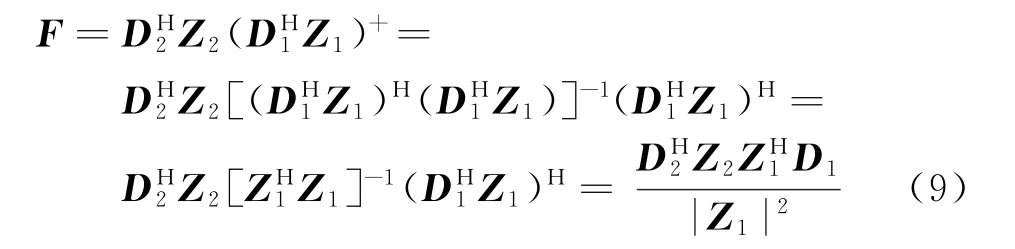
对相位进行估计,可取F=DH2Z2ZH1D1。由于D2,D1可以预先计算,对式(9)进行变换。

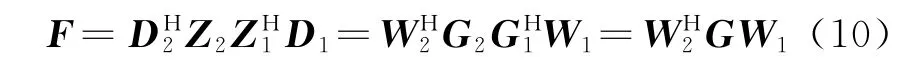
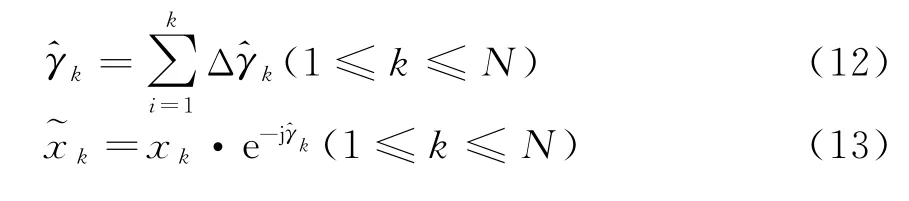
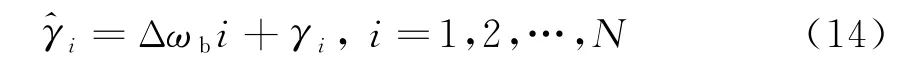
式中,Δωb=2πΔfb·Ts,Δfb为估计的Bragg峰频率与真实值之间的误差,Ts为采样间隔。若…,γN]T,则

根据误差平方和最小求解Δωb:

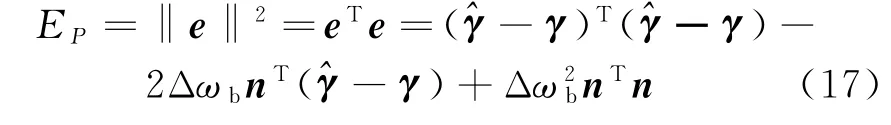
对Δωb求偏导,有下式成立:

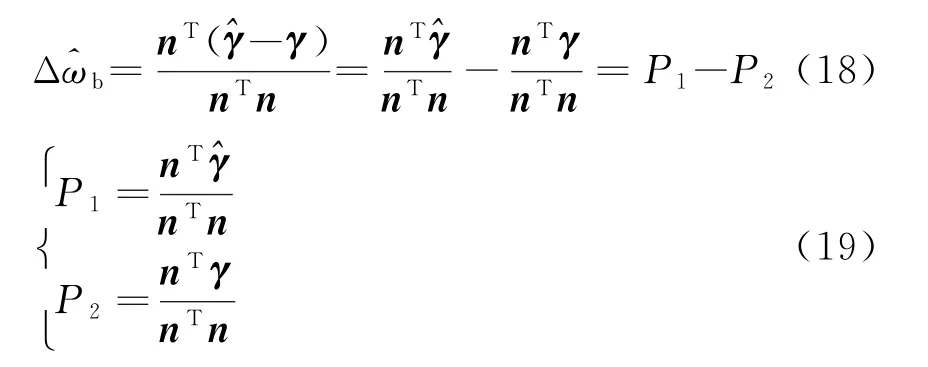
文献[10]利用P1部分对PGA法进行改进,但是仍然会残留斜率为P2的线性误差。残留的线性误差造成频谱偏移,但是不影响目标检测。本文所提WTM法同样利用等式(19)和(20)对回波信号进行污染相位去斜(相当于频谱搬移),可以极大地减小残留线性相位误差。这种去斜的方法同样可以用在2.1.1节小波变换初步相位补偿中。

2.2 WTM法步骤框图

整体校正方法框图如图1所示,可以描述为:

Step1 利用小波变换对某个距离单元一个相干积累时间内的数据进行时频特性分析,利用谱峰搜索出瞬时频率;

Step2 经过Step1得到污染相位,再去除线性斜率,初步补偿回波数据的相位使得正负Bragg峰可以初步区分;

Step3 将校正后的数据进行FFT变换到频域,利用基于功率比的滑窗自适应标校信号提取方法取出标校信号,并进行IFFT变换;

Step4 在时域用基于模型假设的方法进一步精确估计瞬时频率,在去除污染相位斜率后对回波进行校正;

Step5 对校正后的数据进行判断,若频谱仍有展宽需回到Step3进一步迭代校正,否则输出信号。

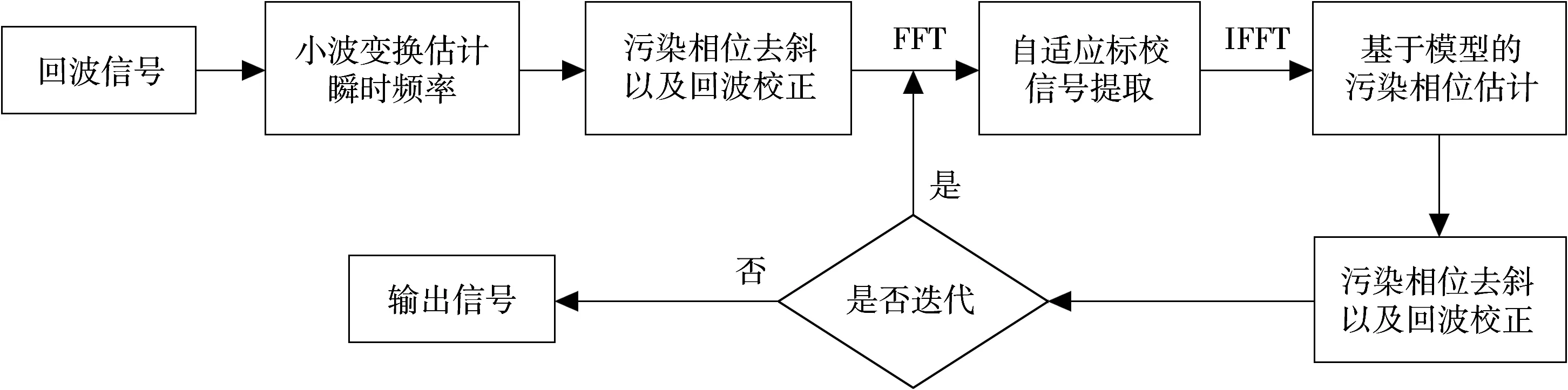
图1 WTM法校正框图

3 仿真分析

为验证 WTM法的有效性,给出计算机仿真结果。仿真时雷达工作频率为15 MHz,脉冲重复频率为5 Hz,相干积累时间内积累512个脉冲,相干积累时间为102.4 s。正、负Bragg峰幅度分别为40和30,杂噪比为25 dB。在-0.53 Hz处有一舰船目标,信噪比为10 dB,对回波数据添加相位污染9 sin(2π·0.04t),图2是受到污染前的回波谱,图3是添加污染后的回波谱。可以看到未受污染的正负Bragg峰清晰可辨,舰船目标也凸现出来;当添加相位污染后回波谱严重展宽,正负Bragg峰发生交叠,舰船目标也被强大的杂波淹没,无法准确地提取标校信号。

图2 污染前回波谱

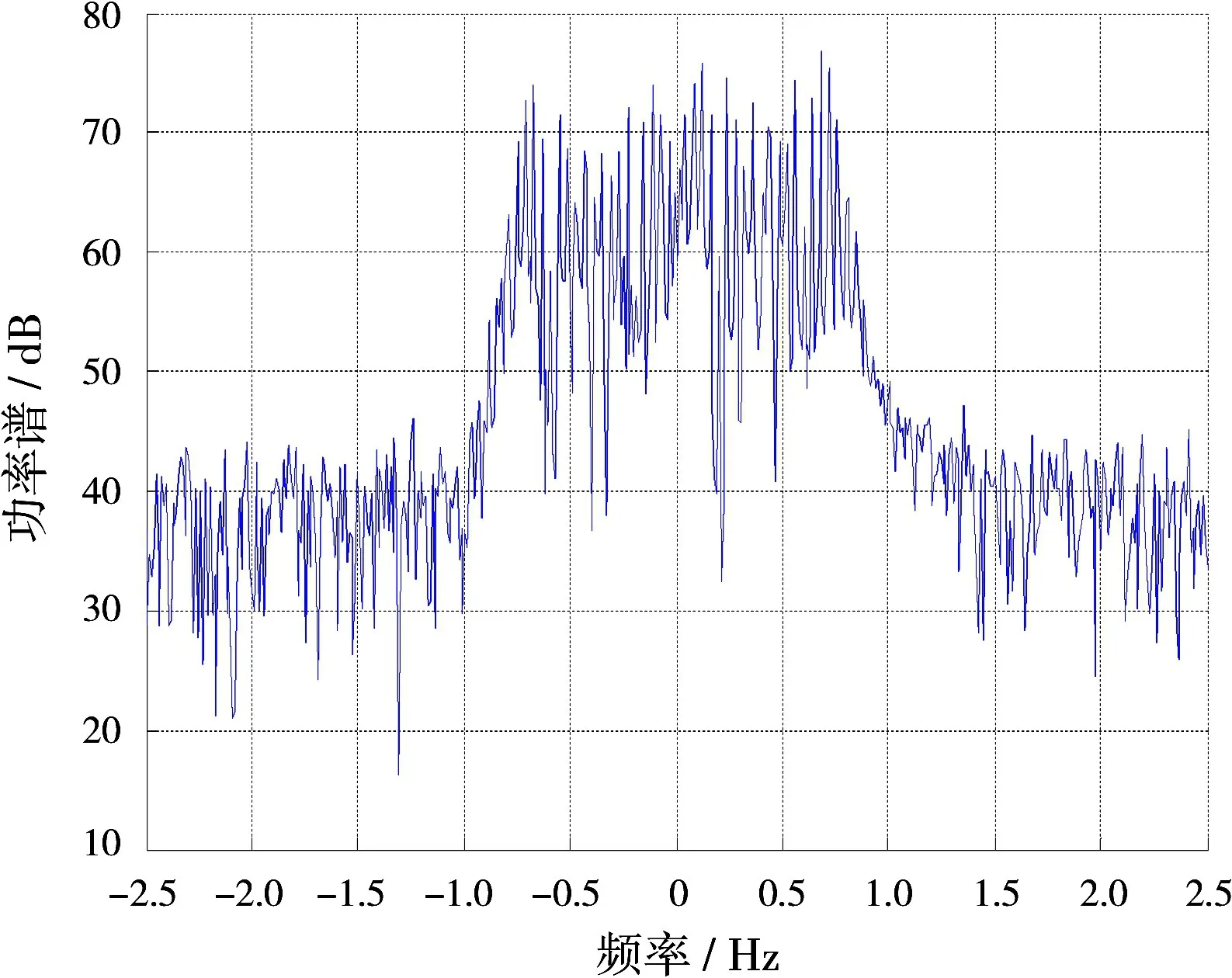
图3 污染后回波谱

利用小波变换初步进行相位污染估计,这里选择CMOR小波对污染后的回波谱进行时频特性分析,需要注意的是文献[11]指出CMOR小波只能显示正频率信号。图4是初步相位校正后的回波谱以及估计出的污染相位,可以看到交叠的Bragg峰已经得到了一定程度的锐化,正负峰可以区分,但是目标仍然被杂波淹没,同时初步估计出的污染相位准确度不高,需要进一步进行相位校正。图5是小波变换和STFT的时频分布,可以看到小波变换时频分辨率高于STFT,主要原因在于小波变换窗长可变,在时、频域均有较高的分辨率,而固定窗长的STFT不能在两域同时提高分辨率。

对已经在一定程度锐化可分的回波数据进行标校信号的自适应提取,在以后的校正过程中均采用基于功率比的滑窗自适应提取方式。利用2.1.3节的方法对回波信号进行相位污染校正,校正后的频谱如图6所示,回波谱正负Bragg峰进一步锐化、变窄且目标清晰可见。图7是利用WTM法估计出的相位污染,与添加的污染较好地吻合。图8是没有采用等式(18)和(20)对回波信号进行相位污染去斜的结果,相比图7可见,未去斜前估计出的相位污染明显存在线性误差,去斜后显著降低,但是依然会有一个微小的线性斜率,此时并不影响目标的检测。另外需要说明的是,这里只采用了一次WTM法进行校正,如果校正后的回波谱仍有所展宽,可采用迭代的方法进一步对相位进行补偿。图9是利用改进MESA法校正后的回波谱,目标虽然显露出来,但是回波谱仍有一定程度的展宽,相比可见,WTM法校正精度更高。

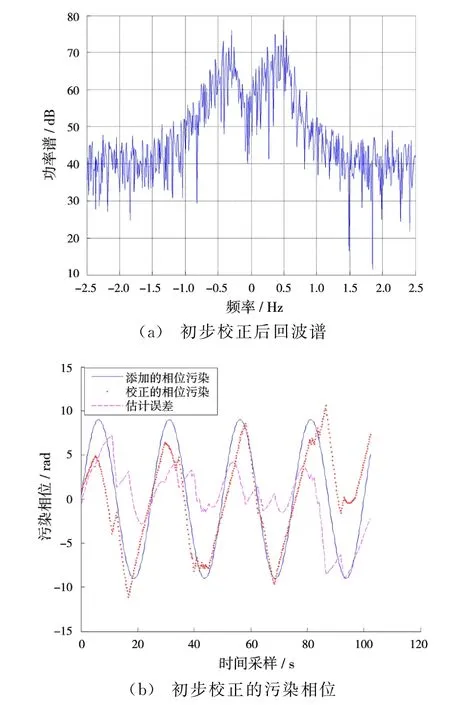
图4 小波变换初步相位校正

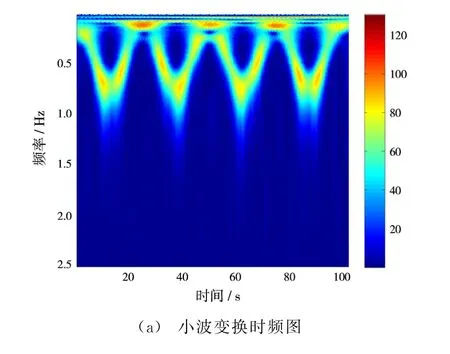
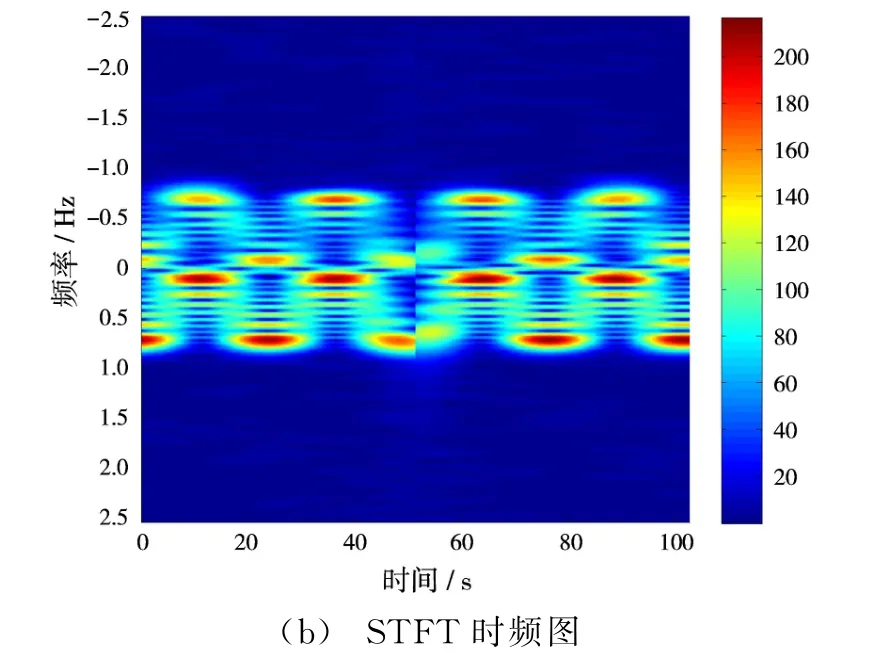
图5 小波变换和STFT时频图

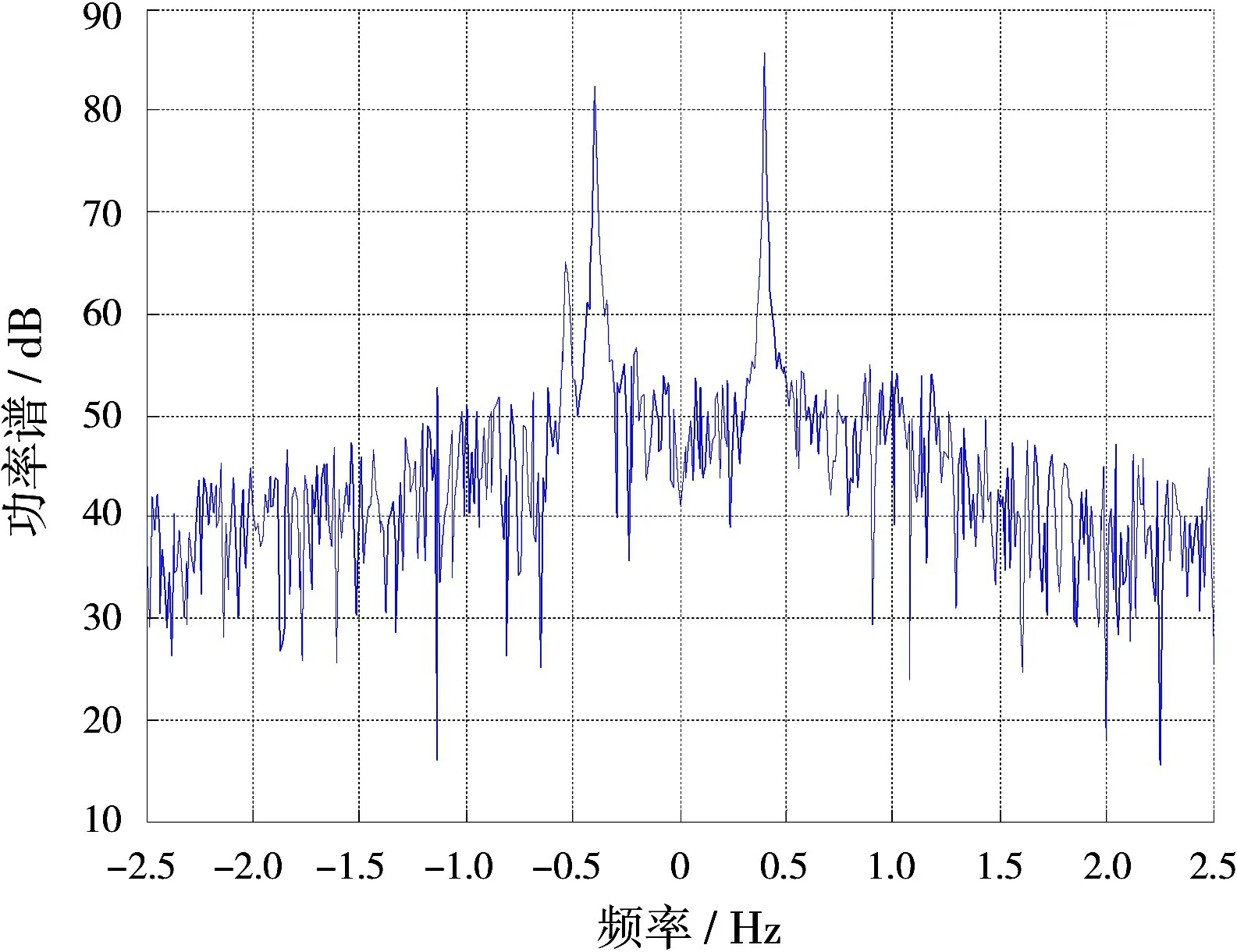
图6 WTM校正后回波谱

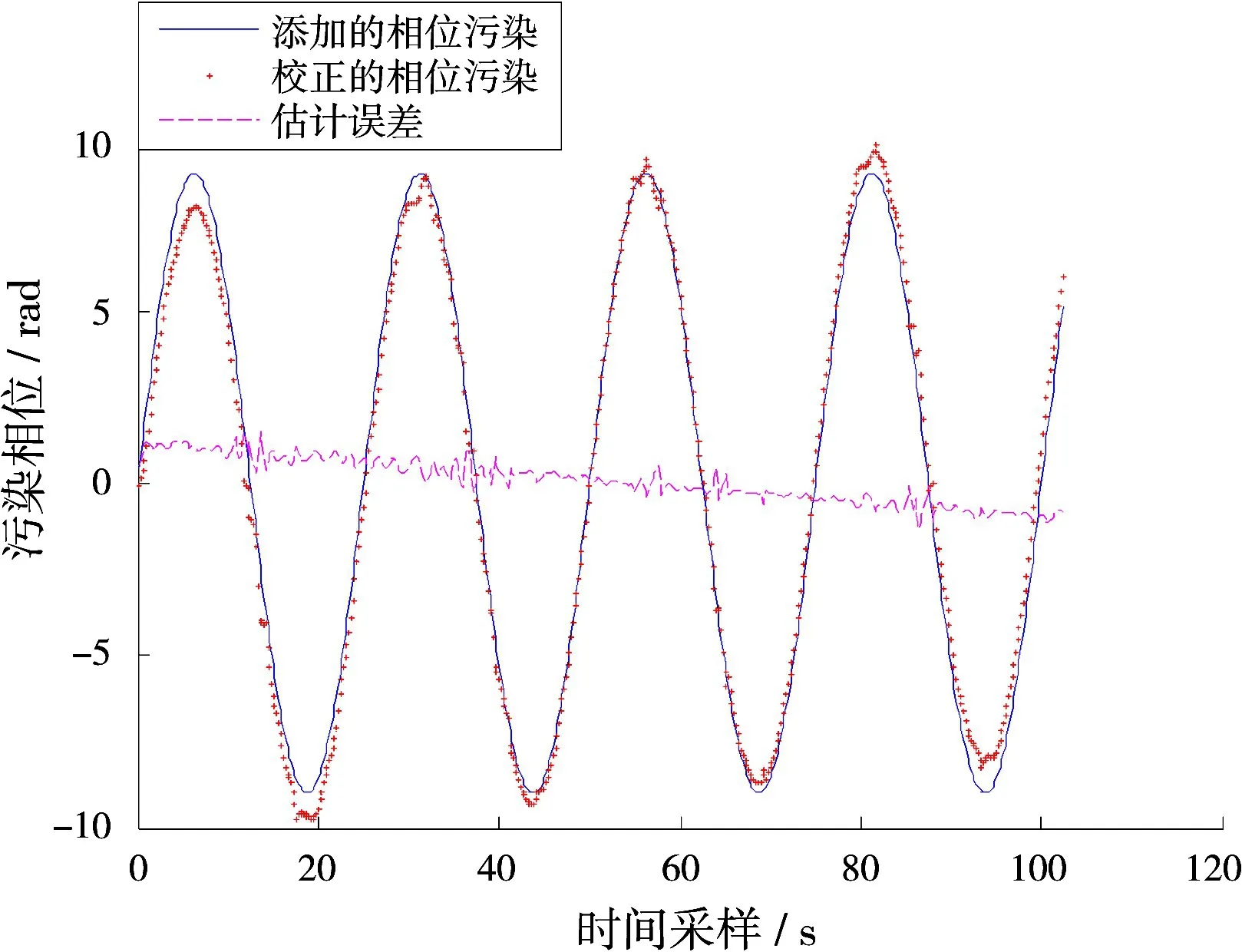
图7 WTM法估计出的污染相位

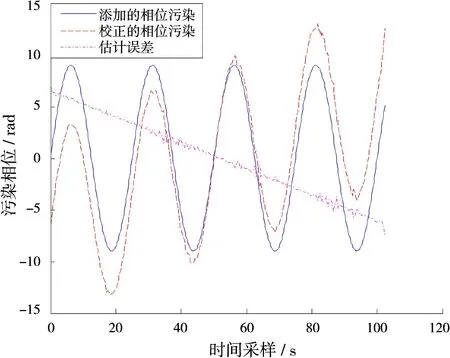
图8 WTM法未去斜估计出的污染相位

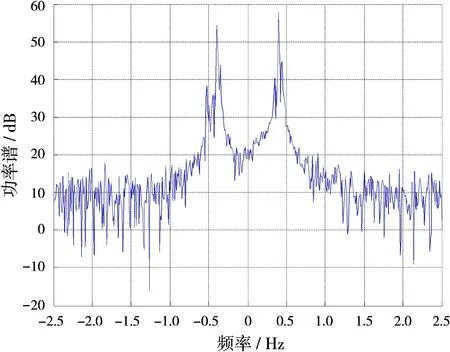
图9 改进MESA法校正后回波谱

4 结束语

电离层相位污染是制约天波超视距雷达发展的关键问题之一,对电离层污染校正的效果直接影响着雷达的探测性能。由于电离层的非平稳和时变特性,回波信号受到电离层扰动,海面慢速目标淹没在展宽的杂波中。本文针对单模传播长相干积累情况下电离层大幅度相位污染导致的频谱展宽、正负Bragg重叠情况提出了一种联合小波变换和基于模型假设的WTM校正方法。首先利用小波变换对交叠的频谱进行频率估计,初步补偿污染相位,针对已经初步锐化可分的频谱利用基于功率比的滑窗自适应方法来提取杂波的强Bragg峰作为标校信号,在时域根据假设的模型对回波数据进一步进行相位补偿,得到无污染的高频回波谱,同时原本因为展宽而掩盖的目标信号也清晰可见,最后对残留的微小相位线性误差进行了分析。仿真实验说明了 WTM方法的有效性,性能优于已提出的改进MESA法。

需要说明的是,目前对电离层相位污染的研究主要集中在慢变相位的估计上,如何有效地补偿快变相位失真需要进一步研究。同时针对电离层分层结构带来的多径效应,不仅仅要从接收端信号处理加以校正,发射端的波形设计优化同样重要,文献[14]利用MIMO体制从发射端对天波雷达波形进行优化设计,利用分时波束空间MIMO天波雷达进行多径抑制取得了较好的效果。另外,文中采用较为纯净的天波雷达模拟数据来分析、验证所提WTM法的性能,尚有待进一步开展实际验证。

[1]胡进峰,艾慧,李万阁,等.基于匹配傅里叶变换的相位解污染算法[J].雷达科学与技术,2015,13(3):291-295.

[2]LU K,WANG J,LIU X.A Piecewise Parametric Method Based on Polynomial Phase Model to Com-pensate Ionospheric Phase Contamination[C]∥IEEE International Conference on Acoustics,Speech,and Signal Processing,New York:IEEE,2003:405-408.

[3]BO C,GU H,SU W,et al.Ionosphere Phase Decontamination Method Based on Subspace in Sky-Wave OTHR[J].Electronics Letters,2014,50(24):1874-1875.

[4]罗欢,陈建文,鲍拯.同时校正电离层幅度和相位污染的MLE方法[J].华中科技大学学报(自然科学版),2013,41(9):17-21.

[5]邢孟道,保铮.电离层电波传播相位污染校正[J].电波科学学报,2002,17(2):129-133.

[6]BOURDILLON A,GAUTHIER F,PARENT J.Use of Maximum Entropy Spectral Analysis to Improve Ship Detection by Over-the-Horizon Radar[J].Radio Science,1987,22(2):313-320.

[7]ANDERSON S J,ABRAMOVICH Y I.A Unified Approach to Detection Classification,and Correction of Ionospheric Distortion in HF Sky Wave Radar Systems[J].Radio Science,1998,33(4):1055-1067.

[8]李钢,杨仕文,刘颜回,等.天波超视距雷达电离层大幅度相位污染校正算法研究[J].宇航学报,2008,29(2):670-674.

[9]LIU Y,NIE Z,ZHAO Z,et al.A Cascaded Correction Method to Reduce the Contamination of Ionospheric Frequency Modulation for HF Skywave Radars[C]∥Antennas and Propagation Society International Symposium,Charleston,SC:IEEE,2009:1-4.

[10]罗欢,陈建文,鲍拯.一种天波超视距雷达电离层相位污染联合校正方法[J].电子与信息学报,2013,35(12):2829-2835.

[11]刘清艳,杨强,姜维.基于CMOR小波的雷达信号解相位污染方法[J].微计算机信息(测控自动化),2009,25(4-1):305-307.

[12]LIU Y,NIE Z,ZHAO Z.A Method to Adaptively Compensate for Ionospheric Layer Movement in HF Sky Wave Radar Systems[J].Journal of University of Electronic Science and Technology of China,2008,37(3):335-338.

[13]PARENT J,BOURDILLON A.A Method to Correct HF Skywave Backscattered Signals for Ionospheric Frequency Modulation[J].IEEE Trans on Antennas and Propagation,1988,36(1):127-135.

[14]赵志国,陈建文,鲍拯.分时波束空间MIMO天波雷达发射ADBF方法[J].华中科技大学学报(自然科学版),2013,41(2):64-69.