一种用于高频雷达探测性能评估的方法

(哈尔滨工业大学(威海)信息与电气工程学院,山东威海264209)

0 引言

高频地波雷达利用垂直极化电磁波沿海面绕射传播衰减较小的机理,实现地平面以下的海面和空中目标的超视距探测[1],并具有反隐身、反超低空突防、抗反辐射导弹等能力[2]。探测性能作为雷达主要的战术指标,直接体现了雷达完成其战术任务的能力。因此对探测性能作出科学合理的评估,能够为雷达的布阵、指挥系统、情报系统等提供准确有效的资料[3]。同时,对地波雷达探测性能指标体系的建立和评估方法的研究,可为雷达系统寿命周期的各个阶段提供决策依据。高频地波雷达作为一个复杂而庞大的系统,影响其探测性能的因素众多而庞杂,既有定量的也有定性的,这使得对高频地波雷达的探测性能评估相对于常规雷达更有难度。为了合理而全面地评估高频地波雷达的探测性能,必须对影响其探测效果的各种因素进行综合分析和评价。因此,对高频地波雷达建立起一套合理而科学的探测性能评估指标体系,并选取切实有效的评估方法,具有重要的实际应用意义。

随着高频地波雷达系统的发展,通过借鉴其他体制雷达的评估手段[4-5]并受其他领域的启发,其评估手段也经历了一个从无到有的过程。目前,国内外对高频地波雷达探测性能的评估手段多以专家打分为主[6],主观性较强,且指标体系多在静态条件下建立,对外部环境和系统的动态变化不甚敏感。文献[7]采用性能参数法和解析法相结合的方法,通过具体量化系统性能指标对高频地波雷达进行评估,但其指标体系不够全面,而且对用户的专业水平要求较高。文献[8]借鉴层次分析法,建立了高频地波雷达作战效能评估的层次结构,并给出了理论计算方法,但很大程度上仍依赖专家打分,主观因素较多,同时缺乏实测数据支持。文献[9]首次系统地介绍了高频地波雷达性能评估的准则,提出自上而下准则,每一层采用单一性能指标进行评判,并首次将模糊推理的概念引入到地波雷达性能评估中,从而使用户对雷达性能有较为直观的认识,但其只是进行了定量分析,并没有与定性分析相结合。

本文首先建立了完整的高频地波雷达探测性能评估指标体系,然后提出了基于遗传算法[10]的层次分析法(Genetic Algorithms-Analytic Hierarchy Process,GA-AHP)对地波雷达的探测性能进行评估,提高了算法的稳健性和评估结果的精确度。不同于以往的研究大多是理论探讨,本文将该评估方法与哈工大威海雷达站实测数据相结合,确定相应的参数指标,检验了模型的正确性和准确性,对高频地波雷达的研发、技术改进以及探测性能评估具有很高的实际指导价值。

1 基于AHP的HFSWR探测性能评估方法

1.1 建立层次分析结构模型

层次分析法[11](Analytic Hierarchy Process,AHP)将复杂的决策问题分解为目标、准则、方案三层。影响高频地波雷达探测性能评估指标可分为三部分:环境及目标特性评估指标、探测性能技术指标以及探测性能战术指标。其中,环境及目标特性评估指标包括海杂波[12]、雷达散射截面积[13]等;探测性能技术指标包括发射机功率、雷达工作频率等;探测性能战术指标包括距离分辨率、速度分辨率等。高频地波雷达系统的3层探测性能评估体系如图1所示,其中A代表最高层、B代表中间层、C代表最底层。

图1 高频地波雷达探测性能评估层次分析结构图

层次分析结构建立后,对除最高层外的每一层中的元素建立相对于上一层的判断矩阵。同一层的各元素之间的相互关系是专家基于上一层准则对它们相互比较得出,构造出的判断矩阵为

式中,a ij为某一层中因素i相对于因素j的重要性,采用1～9标度法[14]量化获得。

如果矩阵A中的元素满足一致性条件:

则称矩阵A为一致性判断矩阵。根据一致性判断矩阵的特性,则

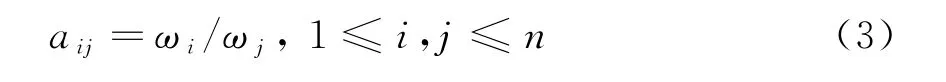
进一步得到

式中,W为权重向量,W=(ω1,ω2,…,ωn)T。由式(4)得出,判断矩阵A的最大特征根所对应的特征向量即为该层指标相对于上一层的权重向量。

1.2 一致性检验及总层次排序

当n阶判断矩阵A满足完全一致性条件时,其特征值满足:

而当判断矩阵A不满足完全一致性条件时,有

由式(5)、(6)对比可知,判断矩阵偏离完全一致性程度的方法如下:

1)计算一致性指标CI(Consistence Index)

2)已知判断矩阵的阶数n,根据表1得到平均随机一致性指标RI[15](Random Index)。

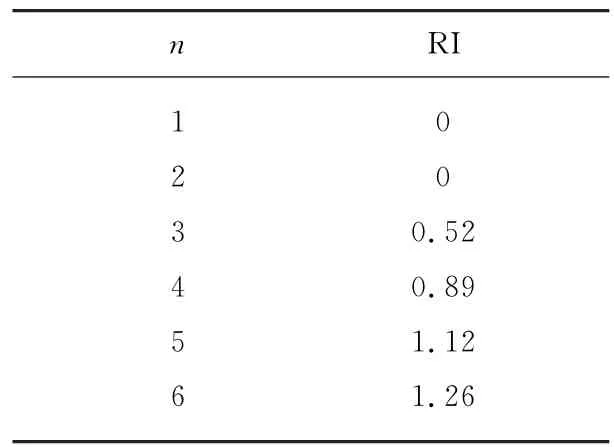
表1 RI与判断矩阵阶数n的关系

3)定义判断矩阵的一致性比例CR(Consistency Ratio)为

当判断矩阵的阶数低于二阶时,其判断矩阵满足完全一致性,而当阶数超过二阶时,定义当CR＜0.1时,对应的判断矩阵具有满意的一致性,否则需对判断矩阵进行修正。

对决策问题的分析,所需的是方案层指标对目标层的影响。因此,在单层次排序的基础上,仍需对各层指标的权重进行合成,以获得方案层对目标层影响的权重。

设第k层(非最顶层)包含n k个指标,且相对于上一层第j个指标的权重向量为

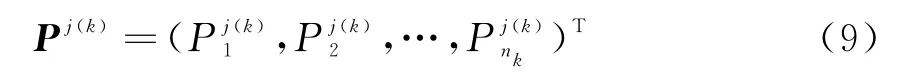
第k-1层的n k-1个指标相对于顶层的合成权重向量为

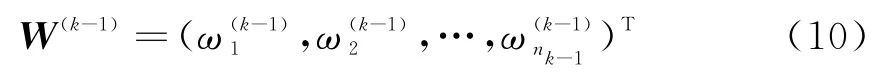
记第k层n k个指标相对于其上一层各指标的权重矩阵为

2 基于遗传算法的改进层次分析评估法

在已知某一层判断矩阵A=(a ij)n×n的基础上,若判断矩阵A满足式(3),此时判断矩阵A具有完全一致性,因此有如下关系成立:

进一步得

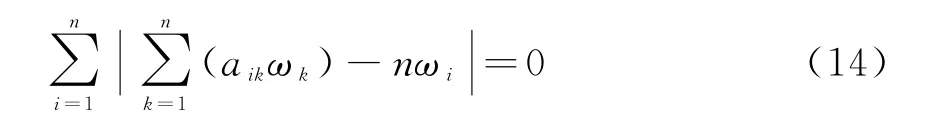
判断矩阵的一致性程度越高,式(14)左端的值也就越小。因此,在层次分析法中,对单层指标直接的权重向量求解及一致性检验问题均可总结为下列非线性函数的优化问题:

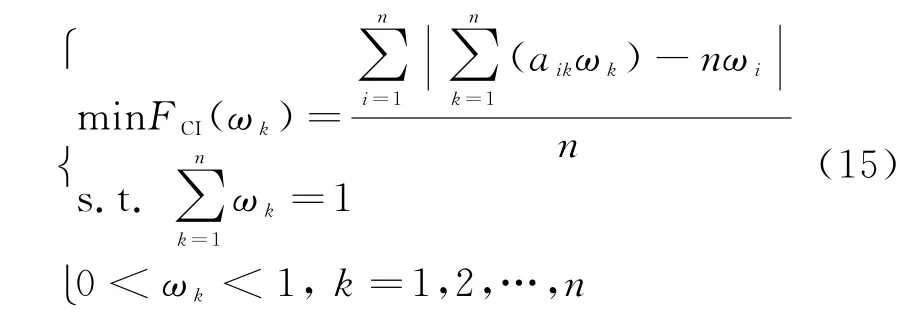
式中,FCI(ωk)为一致性指标函数,权值ωk为待优化变量。根据约束条件可以证明,此全局最小值具有唯一性。

通过遗传算法对式(15)的函数模型进行最小值搜索,当一致性检验指标FCI(ωk)小于0.10时,认为判断矩阵具有满意的一致性,否则继续进行迭代。

3 探测性能评估方法仿真

根据哈工大威海高频地波雷达的实际探测性能评估参数,对各层中指标之间的关系进行量化构造判断矩阵 ,如表2～4所示。

表2 A～B和B3～C判断矩阵

表3 B1～C判断矩阵

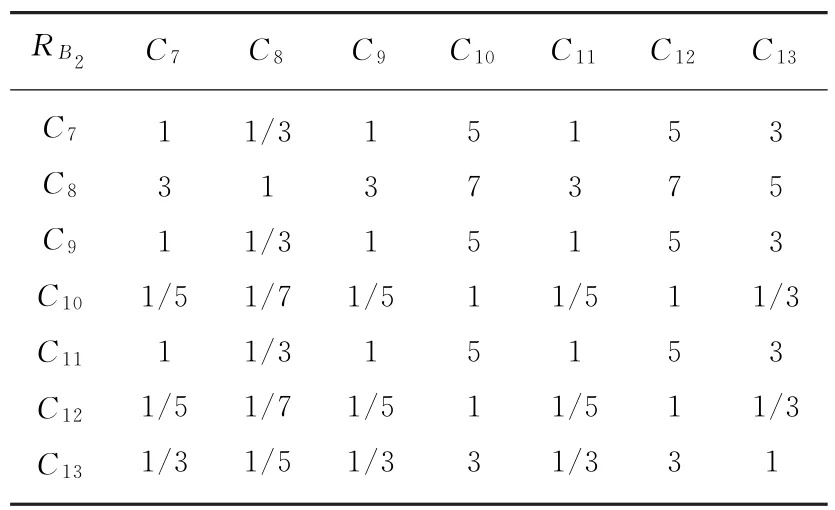
表4 B2～C判断矩阵

根据表2～4给出的各层判断矩阵,分别采用传统层次分析法和基于遗传算法的改进层次分析评估方法进行仿真分析。设定初始群体大小为80,交叉概率pc和变异概率pm分别为0.8和0.01,进行100次迭代,对各层判断矩阵进行仿真分析,其输出的最优适应值曲线如图2所示,对应的合成权重如图3所示。从图2可以看出,随着迭代次数增加,适应值满足收敛且满足一致性检验。

由图3可知,采用上述两种评估方法,其分机指标对于探测性能影响的合成权重大致相同,但使用AHP方法求解出的权值向量比较粗糙。尽管它可以在一定程度上反应各指标对高频雷达探测性能的影响,但是这些指标的相对关系并不明确。虽然GA-AHP求解的权值向量与AHP方法趋势大致相同,但是GA-AHP求解的精度更高,这具体表现在某些指标对高频雷达探测性能影响的合成权重上,即通过AHP方法求解的权值中,1,2和4项指标,3和5项指标,9和11项指标,14,15和16项指标的权值相同,表明它们对系统探测性能的影响是相同的,但是这与高频雷达的实际情况不符。而通过GA-AHP求解的权值向量中上述权值都有明确的相对大小关系且符合高频雷达的实际情况,因此它能精确地区分出各分机指标的相对重要性与绝对重要性,从而能够更加准确地把握高频雷达探测性能与各分机指标之间的逻辑关系。

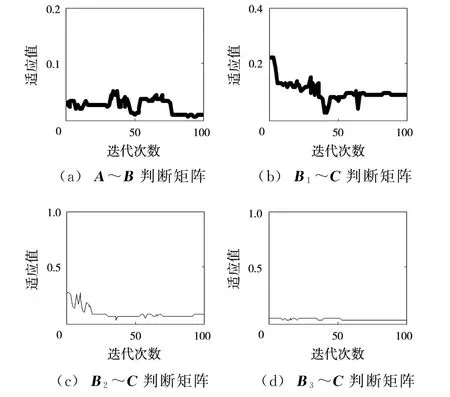
图2 最优适应值曲线

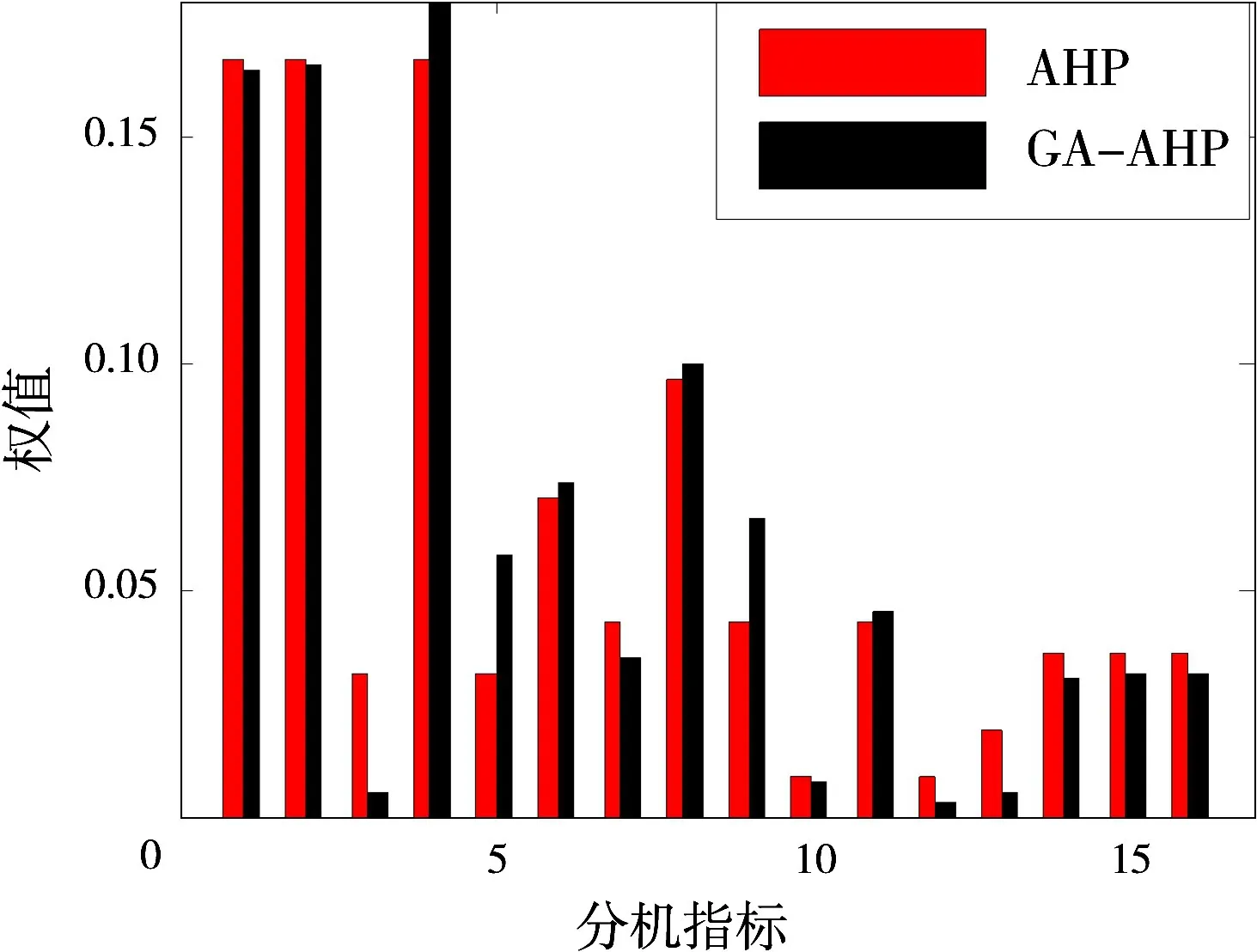
图3 分机指标对系统探测性能影响的合成权重

4 结束语

本文首先构建了HFSWR探测性能评估的层次分析结构模型,然后选用特征值向量法定量给出了分机指标对探测性能的影响大小。该方法存在的不足是:一方面,判断矩阵的权重排序与一致性检验是各自独立进行的,在判断矩阵确定的情况下,其一致性检验指标的优劣在进行过权重排序及一致性检验后才能得知,是一种“被动”方法;另一方面,从优化的角度分析,特征值向量法属于求解判断矩阵权重排序的近似算法,其不可避免地带来计算结果的不精确。针对传统层次分析法评估的缺陷,利用遗传算法处理非线性问题的优点,将遗传算法与层次分析法有效结合,提出了GA-AHP。它克服了传统方法中判断矩阵的权重向量获取与一致性检验独立进行的缺点 ,将权重排序与一致性检验合二为一,归纳为非线性优化问题,从而更好地解决判断矩阵的一致性问题,也提高了评估算法的稳健性和评估结果的精确性和可信度。试验表明该评估方法能够有效地提高评估结果的精度,具有一定的实际应用价值。

[1]陈文涛,马子龙,周必全.高频地波雷达系统优化控制的研究与建模[J].雷达科学与技术,2014,12(1):13-19.CHEN Wen-tao,MA Zi-long,ZHOU Bi-quan.Research and Modeling of Performance Evaluation and Optimizing Control in High Frequency Surface Wave Radar[J].Radar Science and Technology,2014,12(1):13-19.(in Chinese)

[2]张雅斌.高频地波雷达干扰与海杂波信号处理研究[D].西安:西安电子科技大学,2010:1-20.

[3]吴少鹏.基于域层化的雷达指标体系结构及规范方法探讨[J].雷达与对抗,2012,32(1):1-3.

[4]TURLEY M D E,TYLER M A.A Technique for Estimating the Detection Performance of a Skywave Over-the-Horizon Radar[C]∥International Radar Conference,Bordeaux:IEEE,2009:1-5.

[5]HOLDSWORTH D A.An Over-the-Horizon Radar Performance Assessment Module for Use in Cognitive Radar[C]∥IET International Conference on Radar Systems(Radar 2012),Glasgow,UK:IET,2012:1-6.

[6]MARESCA S,HORSTMANN J,GRASSO R,et al.Performance Assessment of HF-Radar Ship Detection[C]∥Proceedings International Radar Symposium(IRS),Leipzig:IEEE,2011:131-136.

[7]孙长国,栾厚斌,席泽敏.地波超视距雷达作战效能评估模型[J].舰船科学技术,2003,25(5):37-39.

[8]郭万海,张淑芳,闫国玉,等.高频地波雷达作战效能评估方法研究[J].现代防御技术,2008,36(2):133-137.

[9]KEWLEY D J,DALL I W.Performance Assessment Criteria for OTH Radar[C]∥International Radar Conference,Brighton:IET,1992:1-4.

[10]ALBAYRAK M,ALLAHVERDI N.Development a New Mutation Operator to Solve the Traveling Salesman Problem by Aid of Genetic Algorithms[J].Expert Systems with Applications,2011,38(3):1313-1320.

[11]SAATY T L.The Analytic Hierarchy Process[M].New York:McGraw-Hill,1980.

[12]CROMBIE D D.Doppler Spectrum of Sea Echo at 13.56 Mc/s[J].Nature,1955,175(4459):681-682.

[13]张文敏.高频段电离层特性及雷达综合频率选择方法研究[D].哈尔滨:哈尔滨工业大学电子与信息工程学院,2011:20-38.

[14]韩培骏.红外导引系统抗干扰性能评估准则与方法研究[D].南京:南京航空航天大学自动化学院,2012:27-36.

[15]徐泽水.判断矩阵一致性修正的新方法[J].系统工程理论与实践,2000(4):86-89.