一种新的双基地MIMO雷达杂波模拟方法∗

(电子科技大学电子工程学院,四川成都611731)

0 引言

现代战场环境日益复杂,为了实现对多样化目标进行探测和跟踪,提高雷达的“四抗”能力,人们不断地探索新的技术途径[1]。MIMO技术的使用给雷达系统的性能突破带来了新的契机[2],特别是与双/多基地雷达体制完美地结合起来,弥补彼此的不足,在低空探测、反隐身、抗反辐射导弹等诸多方面表现出较大的优势[3-4]。

受强地杂波影响,雷达对地面低空目标的探测性能受到很大限制。国内外对单基地雷达杂波建模的研究已较成熟,但对双基地MIMO雷达的杂波特性却少有研究。双基地MIMO雷达发射相互正交的信号,同一杂波单元的回波信号形式不同,不同杂波单元回波信号形式也不同,而且等距离环为椭圆,在椭圆圆环上积分来计算杂波单元面积,求解杂波单元相对于雷达基地的角度,计算量很大。文献[5]提出了一种将杂波单元近似地看作矩形的计算杂波单元面积的方法,但只在远场适用;文献[6]提出了一种将地面划分为接收角、发射角、距离都不可分辨的杂波散射单元的方法,通过固定发射角变化量,由距离分辨率约束求取接收角变化量。但随着接收角的增大,为了满足距离分辨率约束,将导致接收角变化量变得很小,得到很多的杂波单元,运算量极大,不利于杂波仿真,并且在远场处无论接收角变化量多小也无法满足距离分辨率。

本文提出一种新的杂波单元划分方法及预存储的处理技术,在接收角和发射角扫描区域,将地面划分为接收角、发射角都不可分辨的杂波单元,再由满足距离分辨率的等距离环划分得到所需的杂波单元;并通过预先划分,采用结构体形式存储数据的方法提高杂波仿真效率。本文的研究内容是研究双基地MIMO雷达在杂波背景下检测性能的前提,具有一定的实用价值。

1 杂波信号模型

双基地MIMO雷达的发射通道数为M,接收通道数为N,则发射基带信号为

基带信号相互正交,则接收信号为

将杂波单元看作静止的点目标,则其回波信号可表示为

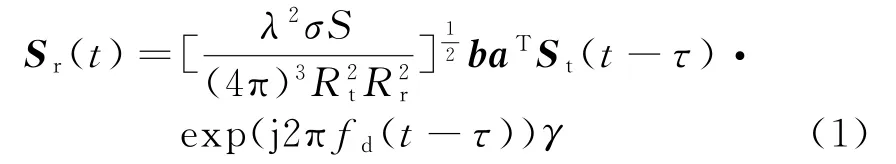
单基相控阵雷达通道间发射信号一致:St1(t)=St2(t)=…=StM(t)=S(t);且等距离环上不同杂波单元回波的信号形式也相同,仅存在多普勒以及阵元间距引起的相位差,并且这种差异的统计特性服从特定的几种分布,可以通过统计建模的方法模拟总的杂波回波。

双基地MIMO雷达发射正交信号,在空间不能叠加,不同杂波单元回波信号形式不同,而且双基地雷达等距离环为椭圆,难以通过积分的方式计算杂波,所以必须将地面划分为发射角、接收角、距离都不可分辨的杂波单元,分别计算每个杂波单元的回波信号,然后通过矢量求和的方法得到总的杂波信号。

2 杂波单元划分

双基地雷达的左视区和右视区是对称的,所以只需研究左视区即可。如图1所示,建立直角坐标系,双基地基线在x轴上,基线距离为L;θt为发射角,Δθt为发射角变化量,θr为接收角,Δθr为接收角变化量。

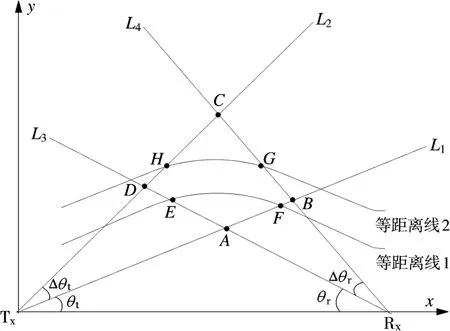
图1 双基地雷达杂波单元划分

发射阵列的半功率波束宽度为

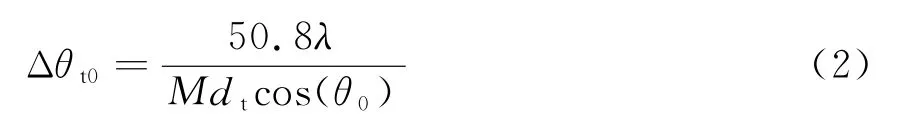
式中,θ0为发射波束指向,λ为波长,M为发射阵元数,dt为发射阵元间距。为了保证杂波仿真的精度,在此发射角变化量保守地取:

同理接收角变化量取为

式中,N为接收阵元数,dr为接收阵元间距。最后再由满足距离分辨率的等距离环完成划分。

图1中直线L1,L2,L3,L4的方程为

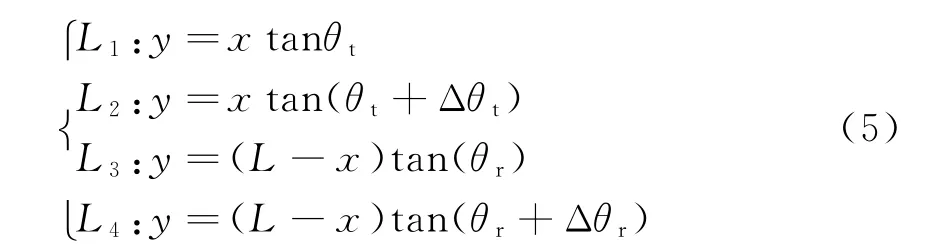
式中,L为基线距离,由4条直线方程求得A,B,C,D四点坐标为

等距离环距离间隔为

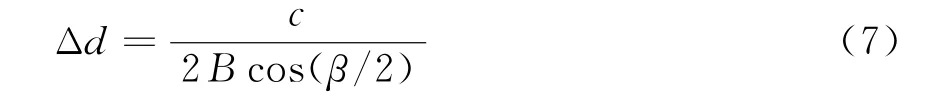
式中,c为光速,B为信号带宽,β为双基地角,β=π-θt-θr。易知A点到发射和接收基地的距离和dA最小,C点最大为dC,等距离环从A开始,C以内距离C最近的等距离环结束,等距离环的距离和:

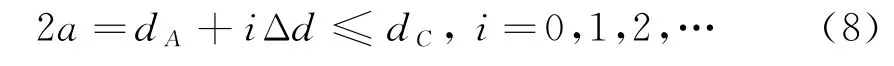
则椭圆方程为

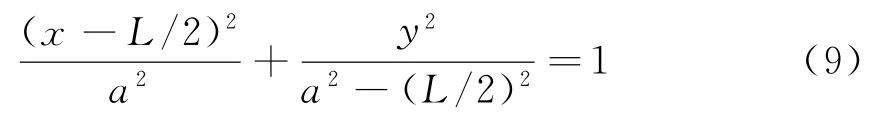
分为:1)A在椭圆内,B,C,D在椭圆外;2)A,B在椭圆内,C,D在椭圆外;3)A,D在椭圆内,B,C在椭圆外;4)A,B,D在椭圆内,C在椭圆外四种情况依次求出每个等距离环与四边形ABCD的交点坐标。将所得的杂波单元近似地看作四边形EFGH,假设四点坐标为E(xe,ye)、F(xf,yf)、G(xg,yg)、H(xh,yh), 则 四 边 形EFGH面积为

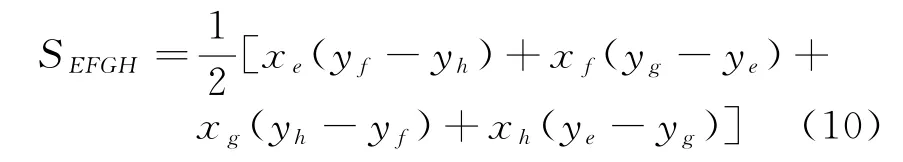
求取四边形EFGH的重心Z[6],进而得到杂波单元重心Z到收、发基地的距离Rr,Rt。

3 划分预存储技术

在每次杂波仿真过程中存在大量重复性计算,一般情况下,杂波单元的划分及相关参数都是不变的,因此可以提前计算出这些参数并存储为结构体的形式以供调用,进一步提高了仿真效率。

实际上,双基地雷达发射站和接收站的阵元配置,即阵元个数和间距通常是不变;基线距离也是不变的。对于每个杂波单元,只要发射信号的波长和带宽不变,则每次划分出的杂波单元也是不变的,具有相同的杂波单元面积S,散射系数σ,发射角θtgtt,接收角θtgtr以及距离发射站和接收站的距离Rt,Rr。因此仿真杂波时不必每次都对杂波单元进行划分,可以提前将所需参数:S,σ,Rt,Rr以不同的发射角θtgtt和接收角θtgtr为单元保存为结构体的形式。其中S存储了四边形ABCD被等距离环划分后的各杂波单元的面积;Rr,Rt是对应的各杂波单元与收、发站的距离;σ由双基地角决定,经过大量实测数据统计分析,其值如图2所示。

图2 平面外散射系数

仿真杂波时,只需要调取这些参数,由式(1)求得各个杂波单元的回波信号,通过矢量求和的方法得到总的杂波信号。同时,杂波单元划分预存储技术也方便了并行计算的编程,为更快地仿真杂波提供了操作空间。

4 仿真结果及分析

假设双基地MIMO雷达收、发阵列为平行于基线放置的面阵,阵元数为16×16,阵元间距dt=dr=λ/2;发射阵划分为1×16的子阵,每个子阵阵元为16×1,发射通道数M=16;接收阵划分为4×4的子阵,每个子阵阵元为4×4,接收通道数N=16;基线长度为30 km;杂波地形为有房屋和树林的郊区,雷达工作在C波段,频率为5 300 MHz,雷达周期T=1 ms;发射功率为1 W,各发射阵元发射相互正交的步进频线性调频信号,频率间隔ΔB=0.5 MHz,带宽B=8 MHz,发射脉冲数为32,脉宽Tp=409.6μs。发射波束和接收波束指向θt=θr=45°,俯仰角φt=φr=5°。

按文献[6]方法划分出杂波单元,在不考虑回波信号幅度的情况下,在距离维画出各杂波单元双基地距离和R=Rr+Rt,即杂波脉压后在距离维出现的位置,如图3所示。可以看出,随着双基地距离和的增大,杂波单元在距离维不再连续,不满足距离分辨率。新的杂波模拟方法得到的杂波单元满足距离分辨率要求,如图4所示。划分杂波单元数n=685 764,采用划分预存储技术,在仿真杂波时避免了2n次解方程计算,以及22n次乘法计算。仿真时间从改进前的246 672 s提升为28 559 s,运用GPU(Graphic Processing Unit)的大规模并行计算能力可以更进一步减少仿真时间。

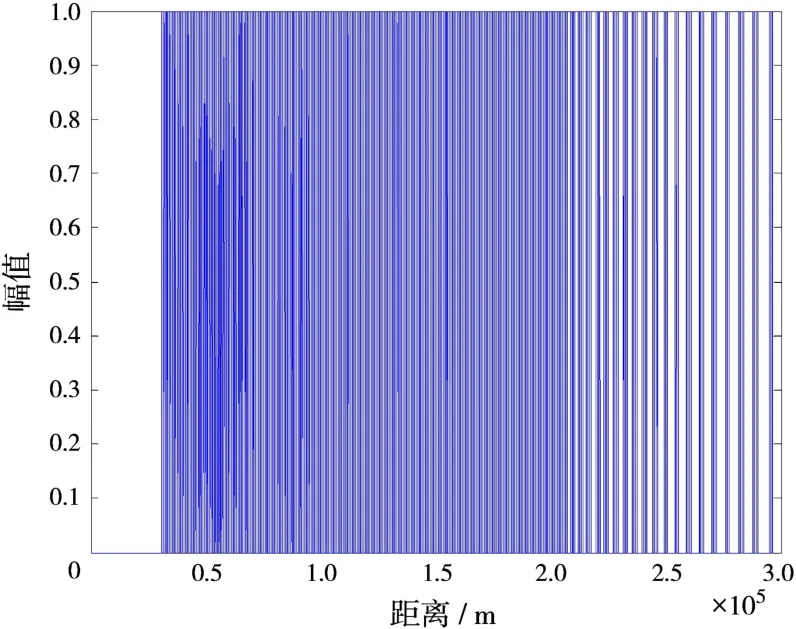
图3 原划分方法杂波单元距离分布

图4 新划分方法杂波单元距离分布

由于杂波单元实际是带圆弧边的不规则图形,且忽略了部分小面积区域,所以杂波单元面积S的计算存在误差,如图5所示。从图5可以看出,误差在1.5%以内,是可以接受的。

图5 不同角度的杂波单元面积误差

图6为双基地MIMO雷达地杂波谱,双基地基线距离为30 km,所以在0～30 km范围内没有杂波;在基线距离附近杂波信号幅度较大,是因为距离较近且散射系数也较大。图7为阵列天线的方向图,受方向图调制、散射系数、相关性系数、匹配滤波旁瓣等多因素影响,不同距离单元的杂波信号幅度有所起伏,如图8所示。图9为地杂波的多普勒频谱,仅存在微小的多普勒频移,是地面植被摇曳、风速等造成的,这一特点很好地拟合了实际情况中的地杂波。

图6 双基地MIMO雷达地杂波谱

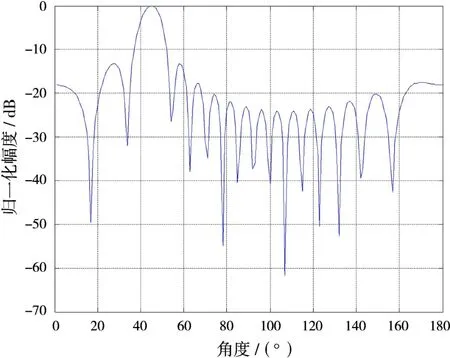
图7 阵列天线方向图

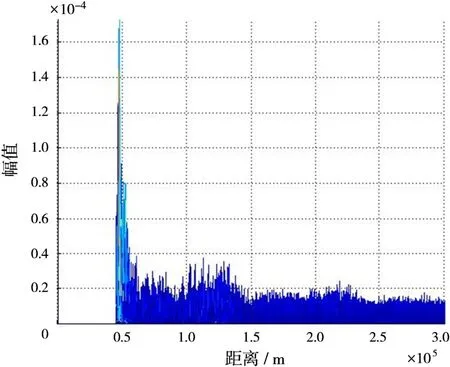
图8 距离维MTD结果

图9 双基地MIMO雷达地杂波多普勒频谱

5 结束语

本文提出了一种在发射角和接收角分辨率范围内,通过满足距离分辨率的等距离环将地面划分为雷达不可分辨的杂波单元的方法以及杂波划分预存储的技术,极大地减少了杂波仿真运算量。通过仿真分析证明了该方法的有效性,最后分析了双基地MIMO雷达杂波特性,有助于对双基地MIMO雷达杂波抑制和杂波背景下目标检测的研究。

[1]李均阁.雷达技术发展综述及多功能相控阵雷达未来趋势[J].甘肃科技,2012,28(18):19-22.

[2]何子述,韩春林,刘波.MIMO雷达概念及其技术特点分析[J].电子学报,2005,33(Z1):2441-2445.

[3]刘红明,何子述,王荣海.一种基于MIMO技术的多基地防空雷达系统[C]∥信息产业部雷达网第十七届年会,南京:南京电子技术研究所,2007.

[4]蔡茂鑫,舒其建,李勇华,等.MIMO雷达射频隐身性能的评估[J].雷达科学与技术,2013,11(3):267-270.

[5]NICHOLA J W.双基地雷达[M].张祖稷,吴曼青,等译.合肥:机电部38所,1992:81-82.

[6]王占广,刘红明,李军,等.双基地MIMO雷达杂波建模与分析[J].现代雷达,2012,34(5):31-34.