雷达组网协同探测范围研究∗

(中国电子科技集团公司第二十研究所,陕西西安710068)

0 引言

现代战争的范围已经从陆、海、空、天扩展到信息空间,谁取得了制信息权,谁就将取得战争的胜利。战场信息来自于不同平台上的各种传感器,因此,如何利用传感器进行协同探测,快速、有效地获得目标信息是当前一项重要的研究课题[1]。

多部雷达波束指向同一区域同时探测同一目标是一种有效的协同探测方式,可以增加对目标的稳定跟踪距离,提早建立目标航迹,扩大武器的有效使用范围,提高雷达传感器抗干扰能力和航迹连续性。

目标的雷达横截面积(Radar Cross Section,RCS)随视角变化而起伏[2]。起伏的RCS导致雷达作用距离和检测概率发生改变。文献[3]推导了一种高精度的雷达检测概率计算模型,并对雷达网综合检测性能进行了评估;文献[4]给出了分布式检测体制的雷达网性能计算方法。但是这些模型和方法均是针对非起伏目标提出,并没有涉及实际中更为常见的起伏目标的情况。

针对雷达组网对起伏目标协同探测范围计算问题,提出了一种极值假设估计法。在对目标起伏特性进行分析时,发现不同雷达在同一时刻观测到起伏目标的RCS的相关性未知,不满足传统的“或”准则检测融合使用条件。为此,首先推导了当相关系数ρ=0(完全不相关)和ρ=1(完全相关)的两种极限情况下雷达组网检测概率;然后对“或”准则进行修改,计算获得了雷达组网对起伏目标的协同探测范围及最佳雷达布站方案;最后通过仿真实验验证了算法的有效性。

1 目标起伏特性

Swerling模型是关于RCS起伏的统计和相关特性的5种标准统计假设,即Swerling 0、Ⅰ、Ⅱ、Ⅲ和Ⅳ型,它们已经被证明适用于多种雷达目标幅度的变化。Swerling 0假设目标RCS没有起伏。SwerlingⅠ假设接收到的目标回波振幅在任意一次扫描间都是恒定的(完全相关),但是从一次扫描到下一次扫描之间是独立的(不相关)、服从瑞利分布的随机变量。横截面积的概率密度函数为

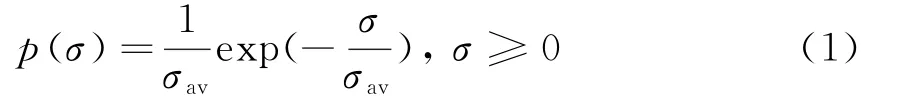
式中,σav为所有横截面积的平均值。SwerlingⅢ假设在一次扫描内RCS为常数,并且与从扫描到扫描是无关的,但概率密度函数为

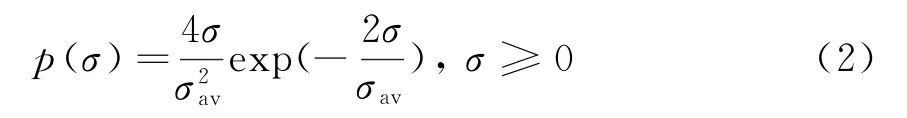
SwerlingⅠ、SwerlingⅢ要比其他情况更多地用于描述起伏目标的RCS统计[2]。因此,接下来将重点对这两种情况及非起伏情况进行研究。

2 协同探测范围计算

2.1 非起伏目标

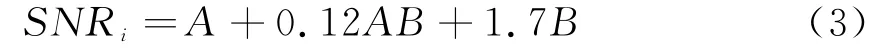
式中,SNRi为信噪比,A、B分别为虚警概率和检测概率的函数,,B=。

图1是按照式(3)画出的检测概率、虚警概率与信噪比之间的关系。从图中可以看出,当虚警概率不变时,信噪比越大,则检测概率越高;如果信噪比不变,虚警概率越小,则检测概率越低。图2是雷达手册中非起伏目标下,所需信噪比与检测概率、虚警概率的关系。由图1与雷达手册中的标准曲线对比可知,图1与非起伏目标的检测概率曲线吻合。

图1 检测概率、虚警概率与信噪比的关系

图2 在单脉冲、线性检波和非起伏目标情况下,所需信噪比(可见度系数)与检测概率、虚警概率的关系

将式(3)整理可得

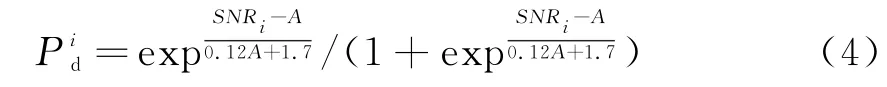
式中,A同式(3)。

N部相同雷达采用“或”准则[6]对目标的总检测概率为

总虚警概率为

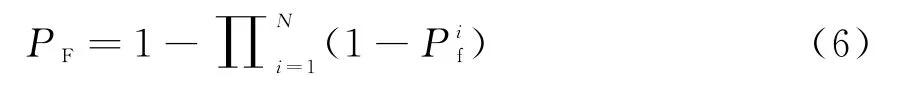
将式(5)、(6)结果代入式(3),获得N部相同雷达的总信噪比SNR。

根据雷达公式可以得出,当N部相同雷达对目标进行探测的信噪比为SNR时,其距目标距离为

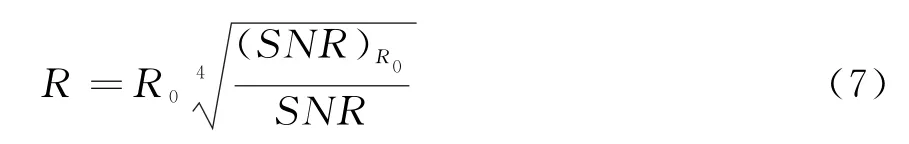
式中,(SNR)R0为对应于目标在R0处的信噪比。

2.2 起伏目标

2.2.1 检测概率、虚警概率与信噪比的关系

(1)SwerlingⅠ型目标

式中,SNRi为信噪比,Pif为虚警概率,Pid为检测概率。

图3是按照式(8)画出的Swerling I型起伏目标的检测概率、虚警概率与信噪比之间的关系。图4是雷达手册中,起伏目标情况下,所需信噪比与检测概率、虚警概率的关系。图3中Pd=0.9所需信噪比与图4中脉冲数为1所需信噪比相同。

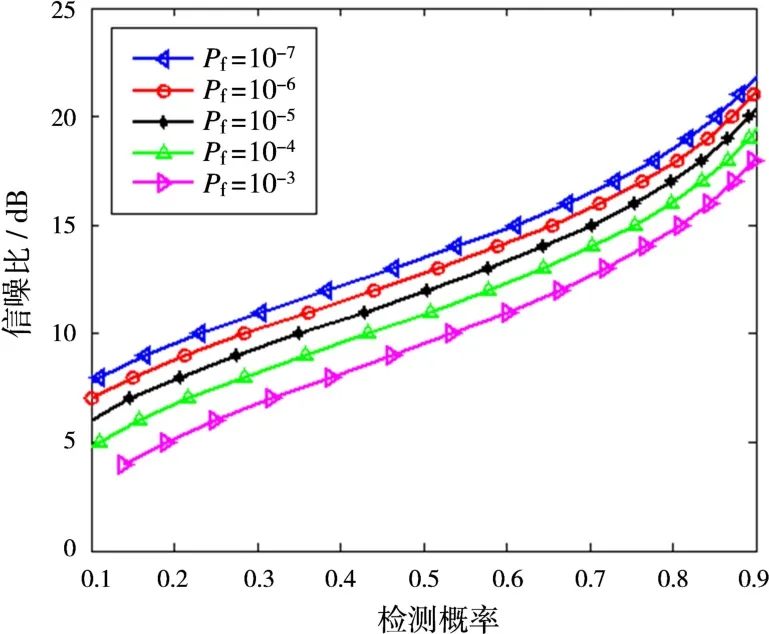
图3 检测概率、虚警概率与信噪比的关系(Swerling I型起伏目标)

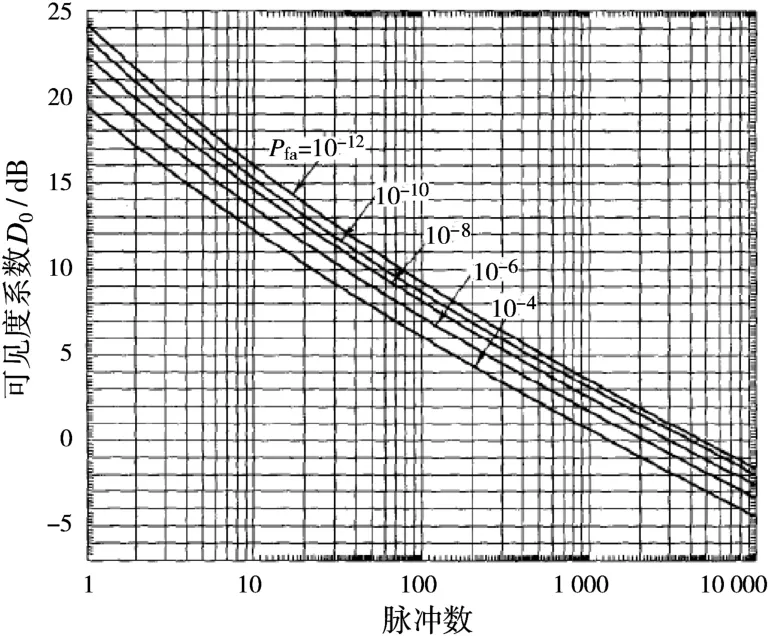
图4 在平方律检波、Swerling I型起伏目标和P d=0.9情况下,所需信噪比(可见度系数)与非相参积累脉冲数的关系

将式(8)整理可得

(2)SwerlingⅢ型目标

对于SwerlingⅢ型起伏目标而言,当积累脉冲数np=1,2时,第i部雷达Pid、Pif和SNRi三者之间的关系满足

图5是按照式(10)画出的SwerlingⅢ型起伏目标的检测概率、虚警概率与信噪比之间的关系。

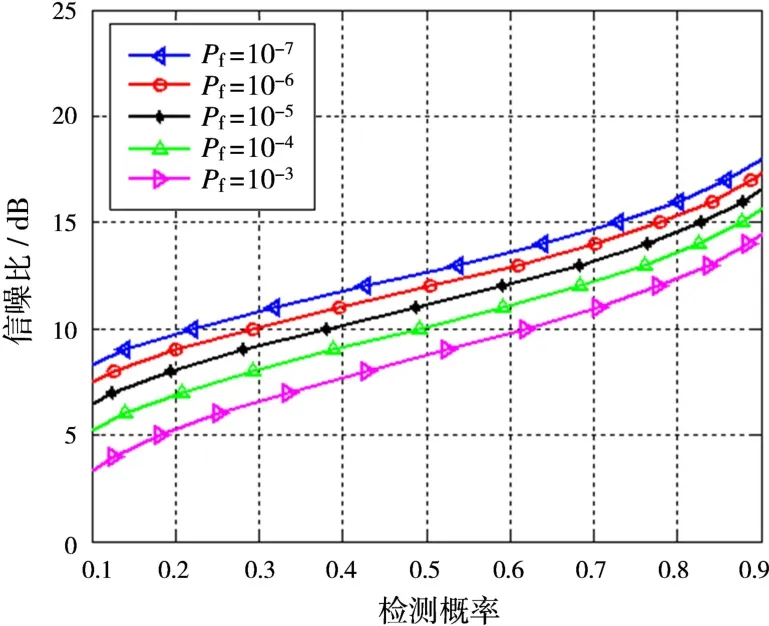
图5 检测概率、虚警概率与信噪比的关系(SwerlingⅢ型起伏目标)

2.2.2 雷达组网联合检测概率

N部相同雷达采用“或”准则对目标的总检测概率为

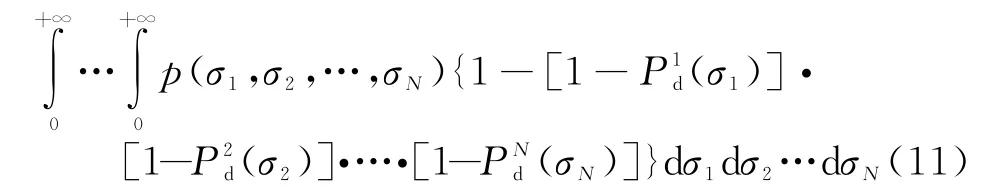
当目标起伏时,由于不同雷达对起伏目标观测值的相关性未知,需要考虑完全相关与完全不相关(独立)的两种极限假设情况(实际情况中,目标截面积起伏相关性介于二者之间),对雷达稳定跟踪距离的改善程度分别进行讨论。

(1)假设不同雷达间目标截面积起伏完全相关

当N部相同雷达同时探测目标,假设目标对于不同雷达呈现出完全相关的起伏特性(如图6(a)所示),有,则式(11)可以简化为

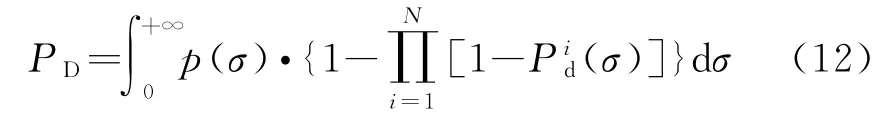
(2)假设不同雷达间目标截面积起伏完全不相关

当N部相同雷达同时探测目标,假设目标对于不同雷达呈现出完全不相关(独立)的起伏特性(如图6(b)所示,图中箭头所示为某一时刻,某部雷达探测到目标截面积大,而另一部雷达可能探测到目标截面积小),式(11)可以化简为

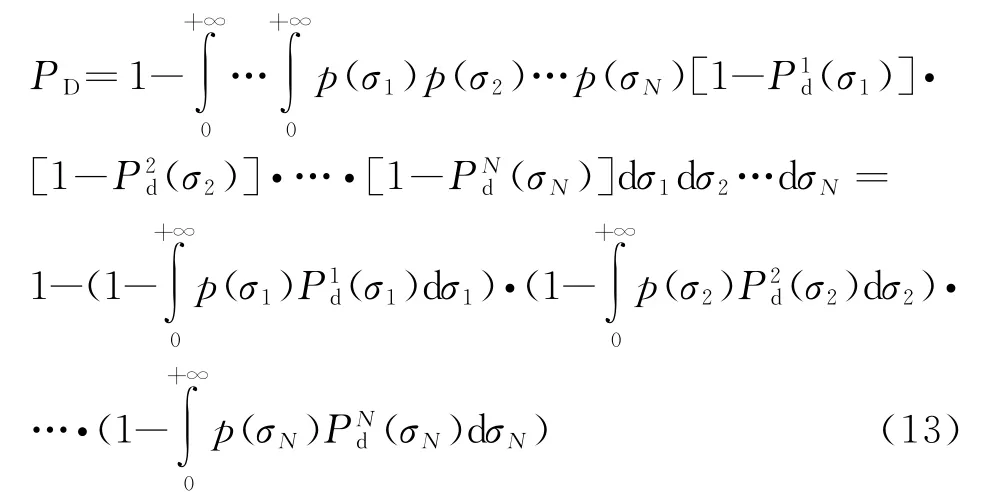
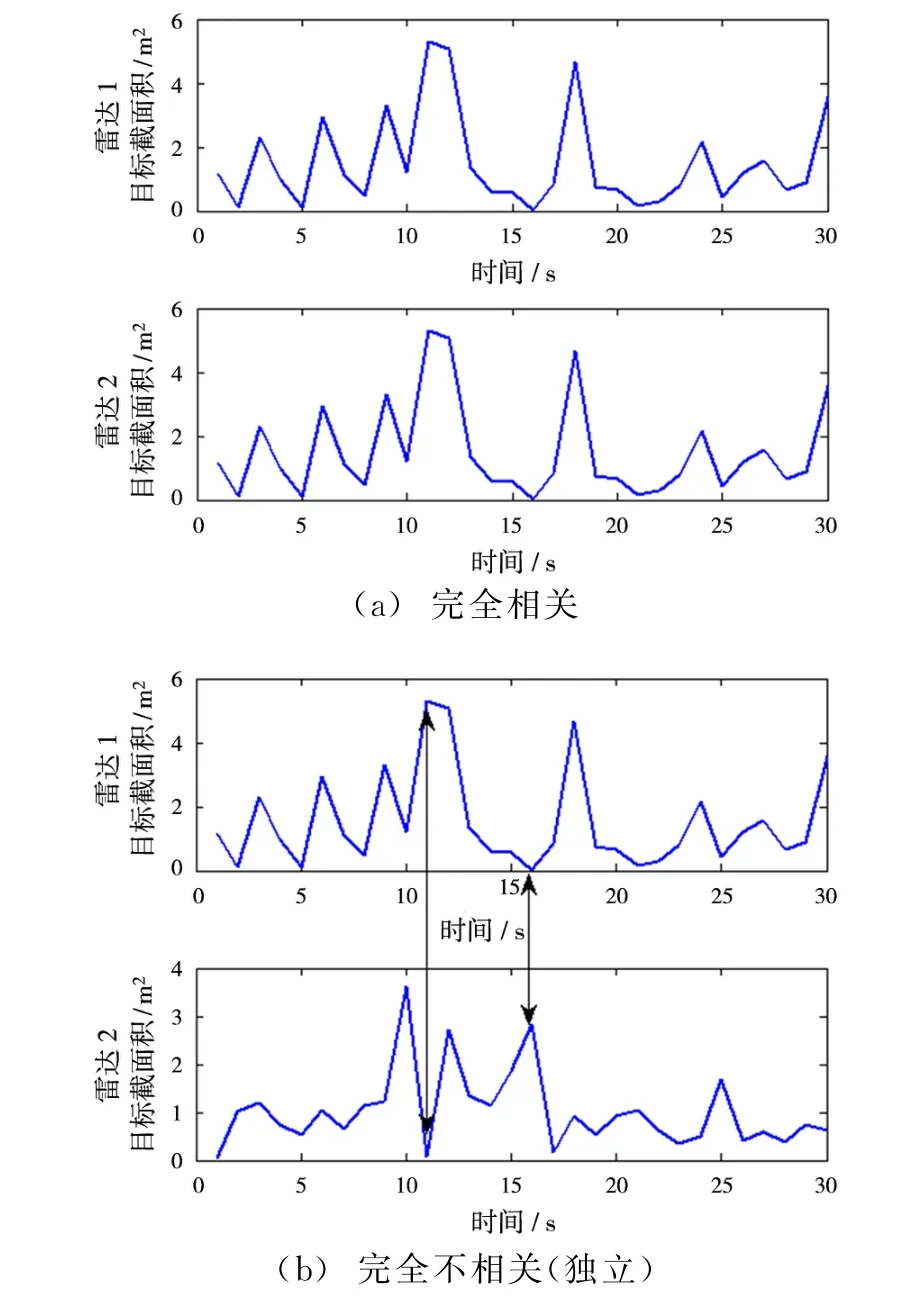
图6 假设目标对于两部雷达呈现出不同的起伏特性

2.2.3 雷达组网协同探测范围

将式(12)、(13)分别代入式(8)、(10),获得N部相同雷达的总信噪比SNR。再根据式(7),即可获得当目标对不同雷达呈现出完全相关、完全不相关起伏特性时的稳定跟踪距离。

3 仿真实验

本小节旨在通过仿真手段具体分析雷达网对起伏目标协同探测范围的改善情况。仿真中假设对于σav=2 m2,R=160 km的目标,当Pf=10-6时,Pd=0.9;目标起伏分别服从Swerling I型、SwerlingⅢ型统计模型。

图7是协同探测对雷达稳定跟踪距离的改善程度。从图中可以看出,协同探测对非起伏目标的稳定跟踪距离有一定改善,对于起伏目标稳定跟踪距离改善明显,并与目标的起伏特性相关,Swerling I型目标的改善程度处于带圈虚线与带星号虚线之间,SwerlingⅢ目标的改善程度处于带圈实线与带星号实线之间。

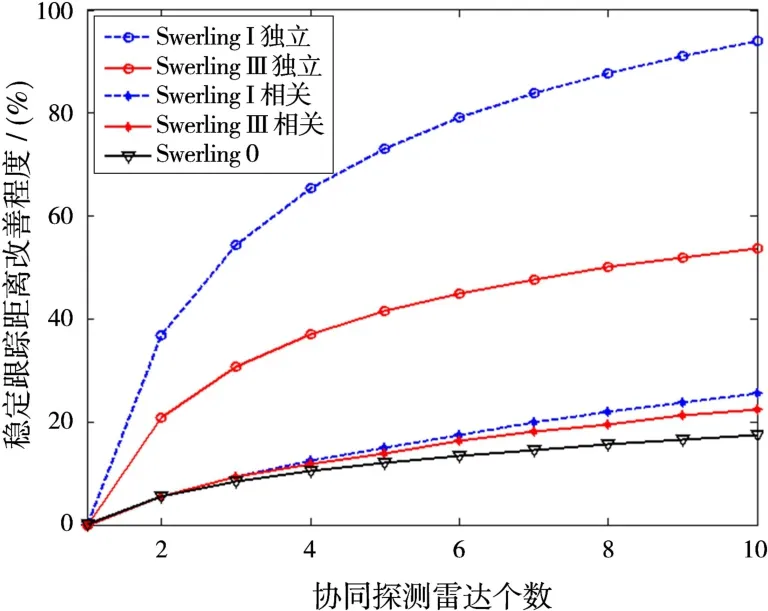
图7 协同探测对雷达稳定跟踪距离的改善程度

从图8和表1可以看出,在目标截面积起伏完全相关情况下,两部雷达融合后的检测概率高于单部雷达,Pd协同=0.9时距目标距离相比于单雷达增加了5.62%;在目标截面积起伏完全不相关情况下,两部雷达融合后的检测概率远高于单部雷达,对于Swerling I型目标,Pd协同=0.9时距目标距离相比于单雷达增加了36.7%;对于SwerlingⅢ型目标,Pd协同=0.9时距目标距离相比于单雷达增加了20.83%。在实际情况中,目标截面积起伏相关性介于上述二者之间,所以,对于Swerling I型目标稳定跟踪距离的改善程度为5.62%～36.7%;对于SwerlingⅢ型目标稳定跟踪距离的改善程度为5.62%～20.83%,而对非起伏目标的稳定跟踪距离改善程度为5.46%。

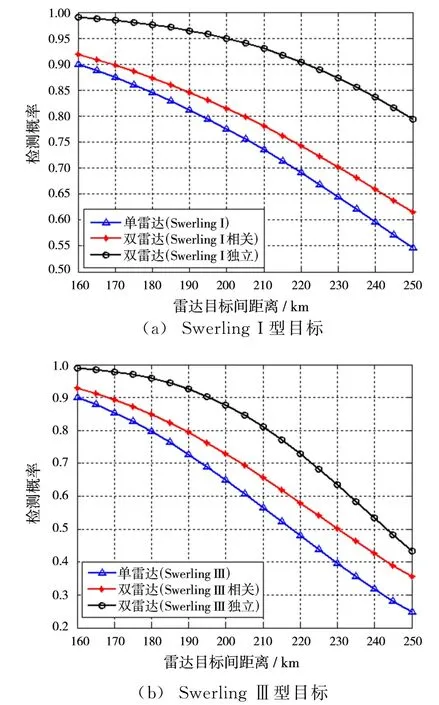
图8 起伏目标的检测概率

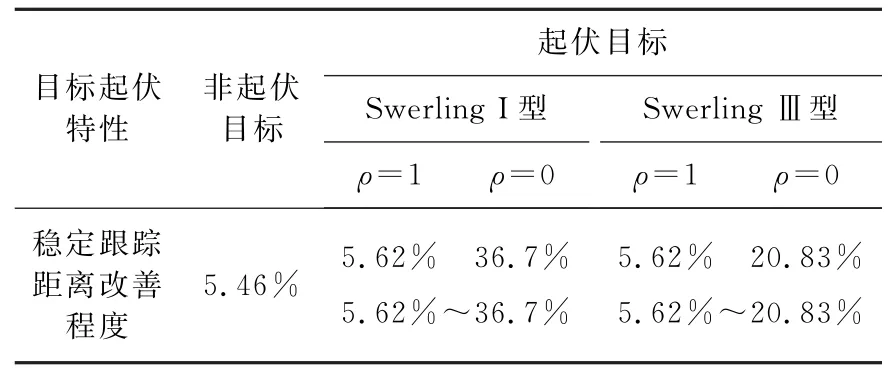
表1 两部相同雷达协同探测对稳定跟踪距离的改善程度

图9是三角形布站,Pd=0.9,Pf=10-6,3部相同雷达协同探测的威力范围。图中,实线圈由外至内依次为不同雷达间目标截面积起伏完全不相关、完全相关、非起伏时协同探测威力范围增加区域,后两者由于范围接近,在图中曲线重合。3个虚线圈内区域表示3部雷达未协同的威力范围。从图中可以看出,在任意两雷达连线垂直方向稳定跟踪距离改善较为明显。

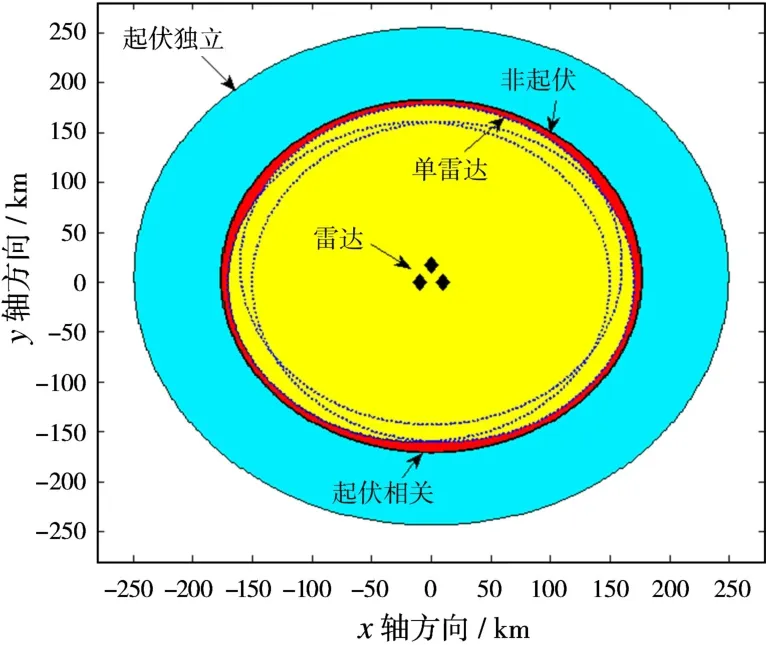
图9 三角形布站(Swerling I型目标)

4 结束语

在对起伏目标进行协同探测时,同一时刻不同雷达所观测到目标的RCS是不一致的,并且存在一定的相关性。因此雷达组网对目标稳定跟踪距离不是一个固定的值,而是与目标环境相关的距离范围。本文从目标起伏特性出发,改进了检测融合算法,推导了多雷达组网联合检测概率计算模型,获得了其协同探测范围。通过仿真实验验证了算法的有效性,仿真结果可为雷达网布阵提供参考。

[1]张远,方青,曲成华.基于遗传算法的组网雷达优化部署[J].雷达科学与技术,2014,12(1):76-80.ZHANG Yuan,FANG Qing,QU Cheng-hua.Optimal Deployment of Netting Radars Based on Genetic Algorithms[J].Radar Science and Technology,2014,12(1):76-80.(in Chinese)

[2]SKOLNIK M I.雷达系统导论[M].3版.左群声,许国良,马林,等译.北京:电子工业出版社,2006.

[3]赵志超,饶彬,王涛,等.雷达网检测概率计算及性能评估[J].现代雷达,2010,32(7):7-10.

[4]熊年生.基于分布式检测的雷达组网探测技术研究[J].雷达科学与技术,2012,10(4):363-366.XIONG Nian-sheng.Research on Radar Coordinated Detection Scheme Based on Distributed Detection Technique[J].Radar Science and Technology,2012,10(4):363-366.(in Chinese)

[5]DONALD W T,ALFRED J C.On Albersheim’s Detection Equation[J].IEEE Trans on Aerospace and Electronic Systems,1983,19(4):643-646.

[6]何友,王国宏,陆大纟金,等.多传感器信息融合及应用[M].2版.北京:电子工业出版社,2007.

[7]何友,关键,孟祥伟,等.雷达目标检测与恒虚警处理[M].2版.北京:清华大学出版社,2011.