导电聚合物驱动器的自适应滑模控制研究*

许 洋，王湘江，刘怀民

(南华大学机械工程学院，湖南衡阳421001)

0 引言

在过去十年里，基于吡咯、噻吩、苯胺等导电聚合物驱行器由于其功耗低、重量轻、结构简单、操作简便、无需高电压驱动，对磁场不敏感和工作无噪音等优点，已被作为高性能智能驱动器进行了广泛研究。这些驱动器也被称为人造肌肉，其工作原理基于离子在导电聚合物层的迁移［1-6］。大量的研究一直致力于构建其电化学机械行为模型，通过控制其弯曲变形以增强驱动器的定位能力。各国学者已经建立一些有效的数学模型［7-12］，但这些模型的精度和适应性需要进一步的研究。基于逆模前馈控制是一种开环控制方法［13］，这种方法无需要反馈的数据就能控制其弯曲位移［14］，但其不具有鲁棒性。

在已有研究的基础上，本研究首先采用递推最小二乘法，对所制作的能在空气介质中工作的多层弯曲型导电聚合物驱动器进行建模研究［15］。针对模型特性，提出了一种自适应滑模控制律来控制驱动器的弯曲位移。理论上证明了自适应滑模控制方法的稳定性。最后，通过实验证明控制该方法有较好的信号跟随能力。本研究中所使用的驱动器是一个多层(三层)的聚吡咯电活性聚合物驱动器，该驱动器可在空气和液体介质下工作。

1 数学模型的建立

多层驱动器的结构如图1所示。笔者所研究的导电聚合物驱动器最外层为活性聚吡咯层，中间层是能容纳液体电解质的多孔隔板(偏二氟乙烯PVDF)，PVDF 两侧是很薄的镀金层。该多层结构能够产生类似于双层悬臂结构的简单弯曲运动。当电势差或电流通过聚合物(聚吡咯)的电极时，驱动器由于电化学反应作用其尖端发生弯曲产生机械运动。

图1 多层驱动器的结构

为实现驱动器的精确运动，测控系统的实验装置如图2所示。

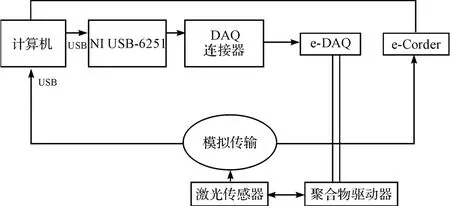
图2 实验装置示意图

驱动器的输入电压信号先由计算机输出，该系统包含了NI USB-6251，DAQ 及电子数据采集接口。电压信号被发送到驱动器的两电极。驱动器的尖端的位移由非接触式激光位移传感器(NCDT-1700-10)测量。

驱动器工作包含了电、化学和机械过程。由理论分析可得驱动器的传递函数为［16］:

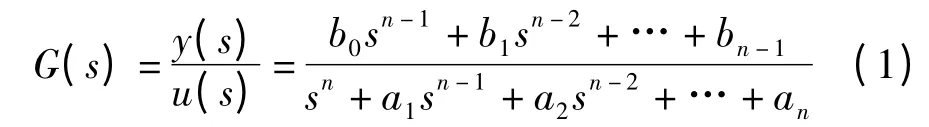
式中:u(s)—输入电压信号，y(s)—输出位移信号。

最小二乘递归识别方法可以用来在线识别驱动器的参数。该数学模型(1)可以表述为:

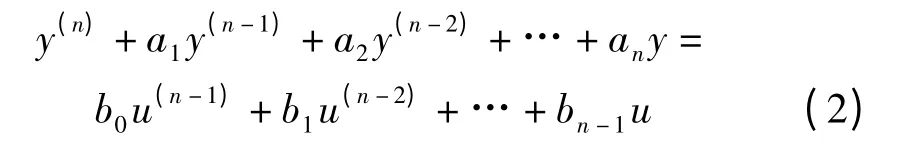
参数θ 定义为:

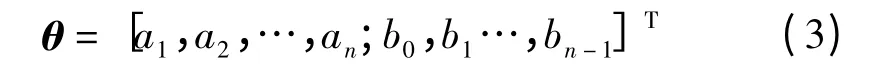
变形参数φ(t)由下式给出:

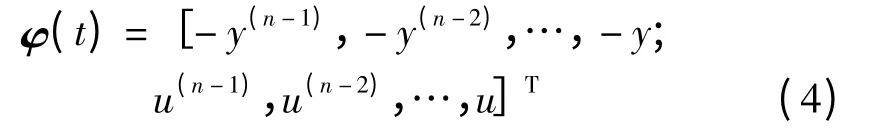
公式(2)可表述成:

递推最小二乘算法为:

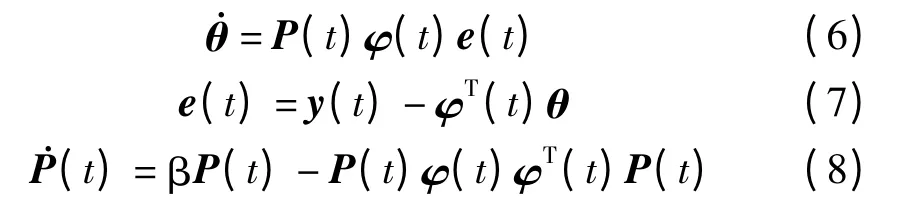
式中:β—一个正常数;P(t)—一个对称的正定矩阵。

当n=2，式(1)可以简化为一个二阶系统，参数向量θ 可以写成:

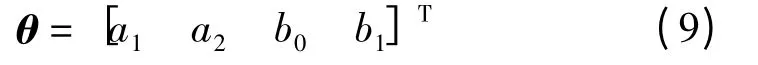
变形向量可写成:

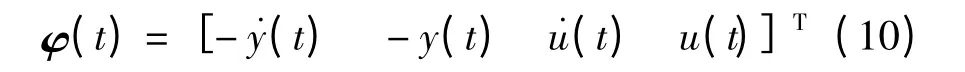
为了消除高频干扰，向量φ(t)通过一个低通滤波器H(S)进行滤波:

式中:α1，α2—正常数。

实验用驱动器的尺寸为15 mm ×4 mm ×0.17 mm。二阶系统的参数的变化如图3所示。

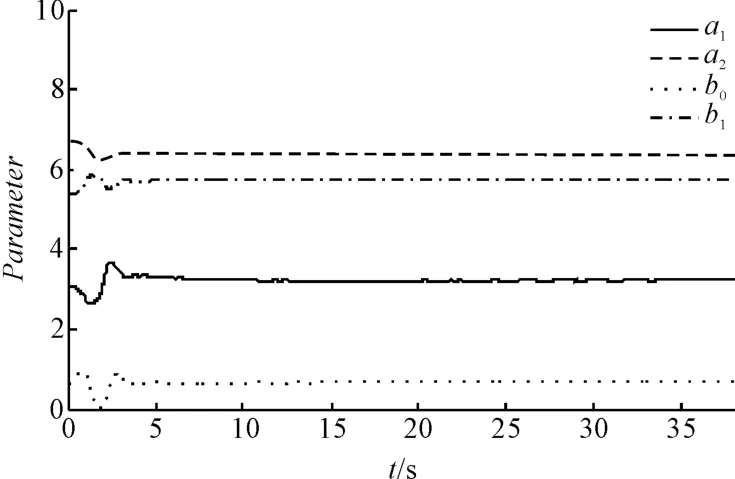
图3 模型参数的收敛性

在线识别模型输出和驱动器的实验输出对比如图4所示。可以看出将系统看成二阶系统其误差非常小。精确的驱动器模型可由下式给出:

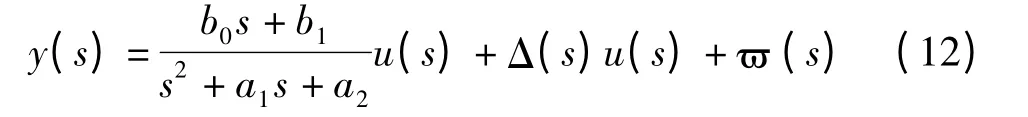
式中:Δ(s)—未建模的动态参数，ϖ(s)—测量噪声。参照图5，可知Δ(s)很小且有界，ϖ(s)有界的。

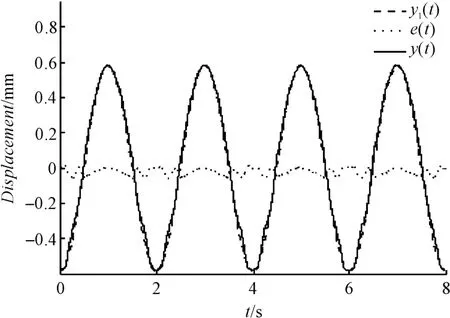
图4 在线识别系统的实验结果

驱动器模型可简化为二阶线性系统进行分析，具有如下结构:

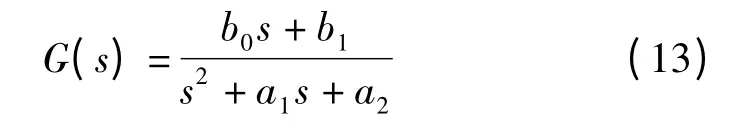
由式(13)可得:

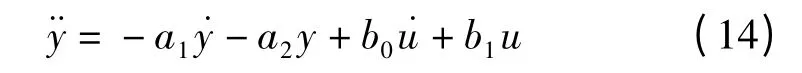
2 自适应滑模控制器

滑模控制律的切换函数定义为:

式中:yd—期望轨迹;λ—一个正常数。

由式(14，15)可得:

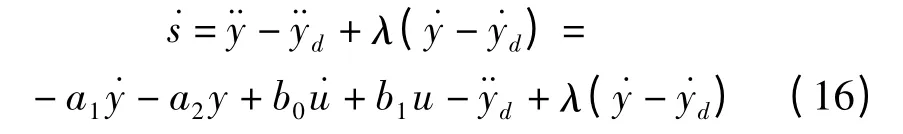
为了保证正常运动段的品质，可采用如下趋近律:

其中:Kd＞0。

由公式(16，17)可得:

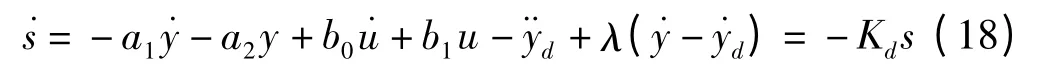
因此:

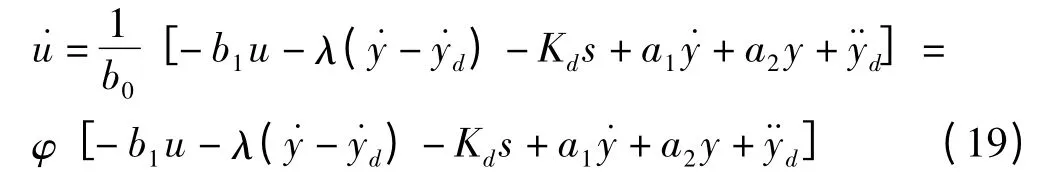
式中:φ =1/b0，使用以下定义来证明所提出的控制方法的稳定性:

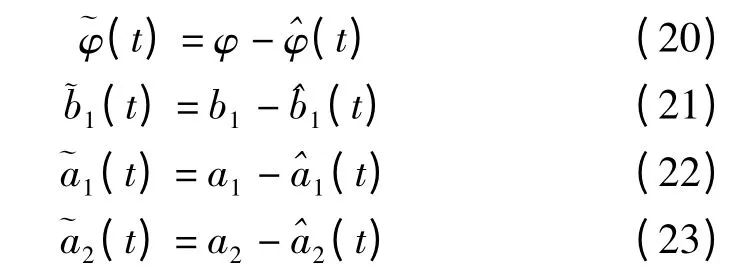
式(19)可写为:

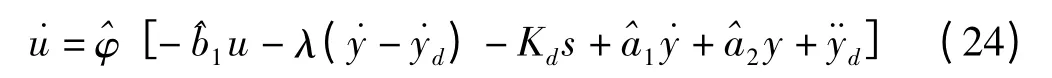
如果:

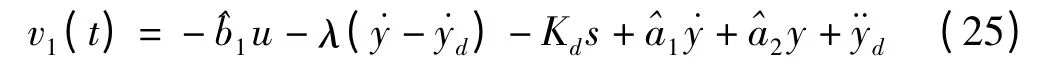
驱动器的滑模控制律可写为:

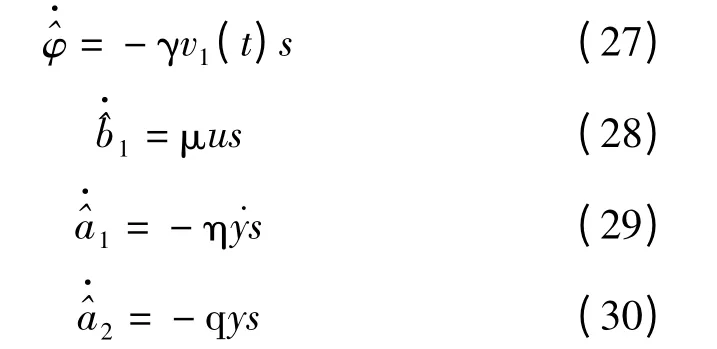
式中:γ，μ，η，q—正常数。

定理:对于由公式(12)给出的系统，基于公式(27 ～30)给出的滑模控制器的自适应律，对于所有有界信号都存在，当t→∞时y(t)→yd(t)。

证明:使用式(16，20 ～23，26)和式中s 的定义，并注意到:

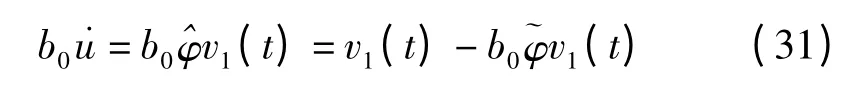
有:

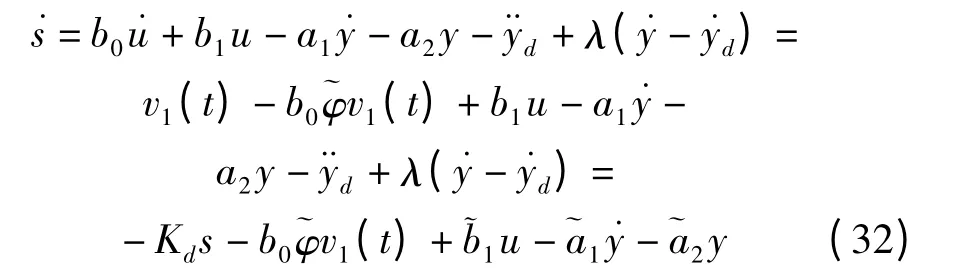
定义如下的Lyapunov 函数:

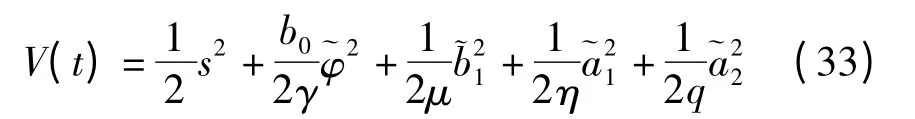
其导函数:

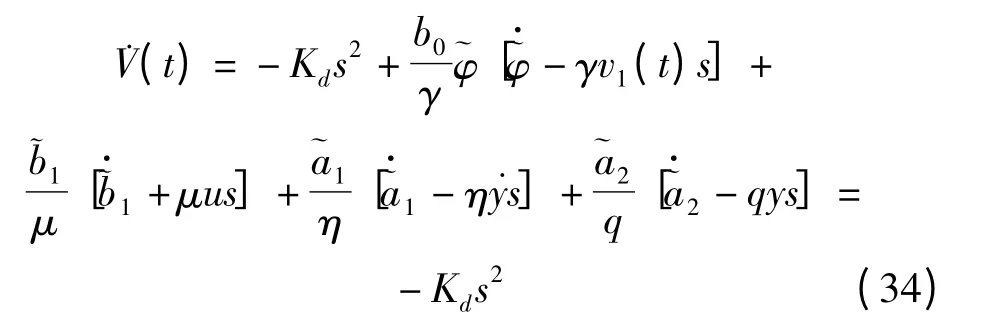
式(33，34)表明:V(t)为非递增函数，由Lyapunov稳定性理论可知系统稳定。

3 实验结果与讨论

由于式(25 ～30)中的参数Kd，λ，γ，μ，η 和q 可进行仿真得到参数初值。函数s 当ε=0.001 25 时，由s－εsat(s/ε)替换，以减轻系统输出的抖振现象。sat(·)是饱和函数。

为验证控制率的实际效果，输入期望的轨迹yd=1.5sin(ωt)，选择不同频率范围;ω = 0.25 rad/s，0.5 rad/s，1.0 rad/s，2.0 rad/s。实验结果如图(5 ～9)所示(其中:e(t)—驱动器的输出位移y(t)与期望输入yd(t)之间的跟踪误差)。

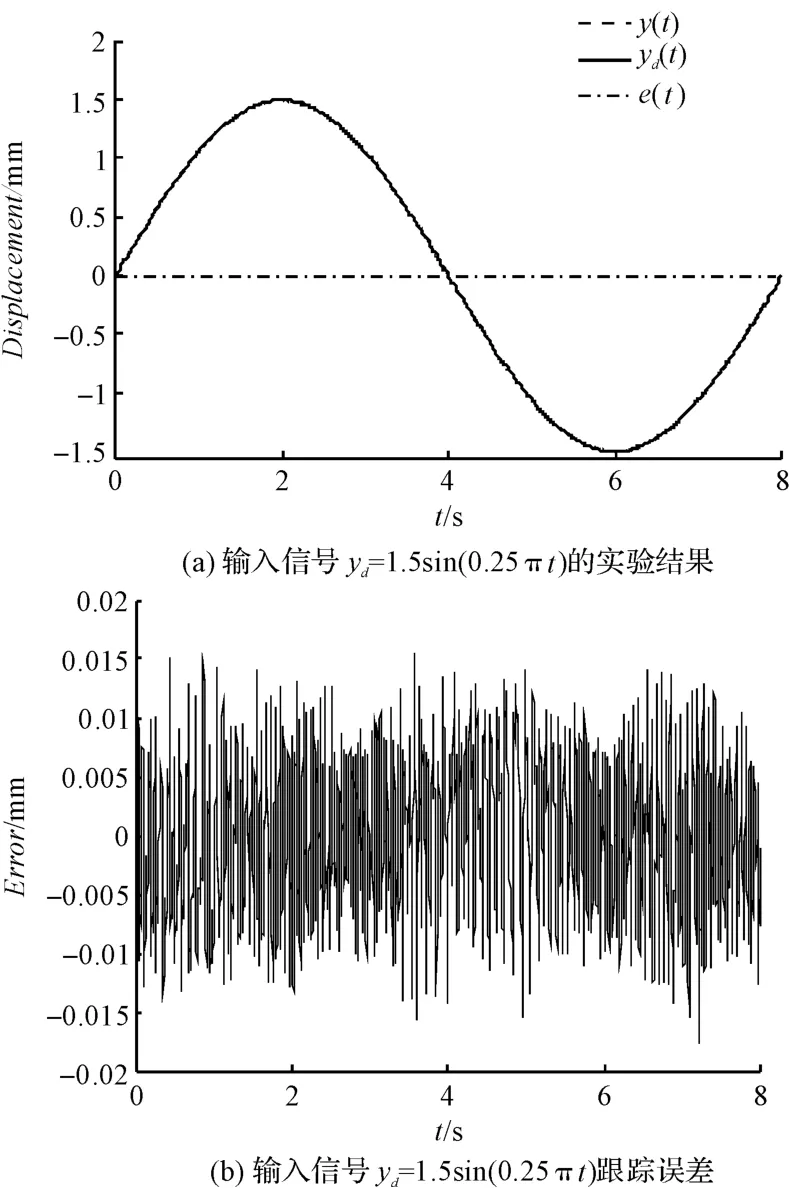
图5 输入信号yd =1.5sin(0.25πt)的控制效果

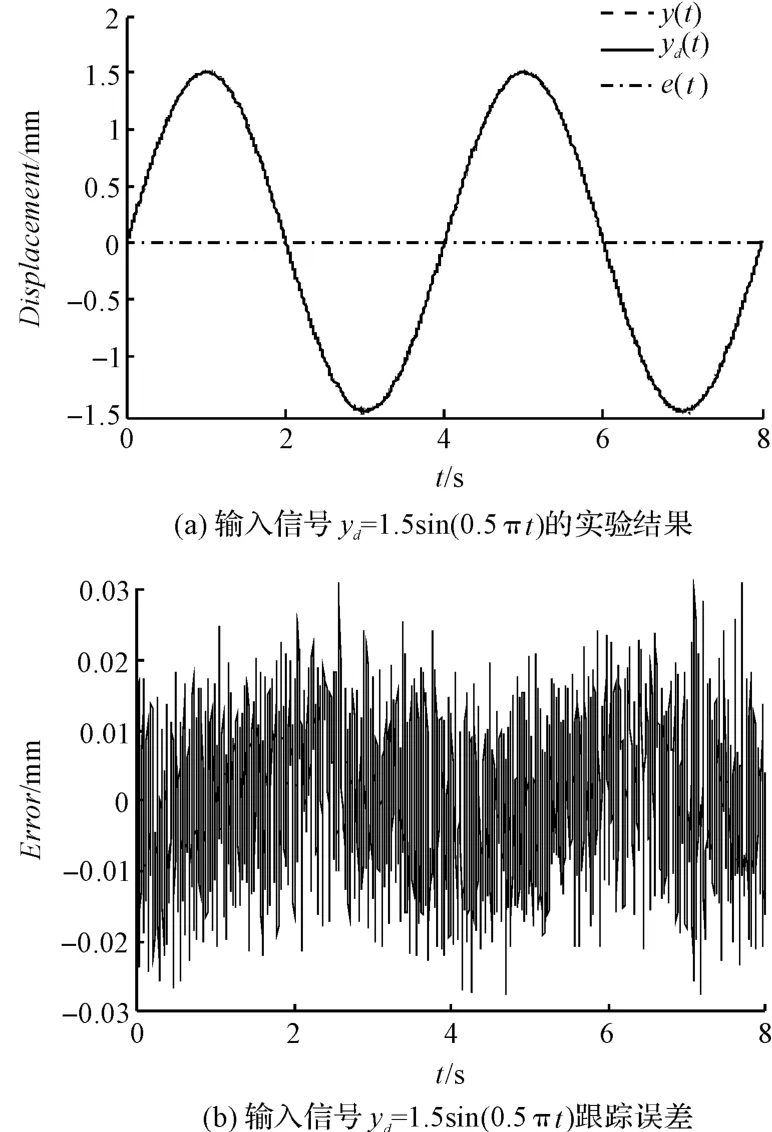
图6 输入信号yd =1.5sin(0.5πt)的控制效果

此外，自适应滑模控制器的动态位移响应由两个混合正弦轨迹进行验证;轨迹A(yd=1.2sin(0.25πt)+0.3sin(πt))如图9所示，轨迹B(yd=1.2sin(πt)+0.3sin(4πt))如图10所示。跟踪误差的均方根平方(RMS)如表1、表2所示。RMS 由下式给出:

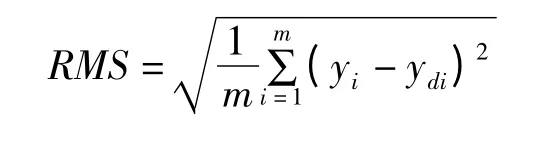
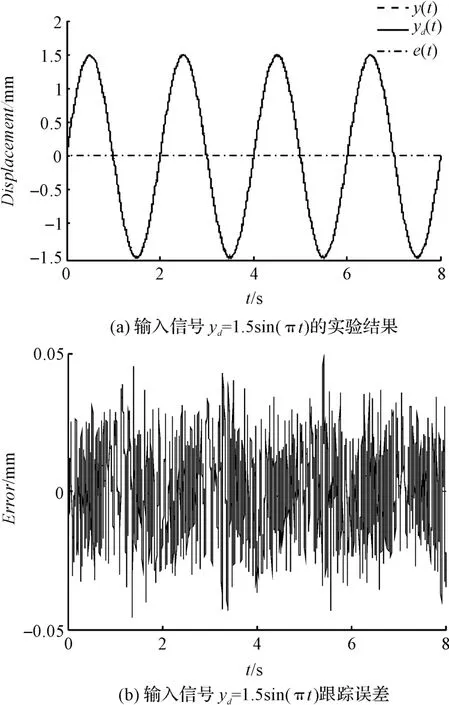
图7 输入信号yd =1.5sin(πt)的控制效果

图8 输入信号yd =1.5sin(2πt)的控制效果

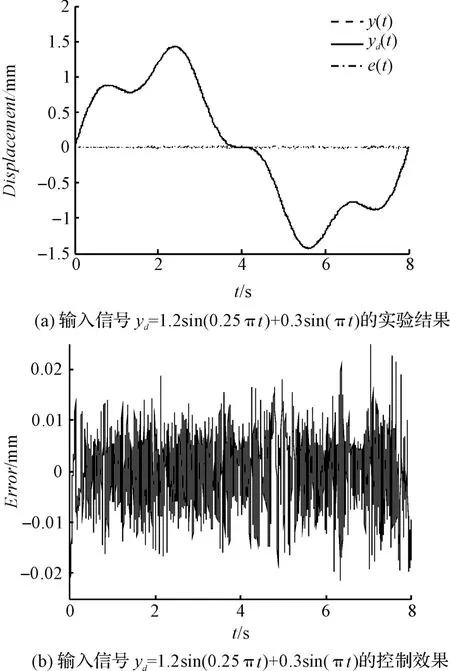
图9 输入信号yd =1.2sin(0.25πt)+0.3sin(πt)的控制效果

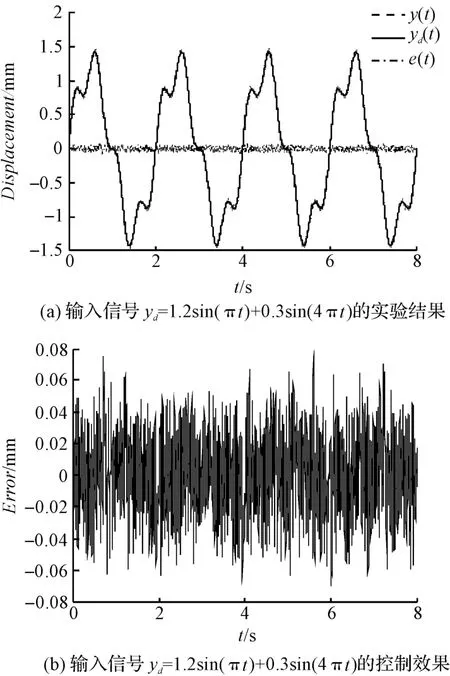
图10 输入信号yd =1.2sin(πt)+0.3sin(4πt)的控制效果

表1 yd =1.5sin(ωt)的均方根误差

表2 混合正弦轨迹的均方根误差

位移输出和信号跟踪误差如图5 ～10所示。输出位移y(t)与期望输入yd(t)如图5(a)～10(a)所示，从图上看输出位移y(t)与期望输入yd(t)几乎重合。这说明，自适应滑模控制方法表现出优异的跟踪特性。控制输入和位置跟踪误差如图5(b)～10(b)所示。由位置跟踪误差表明:控制方法很好的补偿了简化模型的不确定性和未建模动态，位置跟踪误差的均方根在0.032 mm 内，且状态稳定，说明所提出的自适应滑模控制方法是有效的。同时，如图(5 ～10)、表(1 ～2)所示，频率越高，RMS 也越大。

实验结果说明，自适应滑模控制方法是稳定的，且能很好地跟随期望的轨迹。需要注意的是，自适应滑模控制方案跟踪误差没有完全消除，原因主要是由于测量噪声造成的，且信号频率越高，噪声影响越大。

4 结束语

本研究提出一种自适应滑模控制方法来控制弯曲型导电聚合物驱行器的尖端位移输出。使用递归最小二乘法来在线识别驱动器的系统模型参数，由辨识结果可知，驱动器可简化为二阶系统，简化模型使控制系统的设计和实现变得更加容易。为使控制器具有适应性和鲁棒性，采用自适应滑模控制律来实现对驱动器的动态精确控制。此种控制律的实施是可行的，并且仅仅只需要知道一个简化的导电聚合物驱行器模型以及未建模动态和不确定性的边界。自适应滑动模式控制方法的稳定性已在理论上证明，实验也显示控制系统能有效地控制驱动器的弯曲位移。

［1］VIDAL F，PLESSE C，PALAPRAT G，et al.Conducting IPN actuators:From polymer chemistry to actuator with linear actuation［J］.Synthetic Metals，2006(156):1299-1304.

［2］ALICI G，DEVAUD V，RENAUD P，et al.Conducting polymer microactuators operating in air［J］.Journal of Micromechanics and Microengineering，2009，19(2):1-9.

［3］HAN Gao-yi，SHI Gao-quan.Conducting polymer electrochemical actuator made of high-strength three-layered composite films of polythiophene and polypyrrole［J］.Sensors and Actuators B，2004，99:525-531.

［4］GAIHRE B，ALICI G，SPINKS G M，et al.Synthesis and performance evaluation of thin film PPy-PVDF multilayer electroactive polymer actuators［J］.Sensors and Actuators A，2011，165(2):321-328.

［5］HAN Gao-yi，SHI Gao-quan.High-response tri-layer electrochemical actuators based on conducting polymer films［J］.Journal of Electroanalytical Chemistry，2004(569):169-174.

［6］FUCHIWAKI M，TANAKA K，KANETO K.Planate conducting polymer actuator based on polypyrrole and its application［J］.Sensors and Actuators A，2009(150):272-276.

［7］ALICI G，PUNNING A，SHEA H R.Enhancement of actuation ability of ionic-type conducting polymer actuators using metal ion implantation［J］.Sensors and Actuators B，2011，157(1):72-84.

［8］SHOA T，YOO D S，WALUS K，et al.A dynamic electromechanical model for electrochemically driven conducting polymer actuators［J］.IEEE/ASME Transactions on Mechatronics，2011(16):42-49.

［9］WANG X，SHAPIRO B，SMELA E.Development of a model for charge transport in conjugated polymers［J］.Journal of Physical Chemistry，2009(113):382-401.

［10］JOHN S W，ALICI G，COOK C D.Validation of a resonant frequency model for polypyrrole trilayer actuators［J］.IEEE/ASME Transactions on Mechatronics，2008(13):401-409.

［11］ALICI G.An effective modelling approach to estimate nonlinear bending behaviour of cantilever type conducting polymer actuators［J］.Sensors and Actuators B，2009(141):284-292.

［12］DU Ping，LIN Xi，ZHANG Xin.A multilayer bending model for conducting polymer actuators［J］.Sensors and Actuators A，2010(163):240-246.

［13］阳 丹，王湘江.迟滞非线性系统辨识与补偿控制研究［J］.机电工程，2014，31(1):57-61，85.

［14］JOHN S W，ALICI G，CHRISTOPHER D.Cook 2010 inversion-based feedforward control of polypyrrole trilayer bender actuators［J］.IEEE/ASME Transactions on Mechatronics，2010，15(1):149-156.

［15］杨 毅，王湘江，曾庆生.导电聚合物驱动器的系统辨识和运动控制［J］.中南大学学报:自然科学版，2014，45(4):1085-1090.

［16］NGUYEN C H，WALLACE G G，ALICI G.Modelling trilayer conjugated polymer actuators for their sensorless position control［J］.Sensors and Actuators A，2005，185(1):82-91.