开关磁阻电动机转矩特性的检测与建模研究*
宋小川,王家军
(杭州电子科技大学自动化学院,浙江杭州310018)
0 引言
开关磁阻电动机特殊的定、转子双凸极结构,以及多变量耦合且工作于磁饱和状态等特征,使得电磁转矩的解析计算十分困难[1]。如何在满足工程精度要求的前提下,以近似的方法获取开关磁阻电动机的转矩特性是开关磁阻电动机研究中的一项重要内容。通常开关磁阻电动机的电磁转矩可利用有限元分析法或基于磁链模型计算得到。有限元分析法先通过电动机的定、转子几何尺寸等相关物理参数计算出定、转子极附近的磁场分布,再进一步求解得到电磁转矩[2]。磁链模型计算法则依据开关磁阻电动机的基本能量转换规律,先将各角度上的磁链对电流积分得到磁共能,再将各电流对应的磁共能对角度微分得到电磁转矩[3]。
本研究首先分别采用基于暂态电流和稳态电流的实验方法,对一台4 相8/6 极开关磁阻电动机的转矩特性进行检测,并根据转矩的实测数据用曲线拟合的方法得到转矩关于相电流和转子位置角的解析函数T(θ,i)。最后,为了提高拟合精度,提出一种基于区间分段的拟合方法对转矩特性进行拟合,最终所得转矩模型具有较高的拟合精度。
1 转矩特性的测量实验
由于开关磁阻电动机的各相绕组完全相同且相互独立,只需对其中的任意一相进行测量[4]。转矩特性T(θ,i)是相电流i 和转子位置角θ 的二元函数,因此实验将先对每一个特定角度的转矩-电流特性T-i 进行测量,再得到全周期完整的转矩特性T(θ,i)。实验过程中转子将会被固定在某一特定位置,并向绕组供以直流脉冲电压。通过用数字示波器记录实验中的转矩和电流波形及其对应的数值T(t)和i(t),如此便可得到该位置的转矩-电流特性T-i。要得到整个周期的转矩特性T(θ,i),需要对各转子位置进行上述实验。
实验电路原理图及实验平台如图1所示。
绕组经过功率开关元件IGBT 连接电源[5]。为了避免交流电源的谐波和电路中的RLC 振荡所引起的误差,该实验采用一种精密可调直流稳压电源供电。续流二极管D 在IGBT 关断时为绕组提供释放能量的通道,其通断由信号发生器来控制[6]。
本研究的实验对象为一台四相8/6 极开关磁阻电动机,其厂家给出的基本参数如表1所示。在实验之前需要对绕组阻值进行测量[7]。
1.1 基于暂态电流法的转矩测量
为了测量特定位置的转矩-电流特性,实验需要使用分度卡盘固定电动机的转子位置,此外还需要使用转矩测量仪来测量具体转矩数值。转矩测量仪输出为高频数字信号,为了便于通过示波器观察,需要通过数模转换模块将频率信号转化为电压信号。本研究在一个绕组周期上从对齐位置到非对齐位置进行了30 组实验,其主要步骤如下:
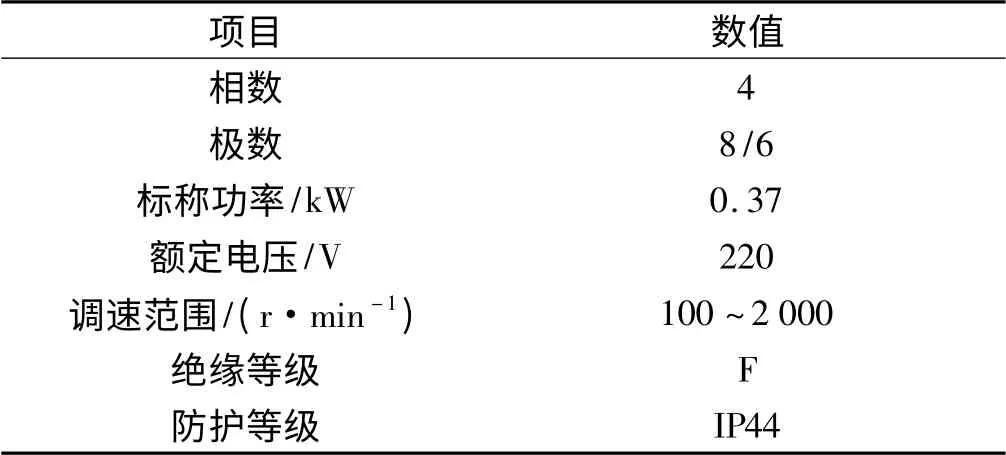
表1 被测样机基本参数
(1)用分度卡盘固定好转子位置,并用配置好的电源和触发信号去激励电路;
(2)用数字示波器观测并记录一个脉冲周期的电流-转矩波形及各采样点采样数据;
(3)解除分度卡盘的锁定,将转子往非对齐位置转动1°的机械角度,并重复(1)和(2)的操作;
当转子转动到非对齐位置时便完成了转矩特性的检测。部分位置的实验波形如图2所示。
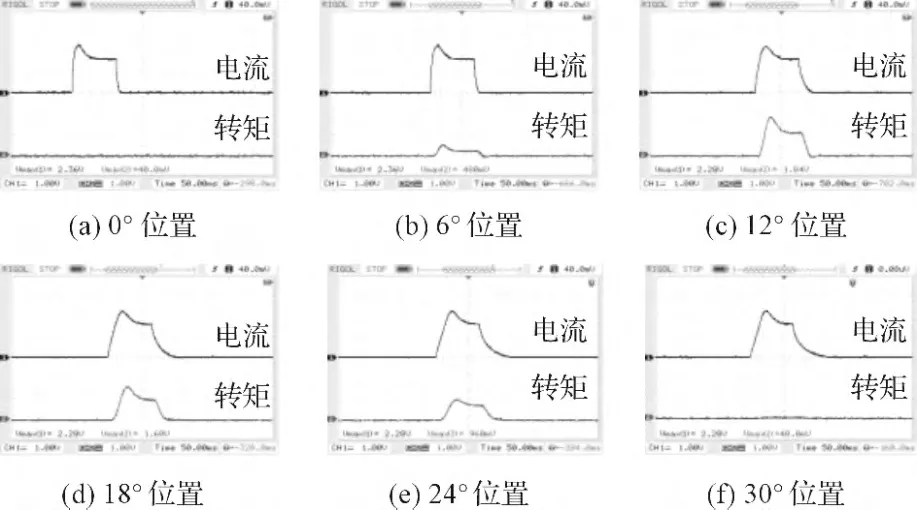
图2 不同位置的转矩-电流波形
通过实验波形可直观地体现各变量之间的变化趋势,但要建立精确的数学模型来找到各变量间的解析关系还需借助于具体的实验数据。示波器在记录实验波形的同时也采集了31 组对应电流和转矩的离散数据序列,为了获取各位置转矩与电流的对应关系,实验选取各位置上电流和转矩从零增长到最大值的单调区间内的采样值,其余的值舍弃。笔者根据实验数据用Matlab 在二维坐标中绘制出部分位置的转矩-电流波形,如图3所示。图中每一条曲线代表一个位置的电流-转矩特性。
本研究将各位置的电流-转矩特性所组成的转矩值矩阵转置,可得到不同电流值对应的位置-转矩特性如图4所示。
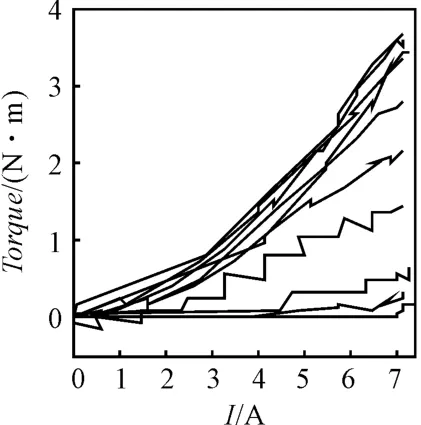
图3 不同位置的转矩-电流曲线
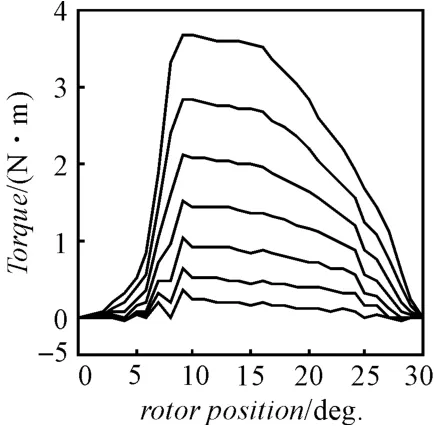
图4 不同电流的转矩-位置曲线
可见,随着电流的上升转矩值有明显波动,这是由于在暂态过程中示波器采样存在着电磁干扰,与此同时转子和转矩测量仪连接处的细微相对位移以及系统转动惯量和摩擦都会对转矩产生影响。该实验所采用的转矩测量仪是高精度仪器,这些机械干扰信号均会被转矩测量仪所捕获,因此实验结果的精确度并不理想。
1.2 基于稳态电流法的转矩测量
暂态电流法是一个动态采样过程,一方面电流和转矩采样序列中各采样点难以一一对应,另一方面在动态过程中采样电流和转矩总会有误差被示波器捕获。为了消除上述两种误差来源,本研究现采用基于稳态电流的方法进行转矩测量。稳态电流法将不对上升阶段的电流和转矩进行采样,而是等电流达到最大值并保持一定时间待其进入稳定状态后再分别对稳态电流和转矩进行采样,并分别取平均值。为了能够得到足够多的稳定状态下的数据采样点,需要将实验的采样周期和占空比增大,如此便可测得特定角度、特定电流所对应的转矩数值。实验方法在做出此改进之后,首先采样时间上的误差被消除,因为电流和转矩都已经处于稳定状态,它们的采样值在时间上总是对应的。其次对稳定阶段的值进行采样并取平均进行滤波也减小了实验误差对结果的影响。
采用稳态电流法所得前半周期部分位置部分电流对应的实验波形如图5所示。其中图5(a ~c)对应5°位置,图5(d ~f)对应15°位置,图5(g ~i)对应25°位置。
此时通过对称性可得后半周期的转矩特性,其对应的二维和三维曲线如图6所示。
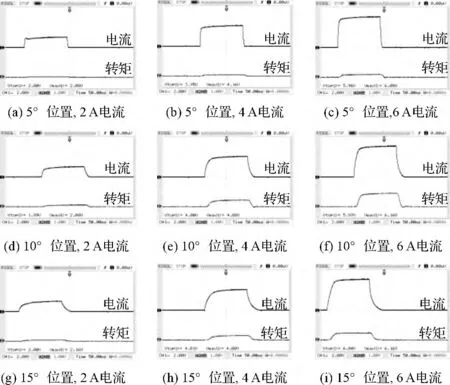
图5 各位置上不同电流对应的转矩波形
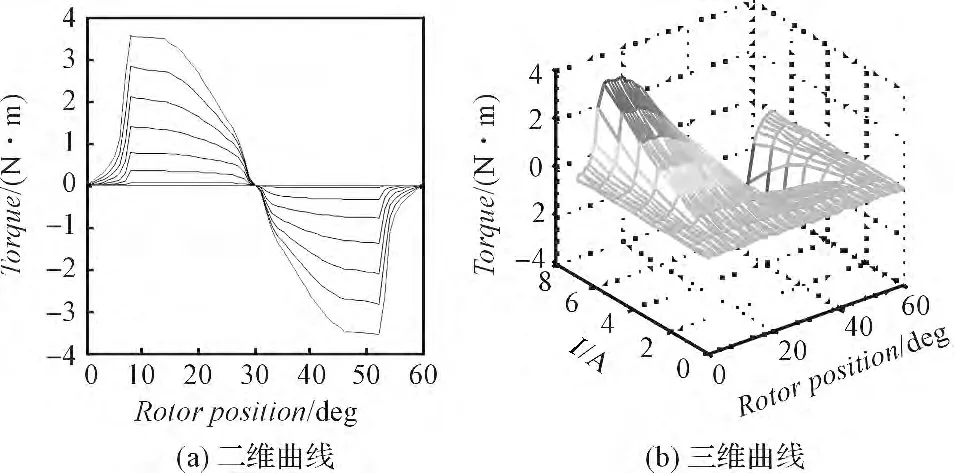
图6 实测转矩的2 维曲线和3 维曲线
图中所示曲线完全由实验结果直接描点绘图所制成,没有经过滤波或拟合的处理,从图中可以看出由原始数据所绘图形已经十分连续光滑,没有明显的波动和干扰,可见基于稳态电流法的实验效果良好,系统误差源被有效地抑制。根据所得转矩曲线可知,该实验所测得的转矩特性与开关磁阻电动机的基本理论相符合[8-9]。
2 基于解析法的转矩特性数学建模
在测得转矩特性之后便可通过查表的方式得到特定电流和位置所对应的转矩大小,然而实验法所得转矩数据存在一定的局限性。一方面,实验法得到的均是离散数据,不能精确定位到任意位置、任意电流所对应的转矩,难以满足控制精度较高的场合。另一方面,在实际应用中查表的方式也将大量消耗控制器的资源。虽然可以通过减小实验的步距角增加实验次数来提高精度,但这对实验仪器有着严苛的精度要求,也将耗费更多的人力物力。因此连续的转矩-电流-位置的函数关系对于高精度的开关磁阻电动机控制至关重要,这需要得到转矩特性的解析表达式[10]。然而开关磁阻电动机的高度非线性导致没有现有的物理公式来描述这3 个变量间的非线性耦合关系,因此要得到转矩特性的解析函数,需要基于转矩的实测数据,通过曲线拟合的方式得到一个经验公式来近似。
2.1 基于最小二乘拟合的转矩模型
转矩特性的曲线拟合需要先拟合出各电流对应的转矩T 关于位置角θ 的函数T(θ,P)(其中P 为拟合系数),再拟合出各转子位置对应的P 关于电流i 的系数函数P(i),从而得到转矩的解析函数T(θ,P(i)),即T(θ,i)。本研究以实测转矩数据为基础,使用最小二乘法分别尝试了7 ~12 阶多项式的曲线拟合,拟合效果如图7所示,拟合的精度指标如表2所示。
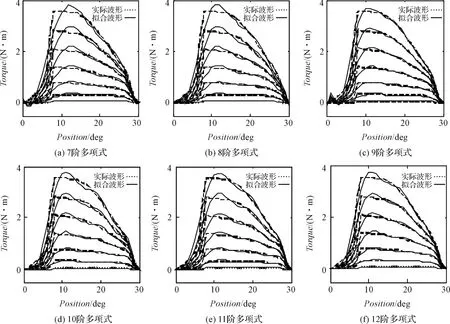
图7 不同阶数下转矩的多项式拟合效果
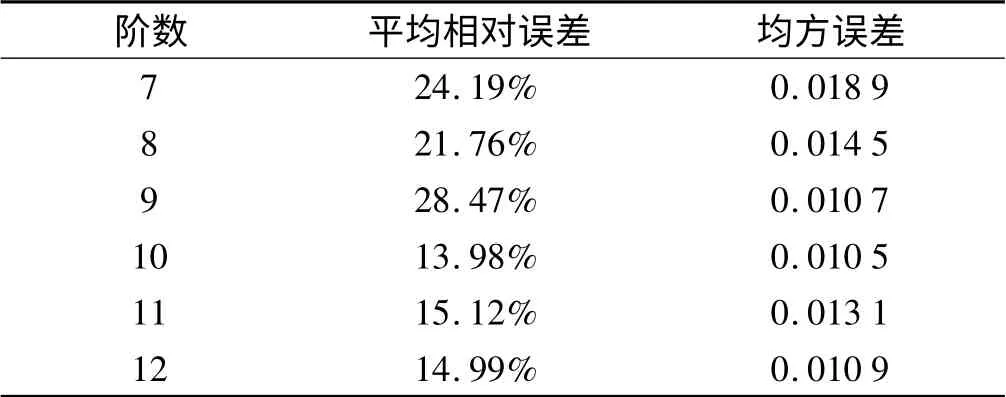
表2 不同阶数对应的拟合精度指标
从波形中可以看出,9 阶多项式在后半区间内的拟合效果最为平滑稳定,曲线的波动程度最小,但其在小角度区间上的明显波动影响了整体的拟合效果,故其平均相对误差最大,达到了28.47%。按照最小二乘法的原则,应选择均方误差最小的10 阶多项式作为拟合函数,然而在得到多项式系数后还需将各多项式系数对电流再一次进行拟合,每增加一个多项式系数便增加一次曲线拟合,这就增加了整体的计算复杂度。因此在考虑均方误差和平均相对误差的同时还需权衡整体的拟合难度,应尽量减少拟合函数的多项式系数。各阶多项式拟合结果中,12 阶多项式从4 次方项到常数项的多项式系数均为0,因此实际的系数为8 个,在各阶多项式拟合结果中个数最少。与此同时,12 阶多项式拟合的平均相对误差和均方误差分别为14.99%与0.010 9,与9 阶多项式的对应精度指标仅有微小差别,因此本研究选择12 阶多项式作为拟合函数,即:
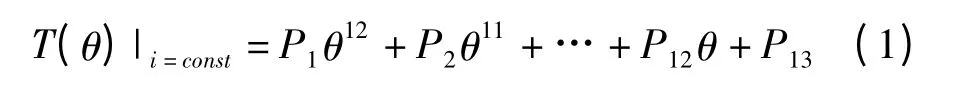
以式(1)作为转矩的拟合函数,分别对电流为1 A ~7 A时所对应的7 组转矩-角度特性进行拟合,可得7组多项式系数。由于P9~P13均为零,实际的转矩函数如下式:
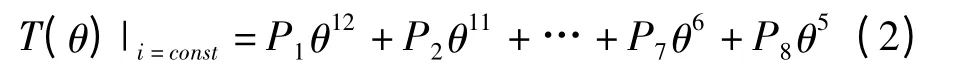
得到各电流对应的多项式系数P1~P8后,还需对各系数Pi(i =1 ~8)再进行一次关于电流的拟合,以得到最终的转矩函数,即:
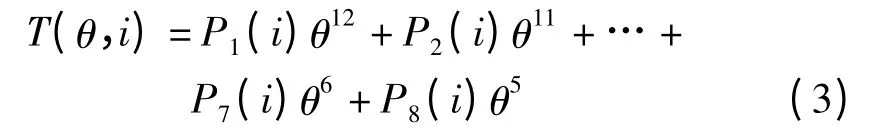
经试验,5 阶多项式拟合的结果精度较高,这将会产生新的8 组多项式系数,将各组多项式系数分别代入其对应多项式函数即可得到要求的8 个多项式系数函数P1(i)~P8(i)。最后将P1(i)~P8(i)代入式(3)便得到了最终的转矩拟合函数T(θ,i),其对应的二维曲线及其整个周期的三维曲面如图8所示。拟合的总体平均相对误差为14.89%,均方误差为0.011 0。由此便完成了转矩特性解析模型的建立。
2.2 基于区间分段的转矩拟合模型
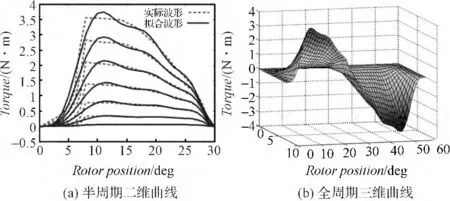
图8 转矩特性的解析模型
转矩函数的平均相对误差达到了14.89%,与实际转矩特性已经有了较为明显的误差。这是由于转矩函数的波形具有强烈的非线性,难以找到能反映其变化规律的基本初等函数作为拟合函数。与此同时,转矩波形在其周期内的单调性也有变化,在前三分之一周期内为增函数,后三分之二周期内为减函数,且转矩增加的速度很快,减少的趋势却较为平缓,中间还有一段接近水平的区域。若使用同一种函数来进行拟合,对转矩特性的跟踪将顾此失彼,难以同时准确地拟合出两种相反的变化趋势。因此本研究将针对此问题对转矩特性以分段的方法进行拟合,也就是将拟合的区间从转矩增减性发生改变的位置附近分开成两个单调区间,前半区间为增区间,后半区间为减区间。然后再分别对这两个单调区间上的转矩特性进行拟合,分别得出两个区间上的解析函数,最后通过分段函数的形式给出转矩特性的解析函数。
由转矩的实测波形可知,从非对齐位置到8°位置附近的区间内转矩单调增加,其后到对齐位置的区间内转矩单调减少,因此本研究首先以8°位置为分界点,将角度区间分为增区间和减区间两个部分。与此同时将转矩的实测数据也以8°为分界点分前、后两个部分,并依此数据为基础,分别对增减区间的转矩数据进行拟合。拟合仍然采用最小二乘的方法,并以多项式函数作为拟合函数。经试验,增、减区间的拟合函数分别选取7 阶多项式和5 阶多项式可以得到较高的拟合精度,其拟合效果图如图9所示。
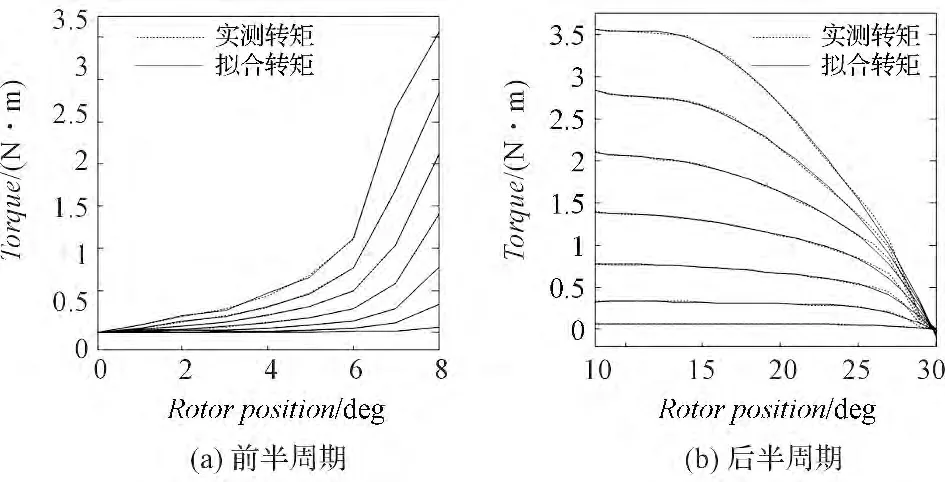
图9 使用分段法所得转矩特性的拟合效果
增区间和减区间所对应的拟合转矩和实际的对比图如图9(a)、9(b)所示。从图中可以明显看出采用分段的方法拟合转矩较为精确地跟踪了实测转矩,前半区间与后半区间的总体平均相对误差减小到了3.61%,均方误差减小到了5.82 ×10-4。因此对于从非对齐位置到对齐位置的完整区间,固定电流的转矩-角度的解析函数是一个以8°为分段点的分段函数,两个区间上都为多项式函数,阶数分别为7 阶和5 阶,即:
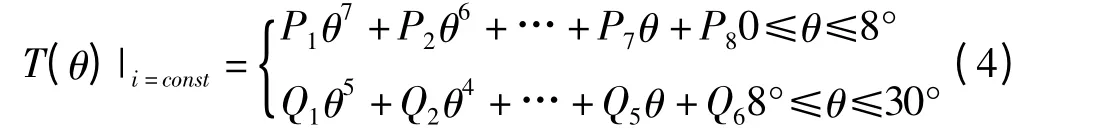
式中:P1~P8—增区间转矩函数的多项式系数;Q1~Q6—减区间转矩函数的多项式系数。与完整区间上的转矩拟合一样,此时需要进一步完成各多项式系数对电流的拟合,以得到各多项式系数关于电流的函数,并最终求出转矩关于角度和电流的二元函数,即:
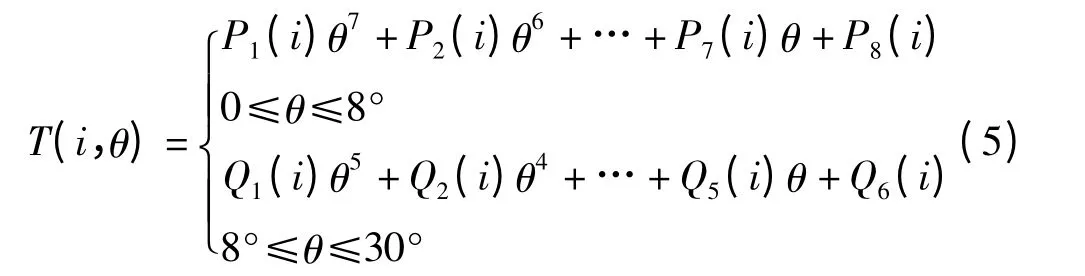
经试验,前、后半周期均采用7 阶多项式可达最佳拟合精度效果。将拟合所得关于电流的多项式系数分别代入前、后半周期的各多项式函数,便得前半周期的多项式系数函数P1(i)~P8(i)以及后半周期的多项式系数函数Q1(i)~Q6(i)。最后分别将式P1(i)~P8(i)和式Q1(i)~Q6(i)代入式(5),便得到了使用区间分段拟合法的解析函数。现在本研究根据解析函数绘制出整个周期的转矩拟合曲线和转矩实测曲线的二维曲线,以及经对称化处理后的转矩三维曲面图形,分段拟合法的转矩曲线及转矩曲面如图10所示。
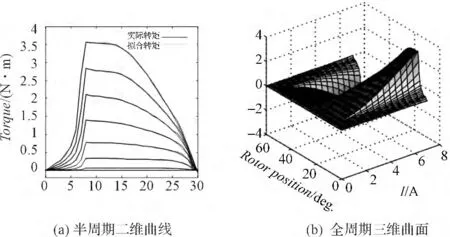
图10 分段拟合法的转矩曲线及转矩曲面虚线为实测转矩,实线为拟合转矩
从图中可以看出使用分段的方法后拟合转矩对实测转矩的拟合效果较为理想,从图像中已难看出明显误差。拟合的平均相对误差为6.14%,均方误差为0.024 5,精度较高。因此,使用基于区间分段拟合法的效果要明显好于完全区间拟合法。
3 结束语
本研究针对开关磁阻电动机转矩特性难以获取的问题,首先分别用基于暂态电流和稳态电流的方法对一台4 相8/6 极开关磁阻电动机进行了转矩测量实验,其中使用稳态电流法所测得转矩精度较高;接着在实验测得的转矩数据的基础上,对实验样机的转矩特性进行了数学建模。建模主要使用基于最小二乘的曲线拟合方法,得到了实验样机转矩关于相电流和转子位置角的函数解析式。
同时,本研究还提出了一种区间分段拟合的方法,提高了拟合精度。
[1]KRISHNAN R.Switched Reluctance Motor Drives[M].Florida:CRC Press,2001.
[2]GOBBI R,SAHOO N C,VEJIAN R R.Rising and Falling Current Methods for Measurement of Flux-Linkage Characteristics of Switched Reluctance Motors:A Comparative Study[C].2006 First IEEE International Power and Energy Conference,Putra Jaya,Malaysia,2006:383-387.
[3]TORREY D A,LANG J H.Modeling a nonlinear variable reluctance motor drive[J].Electric Power Applications,IEE Proceedings B,1990,137(5):314-326.
[4]FUENGWARODSAKUL N H,BAUER S,TSAFAK O,et al.Characteristic Measurement System for Automotive Class Switched Reluctance Machines[C].2005 IEEE 11th European Conference on Power Electronics and Applications,Dresden,Germany,2005:1-10.
[5]ZHANG Peng,CASSANI P A,WILLIAMSON S S.An accurate inductance profile measurement technique for switched reluctance machines[J].IEEE Transactions on Industrial Electronics,2010,57(9):2972-2979.
[6]宋小川,王家军.开关磁阻电动机的一种磁链建模方法研究[J].机电工程,2014,31(11):1426-1430.
[7]GOBBI R,SAHOO N C,VEJIAN R.Experimental investigations on computer-based methods for determination of static electromagnetic characteristics of switched reluctance motors[J].IEEE Transactions on instrumentation and measurement,2008,57(10):2196-2211.
[8]MILLER T J E.Switched Reluctance Motors and Their Control[M].Oxford:Magna Physics Publishing and Clarendon Press,1993.
[9]MILLER T J E.Electronic Control of Switched Reluctance Machines[M].Oxford:Newnes Press,2001.
[10]VUJICIC V P.Modeling of a switched reluctance machine based on the invertible torque function[J].IEEE Transactions on Magnetics,2008,44(9):2186-2194.

