冗余驱动并联摇摆台的动平台刚度分析

孙巧如，韩先国

（北京航空航天大学 机械工程及自动化学院，北京 100191）

0 引言

并联机构具有刚度质量比大、承载能力强、累积误差小等优点[1]，将其作为运动模拟器模拟船舶在海浪中的运动具有重要的意义。其动平台具有尺寸大、承载能力要求高、刚度要求高等特点，因此采用冗余驱动提高系统刚度[2]。

国内外学者在并联机构的刚度方面进行了一定的研究。梁辉等[3]通过建立3RPS/UPS 冗余并联机床的刚度模型对并联机床的支链进行刚度分析，Goldsmith[4]应用刚度矩阵分析法建立3-UPU 并联机构的刚度解析模型，宋轶民等[5]采用螺旋理论建立了一种三自由度冗余驱动并联机构的刚度解析模型，并预估其全域刚度分布规律。现有文献对并联机构的刚度进行了一定的研究，但是多数将并联机构的动平台视为理想刚体，并未对其刚度进行分析。针对本文所设计的并联摇摆台，由于其动平台的尺寸大、刚度要求高，因此需要对其刚度进行一定的研究。

利用有限元分析机构的刚度方法简单，精度较高，但是耗时多，工作量大，为便于并联机构参数的多变量优化设计，仍需要建立机构的静刚度解析模型。首先，根据并联摇摆台动平台的特点，将其简化为交叉梁系，针对并联机构在非冗余驱动和冗余驱动时的不同特点，将交叉梁系合理地拆分为简支梁，采用节点载荷分配系数法将节点上的载荷分配给相交的各梁，根据同一节点处变形量相等的条件，建立关于各节点载荷分配系数的方程，进而计算出动平台在非冗余驱动和冗余驱动时的理论最大变形量，并对其进行比较。然后，采用有限元分析的方法计算动平台的最大变形量，与理论计算结果进行对比。最后，说明冗余驱动存在驱动误差时，系统可以通过动平台自身刚度的变化减小由于驱动误差而导致的内力耦合。

1 3UPS/U 并联机构介绍

3UPS/U 并联机构由动平台、静平台、驱动支链和中间立柱组成。驱动支链上端通过球铰与动平台连接、下端通过虎克铰与静平台连接，中间立柱上端通过虎克铰和动平台连接，下端固定在动平台上，通过控制驱动支链的长度变化实现动平台的运动。动平台在驱动支链和中间立柱的共同作用下具有两个转动自由度，驱动支链的数目为3，大于机构的自由度数目，因此，机构属于冗余驱动并联机构。该并联机构的动平台尺寸大、刚度要求高，因此其骨架采用箱梁结构，相互之间成井字形布置。

2 动平台骨架刚度分析

为了对动平台的骨架进行刚度分析，将动平台骨架简化为如图1 所示的空间交叉梁系，首先分析动平台骨架在非冗余驱动时的刚度情况。在动平台骨架所受载荷不变的情况下，其刚度的大小即表现为变形量的大小。

图1 中，A、B、C 分别为驱动支链、中间立柱与动平台的连接点，以C 点为坐标原点建立C-XY 坐标系，规定沿X 轴方向的梁为横梁，即横梁1、2、3、4、5，沿Y轴方向的梁为纵梁，即纵梁a、b、c、d、e、f、g、h，梁的节点坐标用横、纵梁的标号表示，即节点1a、2b、3b 等。

由于外伸梁的挠度可以根据材料力学[6]中的叠加法以及位移合成法计算得到，而空间交叉梁系的各个梁之间由于共用结点而相互影响，因此，不能直接计算出交叉梁系的变形量。为了得到交叉梁系的变形量，需要将复杂的空间交叉梁系通过一定的方法简化为简单的外伸梁。文献[7]以荷载分配系数为未知量，将作用在交叉梁系节点上的荷载按照分配系数分配给在节点相交的各梁，从而将交叉梁系拆分为一根根单一的简支梁来计算。但是文献中所讨论的交叉梁系的约束位置都位于梁系的边缘，因此可以按照横梁和纵梁的方式拆分梁系的结构，而在本文所述动平台的骨架结构中，交叉梁系所受到的约束位于梁系的内部节点上，因此不能简单地将梁系划分为横梁和纵梁两部分，而要根据约束的位置，合理地拆分梁系的结构，保证拆分后的结构在计算节点变形时比较方便。根据本文中交叉梁系的结构以及梁系受到的约束，将梁系划分为如图1 所示的两部分，虚线部分和实线部分，有跨线的地方表示此节点处的横梁和纵梁是相互独立的，相交的部分表示此节点处横梁和纵梁是相连的。

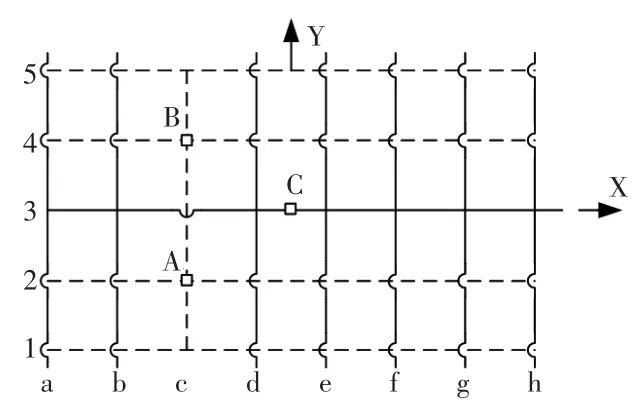
图1 空间交叉梁系示意图Fig.1 The schematic diagram of space intersection beam systems

假设梁系受到的载荷为均布载荷q，首先将均布载荷转化为节点处的集中载荷Q，每一个节点处的载荷分别由相交于此节点的横梁和纵梁承担。设μix、μiy分别为同一节点处横梁和纵梁上的载荷分配系数，μix+μiy=1，那么节点处的载荷分配给横梁和纵梁的值分别为μixQ、μiyQ。

根据拆分后的梁系结构，分别计算每个节点在横梁和纵梁中的变形量，根据同一节点处变形量相等的条件，得到关于每个节点的载荷分配系数μix和μiy的方程，解方程可以求得μix和μiy，将其反代入节点的变形量方程中，即可求得各结点的变形量，进而可求得交叉梁系的刚度。

2.1 横梁上各节点的变形

拆分后的横梁结构如图2 所示，B、C 为此梁系的约束位置。由于实际梁系结构的扭转变形相对于弯曲变形比较小，因此此处忽略扭转变形。

以节点1h 为例来说明求解节点变形量的原理。节点1h位于横梁1 上，横梁1 通过节点1c 和支撑A、B 相连，为了得到节点1h 的变形量，首先需要计算节点1c 的变形量，节点1c 处的挠度为δ1c。

由于在节点1c 处横梁1 和纵梁c 为刚性连接，因此单独分析横梁1 的变形时可以把节点1c 看作是固定端，根据梁变形的叠加法可知，在横梁1 上各个节点力的作用下，横梁1 上节点1h 的变形量为

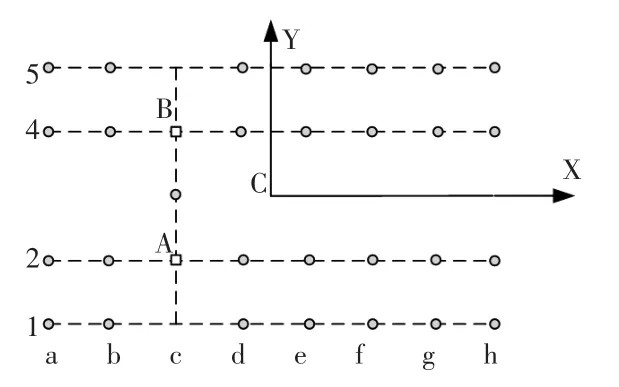
图2 拆分后的横梁结构Fig.2 The structure of beam after separation

横梁1 上节点1h 的总的变形量包括悬臂梁1 计算得到的1h 的变形量与固定端1c 处的变形量之和，因此，横梁1 上节点1h 的总的变形量为：只与μix（i=a，b，d，e，f，g，h）、μ3cy有关。同理，可以得到横梁结构中其它各节点的变形量。

2.2 纵梁上各节点的变形量

拆分后的纵梁结构如图3 所示，由于纵梁h 所在的梁系结构只有一个铰支座约束C，结构属于欠约束结构，因此需要寻找其他合适的约束条件，使拆分出来的梁系结构达到稳定状态。根据横梁1 所在的梁系结构的计算结果可知，节点3c 的变形结果已知，设为μ3cy，那么可以将节点3c 当作具有一定位移的铰支座。由于节点3c 具有一定的位移，因此横梁3 在支座C 处具有一定的转角θ，但是由于μ3cy/（1.5L）≈0，因此，可以近似认为横梁3 不受铰支座3c 的位移的影响。

同理，以节点1h为例来说明求解节点变形量的原理。节点1h 位于纵梁h 上，纵梁h 通过节点3h 和支撑C、3c 连接，因此为了得到节点1h 的变形量，首先需要计算节点3h 的变形量，节点3h 处的挠度为δ3h。

单独计算纵梁h 上节点1h 的变形量时，可以把节点3h 看作是固定端，那么纵梁h 的下半部即为悬臂梁，根据悬臂梁的挠度计算公式以及叠加法可知，纵梁h 中节点1h 的变形量为纵梁h 上节点1h 的变形量为：只与有关。同理，可以得到纵梁结构中其它各节点的变形量。

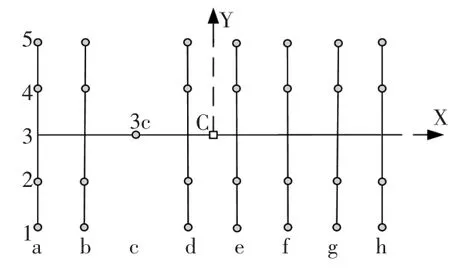
图3 拆分后的纵梁结构Fig.3 The structure of beam after separation

3 计算实例

由于原模型比较复杂，需要计算位移的节点数量比较多，因此，采用一个与原模型类似、但比较简单的模型来验证此方法的正确性。

采用上述方法分别计算节点1a、2a、1c、2c、1d、2d 在X 向梁上的变形量和在Y 向梁上的变形量，使二者相等，可以得到：

采用有限元软件分析得到冗余驱动时交叉梁系的变形情况如图5 所示。有限元分析的结果为0.13416mm，误差为：

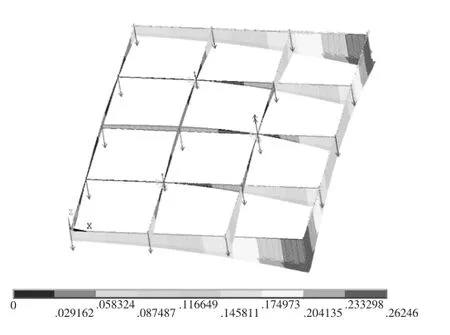
图4 非冗余驱动时交叉梁系变形情况Fig.4 Deformation of space intersection beam systems with non-redundant

图5 冗余驱动时交叉梁系变形情况Fig.5 Deformation of space intersection beam systems with redundant

理论计算得到交叉梁系的最大变形量基本与有限元软件分析得到的最大变形量一致，表明采用载荷系数分配法计算交叉梁系的变形量的方法是可行的。

比较非冗余驱动时交叉梁系的最大变形量和冗余驱动时交叉梁系的最大变形量可得，增加冗余驱动后，动平台骨架的最大变形量减小了55.2%。

4 动平台刚度变化对驱动误差的影响

动平台的刚度不仅与自身结构有关，还与驱动支链的数量和布置位置有关。并联摇摆台采用冗余驱动时，当冗余驱动出现驱动误差时，若动平台为纯刚体，由于各驱动支链之间的内力耦合，会使系统产生较大的内力，甚至导致系统结构破坏；当动平台的刚度较小时，可以通过动平台自身刚度的变化减小由于驱动误差而产生的系统内力耦合，避免出现结构破坏。

假设冗余驱动支链由于驱动误差而产生的位移为△d，若动平台为纯刚体，那么由于冗余驱动支链的驱动误差而导致的其它驱动支链的变形为△D，若动平台的刚度较小，那么由于冗余驱动支链的误差而导致的其它驱动支链的变形为△D-δd，δd 为动平台上对应驱动支链处的节点变形量。因此冗余驱动支链的驱动误差对其它驱动支链的影响可以通过动平台自身刚度的变化而减小，即各支链之间的耦合内力会相应地减小。

5 结论

本文通过将并联机构的动平台的骨架简化为交叉梁系，介绍了采用载荷分配系数法计算交叉梁系变形量的原理，并采用有限元软件对其计算结果进行验证，得到： ①根据交叉梁系结构和所受约束，采用载荷分配系数法合理地拆分并计算各结节点变形量的方法是可行的；②从理论上说明了冗余驱动对于提高并联机构动平台刚度起到了重要作用；③当冗余驱动存在误差时，可以通过动平台自身刚度的变化减小由于冗余驱动误差而导致的系统内力耦合。

[1] 黄真，孔令富.并联机器人机构学理论及控制[M].北京: 机械工业出版社，1997.

[2] Liu G F，Wu Y L. Analysis and control of redundant parallelmanipulators[A].Proceedings of the 2001 IEEE International Conference on Robotics & Automation[C]. 2001.

[3] 梁辉, 白志富. 具有内力的3RPS/UPS 冗余并联机床刚度分析[J].机械设计，2007，1.

[4] Goldsmith P B. Design and kinematics of a three-leggedparallel manipulator[J].IEEE Transactions on Roboticsand Automation，2003，4.

[5] 宋轶民，翟学东. 一种三自由度冗余驱动并联模块的刚度分析[J].天津大学学报，2015，1.

[6] 同济大学航空航天与力学学院基础力学教学研究部. 材料力学[M]. 上海：同济大学出版社，2005.

[7] 张定华. 空间平板网架交叉梁系的荷载分配法[J].贵州工学院学报，1987.