基于Morlet小波变换的振动特性参数识别
张济民,周俊华,王开文,陶建兰
(1.同济大学铁道与城市轨道交通研究院,上海201804;2.西南交通大学牵引动力国家重点实验室,四川成都610031;3.同济大学经济与管理学院,上海200092)
式中:w(a,b)为小波变换系数;〈f(t),Ψa,b(t)〉代表f(t)和Ψa,b(t)的内积,a,b分别为尺度因子和平移因子;Ψ*为母小波函数的复共轭.本文应用著名的Morlet小波作为母小波函数,Morlet小波是高斯包络下的复指数函数,其虚部是实部的Hilbert变换,解析表达式如下:
基于Morlet小波变换的振动特性参数识别
张济民1,周俊华1,王开文2,陶建兰3
(1.同济大学铁道与城市轨道交通研究院,上海201804;2.西南交通大学牵引动力国家重点实验室,四川成都610031;3.同济大学经济与管理学院,上海200092)
传统的振动系统特性参数识别方法对于非线性、非平稳信号的处理能力差,尤其对于阻尼比的识别精度较低.将Morlet小波变换和随机减量技术相结合识别振动系统的特性参数,首先利用随机减量技术提取振动的自由衰减响应信号,进而由Morlet小波变换对信号进行连续的小波变换处理得到小波能量谱,结合参数识别的基本理论及对时间-幅值坐标面曲线的半对数拟合结果得到振动系统的频率及阻尼比,数值仿真结果表明,提出的方法能有效识别系统的固有频率和阻尼比.将该方法应用于罐车模型流固耦合冲击试验研究,较好地识别出充液工况下振动系统的固有频率和阻尼比.
Morlet小波变换;随机减量技术(RDT);振动特性参数;流固耦合冲击试验;阻尼比
在振动分析中,系统的振动特性参数包括固有频率及阻尼比的准确识别是一项十分重要的任务.由于随机减量技术实现简单、高效灵活,同时在实际工况下可以实现数据实时分析,现在已经成为一项提取结构自由衰减信号的有效方法,并且在振动模态分析、结构损伤检测等领域中得到广泛的应用[1].而小波变换(wavelet transformation,WT)以其自适应的时频域分辨率变化的特征成为研究非线性和非平稳数据的重要工具,其克服了传统傅里叶变换无法在时域局部化的缺陷,改变了短时傅里叶变换的固定时频分辨率的状况,通过小波函数与信号的匹配机制揭示信号的瞬时特征[2].近年来,随着小波理论的日益成熟,针对小波变换用于参数识别的研究前人已经做了一些重要的工作[3-5],取得了较大进展.
鉴于考虑流固耦合振动的频率及阻尼比参数识别的研究较少,本文基于随机减量技术(random decrement technique,RDT)和Morlet小波变换相结合的这种实用的参数时频域识别方法将其应用到罐车模型流固耦合试验研究中.首先利用随机减量技术对实测的加速度数据处理提取出自由衰减响应,进而由以Morlet小波为母小波函数的连续小波变换处理得到三维小波能量谱,结合参数识别的基本理论及对时间 幅值坐标面曲线的半对数拟合得到固有频率和阻尼比.
1 随机减量技术
随机减量技术是一种从结构的随机响应信号中提取该结构自由衰减信号的处理方法,其基本思想为指定某种条件,将随机响应信号中确定性的和随机的两部分实现分离,然后利用统计平均将随机的部分排除掉,过滤出确定性的自由衰减信号.
对线性系统来说,任意激励下的受迫振动响应方程可表示为

式中:y(t)为系统振动位移,t为时间;D(t)为初始位移为1且初始速度为零的系统自由响应;V(t)为初始位移为零且初始速度为1下的系统自由响应;y(0)和y·(0)分别为系统振动的初始位移和初始速度;h(t)为系统的单位脉冲响应函数;f(t)为外部激励;τ为任一时刻.
选取一个适当的常数去截取该系统的振动响应信号y(t),可得到一系列不同的交点时刻ti(i=1,2,…,N),对于自ti时刻开始的响应y(t-ti)可表示为

将y(t-ti)的一系列时间ti起始点移至坐标原点,可获得相应的一系列时移后的函数xi(i=1,2,…,N),取xi(t)的统计平均,得
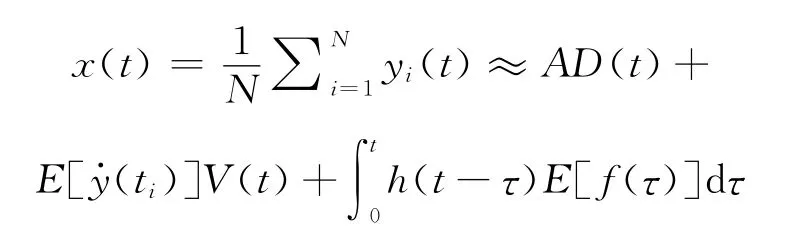
式中:A为初位移;E[f(t)]为外部激励的均值.
f(t)若是平稳的随机激励且均值为零,则系统振动响应y(t),y·(t)同样是均值为零的平稳随机过程,即有E[f(t)]=0,E[y·(ti)]=0,则
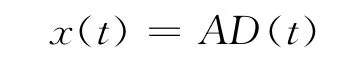
式中:x(t)为初位移为A、初速度为零的自由振动响应.
2 Morlet小波变换
小波变换的基本思想是先选择一个满足条件的母小波,对其进行平移和伸缩,得到一组小波基,再利用这组小波基去表示和逼近信号,从而可以对信号进行时频局部化分析.小波变换的本质就是将信号用一系列有限基函数进行表示,展现采用正交基的传统傅里叶分析所不能表示的信号瞬态特性.对于任意信号f(t)∈L2(R),其连续小波变换(continuous wavelet transform,CWT)可表示为

式中:w(a,b)为小波变换系数;〈f(t),Ψa,b(t)〉代表f(t)和Ψa,b(t)的内积,a,b分别为尺度因子和平移因子;Ψ*为母小波函数的复共轭.本文应用著名的Morlet小波作为母小波函数,Morlet小波是高斯包络下的复指数函数,其虚部是实部的Hilbert变换,解析表达式如下:

式中:ω0为小波的中心频率.其傅里叶变换为

在频域中,信号的连续小波变换可以通过变换得到
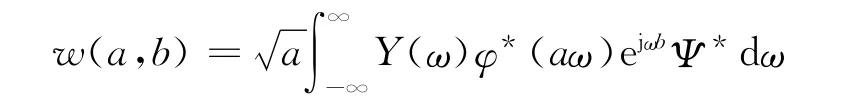
式中:Y(ω)和φ*(aω)ejωb分别是信号f(t)和母小波函数
的傅里叶变换.
上述式子可以表述为离散形式
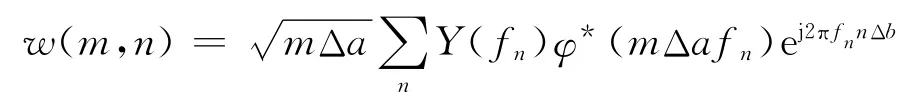
式中:fn是离散频率.
3 阻尼比识别
3.1 阻尼比识别原理
文献[6]基于改进Morlet小波变换的模态识别方法识别了密集模态取得良好效果,并通过三自由度的仿真算例表明基于Morlet小波变换能以较高精度识别系统的阻尼比等模态参数;文献[7]提出自然激励法与复小波变换相结合的模态参数识别方法;文献[2]基于Gabor小波函数的解析小波变换通过小波函数与复值信号的匹配机制揭示信号的幅频和相频信息以实现结构模态阻尼参数的识别;文献[8]同时采用了Hilbert变换和Morlet小波变换对自由振动下的动态响应信号进行包络的提取实现了金属橡胶干摩擦系统的阻尼识别.其他文献[9-12]有类似基于参数化小波变换的阻尼识别,证明了小波变换对阻尼比的辨识作用.
对于单自由度或者多自由度的线性系统来说,其动力学模型可以表示为

式中:M,C,K分别为多自由度系统的质量矩阵、阻尼矩阵和刚度矩阵,对于单自由度系统,M,C,K分中只有1个元素;F为激励变量;Y为系统响应.
自由系统的单程黏性阻尼的脉冲响应是
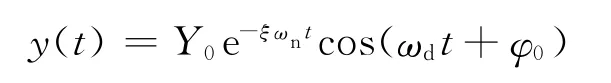
式中:ωn为系统的无阻尼固有圆频率;ωd为有阻尼固有圆频率,ωd=ωn,ξ为阻尼比;φ0为初始角.函数A(t)=Y0e-ξωnt为缓慢变化且脉冲响应适用于选定的小波变换.

式中:φ(t)为傅里叶变换.上述式子的模表示为

当a确定,例如a=ai(i=1,2,…,M)(ai为常数).从上述式子可以推出

对等式取对数,有

因此,系统的阻尼比ξ可以从连续小波变换时间-频率坐标面曲线的斜率拟合得到,ai绘制在半对数刻度中.
单自由度的阻尼比小波变换估计方法可扩展到多自由度系统中,多自由度系统的小波分解响应是

式中:ωnj,ωdj和ξj分别为系统每阶的无阻尼固有圆频率、有阻尼固有圆频率和阻尼比,j为系统的振动阶次数
3.2 数值仿真
构造一个二自由度振动系统的自由振动信号

式中:A1=1.0,A2=0.8,ξ1=0.010,ξ2=0.005, ω1=4π,ω2=8π,θi=0,ωdi=ωi采样频率为100Hz,采样时间为30s.
图1为所构造的二自由度振动系统的自由振动信号,对其进行连续小波变换,得到三维的小波能量谱,如图2所示.对处理得到的固有频率下的时间幅值坐标面对曲线进行半对数刻度化及曲线线性拟合,得到两固有频率下的阻尼比,列于表1.

图1 二自由度振动系统的自由振动信号Fig.1 Free vibration signal of vibration system with two degrees of freedom
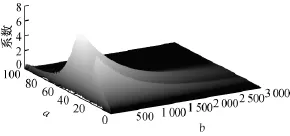
图2 自由振动信号的连续小波变换Fig.2 Continuous wavelet transform of free vibratioan signals

表1 频率与阻尼比识别结果Tab.1 The identification results of frequency and damping ratio
由表1可见,识别的两阶频率及阻尼比的误差都非常小,能够以非常高的精度识别出来.
4 基于加速度实测数据的罐车模型流固耦合振动特性参数识别
4.1 试验概况
选择国家自然科学基金项目中的罐车模型冲击试验所测得的纵向加速度数据进行处理,识别流固耦合振动下系统的振动特性参数.
试验车辆原型车为GJ70型液碱罐车,根据相似比例原理,对原型车的结构进行了部分简化.在保留主要部件的基础上(如底架装配、罐体装配和转向架等)简化了对研究分析无影响或影响较少的部件后得到试验所用1∶5比例罐车模型,如图3所示.加速度信号由安装在模型罐体、构架及车架上的加速度计测得.

图3 罐车模型纵向冲击试验Fig.3 Longitudinal impact test of tanker model
4.2 模型的频率及阻尼比识别
根据模型系统的特性和激励形式,选取罐车模型充液工况下车架实测数据作为研究对象,对该测点在纵向冲击下的纵向加速度响应信号进行处理和分析.图4为该测点的加速度响应时程曲线.利用RDT对该加速度信号进行处理,得到自由衰减响应信号,如图5所示.

图4 加速度信号的时间历程Fig.4 Time history of acceleration signals
对由RDT处理后得到的自由衰减信号(以下简称RD信号)进行连续小波变换,如图6所示,1~4 001的a值对应0.2~812.5Hz的频率区间,a值大小与频率大小成反比,其关系式为fj=f0(fs/fw)(1/aj),其中,fs和fw分别为信号的样本频率及小波的样本频率,f0为小波的中心频率.
RD信号的小波变换分析函数在固有频率fj时达到峰值,对图像进行处理可以得到系统的固有频率,列在表1中.取不同频率下的时间 幅值横截面进行分解,对该坐标面下的曲线进行半对数化处理及线性拟合,如图7所示.从拟合曲线可以看出,曲线斜率为-0.64,即在频率23.9Hz时的阻尼比为0.64%.不同固有频率下的阻尼比列于表2.
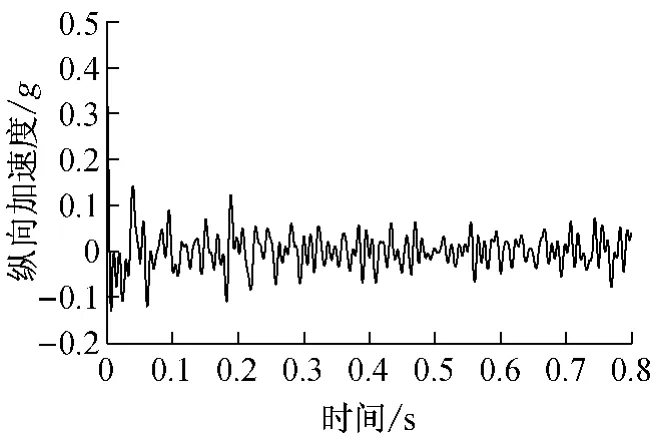
图5 利用随机减量技术得到的自由衰减信号Fig.5 The free decay signals after using the random decrement technique

图6 小波变换幅值Fig.6 The amplitude based on wavelet transform
5 结论
提出将随机减量技术和Morlet小波变换相结合用于罐车流固耦合振动系统的参数识别.在采用随机减量技术从振动信号中提取自由衰减信号的基础上,由Morlet小波函数进行连续的小波变换处理得到振动系统的特性参数.将该方法应用于处理罐车流固耦合冲击试验车架的纵向加速度实测数据,较好地辨识出其固有频率及阻尼比,与使用传统傅里叶变换方法识别出的参数也吻合,验证了该方法的可行性和有效性.该方法也可为一些振动系统参数识别的技术应用型工作提供参考及借鉴.
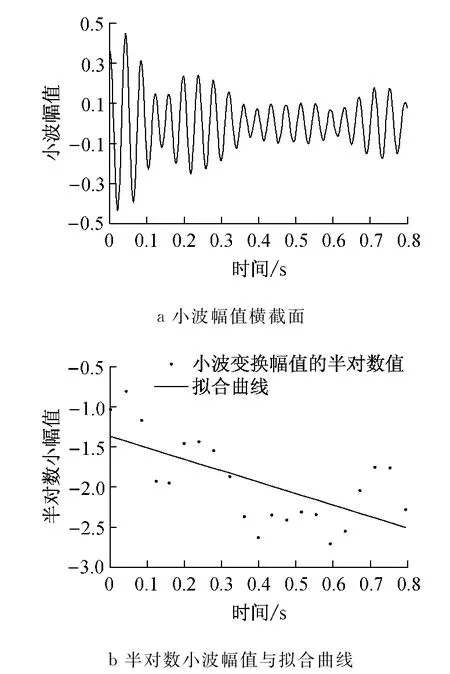
图7 RD信号在23.9Hz下的情形Fig.7 The result of RD signals at 23.9Hz

表2 基于小波变换后的频率及阻尼比Tab.2 The frequency and damping ratio after wavelet transform
[1] 黄琴,王彤,张海黎.基于随机减量的运行模态频域分析方法[J].南京航空航天大学学报,2011,43(06):770.HUANG Qin,WANG Tong,ZHANG Haili.Operational modal analysis method in frequency domain dased on random decrement[J].Journal of Nanjing University of Aeronautics &Astronautics,2011,43(6):770.
[2] 申建红,李春祥,李锦华.基于解析小波变换识别结构的模态阻尼参数[J].振动与冲击,2009(10):89. SHEN Jianhong,LI Chunxiang,LI Jinhua.Identifying structural modal damping parameters based on analytic wavelet transformation[J].Journal of Vibration and Shock,2009(10):89.
[3] Gomez-Luna E,Aponte Mayor G,Pleite Guerra J,et al.Application of wavelet transform to obtain the frequency response of a transformer from transient signals—Part 1:Theoretical analysis[J].IEEE Transactions on Power Delivery,2013,28(3):1709.
[4] Osofsky S S.Calculation of transient sinusoidal signal amplitudes using the Morlet wavelet[J].IEEE Transactions on Signal Processing,1999,47(12):3426.
[5] Lardies J,Gouttebroze S.Identification of modal parameters using the wavelet transform[J].International Journal of Mechanical Sciences,2002,44(11):2263.
[6] 罗光坤,张令弥.基于Morlet小波变换的模态参数识别研究[J].振动与冲击,2007(7):135.LUO Guangkun,ZHANG Lingmi.Study on identification of modal parameters based on Morlet wavelet transformation[J].Journal of Vibration and Shock,2007(7):135.
[7] 滕军,朱焰煌,周峰,等.基于复Morlet小波变换的大跨空间结构模态参数识别研究[J].振动与冲击,2009(8):25.TENG Jun,ZHU Yanhuang,ZHOU Feng,et al.Modal parameters identification of large span spatial structures based on complex morlet wavelet transform[J].Journal of Vibration and Shock,2009(8):25.
[8] 敖宏瑞,姜洪源,闫辉,等.基于小波变换的金属橡胶干摩擦系统阻尼识别[J].机械设计,2004(7):27.AO Hongrui,JIANG Hongyuan,YAN Hui,et al.Wavelet transformation based damping identificati on for metal rubber dry friction system[J].Journal of Machine Design,2004(7):27.
[9] 罗光坤.Morlet小波变换理论与应用研究及软件实现[D].南京:南京航空航天大学,2007.LUO Guangkun.A study on morlet wavelet transform theory and application with software implementation[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2007.
[10] 韩建平,李林,王洪涛,等.基于Hilbert Huang变换和随机减量技术的模态参数识别[J].世界地震工程,2011(1):72.HAN Jianping,LI Lin,WANG Hongtao,et al.Modal parameters identification based on Hilbert Huang transform and random decrement technique[J].World Earthquake Engineering,2011(1):72.
[11] 王超,朱宏平,王波.基于复小波变换的拉索结构阻尼比识别[J].华中科技大学学报:自然科学版,2012,40(7):115.WANG Chao,ZHU Hongping,WANG Bo.Identifying damping ratio of cable structures using complex wavelet transform[J].Journal of Huazhong University of Science and Technology:Natural Science Edition,2012,40(7):115.
[12] 王文芸.基于加速度响应信号连续小波变换的系统参数识别研究[D].南京:南京航空航天大学,2012.WANG Wenyun.Identification of structural parameters using the continuous wavelet transform of acceleration measurements[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2012.
Identification of Vibration Characteristics Parameters Based on Morlet Wavelet Transformation
ZHANG Jimin1,ZHOU Junhua1,WANG Kaiwen2,TAO Jianlan3
(1.Institute of Rail Transit,Tongji University,Shanghai 201804,China;2.Traction Power State Key Lab,Southwest Jiaotong University,Chengdu 610031,China;3.School of Economics and Management,Tongji University,Shanghai 200092,China)
Traditional identification methods of vibration system characteristics are not capable to process nonlinear and non-stationary signal,especially the low precision for identifying the damping ratio.An approach to identify the characteristics parameters of vibration system combining on random decrement technique and Morlet wavelet transform is proposed.Firstly,the free-decay vibration response signal was extracted by random decrement technique(RDT),and then signal was processed to give a continuous wavelet transform by the Morlet wavelet transform to get wavelet energy spectrum.Combined the basic theory of parameter identification and semi-logarithmic and curve fitting result in time-frequency coordinate plane,frequency and damping ratio of the vibrating system was got.The numerical simulation result that the proposed method can accurately estimate system natural frequencies and damping ratios.The method was applied for experimental study of tanker liquidsolid coupling model,the natural frequency and damping ratio of vibration system structure in loaded water conditions were well identified.
Morlet wavelet transform;random decrement technique(RDT);vibration characteristics parameters;impact experimental of tanker liquid-solid coupling model;dampingratio
TH113;U272.4
A
0253-374X(2015)12-1860-05
10.11908/j.issn.0253-374x.2015.12.014
2014 11 11
国家自然科学基金(61174214);“十二五”国家科技支撑计划(2012YQ15021307)
张济民(1969—),男,教授,工学博士,主要研究方向为车辆系统动力学及主动控制.E-mail:zjm397a@163.com
周俊华(1993—),男,工学硕士,主要研究方向为车辆系统动力学.E-mail:zjh6162@163.com

