一种水下无线传感器网络节点的三维部署算法*

赵敏华， 李玲燕， 赵 坤， 李 莉， 康燕妮

(1.西安建筑科技大学 信息与控制工程学院，陕西 西安 710055；2.中联西北工程设计研究院，陕西 西安 710082)

一种水下无线传感器网络节点的三维部署算法*

赵敏华1， 李玲燕1， 赵 坤1， 李 莉2， 康燕妮1

(1.西安建筑科技大学 信息与控制工程学院，陕西 西安 710055；2.中联西北工程设计研究院，陕西 西安 710082)

从水环境监测的应用需求出发，提出了水下空间节点三维部署的目标和约束条件。同时，为了解决在三层水下无线传感器网络结构模型下，节点稀疏部署后，网络存在的能耗不均衡问题，提出一种非均匀简单立方格节点部署算法。该算法结合节点水声通信能耗模型，通过增加各层节点数目和调整节点间通信距离来控制节点能耗。从网络的生存时间和网络的能量消耗两方面对算法进行了分析和仿真，结果表明:本算法可以在保证网络覆盖要求的前提下，控制节点部署的密度，均衡节点的能量消耗，延长网络寿命。

水下无线传感器网络； 部署； 简单立方格； 通信能耗模型； 网络寿命

0 引 言

水下无线传感器网络(UWSNs)[1]是无线传感器网络(WSNs)领域新兴的研究热点。目前，国内外对UWSNs的研究主要集中在水声通信、UWSNs的体系设计、节点部署研究和网络通信的关键协议设计等方面。而水下节点的部署研究，由于其直接关系到网络监测信息的准确性、完整性和时效性，是众多研究方向的重中之首。合理的节点部署不仅可以节约节点资源，提高网络工作效率、优化网络资源，还可以均衡网络能耗，延长网络寿命。

与陆上WSNs相比，UWSNs具有许多不利于节点部署的特性，如水声传播速度小、水声信号传输损耗严重等[2]，这些特性大大提高了节点的部署难度。本文针对UWSNs在水环境监测领域的应用需求，设计了一种能耗均衡的UWSNs节点三维部署算法，该算法结合水下节点通信能耗模型，通过控制节点的输出功率来平衡网络能耗，可使网络在满足监测要求的前提下延长网络寿命。

1 问题描述

1.1 水下空间节点部署的目标

水环境监测应用要求网络具有规模大、成本低、网络生存时间长等特点。因此，网络的覆盖性能和网络的生存时间是网络布设时的主要目标。

1)连通性覆盖

由于水下通信环境的特殊性，适用于陆上传感器的覆盖即连通准则[3]不再适用于水下环境。同时，对于UWSNs，过多的冗余节点不仅会造成资源浪费，而且会造成通信干扰。因此，节点部署时应更注重网络的连通性覆盖。

2)网络生命周期

水下空间使得节点回收和能量补充较为困难，而水环境监测等应用却要求网络能长时间生存，因此，在布设节点时，应充分考虑各个节点的能量开销问题，充分延长网络的生命周期。

1.2 水下空间节点部署的约束条件

1)水下节点造价高

单个水下无线传感器节点需要配备水声调制解调器、大容量电池和节点固定装置，致使成本昂贵。

2)网络能耗不均衡

在数据传输时，水下节点采集到的数据最终要被转发到水面节点，则距离水面节点较近的水下节点，其处理的信息流远大于更深处的节点。而通信能耗又是传感器节点最主要的能耗单元[4]。因此，离水面越近的节点将越早消耗完能量而死亡，导致网络生命期过早结束。

2 能耗均衡的节点部署算法

2.1 UWSNs结构模型

UWSNs结构模型采用三层模型，如图1所示。在第三层，水下传感器节点包括固定的水底节点和锚系方式悬浮在水中的悬浮节点，主要负责数据的收集、融合、转发等，具有位置固定，计算、存储资源有限，能量不易补充，采用水声通信等特点。在第二层，位于水面的汇聚节点，负责收集第三层节点的数据，进行初步分析整合后通过短波、 卫星等多种通信技术上传到最上层的系统控制中心[5]。

图1 UWSNs三层结构模型Fig 1 Three layers structure model of UWSNs

2.2 水下节点感知模型

本文采用二元感知模型[6]来描述水下传感器节点的感知能力和作用半径。假设三维空间VS内传感器节点Si，其坐标为GSi(xi,yi,zi)，感知范围是以GSi(xi,yi,zi)为球心，RSi为半径的球体Bi。此时，空间VS中任意一点p(x,y,z)能被节点Si探测到的概率为

(1)

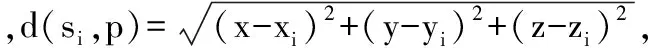
(2)

其中，nj为第j层被检测到的目标数，m为立方格总层数，N为总的目标数。

2.3 水声信道能量损失模型

水声信道是一个带宽有限、多途径效应干扰严重的时变、空变、频变的信道[8]。在水中，声波的传播损失TL主要由扩展损耗和衰减损耗两部分构成，即TL=10klgx+α(f)x[6]。其中,x为声波的传播距离，km；k为声波的传播因子(一般取值为1.5)，α(f)是吸收因子，可由Thorp经验公式计算得出[4]

α(f)=

(3)

当f单位为kHz时，α(f)的单位为dB/km。由传播损失TL可计算得到声波强度的衰减系数A(x)

(4)

那么，可得水声信道的能量损失模型为

(5)

其中，Pt为发送节点功率电平，Pr为接收节点接收功率，d为通信距离。可以看出，若Pr确定，则节点的发射功率由节点间的通信距离和发射频率决定。

2.4 节点通信能量消耗模型

水声信道能量损失模型只描述了信道的辐射能量损失情况，对于节点的能量消耗，还应包括组成网络节点的其他硬件设备的能耗。本文在分析节点的能量消耗时，主要考虑了节点通信系统的能耗，忽略了节点传感系统、控制系统和能源系统的能耗[2]。参考文献[9]，水声传感器网络节点通信单元的工作平均功耗可以表示为

(6)

其中，E0=Ptx(Ttx+Tsw)+Prx(Trx+Tsw)，b=P0Ttx。Mtx，Mrx为发送和接收单元每秒的工作次数；Ptx，Prx为发送和接收单元的平均功耗；Pout为输出功率，Tsw为切换时间，Ttx，Trx分别为发送和接收单元的工作时间[9]。从式中可看出，节点的通信能量消耗随通信距离的增加而指数次增加。

2.5 水下节点稀疏部署能量不均衡消耗分析

若UWSNs采用随机部署策略，为了较高的覆盖率，就需要布撒较多的节点，这大大地增加网络的运营成本。相对的，若UWSNs以稀疏方式进行确定性部署，则性价比较高。本文对稀疏部署方法中最直观的简单立方格结构进行能量消耗分析。在弱化节点在同层间的通信消耗后，采用链形网络来简化分析[10]，如图2所示。n个节点S={Si|i∈{1，……,n}}与一个Sink节点组成链形网络，链中任意两个节点相距l，每一节点只与离它最近的节点建立通信链路，水下节点通过多跳方式逐步传递到Sink节点。在这种结构下，可知越靠近水面Sink节点的水下节点，其传输的数据量越大，节点也会过早消亡。

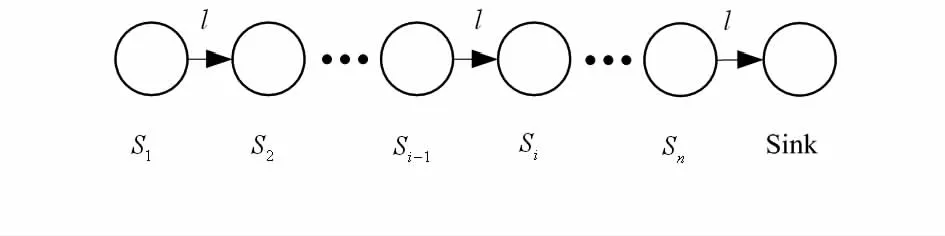
图2 单链路多跳拓扑结构Fig 2 Single link topology of multiple hop transmission

2.6 能耗均衡的节点部署算法

本文设计的节点部署算法是构建一个三维确定性稀疏部署结构，称为非均匀简单立方格结构。结构构建算法设定如下假设：1)水下节点的最大感知半径R是最大通信半径的1/3，此时网络符合覆盖即连通准则；2)水下节点位置固定，随水流移动距离忽略不计；3)节点处在休眠状态和运行状态转换时消耗的能量忽略不计；4)同层节点的通信半径相同。

算法具体步骤如下：

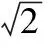
步骤2 双数层节点依照前一单数层进行部署。单数层节点依照一定方法减少该层节点的通信距离，并依据覆盖要求和通信距离确定是否增加节点数。

步骤3 定义一个最小感知半径为所有节点的感知半径下限。

步骤4 依照步骤逐层部署节点直至水面，水面的Sink节点采用均匀部署方式，确保水面下第一层的水下节点都能直接与Sink节点通信。

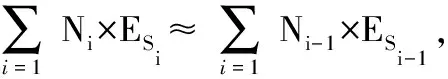
(7)

化简可得

(8)

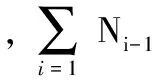
(9)

其中,j为整数。j值越大，每单数层需要的节点数成倍增加，这里，j=1。流程图如图3所示。

图3 算法流程图Fig 3 Flow chart of algorithm

3 仿真分析

3.1 仿真环境

本文采用Matlab进行仿真，从网络生命周期和网络能量消耗对本文算法的部署性能进行了分析。实验中的仿真参数设置如下：监测水域面积为1 000 m×1 000 m，深度为2 200 m；水下节点以UWM2000[11]为参考，设最大感知半径为250 m，最小感知半径为50 m，工作频率为35 kHz，初始能量为20 J，P0=1 W，k=1.5，Ptx=30 mW，Prx=20 mW，Ttx=Trx=0.1 s，Tsw=45 μs，当节点剩余能量小于0.01 J时，认为节点失效。图4显示了此时水下节点能量消耗与通信距离之间的关系，可以看出，随着节点传输距离的增加，节点的能量消耗大幅度增大。水面Sink节点的感知半径为350 m，节点数目为4个。

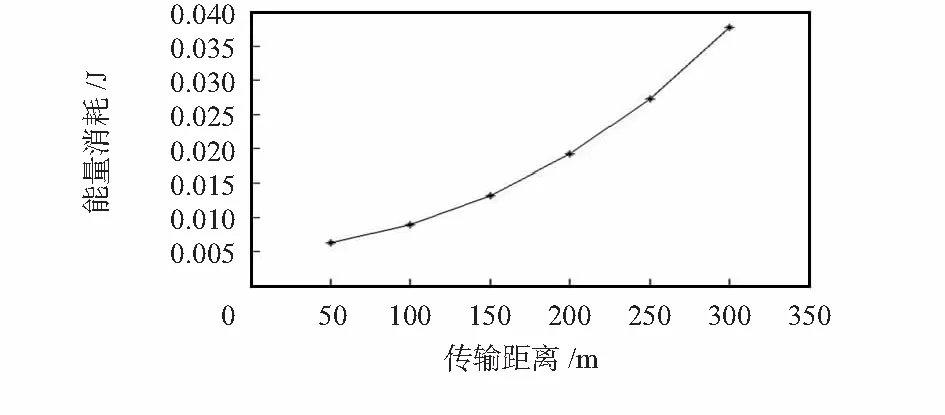
图4 水下节点能量消耗与通信距离之间的关系Fig 4 Relationship between energy consumption and communication distance of underwater nodes

3.2 非均匀简单立方格部署实现

依照本文算法，最终的部署结果如图5所示，为立方格内接球的球堆积形式，网络层数为7层，节点数为125个。

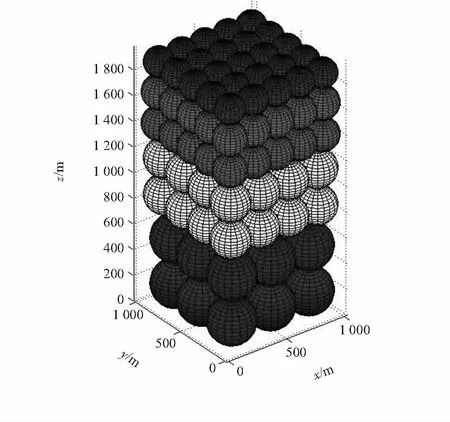
图5 最终部署结构Fig 5 Final deployment structure

为比较算法性能，在层数和节点数相同的条件下，任意设计两个初始目标覆盖率为1的稀疏部署结构。结构1：用125个节点对监测水域部署7层的均匀简单立方格结构，前6层每层节点数16个，后1层节点数29个，感知半径均为202 m；结构2：第1层节点数为11，感知半径为250 m，中间4层每层节点数为16，感知半径为210 m，后2层每层节点数为25，感知半径为154 m。

3.3 网络生存时间仿真分析

网络生存时间以轮数为单位，定义网络从运行开始到网络中第一个节点死亡的时间段为网络生命期。图6表明了本文算法和结构1、结构2的网络生存时间与剩余节点数目的关系。从图中可看出，在层数和节点数相同的初始条件下，本文部署算法从运行开始到第一个节点失效的时间>结构2>结构1，且相比结构2，本文算法的网络生命期提高了50 %。同时，随着发送数据轮数的增多，本文算法中失效的节点数目增长趋势平稳，且本文算法最终剩余的节点数量<结构1<结构2，说明本文算法较任意均匀部署的结构1和结构2 能更有效地平衡整个网络节点的能量，延长网络的生存时间。

图6 剩余节点数随时间变化Fig 6 Numbers of remaining nodes change with time

3.4 网络能量消耗仿真分析

网络能量消耗从两方面进行分析，网络剩余能量反映了网络整体的能量消耗情况，节点能量消耗均匀性反映了网络能量消耗的均匀程度[12]。图7显示了本算法和结构1、结构2算法在网络生命期内节点的能量剩余情况，可看出本文算法剩余的能量明显大于结构1、结构2算法，说明网络的能源得到充分应用。图8显示了本文算法和结构1、结构2算法在网络生命期内节点的能量消耗均匀情况，可看出本文算法的节点剩余能量标准差远小于结构1、结构2算法，说明本文算法达到了设计时均衡网络能量消耗的目的，避免了由于单个节点的能量失效而影响网络性能的弊端。

4 结束语

本文介绍了水下节点部署的目标和约束条件，构建了UWSNs结构模型，并设计了一种能耗均衡的节点部署算

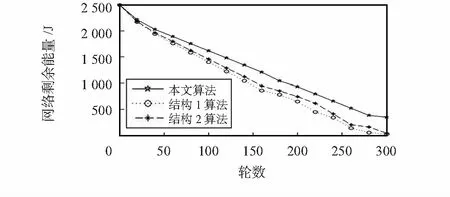
图7 网络剩余能量随时间变化Fig 7 Remaining energy of network change with time

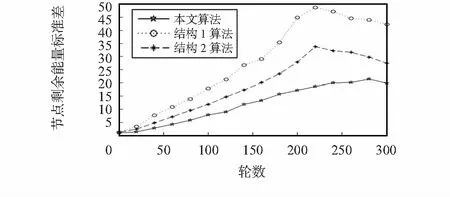
图8 网络能量消耗均匀程度随时间变化Fig 8 Uniformity of energy consumption change with time

法，同时，对算法从网络的生存时间和网络的能量消耗两方面进行了分析和仿真。仿真表明:本文算法所构建的网络能有效平衡网络能量，显著延长网络寿命。

[1]JimP,JimK,BrianNL.Asurveyofpracticalissuesinunder-waternetworks[J].ACMSIGMOBILEMobileComputingandCommunications,2007,11(4):23-33.

[2] 郭忠文,罗汉江,洪 锋,等.水下无线传感器网络的研究进展[J].计算机研究与发展,2010,47(3):377-389.

[3]ZhangHonghai,HouJenniferC.Maintainingsensingcoverageandconnectivityinlargesensornetworks[J].WirelessAdHocandSensorNetworks,2005,1(1):89-124.

[4]AkyildizIF,PompiliD,MelodiaT.Challengesforefficientcommunicationinunderwateracousticsensornetworks[J].ACMSigbedReview,2004,1(2):3-8.

[5] 李 龙,刘建明,李宏周,等.基于位置和能量的水下无线传感网路由协议[J].计算机应用研究,2014 (11):3429-3433.

[6] 刘建明,张存广,李宏周,等.移动传感器网络分层路由算法研究[J].桂林电子科技大学学报,2010,30(5):436-439.

[7] 刘华峰.传感器网络三维拓扑组织及分簇算法研究[D].长沙:国防科学技术大学,2007.

[8] 王 方,陈名松,罗 娜,等.水声传感器网络数据传输能耗分析[J].计算机系统应用,2011,20(4):91-95.

[9] 罗汉江.海洋监测传感器网络关键技术研究[D].青岛:中国海洋大学,2010.

[10] 刘丽萍.无线传感器网络节能覆盖[D].杭州:浙江大学,2006.

A three-dimensional deployment algorithm for underwater wireless sensor networks node*

ZHAO Min-hua1, LI Ling-yan1, ZHAO Kun1, LI Li2, KANG Yan-ni1

(1.School of Information and Control Engineering,Xi’an University of Architecture and Technology,Xi’an 710055,China;2.Northwest Institute for Design and Research,Xi’an 710082,China)

Starting from the requirements of water environment monitoring application,propose target and constraints of node deployment in 3D underwater space.And then,in order to solve imbalance energy consumption problems of nodes after sparse deployed in model of three-layer underwater wirless sensor networks(UWSNs),an inhomogeneous simple cubic lattice node deployment algorithm is proposed.This algorithm is designed by increasing the number of nodes of each layer and adjusting communication distance between nodes to control energy consumption of nodes combining energy consumption of underwater acoustic communication.The analysis and simulation on this algorithm from network lifetime and energy consumption is discussed,results show that the algorithm can not only guarantee the coverage requirements and control the density of nodes deployment,but also balance energy consumption of nodes and prolong the network lifetime.

underwater wireless sensor networks(UWSNs); deployment; simple cubic lattice; communication energy model; network lifetime

10.13873/J.1000—9787(2015)12—0138—04

2015—03—06

陕西省教育厅自然科学基金资助项目(12JK0999)；西安建筑科技大学科技计划基金资助项目(JC1215)

TP 393

: A

: 1000—9787(2015)12—0138—04

赵敏华(1971-)，女，陕西西安人，博士后，副教授,研究方向为无线传感器网络、建筑节能、工业控制。