基于混沌粒子群与蚁群算法的WSN路由协议

郑 波，崔宝同

（江南大学 物联网工程学院，江苏 无锡 214122）

无线传感器网络是将传感器技术、微机电系统技术、无线通信技术、分布式信息处理技术集成使用的一种网络[1]，能广泛的应用在军事、民用等各个领域。无线传感器网络与传统网络最大的区别是网络能量有限。因此，如何减少网络能量消耗，延长网络生存周期，就成为无线传感器网络的研究重点之一。采用分簇路由协议和多跳通信路由是如今比较常用的方式。

LEACH协议是最早提出的分簇协议[2]，该协议采用随机的簇头选择方式。节点成为簇头的条件是它所产生的随机数小于预设的阀值。LEACH协议的簇头选择是周期性进行的，为了延长网络的生命周期，高效地利用网络中所有的能量。LEACH协议最大的缺陷在于簇头选择过程中没有考虑节点剩余能量，而这会引起网络能量的消耗不均衡。而且簇头到基站，簇头到簇成员节点的通信都是采用单跳的方式，如果传输距离较远，就会使节点能量迅速耗尽。此后，很多学者在这两方面进行了研究改进。文献[3]首次将剩余能量作为簇头选择的一个依据，使剩余能量多的节点成为簇头的概率增加；文献[4]在此基础上进一步要求当选为簇头的节点剩余能量必须高于网络的平均能量。智能算法在解决簇头选择问题中有其独特的优势。文献[4]就在基站采用模拟退火算法来改进协议。通过对蚁群算法的研究发现，蚁群算法对路径寻优有着独特的优势。因此，本文首先用新的混沌粒子算法优化簇头选择，然后采用蚁群算法优化多跳路径，综合优化无线传感器网络的能量利用。

1 簇头选择机制

经典的分簇路由算法——LEACH算法，没有考虑节点的剩余能量和簇成员之间的紧密度。簇头在无线传感器网络中会承担更多的任务，如果被选为簇头的节点剩余能量少，能量就会很快耗尽，导致节点早亡。如果簇内节点通信距离较短即较为密集，则在数据传输过程中能量消耗就少。本文在考虑上述两个因素后提出基于节点剩余能量和簇间紧密度的适应度函数，适应度函数定义如式（1）。

其中，f1代表能量消耗，f2代表簇间距离，α1，α2是影响因素的权重，α1+α2=1，c 代表特定的群，E，E′分别代表能量消耗和剩余能量，|Cc|代表群c中的节点数目。

1.1 新的混沌粒子群算法

粒子群算法易陷入局部最优，因此可以利用混沌变量的遍历性，解决因为粒子停滞导致的算法早熟问题。

基本的粒子群算法的描述如下：

设搜索空间为D维，种群数为m，第i个粒子（i=1，2，…，m）的位置表示为 Zi=（zi1，zi2，ziD），Vi=（vi1，vi2，viD）为粒子 i的位置移动距离，Pi=（pi1，pi2，…，piD）表示第 i个粒子“飞行”历史中最优位置，Pg=（pg1，pg2，…，pgD）表示整个种群历史最优位置，t表示迭代次数。粒子根据以下公式更新速度和位置：

c1，c2为学习因子，其值高低对收敛速度有一定影响，但不大，一般取（0，2）之间的随机值。 rand（）是[0，1]之间的随机数。ω是惯性权重，起着权衡局部最优能力和全局最优能力的作用。当惯性权值较小时，算法的收敛速度很快，但是容易陷入局部最优；当惯性权值较大时，虽然不会陷入局部最优，但收敛速度很慢。所以一般采用公式（6）的惯性权重函数，使惯性权值随线性减少。

其中，ωmax为初始权重；ωmin为最终权重；tmax为最大迭代次数；t为当前迭代次数。

本文采用文献[5]的混沌粒子群算法，该算法是将混沌融入到粒子群过程中，能产生优于其他混沌粒子群优化算法的结果。

本文的簇头选择算法模型如下式[5]：

其中式（7）是用来更新粒子的速度公式。式（8）是混沌变量，对粒子的混沌程度产生影响。当cid（t）→0时，依旧采用粒子群算法进行位置更新，当cid（t）→1时，主要是粒子群个体的混沌在起作用。rid表示第i个粒子的第d维的混沌因子，是一个大于0.5小于1的值。式（9）是将混沌引入到粒子位置更新中。ψd定义为搜索测度。

根据文献[6]的结论映射不依赖初始值位置，且比logistic或Tent映射的平均搜索效率分别提高了71.6%和62.6%。因此，文中采用Fuch映射，公式如（10）所示。

对于寻优而言，系统一直处于稳定或者混沌状态都是不利的，只有在混沌与稳定之间相互交替才能寻找到最优值。就是在稳定时引入混沌，帮助粒子跳出局部最优；在不稳定时，加速向最优值靠近，加快收敛速度。通过下述两个式子来判断粒子所处的状态：

当m<10-6且s<10-6且k<0.9tmax时，粒子处于稳定状态，此时引入混沌，令 cid（t）=0.99；当 s>10-6且 k<0.9tmax时，粒子不稳定，为了加快收敛速度，令 Zid（t）=Pid（t）。

1.2 基于新的混沌算法的簇头选择

产生簇头步骤：

假设初始的无线传感器网络，节点带有相同的初始能量，第一轮采用LEACH算法的簇头选举机制。

第一轮簇头选择与LEACH算法相同，簇头选举出来后，采用蚁群算法计算簇头到基站的多跳路径。经过一轮运行以后各个节点的剩余能量产生了变化，不再相等了，第二轮以后采用混沌粒子群优化算法选举簇头。

基于混沌粒子群优化算法的簇头选举步骤：

1）初始化N个粒子，每个粒子代表一种分簇可能；

2）通过适应度函数计算粒子适应值，记录全局最优解和粒子历史最优解；

3）通过新的混沌粒子群算法更新粒子，并记录个体最优解和全局最优解；

4）重复步骤 2）、3），直到最大迭代次数；

5）发布簇头信息。

簇头确定后向非簇头节点发布广播，非簇头节点根据接收信号的强度选择强度最大的簇头，发送加入请求。

2 基于蚁群算法的多跳路由

与数据融合、计算等相比，无线传感器网络的主要能耗是发生在通信过程中，因此要节约网络能量，就要改进通信方式，采用高效率的路由。在LEACH协议中，簇头与其他节点包括基站通信，都是采用单跳通信的方式。因为簇头到基站的距离往往比较远，距离较远的数据传输采用多径衰落模型，会使簇头能量快速耗尽，因此通过寻优方法来改进簇头到基站的路由。

2.1 基于蚁群优化的多跳路由

蚁群算法只是单纯的寻找从源到目的的最短路径，在该路径上蚂蚁的数量将是最大的，这会导致这条路径上的能量消耗最大，然而蚂蚁在选择下一跳时没有考虑节点剩余能量。蚂蚁运行可能会偏离基站。本文采用文献[7]中采用的基于蚁群优化的LEACH路由协议。

位于簇头i的蚂蚁k选择下一跳的簇头j的概率为：

Ej-current是簇头j的剩余能量，重新定义为允许蚂蚁k访问的下一跳簇头的集合。在文献[7]中没有对能量对比的参数进行明确定义，本文中，Ep-current为当前无线传感器网络节点平均能量。通过该设定使节点在选择下一跳是能够选择能量较多的节点。设定的规则是簇头j在簇头i的通信半径内，簇头j还没被蚂蚁k访问过，簇头j到基站的距离小于簇头i到基站的距离。该设定规则是为了防止蚂蚁k朝偏离基站的方向运行。ηij重新定义为：

ηij这样定义是为了考虑传输路径上的能耗。使离簇头i近的簇头有更大的机会成为下一跳簇头。从（13）和（14）式中可以看出簇头j的剩余能量越多，离簇头i越近，被选为下一跳的概率就越大。

每一个簇头上蚂蚁按照下面的伪随机码规则决定下一跳选择哪个簇头：

q是一个服从[0，1]均匀分布的随机数，q≤q0时按照先验知识选择路径，否则就是按照一定的概率（t）选择路径。 q0是一个常数，可以通过设定q0的大小来使蚂蚁以一定的概率开辟新路径，防止陷入局部最优。l是一个服从蚁群算法的概率选择的随机数。

全局信息素更新：采用ASC信息素规则，信息素的挥发或释放只在最优边上进行。全局更新是在所有蚂蚁完成它们路径后执行使用下式对所建立的路径进行更新：

其中，Lb为最优路径的总长度。

局部信息素更新公式如下：

τ0为初始信息素浓度，ξ为局部每条边上信息素蒸发率。在寻找最优路径过程中，蚂蚁每经过一条边就运用式（17）更新这条边上的信息素浓度。

假设基站为蚂蚁的食物目的地，蚂蚁从所在的簇头开始寻找食物。蚂蚁k到达基站后停止本次搜索，基站为终点。

1）初始化。设置最大迭代次数Nmax，计算簇头间的距离dij，并用距离远近排序；

2）将m个蚂蚁均匀的放在簇头，蚂蚁是同构的。每个蚂蚁携带出发簇头的ID，所经过的中间簇头的ID和剩余能量，中间簇头间的距离。蚂蚁开始循环；

（4）按照式（15）选择下一跳簇头 j；

5）蚂蚁访问过一个簇头后就按式（17）立即更新该路径上的信息素；

6）当 m只蚂蚁都达到基站后，计算最优的 Lb，Lb=Σdij，用式（16）对最优的蚂蚁路径上进行信息素更新，使蚂蚁主要集中在当前已找到的最优路径领域内；

7）如果没有停滞，或没达到最大迭代次数就返回步骤2）；停滞是指在迭代范围内3次搜索到相同的值；

8）输出最优值。

3 系统模型

3.1 网络模型

本文采用分层次网络拓扑结构。网络由簇成员节点、簇头节点和基站组成。分簇算法将网络节点分成多个簇。每个簇有一个簇头节点和若干簇成员节点组成，簇成员节点将采集到的数据传给簇头节点，簇头节点将自身采集到的信息与接收到的簇成员节点采集到的信息经过数据融合再传给基站。基站能量不受限，拥有较强的处理能力、存储能力和通信能力，起到连接无线传感器网络和外部网络的作用。在本文中假设节点所携带的能量是有限的且能感知节点的剩余能量，有GPS定位功能能获取自己相对基站的位置信息。

3.2 能耗模型

节点的主要能量消耗是产生在信息收发和处理过程，其他的能量消耗与之相比可忽略不计。本文所采用的能耗模型是由Heinzelman等在信道能量损耗模型基础上提出的改进模型[8]。

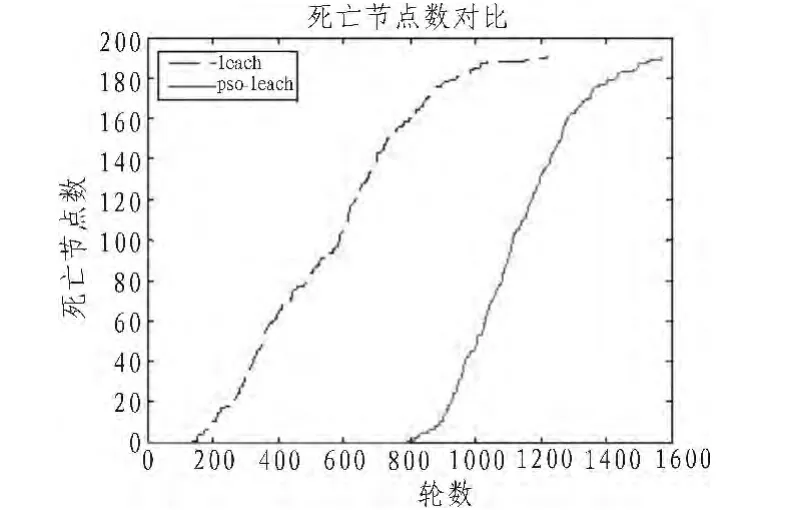
该模型考虑了不同传输距离时无线信号对数据传输的影响，根据信号强度的衰落与传输距离的远近分成了自由空间信道模型和多径衰落信道模型。设定一个阀值d0，当传输距离d

接收节点消耗的能量为：

其中，Eelec是发送电路和接收电路的能量消耗；εfs和εmp分别是自由空间模型和多径衰减模型中功率放大器的能量消耗；阀值

4 仿真分析

将本文算法在无线传感器网络中的性能进行matlab仿真，并与LEACH协议在相同条件下进行比较。参数设置如表1所示。

混沌粒子群优化算法的各参数为：初始化粒子数为20，c1=c2=2，ωmax=0.9，ωmin=0.4，α1=0.6，α2=0.4，ψd=200，rid=0.5+（0.005）rand。

蚁群算法约束参数设置为：α=0.1，β=3，ρ=0.1，m=K。

取200 m×200 m的区域，随机部署200个节点，选用网络生命周期和能耗两个技术指标来评价算法的性能。

仿真图1显示了本文的协议与LEACH协议整个网络总能耗的对比。纵轴代表网络的总能量，横轴代表仿真的时间。可见，从整个网络能耗来看，本文的协议大大节省了能量消耗，延长了近400轮的网络生存时间。而且由斜率来看，本文的协议能量消耗比较均衡。

表1 参数设置Tab.1 Parameters

图1 能耗对比Fig.1 The energy consumption contrast

下面的图2显示了本文的协议与LEACH协议网络生存周期的对比。从图2中可以看出，LEACH协议第一个死亡节点出现在119轮，本文的协议的第一个死亡节点出现在800轮，延长了572%。一半节点的死亡，LEACH协议发生在540轮左右，本文的协议则在1 120轮左右，到1 110轮，LEACH协议节点基本已经死亡，而本文的协议则到了1 580轮。一半节点死亡时间延长了106.8%，网络生存周期延长了41.99%，可以明显看出延长了网络寿命。

图2 网络生存周期对比Fig.2 The network lifetime comparison

5 结 论

本文提出了一种基于混沌粒子群和蚁群相结合的路由协议。利用混沌粒子群算法在簇头选择中的优势，结合对节点剩余能量和簇的紧密性的考虑，改进了簇头选举策略。同时利用蚁群算法的寻优能力，优化多跳路由。两种方法的结合有效的延长了网络生命周期。下一步的研究主要针对智能算法优化多跳路径。

[1]彭力.无线传感器网络技术 [M].北京:冶金工业出版社，2011.

[2]Heinzelman W，Chandrakasan A，Balakrishnan H.Energyefficient communication protocol for wireless microsensor netwo-rks[C]//Proc.of the 33rd Annual Hawaii Internatioal Conf.on System Younis Scie-nces.Maui:IEEE Computer Society，2000:3005-3014.

[3]Handy M J，Haase M，Timmerrnann M D.Low energy adaptive clustering hiera-rchy with deterministic cluster-head sel-ection[C]//Proc.of the 4th IEEE Conf.on Mobile and Wireless Communications Ne-tworks.Stockholm:IEEE Communications Society，2002:368－372.

[4]Heinzelman W，Chandrakasan A，Balakr-ishnan H.An application-specific protocol architecture for wireless microsensor ne-tworks[J].IEEE Trans on Wireless Comm-unications，2002，1（4）:660－670.

[5]胥小波，郑康锋，李丹，等.新的混沌粒子群优化算法[J].通信学报，2012，33（1）:24-37.XU Xiao-bo，ZHENG Kang-feng，LI Dan，et al.New chaosparticle swarm optimization algorithm[J].Journal on Communications，2012，33（1）:24-37.

[6]傅文渊，凌朝东.自适应折叠混沌优化算法[J].西安交通大学学报，2013，47（2）:33-38.FU Wen-yuan，LING Chao-dong.An adaptive lterative chaos optimization method[J].Journal of Xi’An Jiaotong University，2013，47（2）:33-38.

[7]吴丽君.无线传感器网络LEACH协议的研究与改进[D].上海：华东理工大学，2010.

[8]Heunzelman W B，Chandrakasan A P，Balakrishnan.An application-specific protocol architecture for Wireless Microsensor Networks[J].IEEE Trans on Wireless Communications，2002，1（4）:660-670.